Problem 1

The splitting field of this polynomial is \({\mathbf{Q}}(\sqrt[3]2, \sqrt 3, \zeta_3)\) where \(\zeta_3\) is a primitive third root of unity.

To get the degree of this extension, we extend fields in the indicated order. Since \({\mathbf{Q}}(\sqrt[3] 2, \sqrt 3)\) is totally real, the minimal polynomial of \(\zeta\) over it still has degree \(\phi(3) = 2\). A quick check also shows that \(\sqrt 3\) is not contained in \({\mathbf{Q}}(\sqrt[3] 2)\), yielding another degree 2 extension, and finally a degree 3 extension.

Thus we have an extension of degree 12, and since we’ve constructed a Galois extension \(L\) (a separable splitting field), if we define \(G \coloneqq{ \mathsf{Gal}}({\mathbf{Q}}/L)\), we have \({\left\lvert {G} \right\rvert} = 12\). Since we know that the splitting field of \({\mathbf{Q}}(\sqrt[3] 2)/ {\mathbf{Q}}\) has Galois group \(D_3\), we must have \(D_3 \leq G\). This reduces the possibilities just \(D_3 \times{\mathbf{Z}}_2 \cong D_6\).

We have the following subgroup diagram (Figure 1).

\

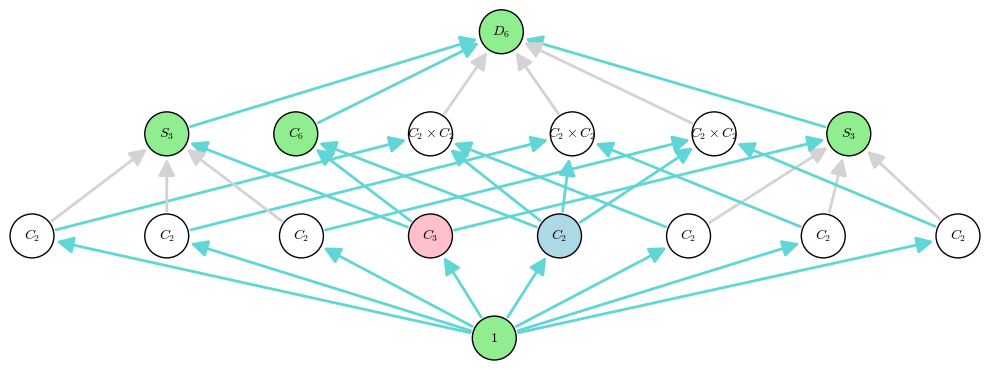where we can simplify things by only considering conjugacy classes of subgroups, since these will correspond to conjugate field extensions (Figure 2).

\

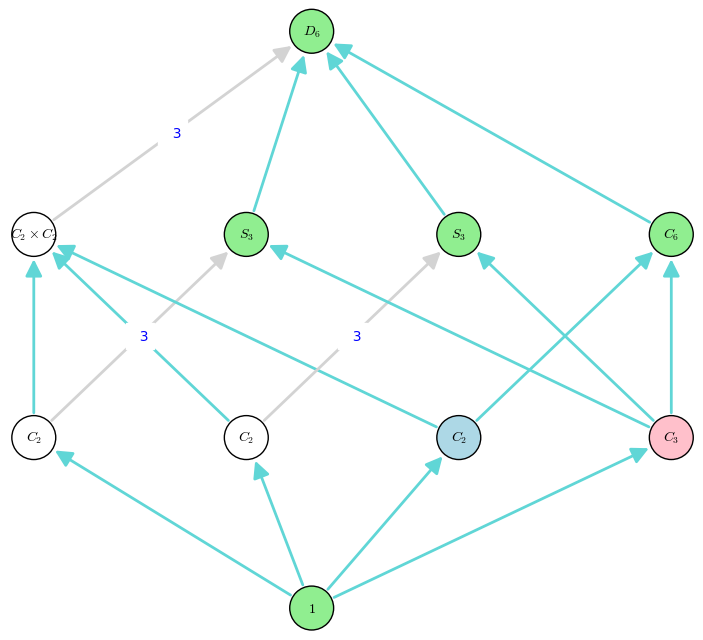We can explicitly identify the relevant automorphisms: \begin{align*} \begin{align*} \sigma: \sqrt[3] 2 \mapsto \zeta_3 \sqrt[3] 2 \\ \tau: \zeta_3 \mapsto \zeta_3^2 \\ \gamma: \sqrt 3 \mapsto -\sqrt 3 .\end{align*} \end{align*} We can then present \(G = \left\langle{\sigma, \gamma, \tau \mathrel{\Big|}\sigma^3 = \tau^2 = \gamma^2 = (\sigma\tau)^2 = [\sigma, \gamma] = [\tau, \gamma] = e}\right\rangle\), and obtain the following lattice:

\begin{align*} \begin{tikzcd} & & {<\sigma, \tau, \gamma>} & & & & \\ & & & & & & \\ <\tau> \times <\gamma> \arrow[rruu, dashed] & & {<\sigma, \tau>} \arrow[uu] & & {<\sigma, \tau\gamma>} \arrow[lluu] & & <\sigma> \times <\gamma> \arrow[lllluu] \\ & & & & & & \\ <\tau> \arrow[uu] \arrow[rruu, dashed] & & <\tau\gamma> \arrow[rruu, dashed] \arrow[lluu] & & <\gamma> \arrow[rruu] \arrow[lllluu] & & <\sigma> \arrow[uu] \arrow[lluu] \arrow[lllluu] \\ & & & & & & \\ & & & \arrow[llluu] \arrow[luu] \arrow[ruu] \arrow[rrruu] & & & \end{tikzcd} \end{align*}

which, up to conjugacy, fix the following intermediate field extensions (Figure 3).

\

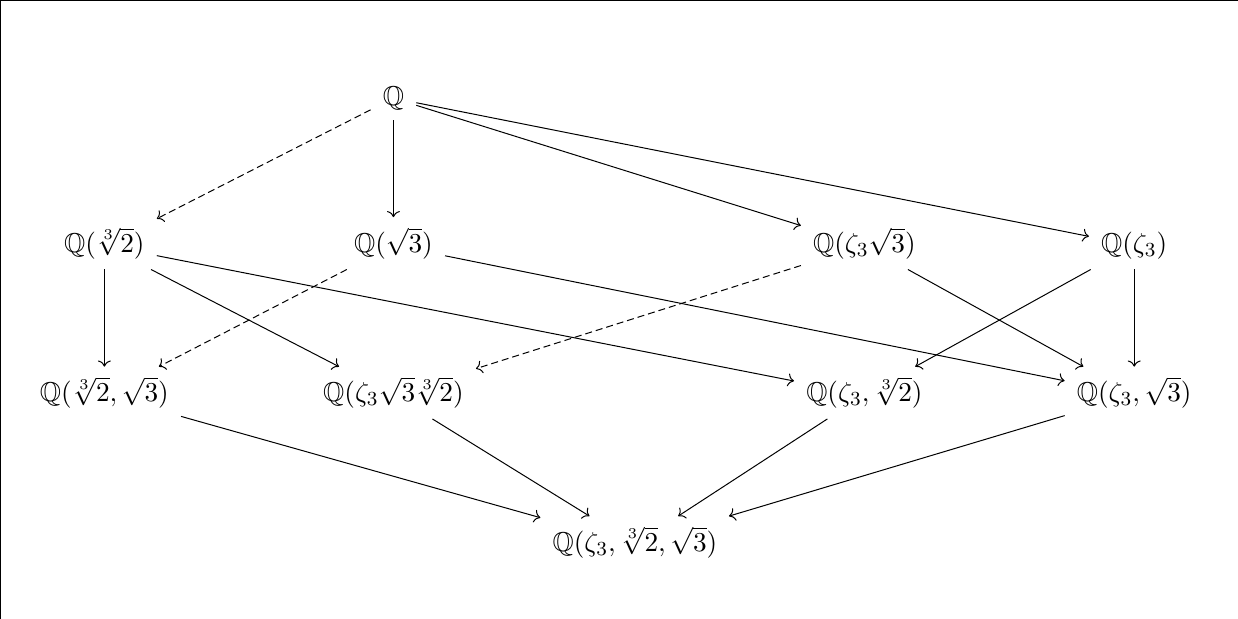\(\hfill\blacksquare\)

Problem 2

We can note that since \(f\) has 4 roots, the Galois group \(G\) of its splitting field will be a subgroup of \(S_4\). Moreover, \(G\) must be a transitive subgroup of \(S_4\), i.e. the action of \(G\) on the roots of \(f\) should be transitive. This reduces the possibilities to \(G \cong S^4, A^4, D^4, {\mathbf{Z}}_4, {\mathbf{Z}}_2^2\).

Since \(f\) has exactly 2 real roots and thus a pair of roots that are complex conjugates, the automorphism given by complex conjugation is an element of \(G\). But this corresponds to a 2-cycle \(\tau = (ab)\), and we can then make the following conclusions:

• Not \(A_4\): \(A_4\) contains only even cycles, and \(\tau\) is odd.
• Not \(Z_4\): This subgroup is generated by a single 4-cycle \(\sigma\), which up to conjugacy is \((1234)\), and \(\sigma^n\) is not a 2-cycle for any \(n\).
• Not \({\mathbf{Z}}_2^2\): In order to be transitive, this subgroup must be \(\left\{{e, (12)(34), (13)(24), (14)(23)}\right\}\), which does not contain \(\tau\).

The only remaining possibilities are \(S^4\) and \(D^4\). \(\hfill\blacksquare\)

Problem 3

Part 1

To see that \(\phi(n)\) is even for all \(n>2\), we can take a prime factorization of \(n\) and write \begin{align*} \phi(n) = \phi\left( \prod_{i=1}^m p_i^{k_i}\right) = \prod_{i=1}^m \phi(p_i^{k_i}) = \prod_{i=1}^m p^{k_i - 1}(p - 1) = \prod_{i=1}^m p^{k_i - 1} \prod_{i=1}^m (p - 1) \end{align*}

where each \(k_i \geq 1 \implies k_i-1 \geq 0\). But every prime power is odd, and a product of odd numbers is odd, so the first product is odd. It is also true that \(p-1\) is even for every prime \(p\), and the second term is a product of even terms and thus even. So \(\phi(n)\) is the product of an even and an odd number, which is always even.

Part 2

Suppose \(\phi(n) = 2\). Take a prime factorization of \(n\), so we have \begin{align*} 2 = \phi(n) = \prod_{i=1}^m \phi(p_i^{k_i}) \end{align*}

Since the only factors of 2 are 1 and 2, we must have \(\phi(p_i^{k_i}) = 2\) for exactly one \(i\), and the rest must be equal to 1.

Consider the term that equals 2. We have \(\phi(p_i^{k_i}) = p^{k_i - 1}(p-1) = 2\), so we must have either

• Case 1: \(p-1 = 2\) and \(p^{k_i - 1} = 1\), so \(p=3\) and \(k_i = 1\). So \(3 \divides n\), but \(3^\ell\) does not divide \(n\) for any \(\ell > 1\).
• Case 2: \(p^{k_i - 1} = 2\) and \((p-1) = 1\), so \(p=2\) and \(k_i = 2\). Thus \(2^2\) divides \(n\) but \(2^\ell\) does not for any \(\ell > 2\).

In either case, it remains to check are whether the other factors where \(\phi(p_j^{k_j}) = 1\) can contribute any other distinct divisors to \(n\). We can note that \(\phi(p_j^{k_j}) = 1\) iff \(p^{k_j-1}(p-1) = 1\), so this forces \(p=2\) and \(k_j = 1\). So \(n\) may or may not contain a single factor of 2, but by uniqueness of prime factorization, this can only happen in case 1. Note that this also forces \(2\divides n\) but \(2^2\) does not divide \(n\).

In summary, we’ve found that \(\phi(n) = 2\) implies that

• \(3 \divides n\), 9 does not divide \(n\), and
  • \(2\divides n\), 4 does not divide \(n\)
  • \(2\) does not divide \(n\)
• \(2^2 \divides n, 2^3\) does not divide n.

This reduces the possibilities to the finite set \(n \in \left\{{6,3,4}\right\}\), and \(\phi(6) = \phi(3) = \phi(4) = 2\). \(\hfill\blacksquare\)

Problem 4

Note that since \(\zeta(\zeta+\zeta^{-1}) = \zeta^2 + 1\), we have the relation \(\zeta^2 - (\zeta+\zeta^{-1})\zeta + 1 = 0\). But then \begin{align*} f(x) = x^2 - (\zeta + \zeta^{-1})x + 1 \end{align*}

is a polynomial in \({\mathbf{Q}}(\zeta + \zeta^{-1})\) for which \(f(\zeta) = 0\). Thus \(g = \min(\zeta, {\mathbf{Q}}(\zeta + \zeta^{-1}))\) divides \(f\), but since \(\deg f = 2\) and \({\mathbf{Q}}(\zeta + \zeta^{-1})\) is totally real, \(\zeta\not\in{\mathbf{Q}}(\zeta + \zeta^{-1})\). This means that \(g\) can not be linear and must have degree at least 2, but the above argument shows that \(g\) has degree at most 2, so it must be 2. Letting \(m = [{\mathbf{Q}}(\zeta + \zeta^{-1}): {\mathbf{Q}}]\), we have \begin{align*} \begin{align*} [{\mathbf{Q}}(\zeta) : {\mathbf{Q}}] &= [{\mathbf{Q}}(\zeta): {\mathbf{Q}}(\zeta + \zeta^{-1})] [{\mathbf{Q}}(\zeta + \zeta^{-1}) : {\mathbf{Q}}] \\ \implies \phi(n) &= 2 m ,\end{align*} \end{align*}

and so \(m = \phi(n)/2\) as desired.

Problem 5

Suppose \(F = K[\alpha_1, \cdots, \alpha_n]\) where \(\alpha_1^{n_1} \in K\) for some \(n_1\) and }or each \(i\) we have \(\alpha_i^{n_i} \in K[\alpha_1, \cdots, \alpha_{i-1}]\) for some powers \(n_i\). We want to show that \(F = E[\beta_1, \cdots \beta_m]\) where each \(\beta_i\) satisfy a similar condition.

Let \(A = \left\{{\alpha_i {~\mathrel{\Big\vert}~}\alpha_i \not\in E}\right\}\), then it is since \(E \hookrightarrow F\), adjoining all elements of \(A\) to \(E\) will yield exactly \(F\). Using the order of \(\alpha_i\) given by the definition of \(F\) as a radical extension, let \(\beta_1\) be the \(\alpha_i \in A\) with the smallest index \(i\). Then by assumption, there is some \(m_1\) such that \(\beta^{m_1} \in K[\alpha_1, \cdots, \alpha_{i-1}] \subset F\), so we can construct \(F_1 \coloneqq E[\beta_1]\) which will be a radical extension.

Inductively letting \(A_2 = A \setminus\left\{{\beta_1}\right\}\) and repeating this process to construct \(L_2\) will yield radical extensions at every step, and since \(A\) is finite, there is some \(n\) such that \(L_n = L\). But then \(L\) is a radical extension over \(E\) as desired.

Problem 6

Part 1

Since \(f\) is irreducible of degree \(n\) and \(u\) is a root of \(f\), the minimal polynomial of \(u\) over \(K\) is in fact \(f\), and thus the degree of the extension \(K(u) / K\) is given by

\begin{align*} [K(u) : K] = \deg \min(u, K) = n. \end{align*}

To see that \(K(u)\) is not Galois, we just note that since \(f\) was irreducible, and \(u\) was only one root of \(f\), \(K(u)\) is not the splitting field of \(f\), and is thus not the splitting field of any other irreducible polynomial over \(K\).

To see that \(\mathrm{Aut}(K(u)/ K)\) is trivial, note that any \(K{\hbox{-}}\)automorphism of \(K(u)\) can only send \(u\) to one of its conjugates. But the only conjugate of \(u\) in \(K(u)\) is \(u\) itself, so only the identity automorphism can occur.

Part 2

The normal closure \(L\) of \(K\) is defined as the smallest extension of \(K\) such that if \(\alpha\) is a root of any irreducible polynomial in \(K[x]\) and \(\alpha \in L\), then all of its conjugates are in \(L\) as well. But this means any such polynomial splits in \(L\). In particular, if \(u\in L\), then \(f\) splits in \(L\), and so \(L\) contains the splitting field \(F\).

Part 3

By a theorem in class, this would force \({ \mathsf{Gal}}(E/K)\) to be solvable, which would imply that \(S_n\) is solvable – but for \(n\geq 5, S_n\) will not be solvable, a contradiction.

Qual Problems

Problem 1

Part 1

If \(L/K\) is a finite field extension which is both separable and a splitting field of some polynomial in \(K[x]\), then \([L: K] = {\left\lvert {{ \mathsf{Gal}}} \right\rvert}{L/ K}\).

Part 2

The extension \({\mathbf{Q}}(\zeta_{43})\) is the splitting field of the cyclotomic polynomial \(\Phi_{43}(x) = \sum_{i=1}^42 x^i\), which is degree \(\phi(43) = 42\) since \(43\) is prime.

Moreover, the Galois group is isomorphic to \({\mathbf{Z}}_{43}^{\times}\cong {\mathbf{Z}}_{42}\).

Part 3

Since proper subfields will correspond to intermediate extensions which will correspond to subgroups of the Galois group, this problem is reduced to counting the number of distinct subgroups of \({\mathbf{Z}}_{42}\). This is a cyclic group, so there is exactly one subgroup of order \(d\) for each \(d\) dividing 42. Since \(42 = 2*3*7\), we have

• A subgroup of order 2, corresponding to a field extension of degree 21,
• A subgroup of order 3, corresponding to a field extension of degree 14,
• A subgroup of order 6, corresponding to a field extension of degree 7,
• A subgroup of order 7, corresponding to a field extension of degree 6,
• A subgroup of order 14, corresponding to a field extension of degree 3,
• A subgroup of order 21, corresponding to a field extension of degree 2.

Problem 2

Part 1

A splitting field of \(f\) over \(F\) is an extension \(L \geq F\) that contains every root of \(f\), so that \(f\) can be decomposed as a product of linear factors i.e. \(f(x) = \prod_{i=1}^{\deg f} (x-\alpha_i)^{m_i}\) in \(L[x]\).

Part 2

If \(E \geq F\) is a finite extension, then it is algebraic and \(E = F[\alpha_1, \cdots, \alpha_n]\). So we can let \(g(x) = \prod_{i=1}^n (x-\alpha_i)\). By construction, each \(\alpha_i\) is a root, and so \(E\) is a splitting field for \(g\).

Part 3

Since \(E\) was shown to be a splitting field, it only remains to show that it is separable. But this follows from the fact that each \(\alpha_i\) is a separable element, since their minimal polynomial over \(F\) is \(g\). So \(E\) is a Galois extension.

Problem 3

Part 1

False: take \(K \leq L \leq M\) as \({\mathbf{Q}}\leq {\mathbf{Q}}(\sqrt[3]2) \leq {\mathbf{Q}}(\sqrt[3]2, \zeta_3)\). Then \(M\) is the splitting field of \(x_3-2\), and in characteristic zero is thus Galois. But \(L\) is not the splitting field of any irreducible polynomial in \({\mathbf{Q}}[x]\), so it is not Galois.

Part 2

This is true. By the Galois correspondence, it suffices to show that \(H \coloneqq{ \mathsf{Gal}}(M/L)\) is a normal subgroup of \(G \coloneqq{ \mathsf{Gal}}(M/ K)\). To that end, let \(\phi \in G\), so \(\phi: M \to M\) is a lift of \(\operatorname{id}_K\). Then \(H {~\trianglelefteq~}G\) iff \(\phi H \phi^{-1}= H\). Letting \(\sigma \in H\), we need to show that \begin{align*} (\phi^{-1}\circ \sigma \circ \phi)(L) = L, \end{align*} i.e. that this composition is some automorphism of \(M\) that fixes \(L\).

Consider how this acts on elements of \(L\). If \(\ell \in L\), then \(\ell = \sum k_i \ell_i\) since \(L\) is a finite-degree extension, thus algebraic, thus spanned by some basis \(\ell_i \in L\) as a vector space over \(K\).

In particular, since \(\phi\) is some \(M{\hbox{-}}\)automorphism, it restricts to an \(L{\hbox{-}}\)automorphism, which must send each \(\ell_i\) to some conjugate \(\ell_i'\). Similarly, \(\phi^{-1}(\ell_i') = \ell_i\).

We thus have \begin{align*} \begin{align*} (\phi^{-1}\sigma \phi)(a) &= (\phi^{-1}\sigma \phi)(\sum k_i \ell_i) \\ &= (\phi^{-1}\sigma)(\sum k_i \phi(\ell_i)) \\ &= (\phi^{-1}\sigma)(\sum k_i \ell_i') \\ &= (\phi^{-1})(\sum k_i \sigma(\ell_i')) \\ &= (\phi^{-1})(\sum k_i \ell_i') \quad\text{since $\sigma$ fixes $L$}\\ &= \sum k_i \phi^{-1}(\ell_i') \\ &= \sum k_i \ell_i \\ ,\end{align*} \end{align*}

and so this composite fixes \(L\) as desired. This \(H {~\trianglelefteq~}G\), which is what we wanted to show.