Galois Theory

• Reduce to a group theory problem: \([E:F] = [G:H]\), despite the fact that \(E/F\) is not necessarily Galois. This is because we can count in towers: \begin{align*} [K:F] = [K:E][E:F] &\implies [G:1] = [K:E][H:1] \\ &\implies {\sharp}G = [K:E] {\sharp}H \\ &\implies [G:H] = {{\sharp}G \over {\sharp}H} = [K:E] .\end{align*}

• Essential fact: if \(P \in {\operatorname{Syl}}_p(G)\), we can use that \(P \subseteq N_G(P) \subset H\) and so \(P\in {\operatorname{Syl}}_p(H)\) as well.

• Now use that \(N_G(P) \subseteq H\), and do Sylow theory for \(P\) in both \(G\) and \(H\):

  • Sylow 3 on \(G\) yields \(n_p(G) = [G: N_G(P)] \equiv 1 \operatorname{mod}p\).
  • Sylow 3 on \(H\) yields \(n_p(H) = [G: N_H(P)] \equiv 1 \operatorname{mod}p\).

• Claim: \(N_H(P) = N_G(P)\).

  • We have \(N_H(P) \subseteq N_G(P)\) since \(H \subseteq G\), so \(hPh^{-1}= P\) remains true regarding either \(h\in H\) or \(h\in G\).
  • For \(N_G(P) \subseteq N_H(P)\), use that \(N_G(P) \subseteq H\) and so \(gPg^{-1}= P\) implies \(g\in H\), so \(g\in N_H(P)\).

• Now morally one might want to apply an isomorphism theorem: \begin{align*} {G/ N_G(P) \over H/N_H(P)}= {G/ N_H(P) \over H/N_H(P)}\cong {G\over H} ,\end{align*} but we don’t have normality. However, we can still get away with the corresponding counting argument if everything is finite: \begin{align*} {[G: N_G(P)] \over [H:N_H(P)] }= {[G: N_H(P)] \over [H:N_H(P)] }= {{\sharp}G / {\sharp}N_H(P) \over {\sharp}H / {\sharp}N_H(P)} = {{\sharp}G \over {\sharp}H} = [G: H] .\end{align*}

• We have an equation of the form \(n_p(G)/n_p(H) = m\), and we want to show \(m\equiv 1 \operatorname{mod}p\). So write \begin{align*} {n_p(G) \over n_p(H) } = m \implies m n_p(H) &= n_p(G) \\ \implies m n_p(H) &\equiv n_p(G) \operatorname{mod}p \\ \implies m\cdot 1 &\equiv 1 \operatorname{mod}p \\ \implies m &\equiv 1 \operatorname{mod}p .\end{align*}

• Some notation: let \(\alpha_k \coloneqq\zeta_n^k + \zeta_n^{-k}\).

• Let \(m(x)\) be the minimal polynomial of \(\alpha_1 \coloneqq\zeta_n + \zeta_n^{-1}\). Note that \(\alpha_1 \in {\mathbf{Q}}(\zeta_n)\).

• Use that \({ \mathsf{Gal}}({\mathbf{Q}}(\zeta_n)/{\mathbf{Q}}) \cong C_n^{\times}\), consisting of maps \(\sigma_k: \zeta \mapsto \zeta^k\) for \(\gcd(k, n) = 1\), of which there are \(\phi(n)\) many.

• Galois transitively permutes the roots of irreducible polynomials, so the roots of \(m\) are precisely the Galois conjugates of \(\alpha\), i.e. the Galois orbit of \(\alpha\), so we can just compute it. For illustrative purposes, suppose \(n\) is prime, then \begin{align*} \sigma_1(\zeta_n + \zeta_n^{-1}) &= \zeta_n + \zeta_n^{-1}=\alpha_1 \\ \sigma_2(\zeta_n + \zeta_n^{-1}) &= \zeta_n^2 + \zeta_n^{-2} = \alpha_2 \\ \sigma_3(\zeta_n + \zeta_n^{-1}) &= \zeta_n^3 + \zeta_n^{-3} = \alpha_3 \\ \vdots&\\ \sigma_{n-1}(\zeta_n + \zeta_n^{-1}) &= \zeta_n^{n-1} + \zeta_n^{-(n-1)} = \zeta_n^{-1} + \zeta_n^{1} = \alpha_1 \\ \sigma_{n-2}(\zeta_n + \zeta_n^{-1}) &= \zeta_n^{n-2} + \zeta_n^{-(n-2)} = \zeta_n^{-2} + \zeta_n^{2} = \alpha_2 \\ \sigma_{n-3}(\zeta_n + \zeta_n^{-1}) &= \zeta_n^{n-3} + \zeta_n^{-(n-3)} = \zeta_n^{-3} + \zeta_n^{3} = \alpha_3 ,\end{align*} where we’ve used that \(\zeta^{k} = \zeta^{k\operatorname{mod}n}\). From this, we see that \(\sigma_{k}(\alpha_1)=\sigma_{n-k}(\alpha_1)\) and we pick up \((n-1)/2\) distinct conjugates.

• For \(n\) not prime, the exact same argument runs through \(\phi(n)\) values of \(k\) for \(\sigma_k\), and again yields \(\sigma_{k}(\alpha_1) = \sigma_{\phi(n) - k}(\alpha_1)\). Matching them up appropriately yields \(\phi(n)/2\) distinct roots.

The setup:

Link to Diagram

Part 1:

• \(L/K\) is cyclic means \(L/K\) is Galois and \(G\coloneqq{ \mathsf{Gal}}(L/K) = C_n\) for some \(n\).
• By the FTGT, setting \(H \coloneqq{ \mathsf{Gal}}(L/E)\), we get \(H {~\trianglelefteq~}G\) precisely because \(E/K\) is normal, and \({ \mathsf{Gal}}(L/E) = G/H\).
• But then if \(G\) is cyclic, \(H \leq G\) must be cyclic, and \(G/H\) is cyclic as well since writing \(G = C_n = \left\langle{x}\right\rangle\), we have \(G/H = \left\langle{xH}\right\rangle\).

Part 2:

• Letting \(G\coloneqq{ \mathsf{Gal}}(L/K) = C_n\), by elementary group theory we have subgroups \(H\coloneqq C_d \leq C_n\) for every \(d\) dividing \(n\).
  • A observation we’ll need: every subgroup is normal here since \(G\) is abelian.
• By the fundamental theorem, taking the fixed field of \(H \leq { \mathsf{Gal}}(L/K)\), we obtain some intermediate extension \(E\coloneqq K^H\) fitting into a tower \(L/E/K\).
• By the fundamental theorem, \([E: K] = [G:H] = n/d\), where we’ve used that \(H{~\trianglelefteq~}G\).
• Letting \(d\) range through divisors lets \(n/d\) range through divisors, so we get extensions of every degree \(d\) dividing \(n\).

• \(L/k\) is separable iff every element \(\alpha\) is separable, i.e. the minimal polynomial \(m(x)\) of \(\alpha\) is a separable polynomial, i.e. \(m(x)\) has no repeated roots in (say) the algebraic closure of \(L\) (or just any splitting field of \(m\)).

• If \(\operatorname{ch}k = p\), suppose toward a contradiction that \(L/k\) is not separable. Then there is some \(\alpha\) with an inseparable (and irreducible) minimal polynomial \(f(x)\in k[x]\).

• Claim: since \(f\) is inseparable and irreducible, \(f(x) = g(x^p)\) for some \(g\in k[x]\).

  • Note: write \(g(x) \coloneqq\sum a_k x^k\), so that \(f(x) = \sum a_k (x^p)^k = \sum a_k x^{pk}\).

• This is a contradiction, since it makes \(f\) reducible by using the “Freshman’s dream”: \begin{align*} f(x) = \sum a_k x^{pk} = \qty{ \sum a_k^{1\over p} x^k}^p \coloneqq(h(x))^p .\end{align*}

• Proof of claim: in \(\operatorname{ch}k = p, f\) inseparable \(\implies f(x) = g(x^p)\).

  • Use that \(f\) is inseparable iff \(\gcd(f, f') \neq 1\), and since \(f\) is irreducible this forces \(f' \equiv 0\), so \(ka_k = 0\) for all \(k\).
  • Then \(a_k\neq 0\) forces \(p\divides k\), so \(f(x) = a_0 + a_px^p + a_{2p}x^{2p} + \cdots\) and one takes \(g(x) \coloneqq\sum a_{kp}x^{kp}\).

• A finite inseparable extension:

  • It’s a theorem that finite extensions of perfect fields are separable, so one needs a non-perfect field.
  • Take \(L/k \coloneqq{ \mathbf{F} }_p(t^{1\over p}) / { \mathbf{F} }_p(t)\), which is a degree \(p\) extension (although both fields are infinite are characteristic \(p\)).
  • Then the minimal polynomial of \(t\) is \(f(x) \coloneqq x^p - t \in { \mathbf{F} }_p(t)[x]\), where \(f'(x) = px^p \equiv 0\) Alternatively, just note that \(f\) factors as \(f(x) = (x-t^{1\over p})^p\) in \(L[x]\), which has multiple roots.

\({\mathbf{Z}}/2{\mathbf{Z}}\)?

\({\mathbf{Q}}(2^{1\over p}, \zeta_p)\), which has degree \(p(p-1)\) and is generated by the maps \begin{align*} \sqrt[p]{2} & \mapsto \sqrt[p]{2} \zeta^{a} \\ \zeta & \mapsto \zeta^{b} .\end{align*}

Part a:

• A finite extension \(E/F\) is Galois if it is normal and separable:
  • Normal: every \(f\in F[x]\) either has no roots in \(E\) or all roots in \(E\).
  • Separable: every element \(e\in E\) has a separable minimal polynomial \(m(x)\), i.e. \(m\) has no repeated roots.

Part b:

• Note \(f\) is irreducible by Eisenstein with \(p=7\), and since \({\mathbf{Q}}\) is perfect, irreducible implies separable.

• Writing \(L \coloneqq\operatorname{SF}(f)/{\mathbf{Q}}\), this is a Galois extension:

  • \(L\) is separable: it is a finite extension of a perfect field, which is automatically separable.
  • \(L\) is normal: \(L\) is the splitting field of a separable polynomial, and thus normal.

• Since \(f\) is degree 3, we have \(G\coloneqq{ \mathsf{Gal}}(L/k) \leq S_3\), and since \(G\) is a transitive subgroup the only possibilities are \begin{align*} G = S_3 \cong D_3, A_3 \cong C_3 .\end{align*}

• Factor \(x^3 - 7 = (x-\omega)(x-\zeta_3\omega)(x-\zeta_3^2\omega)\) where \(\omega \coloneqq 7^{1\over 3}\) and \(\zeta_3\) is a primitive 3rd root of unity. Then \(L = {\mathbf{Q}}(\zeta_3, \omega)\).

  • Aside: label the roots in this order, so \(r_1 = \omega, r_2 = \zeta_3\omega, r_3 = \zeta_3^2\omega\).

• Write \(\min_{\omega, {\mathbf{Q}}}(x) = x^3 - 7\) and let \(L_0/{\mathbf{Q}}\coloneqq{\mathbf{Q}}(\omega)/{\mathbf{Q}}\) yields \([L_0: {\mathbf{Q}}] = 3\).

• Write \(\min_{\zeta_3, {\mathbf{Q}}}(x) = (x^3-1)/(x-1) = x^2 + x + 1\), and note that this is still the minimal polynomial over \(L_0\) since \(L_0 \subseteq {\mathbf{R}}\) and \(\zeta_3 \in {\mathbf{C}}\setminus{\mathbf{R}}\). So \([L:L_0] = 2\).

• Counting in towers, \begin{align*} [L:{\mathbf{Q}}] = [L:L_0][L_0: {\mathbf{Q}}] = (2)(3) = 6 .\end{align*}

• But \({\sharp}S_3 = 6\) and \({\sharp}A_3 = 3\), so \(G = S_3\).

• Explicitly, since we can write \(\operatorname{SF}(f) = {\mathbf{Q}}(\omega, \zeta_3)\), we can find explicit generators: \begin{align*} \sigma: &\begin{cases} \omega &\mapsto \omega \\ \zeta_3 &\mapsto \zeta_3\cdot \zeta_3. \end{cases} && \implies \sigma \sim (1,2,3) \\ \tau: &\begin{cases} \omega &\mapsto \omega \\ \zeta_3 &\mapsto \overline{\zeta_3}. \end{cases} && \implies \tau \sim (2, 3) .\end{align*} So \(G = \left\langle{\sigma, \tau {~\mathrel{\Big\vert}~}\sigma^3, \tau^2}\right\rangle\).

Part c:

• Note that the subgroup lattice for \(S_3\) looks like the following:

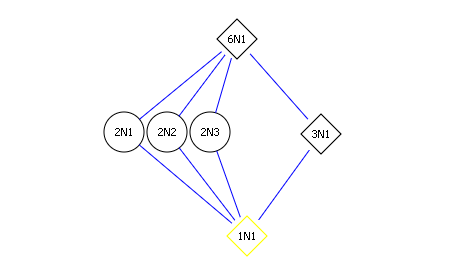
• Note that we can identify
  • \(\tau = (2,3)\) which fixes \(r_1\)
  • \(\sigma \tau = (1,2)\) which fixes \(r_3\)
  • \(\sigma^2\tau = (1, 3)\) which fixes \(r_2\)
  • \(\sigma = (1,2,3)\), for which we need to calculate the fixed field. Using that \(\sigma(\omega) =\zeta\omega\) and \(\sigma(\zeta)=\zeta\), supposing \(\sigma(\alpha) = \alpha\) we have \begin{align*} \sigma(\alpha) &\coloneqq\sigma(a + b\zeta_3 + c\zeta_3^2 + d\omega + e\zeta_3\omega + f\zeta_3^2\omega) \\ &= a + b\zeta_3 + c\zeta_3^2 + d\zeta_3\omega + e\zeta_3^2\omega + f\omega \\ \implies \alpha &= a + b\zeta_3 + c\zeta_3^2 + t_1(\omega + \zeta_3\omega + \zeta_3^2\omega) \\ \implies \alpha &= a + b\zeta_3 + c\zeta_3^2 + t_1\omega (1 + \zeta_3+ \zeta_3^2) \\ \implies \alpha &= a + b\zeta_3 + c\zeta_3^2 ,\end{align*} using the general fact that \(\sum_{k=0}^{n-1}\zeta_n^k = 0\). So the fixed field is \({\mathbf{Q}}(1, \zeta, \zeta^2) = {\mathbf{Q}}(\zeta)\).
• We thus get the following lattice correspondence:

Link to Diagram

• First consider \(g(z) \coloneqq z^2 + 4z + 64\). Applying the quadratic formula yields \begin{align*} z = {-4 \pm \sqrt{16 - 64} \over 2} = -2 \pm {1\over 2}\sqrt{ -15 \cdot 16 } = -2 \pm 2i \sqrt{15} .\end{align*}

• Substituting \(z=x^2\) yields the splitting field of \(f\) as \(L\coloneqq{\mathbf{Q}}(\pm \sqrt{ -2 \pm 2i\sqrt{15}})\).

  • Note that this factorization shows that \(f\) is irreducible over \({\mathbf{Q}}\), since the two quadratic factors have irrational coefficients and none of the roots are real.
  • Irreducible implies separable over a perfect field, so \(L/{\mathbf{Q}}\) is a separable extension.
  • \(L\) is the splitting field of a separable polynomial and thus normal, making \(L\) Galois.

• In this form, it’s not clear what the degree \([L:{\mathbf{Q}}]\) is, so we can find a better basis by rewriting the roots of \(g\): \begin{align*} z = -2 \pm 2i\sqrt{15} = \qty{\sqrt{5}}^2 - \qty{\sqrt 3}^2 \pm 2i\sqrt{5}\sqrt{3} = (\sqrt 5 \pm i\sqrt{3})^2 ,\end{align*} and so the roots of \(f\) are \(x = \pm \sqrt{5} \pm i\sqrt{3}\) and \(L = {\mathbf{Q}}(\sqrt 5, i\sqrt 3)\).

• Counting in towers, \begin{align*} [L:{\mathbf{Q}}] = [{\mathbf{Q}}(\sqrt 5, i \sqrt{3} ) : {\mathbf{Q}}\sqrt{5} ][{\mathbf{Q}}\sqrt{5} : {\mathbf{Q}}] = (2)(2) = 4 ,\end{align*} where we’ve used that \(\min_{\sqrt 5, {\mathbf{Q}}}(x) = x^2-5\) and \(\min_{i\sqrt 3, {\mathbf{Q}}}(x) = x^2 + 3\), which remains the minimal polynomial over \({\mathbf{Q}}(\sqrt 5) \subseteq {\mathbf{R}}\) since both roots are not real.

• So \(G\coloneqq{ \mathsf{Gal}}(L/{\mathbf{Q}}) \leq S_4\) is a transitive subgroup of size 4, making it either \(C_4\) or \(C_2^2\).

• Label the roots: \begin{align*} r_1 &= \sqrt 5 + i\sqrt 3 \\ r_2 &= \sqrt{5} - i \sqrt{3} \\ r_3 &= - \sqrt 5 + i\sqrt 3 = -r_2 \\ r_4 &= -\sqrt{5} - i\sqrt{3} = -r_1 .\end{align*}

• We can start writing down automorphisms: \begin{align*} \sigma_1: \begin{cases} \sqrt 5 &\mapsto -\sqrt 5 \\ i\sqrt 3 &\mapsto i\sqrt 3 . \end{cases} && \sigma_1 \sim (1,3)(2,4) \\ \sigma_2 \begin{cases} \sqrt 5 &\mapsto \sqrt 5 \\ i\sqrt 3 &\mapsto -i\sqrt 3 . \end{cases} && \sigma_2 \sim (1, 2)(3, 4) .\end{align*} Note that these define automorphisms because we’ve specified what happens to a basis and they send roots to other roots.

• Checking that \(\sigma_1^2 = \sigma_2^2 = \operatorname{id}\), this produces two distinct order 2 elements, forcing \(G \cong C_2^2\) since \(C_4\) only has one order 2 element. Explicitly, we have \begin{align*} C_2^2 \cong G = \left\langle{\tau_1, \tau_2}\right\rangle = \left\{{\operatorname{id}, \tau_1, \tau_2, \tau_1 \tau_2}\right\} = \left\{{\operatorname{id}, (1,3)(2,4), (1,2)(3,4), (1,4)(2,3) }\right\} ,\end{align*} and the generic subgroup lattice looks like:

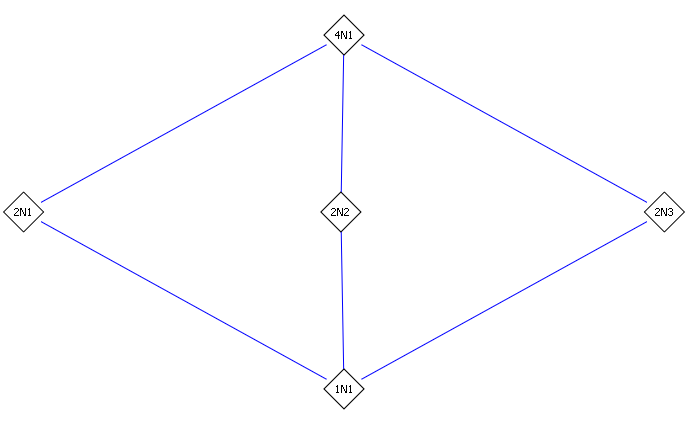
• Computing some fixed fields. Write \(i \sqrt{3} = x, \sqrt{5} = y\), then elements in the splitting field are of the form \(\alpha = 1 + ax + by + cxy\).

  • For \(\sigma_1\), we have \(x\mapsto -x\), so \begin{align*} \sigma_1(\alpha) = 1 - ax + by - cxy = \alpha \implies a=-a=0, c=-c=0 ,\end{align*} so this preserves \(1+by\), making the fixed field \({\mathbf{Q}}(1, y) = {\mathbf{Q}}(i \sqrt{3})\).

  • For \(\sigma_2\), we have \(y\mapsto -y\), so \begin{align*} \sigma_2(\alpha) = 1 +ax -by -cxy = \alpha \implies b=-b=0,c=-c=0 ,\end{align*} preserving \(1 + ax\) and making the fixed field \({\mathbf{Q}}(1, x) = {\mathbf{Q}}(\sqrt 5)\).

  • For \(\sigma_1 \sigma_2\), we have \(x\mapsto -x\) and \(y\mapsto -y\), so \begin{align*} \sigma_1\sigma_2(\alpha) = 1 -ax -by +cxy = \alpha \implies a=-a=-, b=-b=0 ,\end{align*} preserving \(1 + cxy\) and yielding \({\mathbf{Q}}(xy) = {\mathbf{Q}}(i\sqrt 3 \sqrt 5)\).

• So the lattice correspondence we get here is

Link to Diagram

\todo[inline]{Finish (c)}

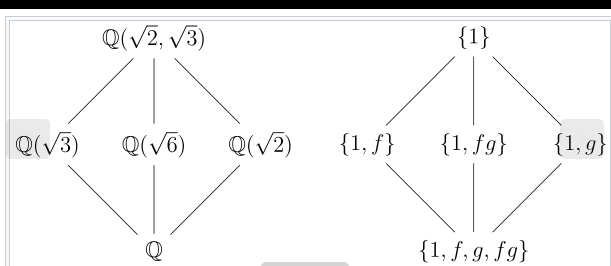
Let \(K = {\mathbf{Q}}(\zeta)\). Then \(K\) is the splitting field of \(f(x) = x^n - 1\), which is irreducible over \({\mathbf{Q}}\), so \(K/{\mathbf{Q}}\) is normal. We also have \(f'(x) = nx^{n-1}\) and \(\gcd(f, f') = 1\) since they can not share any roots.

Or equivalently, \(f\) splits into distinct linear factors \(f(x) = \prod_{k\leq n}(x-\zeta^k)\).

Since it is a Galois extension, \({\left\lvert {{ \mathsf{Gal}}(K/{\mathbf{Q}})} \right\rvert} = [K: {\mathbf{Q}}] = \phi(n)\) for the totient function.

We can now define maps \begin{align*} \tau_j: K &\to K \\ \zeta &\mapsto \zeta^j \end{align*} and if we restrict to \(j\) such that \(\gcd(n, j) = 1\), this yields \(\phi(n)\) maps. Noting that if \(\zeta\) is a primitive root, then \((n, j) = 1\) implies that that \(\zeta^j\) is also a primitive root, and hence another root of \(\min(\zeta, {\mathbf{Q}})\), and so these are in fact automorphisms of \(K\) that fix \({\mathbf{Q}}\) and thus elements of \({ \mathsf{Gal}}(K/{\mathbf{Q}})\).

So define a map \begin{align*} \theta: {\mathbf{Z}}_n^{\times}&\to K \\ [j]_n &\mapsto \tau_j .\end{align*}

from the multiplicative group of units to the Galois group.

The claim is that this is a surjective homomorphism, and since both groups are the same size, an isomorphism.

Let \(L/K/F\).

Let \(G\coloneqq{ \mathsf{Gal}}(K/F)\), then it suffices to show that \(G\) is always a solvable group, i.e. any group of order \(n=2015\) is solvable. Factor \(2015 = 5\cdot 13\cdot 31\) – this is a \(pqr\) factorization, and in fact any group with exactly 3 prime factors (so \(n\) is squarefree in particular) will be solvable. Let \(p=5, q=13, r=31\) so that \(p<q<r\). We aim to construct a composition series whose successive quotients are simple groups. Applying Sylow 3 yields

• \(n_p \divides qr, n_p \equiv 1 \operatorname{mod}p \implies n_5 \divides 13\cdot 31 = 403\) and \(n_5\equiv 1 \operatorname{mod}5\).
  • So \(n_5 \in \left\{{1, 13, 31}\right\}\) by divisibility and imposing the congruence forces \(n_5\in \left\{{1, 31}\right\}\) since \(13\not\equiv 1 \operatorname{mod}5\).
• \(n_q \divides pr, n_q \equiv 1 \operatorname{mod}q \implies n_{13} \divides 5\cdot 31 = 155\) and \(n_{13}\equiv 1 \operatorname{mod}13\).
  • So \(n_{13} \in \left\{{1,5,31}\right\}\) by divisibility and the congruence imposes \(n_{13}\in \left\{{1}\right\}\) since \(5,31 \not\equiv 1\operatorname{mod}13\). In particular, there is one Sylow 13-subgroup which is normal.
• \(n_r \divides pq, n_r \equiv 1 \operatorname{mod}r \implies n_{31} \divides 5 \cdot 13 = 65\) and \(n_{31}\equiv 1 \operatorname{mod}31\).
  • So \(n_{31}\in \left\{{1,5,13}\right\}\) by divisibility and the congruence imposes \(n_{31}\in \left\{{1}\right\}\) since \(5,13 \not\equiv 1\operatorname{mod}31\). In particular, the one Sylow 31-subgroup is normal.

Let \(H_{13}, H_{31}\) be the two normal subgroups of \(G\). Taking the quotient \(\tilde G \coloneqq G/H_{31}\) yields a group of order \(5\cdot 13\), and a similar argument as above using the Sylow theorems shows that \(\tilde G\) has a normal subgroup of order 13. By the subgroup correspondence theorem, this yields a normal subgroup \(N_1{~\trianglelefteq~}G\) containing \(H_{31}\) which has order \(13\cdot 31\). So define \(N_2 \coloneqq H_{31}\) to obtain \begin{align*} G \trianglerighteq N_1 \trianglerighteq N_2 \coloneqq H_{31} \trianglerighteq 0 .\end{align*} Since the quotients \(N_i/N_{i+1}\) have prime power order, they are cyclic and thus simple. We know \(N_1\) is normal in \(G\) since it came from extending a normal group in a quotient, and we know \(N_2\) is normal in \(N_1\) since it was normal in all of \(G\). So \(G\) is solvable.

• Suppose \(a\) is not a \(p\)th power in \(F\), then \(f(x) \coloneqq x^p-a\) has no roots in \(F\).
• Toward a contradiction, suppose \(f\) is reducible in \(F[x]\).
• In \(\operatorname{SF}(f)\), since \(\operatorname{ch}F = p\) we have \(f(x) = (x-\zeta)^p\) for some \(\zeta = a^{1\over p}\).
  • So if \(f\) is reducible in \(F[x]\), we have \(f(x) = p_1(x) p_2(x)\) where \(p(x) = (x-\zeta)^q\in F[x]\) for some \(1\leq q < p\), since these are the only factors of \(f\).
  • The claim is that \(\zeta\in F\) as well, which is a contradiction since \(\zeta\) is a \(p\)th root of \(a\).
• We have \(x^q-\zeta^q \in F[x]\), so \(\zeta^q\in F\).
• We know \(a = \zeta^p\in F\), and thus \(\zeta^{d} = \zeta\in F\) for \(d \coloneqq\gcd(p, n) = 1\). \(\contradiction\)
  • Why this is true: write \(d = \gcd(p, n)\) in \({\mathbf{Z}}\) to obtain \(d = tp + sn\) for some \(t, s\).
  • Then \(\zeta^d = \zeta^{tp+sn} = (\zeta^p)^t \cdot (\zeta^n)^s \in F\).

• WTS: \(f(x) \coloneqq x^p - a\in { \mathbf{F} }[x]\) reducible \(\implies f\) has a root in the base field \({ \mathbf{F} }\).

• Write \(f(x) = g(x) h(x)\) and factor \(f(x) = \prod_{i=1}^p (x- r_i) \in \operatorname{SF}(f)[x]\) where the \(r_i\) are not necessarily distinct roots.

• WLOG, \(g(x) = \prod_{i=1}^\ell (x-r_i)\) for some \(1\leq \ell \leq p-1\), i.e. rearrange the factors so that \(g\) is the first \(\ell\) of them.

  • \(\ell \neq 1, p\) since \(f\) is reducible, making \(g, h\) nonconstant.

• Set \(R_\ell \coloneqq\prod_{i=1}^\ell r_i\), which is the constant term in \(g\), so \(R_\ell \in { \mathbf{F} }\) since \(g\in { \mathbf{F} }[x]\).

• Each \(r_i\) is a root of \(f\), so \(r_i^p - a = 0\) for all \(i\), so \(r_i^p = a\).

• Trick: what is the \(p\)th power of \(R_\ell\)? \begin{align*} R_\ell^p &\coloneqq\qty{ \prod_{i=1}^\ell}^p \\ &= \prod_{i=1}^\ell r_i^p \\ &= \prod_{i=1}^\ell a \\ &= a^\ell ,\end{align*} so \(R_\ell^p = a^\ell\).

• Use Bezout: \(\gcd(\ell, p) = 1\) since \(p\) is prime, so write \(tp + s\ell = 1\) for some \(t,s\in {\mathbf{Z}}\)

• Use this to build a root of \(f\) that’s in \({ \mathbf{F} }\): write \begin{align*} a &= a^1\\ &= a^{tp + s\ell} \\ &= a^{tp} a^{s\ell} \\ &=a^{tp} (a^\ell)^s\\ &= a^{tp} (R_\ell^p)^s \\ &= (a^t R_\ell^s)^p \\ &\coloneqq\beta^p ,\end{align*} so \(a = \beta^p\).

  • Check \(\beta\in { \mathbf{F} }\): use that \(R_\ell \in { \mathbf{F} }\) since it was a constant term of a polynomial in \({ \mathbf{F} }[x]\), \(a\in { \mathbf{F} }\) by assumption, and fields are closed under taking powers and products.

Consider \(L \coloneqq{ \mathbf{F} }_p[x]/(x^{p^\ell} - x)\), this yields a field extension \(L/{ \mathbf{F} }_p\) with \([L: { \mathbf{F} }_p] = \ell\) and so \(L\cong { \mathbf{F} }_{p^\ell}\) is the splitting field of \(x^{p^\ell} - x\). Note that \(x^{p^\ell}-x\) is the product of all monic irreducible polynomials in \({ \mathbf{F} }_p[x]\) of degree dividing \(\ell\), and since \(\ell\) is prime, the only such polynomials are of degrees \(1\) or \(\ell\) – this follows because any such polynomial would generate an intermediate extension \(L'\) with \(L/L'/{ \mathbf{F} }_p\), and multiplicativity in towers yields \begin{align*} [L:{ \mathbf{F} }_p] = [L: L'] \cdot [L' : { \mathbf{F} }_p] = \ell ,\end{align*} forcing either \([L: L'] = 1\) or \([L': { \mathbf{F} }_p] = 1\).

Let \(P\) be the desired number of monic irreducible degree \(\ell\) polynomials in \({ \mathbf{F} }_p[x]\). The idea is now to get a formula involving all monic irreducible (not necessarily degree \(\ell\)) polynomials and use it to solve for \(P\). By the above observation, we have a factorization \begin{align*} x^{p^\ell} - x = \prod_{i\in I} f_i(x) = \prod_{i\in I_1} f_i(x) \cdot \prod_{i\in I_2} g_i(x) ,\end{align*} where \(I\) is the set of all monic irreducible polynomials, and the above observation shows \(I = I_1{\textstyle\coprod}I_2\) where \(I_1\) are those of degree 1 and \(I_2\) are those of degree \(\ell\). Taking degrees of both sides yields \begin{align*} p^\ell = \sum_{i\in I_1} \deg f_i(x) + \sum_{i\in I_2} \deg g_i(x) = \sum_{i\in I_1} 1 + P\ell = {\sharp}I_1 + P\ell ,\end{align*} since each \(\deg f_i(x) = 1\) and there are \({\sharp}I_1\) many of them, and \(\deg g_i(x) = \ell\) and there are \(P\) of them. Rearranging yields \begin{align*} P\ell = p^\ell - {\sharp}I_1 \implies P = \ell^{-1}\qty{p^\ell - {\sharp}I_1} ,\end{align*} and so it suffices to determine \({\sharp}I_1\), the number of monic linear irreducible polynomials in \({ \mathbf{F} }_p[x]\). These are all of the form \(x + a\) where \(a\in { \mathbf{F} }_p\), and there are \(p\) choices for \(a\), so the final count is \begin{align*} P = \ell^{-1}\qty{p^\ell - p} .\end{align*}

Let \(K = {\mathbf{Q}}(\zeta)\).