Group Theory
Centralizing and Normalizing
-
Show that \(C_G(H) \subseteq N_G(H) \leq G\).
-
Show that \(Z(G) \subseteq C_G(H) \subseteq N_G(H)\).
-
Given \(H\subseteq G\), let \(S(H)= \bigcup_{g\in G} gHg^{-1}\), so \({\left\lvert {S(H)} \right\rvert}\) is the number of conjugates to \(H\). Show that \({\left\lvert {S(H)} \right\rvert} = [G : N_G(H)]\).
- That is, the number of subgroups conjugate to \(H\) equals the index of the normalizer of \(H\).
-
Show that \(Z(G) = \bigcap_{a\in G} C_G(a)\).
-
Show that the centralizer \(G_G(H)\) of a subgroup is again a subgroup.
-
Show that \(C_G(H) {~\trianglelefteq~}N_G(H)\) is a normal subgroup.
-
Show that \(C_G(G) = Z(G)\).
-
Show that for \(H\leq G\), \(C_H(x) = H \cap C_G(x)\).
-
Let \(H, K \leq G\) a finite group, and without using the normalizers of \(H\) or \(K\), show that \({\left\lvert {HK} \right\rvert} = {\left\lvert {H} \right\rvert} {\left\lvert {K} \right\rvert}/{\left\lvert {H\cap K} \right\rvert}\).
-
Show that if \(H \leq N_G(K)\) then \(HK \leq H\), and give a counterexample showing that this condition is necessary.
-
Show that \(HK\) is a subgroup of \(G\) iff \(HK = KH\).
-
Prove that the kernel of a homomorphism is a normal subgroup.
Primes in Group Theory
-
Show that any group of prime order is cyclic and simple.
-
Analyze groups of order \(pq\) with \(q<p\).
Hint: consider the cases when \(p\) does or does not divide \(q-1\).
- Show that if \(q\) does not divide \(p-1\), then \(G\) is cyclic.
- Show that \(G\) is never simple.
-
Analyze groups of order \(p^2 q\).
Hint: Consider the cases when \(q\) does or does not divide \(p^2 - 1\).
-
Show that no group of order \(p^2 q^2\) is simple for \(p<q\) primes.
-
Show that a group of order \(p^2 q^2\) has a normal Sylow subgroup.
-
Show that a group of order \(p^2 q^2\) where \(q\) does not divide \(p^2-1\) and \(p\) does not divide \(q^2-1\) is abelian.
-
Show that every group of order \(pqr\) with \(p<q<r\) primes contains a normal Sylow subgroup.
- Show that \(G\) is never simple.
-
Let \(p\) be a prime and \({\left\lvert {G} \right\rvert} = p^3\). Prove that \(G\) has a normal subgroup \(N\) of order \(p^2\).
-
Suppose \(N = \left\langle{h}\right\rangle\) is cyclic and classify all possibilities for \(G\) if:
- \({\left\lvert {h} \right\rvert} = p^3\)
- \({\left\lvert {h} \right\rvert} = p\).
Hint: Sylow and semidirect products.
-
-
Show that any normal \(p{\hbox{-}}\) subgroup is contained in every Sylow \(p{\hbox{-}}\)subgroup of \(G\).
-
Show that the order of \(1+p\) in \(\qty{{\mathbf{Z}}/p^2{\mathbf{Z}}}^{\times}\) is equal to \(p\). Use this to construct a non-abelian group of order \(p^3\).
p-Groups
-
Show that every \(p{\hbox{-}}\)group has a nontrivial center.
-
Show that every \(p{\hbox{-}}\)group is nilpotent.
-
Show that every \(p{\hbox{-}}\)group is solvable.
-
Show that every maximal subgroup of a \(p{\hbox{-}}\)group has index \(p\).
-
Show that every maximal subgroup of a \(p{\hbox{-}}\)group is normal.
-
Show that every group of order \(p\) is cyclic.
-
Show that every group of order \(p^2\) is abelian and classify them.
-
Show that every normal subgroup of a \(p{\hbox{-}}\)group is contained in the center.
Hint: Consider \(G/Z(G)\).
-
Let \(O_P(G)\) be the intersection of all Sylow \(p{\hbox{-}}\)subgroups of \(G\). Show that \(O_p(G) {~\trianglelefteq~}G\), is maximal among all normal \(p{\hbox{-}}\)subgroups of \(G\)
-
Let \(P\in {\operatorname{Syl}}_p(H)\) where \(H{~\trianglelefteq~}G\) and show that \(P\cap H \in {\operatorname{Syl}}_p(H)\).
-
Show that Sylow \(p_i{\hbox{-}}\)subgroups \(S_{p_1}, S_{p_2}\) for distinct primes \(p_1\neq p_2\) intersect trivially.
-
Show that in a \(p\) group, every normal subgroup intersects the center nontrivially.
Symmetric Groups
Specific Groups
- Show that the center of \(S_3\) is trivial.
- Show that \(Z(S_n) = 1\) for \(n\geq 3\)
- Show that \(\mathop{\mathrm{Aut}}(S_3) = \mathop{\mathrm{Inn}}(S_3) \cong S_3\).
- Show that the transitive subgroups of \(S_3\) are \(S_3, A_3\)
- Show that the transitive subgroups of \(S_4\) are \(S_4, A_4, D_4, {\mathbf{Z}}_2^2, {\mathbf{Z}}_4\).
- Show that \(S_4\) has two normal subgroups: \(A_4, {\mathbf{Z}}_2^2\).
- Show that \(S_{n\geq 5}\) has one normal subgroup: \(A_n\).
- \(Z(A_n) = 1\) for \(n\geq 4\)
- Show that \([S_n, S_n] = A_n\)
- Show that \([A_4, A_4] \cong {\mathbf{Z}}_2^2\)
- Show that \([A_n, A_n] = A_n\) for \(n\geq 5\), so \(A_{n\geq 5}\) is nonabelian.
General Structure
- Show that an \(m{\hbox{-}}\)cycle is an odd permutation iff \(m\) is an even number.
- Show that a permutation is odd iff it has an odd number of even cycles.
- Show that the center of \(S_n\) for \(n\geq 4\) is nontrivial.
- Show that disjoint cycles commute.
- Show directly that any \(k{\hbox{-}}\)cycle is a product of transpositions, and determine how many transpositions are needed.
Generating Sets
-
Show that \(S_n\) is generated by any of the following types of cycles:
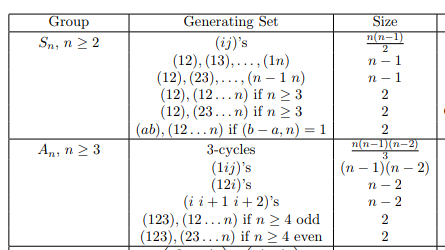
- Show that \(S_n\) is generated by transpositions.
- Show that \(S_n\) is generated by adjacent transpositions.
- Show that \(S_n\) is generated by \(\left\{{(12), (12\cdots n)}\right\}\) for \(n\geq 2\)
- Show that \(S_n\) is generated by \(\left\{{(12), (23\cdots n)}\right\}\) for \(n\geq 3\)
- Show that \(S_n\) is generated by \(\left\{{(ab), (12\cdots n)}\right\}\) where \(1\leq a<b\leq n\) iff \(\gcd(b-a, n) = 1\).
- Show that \(S_p\) is generated by any arbitrary transposition and any arbitrary \(p{\hbox{-}}\)cycle.
Alternating Groups
- Show that \(A_n\) is generated \(3{\hbox{-}}\)cycles.
- Prove that \(A_n\) is normal in \(S_n\).
- Argue that \(A_n\) is simple for \(n \geq 5\).
- Show that \(\mathop{\mathrm{Out}}(A_4)\) is nontrivial.
Dihedral Groups
- Show that if \(N{~\trianglelefteq~}D_n\) is a normal subgroup of a dihedral group, then \(D_n/N\) is again a dihedral group.
Other Groups
- Show that \({\mathbf{Q}}\) is not finitely generated as a group.
- Show that the Quaternion group has only one element of order 2, namely \(-1\).
Classification
-
Show that no group of order 36 is simple.
-
Show that no group of order 90 is simple.
-
Classifying all groups of order 99.
-
Show that all groups of order 45 are abelian.
-
Classify all groups of order 10.
-
Classify the five groups of order 12.
-
Classify the four groups of order 28.
-
Show that if \({\left\lvert {G} \right\rvert} = 12\) and has a normal subgroup of order 4, then \(G \cong A_4\).
-
Suppose \({\left\lvert {G} \right\rvert} = 240 = s^4 \cdot 3 \cdot 5\).
- How many Sylow-\(p\) subgroups does \(G\) have for \(p\in \left\{{2, 3, 5}\right\}\)?
- Show that if \(G\) has a subgroup of order 15, it has an element of order 15.
- Show that if \(G\) does not have such a subgroup, the number of Sylow-\(3\) subgroups is either 10 or 40.
Hint: Sylow on the subgroup of order 15 and semidirect products.
Group Actions
- Show that the stabilizer of an element \(G_x\) is a subgroup of \(G\).
- Show that if \(x, y\) are in the same orbit, then their stabilizers are conjugate.
- Show that the stabilizer of an element need not be a normal subgroup?
- Show that if \(G \curvearrowright X\) is a group action, then the stabilizer \(G_x\) of a point is a subgroup.
Series of Groups
-
Show that \(A_n\) is simple for \(n\geq 5\)
-
Give a necessary and sufficient condition for a cyclic group to be solvable.
-
Prove that every simple abelian group is cyclic.
-
Show that \(S_n\) is generated by disjoint cycles.
-
Show that \(S_n\) is generated by transpositions.
-
Show if \(G\) is finite, then \(G\) is solvable \(\iff\) all of its composition factors are of prime order.
-
Show that if \(N\) and \(G/N\) are solvable, then \(G\) is solvable.
-
Show that if \(G\) is finite and solvable then every composition factor has prime order.
-
Show that \(G\) is solvable iff its derived series terminates.
-
Show that \(S_3\) is not nilpotent.
-
Show that \(G\) nilpotent \(\implies G\) solvable
-
Show that nilpotent groups have nontrivial centers.
-
Show that Abelian \(\implies\) nilpotent
-
Show that p-groups \(\implies\) nilpotent
Misc
-
Prove Burnside’s theorem.
-
Show that \(\mathop{\mathrm{Inn}}(G) {~\trianglelefteq~}Aut(G)\)
-
Show that \(\mathop{\mathrm{Inn}}(G) \cong G / Z(G)\)
-
Show that the kernel of the map \(G\to \mathop{\mathrm{Aut}}(G)\) given by \(g\mapsto (h\mapsto ghg^{-1})\) is \(Z(G)\).
-
Show that \(N_G(H) / C_G(H) \cong A \leq Aut(H)\)
-
Give an example showing that normality is not transitive: i.e. \(H{~\trianglelefteq~}K {~\trianglelefteq~}G\) with \(H\) not normal in \(G\).
Nonstandard Topics
-
Show that \(H~\text{char}~G \Rightarrow H \unlhd G\)
Thus “characteristic” is a strictly stronger condition than normality
-
Show that \(H ~\text{char}~ K ~\text{char}~G \Rightarrow H ~\text{char}~ G\)
So “characteristic” is a transitive relation for subgroups.
-
Show that if \(H \leq G\), \(K{~\trianglelefteq~}G\) is a normal subgroup, and \(H~\text{char}~K\) then \(H\) is normal in \(G\).
So normality is not transitive, but strengthening one to “characteristic” gives a weak form of transitivity.