940 Extra Problems Galois Theory

Galois Theory

Show that if $K/F$ is the splitting field of a separable polynomial then it is Galois.
Show that any quadratic extension of a field $F$ with $\operatorname{ch}(F)\neq 2$ is Galois.
Show that if $K/E/F$ with $K/F$ Galois then $K/E$ is always Galois with $g(K/E) \leq g(K/F)$ .
- Show additionally $E/F$ is Galois $\iff g(K/E) {~\trianglelefteq~}g(K/F)$ .
- Show that in this case, $g(E/F) = g(K/F) / g(K/E)$ .
Show that if $E/k, F/k$ are Galois with $E\cap F = k$ , then $EF/k$ is Galois and $G(EF/k) \cong G(E/k)\times G(F/k)$ .

Show that the Galois group of $x^n - 2$ is $D_n$ , the dihedral group on $n$ vertices.
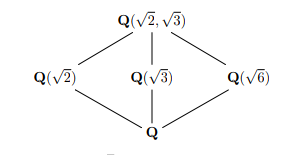
Compute all intermediate field extensions of ${\mathbf{Q}}(\sqrt 2, \sqrt 3)$ , show it is equal to ${\mathbf{Q}}(\sqrt 2 + \sqrt 3)$ , and find a corresponding minimal polynomial.

figures/image_2020-06-01-20-56-35.png

Compute all intermediate field extensions of ${\mathbf{Q}}(2^{1\over 4}, \zeta_8)$ .
Show that ${\mathbf{Q}}(2^{1\over 3})$ and ${\mathbf{Q}}(\zeta_3 2^{1\over 3})$
Show that if $L/K$ is separable, then $L$ is normal $\iff$ there exists a polynomial $p(x) = \prod_{i=1}^n x- \alpha_i\in K[x]$ such that $L = K(\alpha_1, \cdots, \alpha_n)$ (so $L$ is the splitting field of $p$ ).
Is ${\mathbf{Q}}(2^{1\over 3})/{\mathbf{Q}}$ normal?
Show that ${\mathbf{GF}}(p^n)$ is the splitting field of $x^{p^n} - x \in { \mathbf{F} }_p[x]$ .
Show that ${\mathbf{GF}}(p^d) \leq {\mathbf{GF}}(p^n) \iff d\divides n$
Compute the Galois group of $x^n - 1 \in {\mathbf{Q}}[x]$ as a function of $n$ .
Identify all of the elements of the Galois group of $x^p-2$ for $p$ an odd prime (note: this has a complicated presentation).
Show that ${ \operatorname{Gal}}(x^{15}+2)/{\mathbf{Q}}\cong S_2 \rtimes{\mathbf{Z}}/15{\mathbf{Z}}$ for $S_2$ a Sylow $2{\hbox{-}}$ subgroup.
Show that ${ \operatorname{Gal}}(x^3+4x+2)/{\mathbf{Q}}\cong S_3$ , a symmetric group.