I’d like to extend my gratitude to the following people for helping supply solutions and proofs:
- Paco Adajar
- Swaroop Hegde
Many other solutions contain input and ideas from other graduate students and faculty members at UGA, along with questions and answers posted on Math Stack Exchange or Math Overflow.
Group Theory: General
Permutations
Fall 2021 #1
Let \(G\) be a group. An automorphism \(\phi: G \rightarrow G\) is called inner if the automorphism is given by conjugation by a fixed group element \(g\), i.e., \begin{align*} \phi=\phi_{g}: h \mapsto g h g^{-1} . \end{align*}
-
Prove that the set of inner automorphisms forms a normal subgroup of the group of all automorphisms of \(G\).
-
Give an example of a finite group with an automorphism which is not inner.
-
Denote by \(S_{n}\) the group of permutations of the set \(\{1, \ldots, n\}\). Suppose that \(g \in S_{n}\) sends \(i\) to \(g_{i}\) for \(i=1, \ldots, n .\) Let \((a, b)\) denote as usual the cycle notation for the transposition which permutes \(a\) and \(b\). For \(i \in\{1, \ldots, n-1\}\), compute \(\phi_{g}((i, i+1))\).
-
Suppose that an automorphism \(\phi \in \operatorname{Aut}\left(S_{n}\right)\) preserves cycle type, i.e., that for every element \(s\) of \(S_{n}, s\) and \(\phi(s)\) have the same cycle type. Show that \(\phi\) is inner.
Hint: Consider the images of generators \(\phi((1,2)), \phi((2,3)), \cdots, \phi((n-1, n))\).
Cosets
Spring 2020 #2
Let \(H\) be a normal subgroup of a finite group \(G\) where the order of \(H\) and the index of \(H\) in \(G\) are relatively prime. Prove that no other subgroup of \(G\) has the same order as \(H\).
- Division algorithm: \((a,b)= d\implies as+bt =1\) for some \(s, t\).
- Coset containment trick: \(X\subseteq N \iff xN = N\) for all \(x\).
Recognize that it suffices to show \(hN = N\). Context cue: coprimality hints at division algorithm. Descend to quotient so you can leverage both the order of \(h\) and the order of cosets simultaneously.
- For ease of notation, replace \(H\) in the problem with \(N\) so we remember which one is normal.
- Write \(n\coloneqq{\sharp}N\) and \(m \coloneqq[G:N] = {\sharp}G/N\), where the quotient makes sense since \(N\) is normal.
-
Let \(H \leq G\) with \({\sharp}H = n\), we’ll show \(H=N\).
- Since \({\sharp}H = {\sharp}N\) it suffices to show \(H \subseteq N\).
- It further suffices to show \(hN = N\) for all \(h\in H\).
- Noting \(\gcd(m, n)=1\), use the division algorithm to write \(1 = ns + mt\) for some \(s,t\in {\mathbf{Z}}\).
-
The result follows from a computation:
\begin{align*}
hN
&= h^1 N \\
&= h^{ns + mt}N \\
&= h^{ns} N \cdot h^{mt}N \\
&= \qty{h^n N}^s \cdot \qty{h^t N}^m \\
&= (eN)^s \cdot N \\
&= N
,\end{align*}
- We’ve used that \(h\in H \implies o(h) \divides {\sharp}H = n\) by Lagrange, so \(h^n = e\).
- We’ve also used that \({\sharp}G/N = m\), so \((xH)^m = H\) for any \(xH\in G/H\).
Fall 2014 #6
Let \(G\) be a group and \(H, K < G\) be subgroups of finite index. Show that \begin{align*} [G: H\cap K] \leq [G: H] ~ [G:K] .\end{align*}
- For \(H, K\leq G\), intersection is again a subgroup of everything: \(H\cap K \leq H, K, G\) by the one-step subgroup test.
- Counting in towers: \(A\leq B \leq C \implies [C:A] = [C:B][B:A]\).
- Fundamental theorem of cosets: \(xH = yH \iff xy^{-1}\in H\).
- Common trick: just list out all of the darn cosets!
Count in towers, show that distinct coset reps stay distinct.
- \(H \cap K \leq H \leq G \implies [G: H \cap K] = [G: H] [H : H \cap K]\)
- So it suffices to show \([H: H \cap K] \leq [G: K]\)
- Write \(H/H \cap K = \left\{{ h_1 J, \cdots, h_m J }\right\}\) as distinct cosets where \(J \coloneqq H \cap J\).
- Then \(h_i J\neq h_j J \iff h_i h_j^{-1}\not\in J = H \cap K\).
- \(H\) is a subgroup, so \(h_i h_j^{-1}\in H\) forces this not to be in \(K\).
- But then \(h_i K \neq h_j K\), so these are distinct cosets in \(G/K\).
- So \({\sharp}G/K \geq m\).
Spring 2013 #3
Let \(P\) be a finite \(p{\hbox{-}}\)group. Prove that every nontrivial normal subgroup of \(P\) intersects the center of \(P\) nontrivially.
\todo[inline]{Clean up, sketchy argument.}
- Let \(N{~\trianglelefteq~}P\), then for each conjugacy class \([n_i]\) in \(N\), \(H \cap[g_i] = [g_i]\) or is empty.
- \(G = {\textstyle\coprod}_{i\leq M} [g_i]\) is a disjoint union of conjugacy classes, and the conjugacy classes of \(H\) are of the form \([g_i] \cap H\).
- Then pull out the center \begin{align*} H = \coprod_{i\leq M} [g_i] \cap H = \qty{ Z(G) \cap H } {\textstyle\coprod}\coprod_{i\leq M'} [g_i] .\end{align*}
- Taking cardinalities, \begin{align*} {\sharp}H = {\sharp}\qty{ Z(G) \cap H} + \sum_{i\leq M'} {\sharp}[g_i] .\end{align*}
- \(p\) divides \(H\) since \(H\leq P\) and \(P\) is a \(p{\hbox{-}}\)group.
- Each \({\sharp}[g_i] \geq 2\) since the trivial conjugacy classes appear in the center, forcing \({\sharp}[g_i] \geq p\).
- \(p\) divides \({\sharp}[g_i]\) since \({\sharp}[g_i]\) must divide \({\sharp}P = p^k\)
- So \(p\) must divide the remaining term \(Z(G) \cap H\), which makes it nontrivial.
Burnside / Class Equation
Spring 2019 #4
For a finite group \(G\), let \(c(G)\) denote the number of conjugacy classes of \(G\).
-
Prove that if two elements of \(G\) are chosen uniformly at random,then the probability they commute is precisely \begin{align*} \frac{c(G)}{{\left\lvert {G} \right\rvert}} .\end{align*}
-
State the class equation for a finite group.
- Using the class equation (or otherwise) show that the probability in part (a) is at most \begin{align*} \frac 1 2 + \frac 1 {2[G : Z(G)]} .\end{align*}
Here, as usual, \(Z(G)\) denotes the center of \(G\).
(DZG) This is a slightly anomalous problem! It’s fun and worth doing, because it uses the major counting formulas. Just note that the techniques used in this problem perhaps don’t show up in other group theory problems.
- Notation: \(X/G\) is the set of \(G{\hbox{-}}\)orbits
- Notation: \(X^g = \left\{{x\in X{~\mathrel{\Big\vert}~}g\cdot x = x}\right\}\)
- Burnside’s formula: \({\sharp}{X/G} = {1 \over {\sharp}G} \sum {\sharp}{X^g}\).
- Definition of conjugacy class: \(C(g) = \left\{{ hgh^{-1}{~\mathrel{\Big\vert}~}h\in G }\right\}\).
Fixed points of the conjugation action are precisely commuting elements. Apply Burnside. Context clue: \(1/[G:Z(G)]\) is weird, right? Use that \([G:Z(G)] = {\sharp}G/{\sharp}Z(G)\), so try to look for \({\sharp}Z(G)/{\sharp}(G)\) somewhere. Count sizes of centralizers.
-
Define a sample space \(\Omega = G \times G\), so \({\sharp}{\Omega} = ({\sharp}{G})^2\).
-
Identify the event we want to analyze: \begin{align*} A \coloneqq\left\{{(g,h) \in G\times G {~\mathrel{\Big\vert}~}[g,h] = 1}\right\} \subseteq \Omega .\end{align*}
-
Note that the slices are centralizers: \begin{align*} A_g \coloneqq\left\{{(g, h) \in \left\{{ g }\right\} \times G {~\mathrel{\Big\vert}~}[g, h] = 1}\right\} = Z(g) \implies A = \coprod_{g\in G} Z(g) .\end{align*}
-
Set \(n\) be the number of conjugacy classes, note we want to show \(P(A) = n / {\left\lvert {G} \right\rvert}\).
-
Let \(G\) act on itself by conjugation, which partitions \(G\) into conjugacy classes.
-
What are the orbits? \begin{align*} \mathcal{O}_g = \left\{{hgh^{-1}{~\mathrel{\Big\vert}~}h\in G}\right\} ,\end{align*} which is the conjugacy class of \(g\). In particular, the number of orbits is the number of conjugacy classes.
-
What are the fixed points? \begin{align*}X^g = \left\{{h\in G {~\mathrel{\Big\vert}~}hgh^{-1}= g}\right\},\end{align*} which are the elements of \(G\) that commute with \(g\), which is isomorphic to \(A_g\).
-
-
Identifying centralizers with fixed points, \begin{align*} {\sharp}{A} = {\sharp}{\coprod_{g\in G} Z(g) } = \sum_{g\in G} {\sharp}{Z(g)} = \sum_{g\in G}{\sharp}{X^g} .\end{align*}
-
Apply Burnside \begin{align*} {\sharp}{X / G} = \frac { 1 } { {\sharp}G } \sum _ { g \in G } {\sharp}X ^ { g } , \end{align*}
-
Note \({\sharp}{X/G} = n\), i.e. the number of conjugacy classes is the number of orbits.
-
Rearrange and use definition: \begin{align*} n \cdot {\sharp}{G} = \qty{{\sharp}{X/G} }\cdot {\sharp}{G} = \sum _ { g \in G } {\sharp}X ^ { g } \end{align*}
-
Compute probability: \begin{align*} P(A) = {{\sharp}A \over {\sharp}\Omega} = \sum _{ g \in G } \frac{{\sharp}X ^ { g }}{ ( {\sharp}{G} )^2} = \frac{\qty{ {\sharp}{X/G}} \cdot {\sharp}{G}}{ ({\sharp}{G})^2} = \frac{n \cdot {\sharp}{G}}{( {\sharp}{G} )^2} = \frac n {{\sharp}G} .\end{align*}
Statement of the class equation: \begin{align*} {\left\lvert {G} \right\rvert} = Z(G) + \sum_{\substack{\text{One $x$ from each} \\ \text{conjugacy class}}}[G: Z(x)] \end{align*} where \(Z(x) = \left\{{g\in G {~\mathrel{\Big\vert}~}[g, x] = 1}\right\}\) is the centralizer of \(x\) in \(G\).
(DZG): I couldn’t convince myself that a previous proof using the class equation actually works. Instead, I’ll borrow the proof from this note
- Write the event as \(A = \coprod_{g\in G} \left\{{g}\right\} \times Z(g)\), then \begin{align*} P(A) = {{\sharp}A\over ({\sharp}G)^2} = {1\over ({\sharp}G)^2} \sum_{g\in G} {\sharp}Z(g) .\end{align*}
-
Attempt to estimate the sum: pull out central elements \(g\in Z(G)\).
- Note \(Z(g) = G\) for central \(g\), so \({\sharp}Z(g) = {\sharp}G\)
- Note \begin{align*} g\not\in Z(G)\implies {\sharp}Z(g) \leq {1\over 2} {\sharp}G ,\end{align*} since \(Z(g) \leq G\) is a subgroup, and \begin{align*} [G:Z(g)] \neq 1 \implies [G: Z(g)] \geq 2 .\end{align*}
- Use these facts to calculate: \begin{align*} P(A) &= {1\over ({\sharp}G)^2 } \qty{ \sum_{g\in Z(g)} {\sharp}Z(g) + \sum_{g\not\in Z(g)} {\sharp}Z(g) } \\ &= {1\over ({\sharp}G)^2 } \qty{ \sum_{g\in Z(g)} {\sharp}G + \sum_{g\not\in Z(g)} {\sharp}Z(g) } \\ &= {1\over ({\sharp}G)^2 } \qty{ {\sharp}Z(G) \cdot {\sharp}G + \sum_{g\not\in Z(g)} {\sharp}Z(g) } \\ &\leq {1\over ({\sharp}G)^2 } \qty{ {\sharp}Z(G) \cdot {\sharp}G + \sum_{g\not\in Z(g)} {1\over 2} {\sharp}G } \\ &= {1\over ({\sharp}G)^2 } \qty{ {\sharp}Z(G) \cdot {\sharp}G + \qty{ \sum_{g\not\in Z(g)} {1\over 2} } \cdot {\sharp}G } \\ &= {1\over ({\sharp}G) } \qty{ {\sharp}Z(G) + \sum_{g\not\in Z(g)} {1\over 2} } \\ &= {1\over ({\sharp}G) } \qty{ {\sharp}Z(G) + {1\over 2} \sum_{g\not\in Z(g)} 1 } \\ &= {1\over ({\sharp}G) } \qty{ {\sharp}Z(G) + {1\over 2} {\sharp}(G \setminus Z(G) ) } \\ &= {1\over ({\sharp}G) } \qty{ {\sharp}Z(G) + {1\over 2} {\sharp}G - {1\over 2} {\sharp}Z(G) } \\ &= {1\over ({\sharp}G) } \qty{ {1\over 2} {\sharp}Z(G) + {1\over 2} {\sharp}G } \\ &= {1\over 2} \qty{1 + { {\sharp}Z(G) \over {\sharp}G }} \\ &= {1\over 2} \qty{1 + { 1 \over [G : Z(G)] }} .\end{align*}
\todo[inline]{Redo part c}
Group Actions / Representations
Spring 2017 #1
Let \(G\) be a finite group and \(\pi: G\to \operatorname{Sym}^*(G)\) the Cayley representation.
(Recall that this means that for an element \(x\in G\), \(\pi(x)\) acts by left translation on \(G\).)
Prove that \(\pi(x)\) is an odd permutation \(\iff\) the order \({\left\lvert {\pi(x)} \right\rvert}\) of \(\pi(x)\) is even and \({\left\lvert {G} \right\rvert} / {\left\lvert {\pi(x)} \right\rvert}\) is odd.
(DZG): This seems like an unusually hard group theory problem. My guess is this year’s qual class spent more time than usual on the proof of Cayley’s theorem.
- \(\operatorname{Sym}(G) \coloneqq\mathop{\mathrm{Aut}}_{\mathsf{Set}}(G, G)\) is the group of set morphisms from \(G\) to itself, i.e. permutations of elements of \(G\).
-
More standard terminology: this is related to the left regular representation where \(g\mapsto \phi_g\) where \(\phi_g(x) = gx\), regarded instead as a permutation representation.
- This action is transitive!
- Cayley’s theorem: every \(G\) is isomorphic to a subgroup of a permutation group. In particular, take \(\left\{{ \phi_g {~\mathrel{\Big\vert}~}G\in G }\right\}\) with function composition as a subgroup of \(\mathop{\mathrm{Aut}}_{\mathsf{Set}}(G)\).
(DZG): Warning!! I haven’t checked this solution very carefully, and this is kind of a delicate parity argument. Most of the key ideas are borrowed from here.
- Write \(k \coloneqq o(\pi_g)\), then since \(\pi\) is injective, \(k = o(g)\) in \(G\).
- Since \(\pi_g\) as a cycle is obtained from the action of \(g\), we can pick an element \(x_0\) in \(G\), take the orbit under the action, and obtain a cycle of length \(k\) since the order of \(g\) is \(k\). Then continue by taking any \(x_1\) not in the first orbit and taking its orbit. Continuing this way exhausts all group elements and yields a decomposition into disjoint cycles: \begin{align*} \pi_g = (x_0, gx_0, g^2 x_0, \cdots, g^{k-1} x_0) (x_1, gx_1, g^2 x_1, \cdots, g^{k-1} x_1) \cdots (x_m, gx_m, g^2 x_m, \cdots, g^{k-1} x_m) .\end{align*}
- So there are \(m\) orbits all of length exactly \(k\). Proceed by casework.
-
If \(k\) is even:
- This yields \(m\) odd cycles, and thus \(\pi\) has zero (an even number) of even cycles.
- Thus \(\pi \in \ker \operatorname{sgn}\) and is an even permutation.
-
If \(k\) is odd
- This yields \(m\) even cycles, thus an even number of even cycles iff \(m\) is even
-
The claim is that the number of orbit representatives \(m\) is equal to \([G:H] = {\sharp}G/H\) for \(H = \left\langle{ g }\right\rangle\).
- Proof: define a map \begin{align*} \left\{{ \text{Orbit representatives } x_i }\right\} &\to G/H \\ x &\mapsto xH .\end{align*}
- This is injective and surjective because \begin{align*} xH = yH &\iff xy^{-1}\in H = \left\langle{ g }\right\rangle \\ &\iff xy^{-1}= g^\ell \\ &\iff x=g^\ell y \\ &\iff y\in {\mathcal{O}}_x ,\end{align*} so \(y\) and \(x\) are in the same orbit and have the same orbit representative.
- We now have \begin{align*} \pi_g \text{ is an even permutation } \iff \begin{cases} k \text{ is odd and } m \text{ is even} & \\ \text{ or } & \\ k \text{ is even} & . \end{cases} \end{align*}
- Everything was an iff, so flip the evens to odds: \begin{align*} \pi_g \text{ is an odd permutation } \iff \begin{cases} k \text{ is even and } m \text{ is odd} & \\ \text{ or } & \\ k \text{ is odd} & . \end{cases} .\end{align*}
- Then just recall that \(k\coloneqq o(\pi_g)\) and \begin{align*} m= [G: \left\langle{ g }\right\rangle] = {\sharp}G / {\sharp}\left\langle{ g }\right\rangle= {\sharp}G / o(g) = {\sharp}G/ o(\pi_g) .\end{align*}
Fall 2015 #1
Let \(G\) be a group containing a subgroup \(H\) not equal to \(G\) of finite index. Prove that \(G\) has a normal subgroup which is contained in every conjugate of \(H\) which is of finite index.
(DZG) A remark: it’s not the conjugates that should be finite index here, but rather the normal subgroup.
- Let \(H\leq G\) and define \(n\coloneqq[G:H]\).
- Write \(G/H = \left\{{ x_1 H, \cdots, x_n H }\right\}\) for the finitely many cosets.
- Let \(G\) act on \(G/H\) by left translation, so \(g\cdot xH \coloneqq gxH\).. Call the action \(\psi: G\to \operatorname{Sym}(G/H)\).
- Then \({\operatorname{Stab}}(xH) = xHx^{-1}\) is a subgroup conjugate to \(H\), and \(K\coloneqq\ker \psi = \bigcap_{i=1}^n xHx^{-1}\) is the intersection of all conjugates of \(H\).
- Kernels are normal, so \(K{~\trianglelefteq~}G\), and \(K\subseteq xHx^{-1}\) for all \(x\), meaning \(K\) is contained in every conjugate of \(H\).
- The index \([G:K]\) is finite since \(G/K \cong \operatorname{im}\psi\) by the first isomorphism theorem, and \({\sharp}\operatorname{im}\psi \leq {\sharp}\operatorname{Sym}(G/H) = {\sharp}S_n = n! < \infty\).
Conjugacy Classes
Spring 2021 #2
Let \(H {~\trianglelefteq~}G\) be a normal subgroup of a finite group \(G\), where the order of \(H\) is the smallest prime \(p\) dividing \({\left\lvert {G} \right\rvert}\). Prove that \(H\) is contained in the center of \(G\).
Solution due to Swaroop Hegde, typed up + modifications added by DZG.
- \(x\in Z(G)\) iff \({\sharp}C_x = 1\), i.e. the size of its conjugacy class is one.
-
Normal subgroups are disjoint unions of (some) conjugacy classes in \(G\).
- In fact, this is a characterization of normal subgroups (i.e. \(H\) is normal iff \(H\) is a union of conjugacy classes in \(G\)).
- Why: if \(H{~\trianglelefteq~}G\) then \(ghg^{-1}\in H\) for all \(g\), so \(C_h \subseteq H\) and \(\bigcup_h C_h = H\). Conversely, if \(H = \bigcup_{h\in H} C_h\), then \(ghg^{-1}\in C_h \subseteq H\) and thus \(gHg^{-1}= H\).
-
Orbit stabilizer theorem: \({\sharp}C_g = {\sharp}G/ {\sharp}K_g\) where \(C_g\) is the centralizer and \(K_g\) is the conjugacy class of \(g\).
- In particular, \({\sharp}C_g\) divides \({\sharp}G\).
Show an element \(x\) is central by showing \({\sharp}C_x = 1\).
-
Let \(p \coloneqq{\sharp}H\).
-
Let \(\left\{{ C_i }\right\}_{i\leq n}\) be the conjugacy classes in \(G\), then \(G = {\textstyle\coprod}_{i\leq n} C_i\)
-
By the first fact, there is a sub-collection \(\left\{{ C_{i_j}}\right\}_{j\leq k }\) such that \begin{align*} H = {\textstyle\coprod}_{j\leq k} C_{i_j} .\end{align*}
-
The identity is always in a single conjugacy class, so \(C_e = \left\{{ e }\right\}\).
-
Since \(e\in H\), without loss of generality, label \(C_{i_1} = \left\{{ e }\right\}\).
-
So \begin{align*} H = \coprod_{j\leq k} C_{i_j} = C_{i_1}{\textstyle \coprod} \displaystyle\coprod_{\substack{ j\leq k \\ j\neq 1} } C_{i_j} .\end{align*}
-
Take cardinality in the above equation \begin{align*} p = 1 + \sum_{\substack{ j\leq k \\ j\neq 1 }} {\sharp}C_{i_j} .\end{align*}
-
So \({\sharp}C_{i_j} \leq p-1\) for all \(j\neq 1\).
-
Every \({\sharp}C_{i_j}\) divides \({\sharp}G\), but \(p\) was the minimal prime dividing \({\sharp}G\), forcing \({\sharp}C_{i_j} = 1\) for all \(j \neq 1\).
- This rules out \({\sharp}C_{i_j}\) being a prime less than \(p\), but also rules out composites: if a prime \(q\divides {\sharp}C_{i_j}\), then \(q<p\) and \(q\divides {\sharp}G\), a contradiction.
-
By fact 3, each \(x\in C_{i_j}\) satisfies \(x\in Z(G)\).
-
\(\cup C_{i_j} = H\), so \(H \subseteq Z(G)\).
Spring 2015 #1
For a prime \(p\), let \(G\) be a finite \(p{\hbox{-}}\)group and let \(N\) be a normal subgroup of \(G\) of order \(p\). Prove that \(N\) is contained in the center of \(G\).
- Definition of conjugacy class: \([x] = \left\{{gxg^{-1}{~\mathrel{\Big\vert}~}g\in G}\right\}\).
- A conjugacy class \([x]\) is trivial iff \([x] = \left\{{ x }\right\}\) iff \(x\in Z(G)\).
-
Sizes of conjugacy classes divide the order of the group they live in.
- This is orbit-stabilizer: \(G\curvearrowright G\) by \(g\cdot x \coloneqq gxg^{-1}\), so \({\mathcal{O}}(x) = [x]\). Then \({\sharp}{\mathcal{O}}(x) = {\sharp}G / {\sharp}{\operatorname{Stab}}(x)\), so \({\sharp}{\mathcal{O}}(x)\) divides \({\sharp}G\).
- Use that \(N{~\trianglelefteq~}G \iff N = {\textstyle\coprod}' [n_i]\) is a disjoint union of (full) conjugacy classes.
- Take cardinalities: \begin{align*} p = {\sharp}N = \sum_{i=1}^m {\sharp}[n_i] = 1 + \sum_{i=2}^m [n_i] .\end{align*}
- The size of each conjugacy class divides the size of \(H\) by orbit-stabilizer, so \({\sharp}[n_i] \divides p\) for each \(i\).
- But the entire second term must sum to \(p-1\) for this equality to hold, which forces \({\sharp}[n_i] = 1\) (and incidentally \(m=p-1\))
- Then \([n_i] = \left\{{ n_i }\right\} \iff n_i \in Z(G)\), and this holds for all \(i\), so \(N \subseteq Z(G)\).
Unsorted / Counting Arguments
Fall 2021 #2
Give generators and relations for the non-commutative group \(G\) of order 63 containing an element of order \(9 .\)
-
Idea: take a semidirect product involving \(C_9\) and \(C_7\). We’ll need some facts: \(\mathop{\mathrm{Hom}}(C_m, C_n) \cong C_d\) where \(d = \gcd(m, n)\), and \(\mathop{\mathrm{Aut}}(C_m)\cong C_m^{\times}\) which has order \(\phi(m)\) (since one needs to send generators to generators), which can be explicitly calculated based on the prime factorization of \(m\).
-
Some calculations we’ll need:
- \(\mathop{\mathrm{Aut}}(C_9) \cong C_9^{\times}\cong C_{\phi(9)} \cong C_6\), using that \(\phi(p^k) = p^{k-1}(p-1)\).
- \(\mathop{\mathrm{Aut}}(C_7) \cong C_7^{\times}\cong C_{\phi(7)}\cong C_6\) using that \(\phi(p) = p-1\).
-
To get a nonabelian group, we need a nontrivial semidirect product, so look at \(\mathop{\mathrm{Hom}}(G, \mathop{\mathrm{Aut}}(H))\) in the two possible combinations.
- \(\mathop{\mathrm{Hom}}(C_7, \mathop{\mathrm{Aut}}(C_9)) \cong \mathop{\mathrm{Hom}}(C_7, C_6) \cong C_1 \coloneqq\left\{{e}\right\}\) using that \(\mathop{\mathrm{Hom}}(C_m, C_n) \cong C_{d}\) for \(d = \gcd(m, n)\). So there are no nontrivial homs here, so only the direct product is possible.
- \(\mathop{\mathrm{Hom}}(C_9, \mathop{\mathrm{Aut}}(C_7)) \cong \mathop{\mathrm{Hom}}(C_9, C_6) \cong C_3\), so use this!
- Note that we don’t have to consider possibilities for \(C_3\times C_3\), since including this as a factor would yield no elements of order 9.
-
So take \(G\coloneqq C_7 \rtimes_\psi C_9\) for some \(\psi: C_9 \to \mathop{\mathrm{Aut}}(C_7)\), and we can take the presentation \begin{align*} G = \left\langle{x, y{~\mathrel{\Big\vert}~}x^7, y^9, yxy^{-1}= \psi(x)}\right\rangle .\end{align*}
-
It now suffices to find a nontrivial \(\psi: C_7\to C_7\). Writing it multiplicatively as \(C_7 = \left\langle{x{~\mathrel{\Big\vert}~}x^7}\right\rangle\), any map that sends \(x\) to a generator will do. It suffices to choose any \(k\) coprime to \(7\), and then take \(\psi(x) \coloneqq x^k\), which will be another generator.
-
So take
\begin{align*} G = \left\langle{x, y{~\mathrel{\Big\vert}~}x^7, y^9, yxy^{-1}= x^2}\right\rangle .\end{align*}
Fall 2019 Midterm #5
Let \(G\) be a nonabelian group of order \(p^3\) for \(p\) prime. Show that \(Z(G) = [G, G]\).
Note: this is a good problem, it tests several common theorems at once. Proof due to Paco Adajar.
Important notations and definitions:
-
The center of \(G\), denoted by \(Z(G)\), is the subset of elements of \(G\) which commute with all elements of \(G\). That is, if \(x \in Z(G)\), then for all \(g \in G\), \(gx = xg\): \begin{align*}Z(G) = \{ x \in G : gx = xg \, \text{for all } g \in G \}.\end{align*}
In fact, \(Z(G)\) is not just a subset of \(G\), but a normal subgroup of \(G\).
-
The commutator subgroup of \(G\), denoted by \([G, G]\), is the subgroup of \(G\) generated by the commutators of \(G\), i.e., the elements of the form \(ghg^{-1}h^{-1}\): \begin{align*}[G, G] = \langle ghg^{-1}h^{-1} : g, h \in G \rangle.\end{align*}
The commutator subgroup \([G,G]\) is the smallest normal subgroup of \(G\) whose quotient is abelian. That is, if \(H\) is a normal subgroup of \(G\) for which \(G/H\) is abelian, then \([G, G] \le H\).
Moreover, \(G\) is abelian if and only if \([G,G]\) is trivial.
Theorems to remember and know how to prove:
-
\(G/Z(G)\) Theorem: If \(G/Z(G)\) is cyclic, then \(G\) is abelian, i.e., \(G/Z(G)\) is in fact trivial.
-
Lagrange’s Theorem: If \(G\) is a group of finite order and \(H\) is a subgroup of \(G\), then the order of \(H\) divides that of \(G\).
- One consequence of this is that every group of prime order is cyclic.
-
A \(p\)-group (a group of order \(p^n\) for some prime \(p\) and some positive integer \(n\)) has nontrivial center.
-
A consequence of the theorems above: every group of order \(p^2\) (where \(p\) is prime) is abelian.
Since \(Z(G)\) is a subgroup of \(G\) and \(|G| = p^3\), by Lagrange’s theorem, \(|Z(G)| \in \{1, p, p^2, p^3\}\).
Since we stipulated that \(G\) is nonabelian, \(|Z(G)| \ne p^3\). Also, since \(G\) is a \(p\)-group, it has nontrivial center, so \(|Z(G)| \ne 1\). Finally, by the \(G/Z(G)\) theorem, \(|Z(G)| \ne p^2\): if \(|Z(G)| = p^2\), then \(|G/Z(G)| = p\) and so \(G/Z(G)\) would be cyclic, meaning that \(G\) is abelian. Hence, \(|Z(G)| = p\).
Then, since \(|Z(G)| = p\), we have that \(|G/Z(G)| = p^2\), and so \(G/Z(G)\) is abelian. Thus, \([G, G] \in Z(G)\). Since \(|Z(G)| = p\), then \(|[G,G]| \in \{ 1, p\}\) again by Lagrange’s theorem. If \(|[G,G]| = p\) then \([G,G] = Z(G)\) and we are done. And, indeed, we must have \(|[G,G]| = p\), because \(G\) is nonabelian and so \(|[G,G]| \ne 1\).
Spring 2012 #2
Let \(G\) be a finite group and \(p\) a prime number such that there is a normal subgroup \(H{~\trianglelefteq~}G\) with \({\left\lvert {H} \right\rvert} = p^i > 1\).
-
Show that \(H\) is a subgroup of any Sylow \(p{\hbox{-}}\)subgroup of \(G\).
-
Show that \(G\) contains a nonzero abelian normal subgroup of order divisible by \(p\).
- \(p\) groups have nontrivial centers.
- Definition of maximality and \(p{\hbox{-}}\)groups
- Sylows are conjugate
- \(Z(G) \operatorname{ch}G\) always.
- Transitivity of characteristic: \(A \operatorname{ch}B\) and \(B{~\trianglelefteq~}C\) implies \(A {~\trianglelefteq~}C\).
Just use maximality for (a). For (b), centers are always abelian, so \(Z(H)\) is good to consider, just need to ensure it’s normal in \(G\). Use transitivity of characteristic.
- By definition, \(S\in {\operatorname{Syl}}_p(G) \iff S\) is a maximal \(p{\hbox{-}}\)subgroup: \(S<G\) is a \(p{\hbox{-}}\)group, so \({\sharp}S = p^k\) for some \(k\), \(S\) is a proper subgroup, and \(S\) is maximal in the sense that there are no proper \(p{\hbox{-}}\)subgroups \(S'\) with \(S \subseteq S' \subseteq G\).
- Since \({\sharp}H = p^i\), \(H\) is a \(p{\hbox{-}}\)subgroup of \(G\).
- If \(H\) is maximal, then by definition \(H\in {\operatorname{Syl}}_p(G)\)
-
Otherwise, if \(H\) is not maximal, there exists an \(H' \supseteq H\) with \(H'\leq G\) a \(p{\hbox{-}}\)subgroup properly containing \(H\).
- In this apply the same argument to \(H'\): this yields a proper superset containment at every stage, and since \(G\) is finite, there is no infinite ascending chain of proper supersets.
- So this terminates in some maximal \(p{\hbox{-}}\)subgroup \(S\), i.e. a Sylow \(p{\hbox{-}}\)subgroup.
- So \(H \subseteq S\) for some \(S\in {\operatorname{Syl}}_p(G)\).
- All Sylows are conjugate, so for any \(S' \in {\operatorname{Syl}}_p(G)\) we can write \(S' = gSg^{-1}\) for some \(g\).
- Then using that \(H\) is normal, \(H \subseteq S \implies H = gHg^{-1}\subseteq gSg^{-1}\coloneqq S'\). So \(H\) is contained in every Sylow \(p{\hbox{-}}\)subgroup.
-
Claim: \(Z(H) \leq H\) works.
- It is nontrivial since \(H\) is a \(p{\hbox{-}}\)group and \(p{\hbox{-}}\)groups have nontrivial centers
- It is abelian since \(Z(Z(H)) = Z(H)\).
- \({\sharp}Z(H) = p^\ell\) for some \(\ell \leq i\) by Lagrange
- It thus remains to show that \(Z(H) {~\trianglelefteq~}G\).
- Use that \(Z(H) \operatorname{ch}H\) and use transitivity of characteristic to conclude \(Z(H) {~\trianglelefteq~}H\).
- That \(Z(H) \operatorname{ch}H\): let \(\psi \in \mathop{\mathrm{Aut}}(H)\) and \(x=\psi(y)\in \psi(Z(H))\) so \(y\in Z(H)\), then for arbitrary \(h\in H\), \begin{align*} \psi(y)h &= \psi(y) (\psi \circ \psi^{-1})(h) \\ &= \psi( y \cdot \psi^{-1}(h) ) \\ &= \psi( \psi^{-1}(h) \cdot y ) && \text{since } \psi^{-1}(h)\in H, \, y\in Z(H) \\ &= h\psi(y) .\end{align*}
-
That \(A \operatorname{ch}B {~\trianglelefteq~}C \implies A{~\trianglelefteq~}C\):
- \(A\operatorname{ch}B\) iff \(A\) is fixed by every \(\psi\in \mathop{\mathrm{Aut}}(B)\)., WTS \(cAc^{-1}= A\) for all \(c\in C\).
- Since \(B{~\trianglelefteq~}C\), the automorphism \(\psi({-}) \coloneqq c({-})c^{-1}\) descends to an element of \(\mathop{\mathrm{Aut}}(B)\).
- Then \(\psi(A) = A\) since \(A\operatorname{ch}B\), so \(cAc^{-1}= A\) and \(A{~\trianglelefteq~}C\).
Fall 2016 #1
Let \(G\) be a finite group and \(s, t\in G\) be two distinct elements of order 2. Show that subgroup of \(G\) generated by \(s\) and \(t\) is a dihedral group.
Recall that the dihedral groups of order \(2m\) for \(m\geq 2\) are of the form \begin{align*} D_{2m} = \left\langle{\sigma, \tau {~\mathrel{\Big\vert}~}\sigma^m = 1 = \tau^2, \tau \sigma = \sigma^{-1}\tau}\right\rangle .\end{align*}
-
Suppose \(G = \left\langle{ a, b}\right\rangle\) with \(a^2 = b^2 = e\), satisfying some unknown relations.
-
Consider \(ab\). Since \(G\) is finite, this has finite order, so \((ab)^n = e\) for some \(n\geq 2\).
-
Note \(\left\langle{ab, b}\right\rangle \subseteq \left\langle{a, b}\right\rangle\), since any finite word in \(ab, b\) is also a finite word in \(a, b\).
-
Since \((ab)b = ab^2 = a\), we have \(\left\langle{ab, b}\right\rangle \subseteq \left\langle{a, b}\right\rangle\), so \(\left\langle{ab, b}\right\rangle = \left\langle{a, b}\right\rangle\).
-
Write \(D_{2n} = F(r, s) / \ker \pi\) for \(\pi: F(r, s)\to D_{2n}\) the canonical presentation map.
-
Define \begin{align*} \psi: F(r, s) &\to G \\ r &\mapsto ab \\ t &\mapsto b .\end{align*}
-
This is clearly surjective since it hits all generators.
-
We’ll show that \(ab, a\) satisfy all of the relations defining \(D_{2n}\), which factors \(\psi\) through \(\ker \pi\), yielding a surjection \(\tilde \psi: D_{2n} \twoheadrightarrow G\).
- \((ab)^n = e\) by construction, \(b^2 = e\) by assumption, and \begin{align*} b (ab) b^{-1}= babb^{-1}= ba = b^{-1}a^{-1}= (ab)^{-1} ,\end{align*} corresponding to the relation \(srs^{-1}= r^{-1}\). Here we’ve used that \(o(a) = o(b) = 2\) implies \(a=a^{-1}, b=b^{-1}\).
-
Surjectivity of \(\tilde \psi\) yields \(2n = {\sharp}D_{2n} \geq {\sharp}G\).
-
The claim is that \({\sharp}G \geq 2n\), which forces \({\sharp}G = 2n\). Then \(\tilde \psi\) will be a surjective group morphism between groups of the same order, and thus an isomorphism.
- We have \(\left\langle{ ab }\right\rangle\leq G\), so \(n\divides {\sharp}G\).
- Since \(b\not\in \left\langle{ ab }\right\rangle\), this forces \({\sharp}G > n\), so \({\sharp}G \geq 2n\).
Remark: see a more direct proof in Theorem 2.1 and Theorem 1.1 here
Fall 2019 Midterm #1
Let \(G\) be a group of order \(p^2q\) for \(p, q\) prime. Show that \(G\) has a nontrivial normal subgroup.
:::
-
Write \({\sharp}G = p^2 q\)
-
Cases: first assume \(p>q\), then do \(q<p\).
-
In any case, we have \begin{align*} n_p \divides q &\implies n_p \in \left\{{ 1,q }\right\} \\ \\ n_q \divides p^2 &\implies n_q \in \left\{{ 1, p, p^2}\right\} .\end{align*}
-
If \(n_p=1\) or \(n_q=1\), we’re done, so suppose otherwise.
-
Case 1: \(:p>q\).
- Using that \([n_p]_p \equiv 1\), consider reducing elements in \(\left\{{1, q}\right\} \operatorname{mod}p\).
- Since \(q<p\), we just have \(q\operatorname{mod}p = q\), and as long as \(q\neq 1\) we have \(q\not\equiv 1\operatorname{mod}p\). But since \(n_p\neq 1\) and \(n_p\neq q\), this is a contradiction. \(\contradiction\)
-
Case 2: \(p< q\):
-
Using that \([n_q]_q \equiv 1\), consider reducing \(\left\{{1, p, p^2}\right\}\operatorname{mod}q\).
-
Since now \(p<q\), we have \(p\operatorname{mod}q = p\) itself, so \(p\operatorname{mod}q \neq 1\) and we can rule it out.
-
The remaining possibility is \(n_q = p^2\).
-
Supposing that \(n_p \neq 1\), we have \(n_p=q\), so we can count \begin{align*} \text{Elements from Sylow } q: n_q( {\sharp}S_q - 1) &= p^2(q-1) + 1 ,\end{align*} where we’ve used that distinct Sylow \(q\)s can only intersect at the identity, and although Sylow \(p\)s can intersect trivially, they can also intersect in a subgroup of size \(p\).
-
Suppose all Sylow \(p\)s intersect trivially, we get at least \begin{align*} \text{Elements from Sylow } p: n_p( {\sharp}S_p - 1) &= q(p^2-1) .\end{align*} Then we get a count of how many elements the Sylow \(p\)s and \(q\)s contribute: ` \begin{align*} q(p^2-1) + p^2(q-1) + 1 = p^2q - q + p^2q - p^2 + 1 = p^2q + (p^2-1)(q-1)
p^2q = {\sharp}G ,\end{align*} `{=html} provided \((p^2-1)(q-1) \neq 0\), which is fine for \(p\geq 2\) since this is at least \((2^2-1)(3-2) = 3\) (since \(p<q\) and \(q=3\) is the next smallest prime). \(\contradiction\)
-
Otherwise, we get two Sylow \(p\)s intersecting nontrivially, which must be in a subgroup of order at least \(p\) since the intersection is a subgroup of both. In this case, just considering these two subgroups, we get \begin{align*} \text{Elements from Sylow } p: n_p( {\sharp}S_p - 1) &> p^2 + p^2 - p = 2p^2-p -1 .\end{align*} Then a count: \begin{align*} p^2(q-1) + (2p^2-p - 1) + 1 &= p^2 q- p^2 + 2p^2 -p \\ &= p^2 q + p^2 -p \\ &= p^2q + p(p-1) \\ &> p^2q = {\sharp}G ,\end{align*} a contradiction since this inequality is strict provided \(p\geq 2\). \(\contradiction\)
-
Fall 2019 Midterm #4
Let \(p\) be a prime. Show that \(S_p = \left\langle{\tau, \sigma}\right\rangle\) where \(\tau\) is a transposition and \(\sigma\) is a \(p{\hbox{-}}\)cycle.
Groups: Group Actions
Fall 2012 #1
Let \(G\) be a finite group and \(X\) a set on which \(G\) acts.
-
Let \(x\in X\) and \(G_x \coloneqq\left\{{g\in G {~\mathrel{\Big\vert}~}g\cdot x = x}\right\}\). Show that \(G_x\) is a subgroup of \(G\).
-
Let \(x\in X\) and \(G\cdot x \coloneqq\left\{{g\cdot x {~\mathrel{\Big\vert}~}g\in G}\right\}\). Prove that there is a bijection between elements in \(G\cdot x\) and the left cosets of \(G_x\) in \(G\).
Fall 2015 #2
Let \(G\) be a finite group, \(H\) a \(p{\hbox{-}}\)subgroup, and \(P\) a sylow \(p{\hbox{-}}\)subgroup for \(p\) a prime. Let \(H\) act on the left cosets of \(P\) in \(G\) by left translation.
Prove that this is an orbit under this action of length 1.
Prove that \(xP\) is an orbit of length 1 \(\iff H\) is contained in \(xPx^{-1}\).
Spring 2016 #5
Let \(G\) be a finite group acting on a set \(X\). For \(x\in X\), let \(G_x\) be the stabilizer of \(x\) and \(G\cdot x\) be the orbit of \(x\).
-
Prove that there is a bijection between the left cosets \(G/G_x\) and \(G\cdot x\).
-
Prove that the center of every finite \(p{\hbox{-}}\)group \(G\) is nontrivial by considering that action of \(G\) on \(X=G\) by conjugation.
Fall 2017 #1
Suppose the group \(G\) acts on the set \(A\). Assume this action is faithful (recall that this means that the kernel of the homomorphism from \(G\) to \(\operatorname{Sym}^*(A)\) which gives the action is trivial) and transitive (for all \(a, b\) in \(A\), there exists \(g\) in \(G\) such that \(g \cdot a = b\).)
-
For \(a \in A\), let \(G_a\) denote the stabilizer of \(a\) in \(G\). Prove that for any \(a \in A\), \begin{align*} \bigcap_{\sigma\in G} \sigma G_a \sigma^{-1}= \left\{{1}\right\} .\end{align*}
-
Suppose that \(G\) is abelian. Prove that \(|G| = |A|\). Deduce that every abelian transitive subgroup of \(S_n\) has order \(n\).
Fall 2018 #2
-
Suppose the group \(G\) acts on the set \(X\) . Show that the stabilizers of elements in the same orbit are conjugate.
-
Let \(G\) be a finite group and let \(H\) be a proper subgroup. Show that the union of the conjugates of \(H\) is strictly smaller than \(G\), i.e. \begin{align*} \bigcup_{g\in G} gHg^{-1}\subsetneq G \end{align*}
- Suppose \(G\) is a finite group acting transitively on a set \(S\) with at least 2 elements. Show that there is an element of \(G\) with no fixed points in \(S\).
- Orbit: \(G\cdot x \coloneqq\left\{{g\cdot x {~\mathrel{\Big\vert}~}g\in G}\right\} \subseteq X\)
- Stabilizer: \(G_x \coloneqq\left\{{g\in G{~\mathrel{\Big\vert}~}g\cdot x = x}\right\} \leq G\)
- Orbit-Stabilizer: \(G\cdot x \simeq G/G_x\).
- \(abc\in H \iff b\in a^{-1}H c^{-1}\)
- Set of orbits for \(G\curvearrowright X\), notated \(X/G\).
- Set of fixed points for \(G\curvearrowright X\), notated \(X^g\).
-
Burnside’s Lemma: \({\left\lvert {X/G} \right\rvert} \cdot {\left\lvert {G} \right\rvert} = \sum_{g\in G} {\left\lvert {X^g} \right\rvert}\)
- Number of orbits equals average number of fixed points.
- Fix \(x\), then \(y\in {\mathrm{Orb}}(x) \implies g\cdot x = y\) for some \(g\), and \(x = g^{-1}\cdot y\).
- Then \begin{align*} h \in {\operatorname{Stab}}(x) &\iff h\cdot x = x && \text{by being in the stabilizer} \\ &\iff h\cdot (g^{-1}\cdot y) = g^{-1}\cdot y \\ &\iff (g h g^{-1}) \cdot y = y \\ &\iff ghg^{-1}\in G_y && \text{by definition}\\ &\iff h\in g ^{-1} {\operatorname{Stab}}(y) g ,\end{align*} so \({\operatorname{Stab}}(x) = g^{-1}{\operatorname{Stab}}(y) g\).
Let \(G\) act on its subgroups by conjugation,
-
The orbit \(G\cdot H\) is the set of all subgroups conjugate to \(H\), and
-
The stabilizer of \(H\) is \(G_H = N_G(H)\).
-
By orbit-stabilizer, \begin{align*} G\cdot H = [G: G_H] = [G: N_G(H)] .\end{align*}
-
Since \({\left\lvert {H} \right\rvert} = n\), and all of its conjugate also have order \(n\).
-
Note that \begin{align*} H\leq N_G(H) \implies {\left\lvert {H} \right\rvert} \leq {\left\lvert {N_G(H)} \right\rvert} \implies {1\over {\left\lvert {N_G(H)} \right\rvert}} \leq {1\over {\left\lvert {H} \right\rvert}} ,\end{align*}
-
Now strictly bound the size of the union by overcounting their intersections at the identity: \begin{align*} {\left\lvert {\bigcup_{g\in G}gHg^{-1}} \right\rvert} &< (\text{Number of Conjugates of } H) \cdot (\text{Size of each conjugate}) \\ & \text{strictly overcounts since they intersect in at least the identity} \\ &= [G: N_G(H)] {\left\lvert {H} \right\rvert} \\ &= {{\left\lvert {G} \right\rvert} \over {\left\lvert {N_G(H)} \right\rvert}} {\left\lvert {H} \right\rvert} \\ & \text{since $G$ is finite} \\ &\leq {{\left\lvert {G} \right\rvert} \over {\left\lvert {H} \right\rvert}} {\left\lvert {H} \right\rvert} \\ &= {\left\lvert {G} \right\rvert} .\end{align*}
- Let \(G\curvearrowright X\) transitively where \({\left\lvert {X} \right\rvert} \geq 2\).
- An action is transitive iff there is only one orbit, so \({\left\lvert {X/G} \right\rvert} = 1\).
- Apply Burnside’s Lemma \begin{align*} 1 = {\left\lvert {X/G} \right\rvert} = \frac{1}{{\left\lvert {G} \right\rvert}} \sum_{g\in G} {\left\lvert { \mathrm{Fix}(g)} \right\rvert} \implies {\left\lvert {G} \right\rvert} = \sum_{g\in G} {\left\lvert { \mathrm{Fix}(g)} \right\rvert} = \mathrm{Fix}(e) + \sum_{\substack{g\in G \\ g\neq e}} {\left\lvert { \mathrm{Fix}(g)} \right\rvert} \end{align*}
- Note that \(\mathrm{Fix}(e) = X\), since the identity must fix every element, so \({\left\lvert { \mathrm{Fix}(e)} \right\rvert} \geq 2\).
- If \({\left\lvert { \mathrm{Fix}(g)} \right\rvert} > 0\) for all \(g\neq e\), the remaining term is at least \({\left\lvert {G} \right\rvert} -1\). But then the right-hand side yields is at least \(2 + ({\left\lvert {G} \right\rvert} -1) = {\left\lvert {G} \right\rvert} + 1\), contradicting the equality.
- So not every \({\left\lvert { \mathrm{Fix}(g)} \right\rvert} > 0\), and \({\left\lvert { \mathrm{Fix}(g) } \right\rvert} = 0\) for some \(g\), which says \(g\) has no fixed points in \(X\).
Groups: Sylow Theory
Fall 2019 #1
Let \(G\) be a finite group with \(n\) distinct conjugacy classes. Let \(g_1 \cdots g_n\) be representatives of the conjugacy classes of \(G\). Prove that if \(g_i g_j = g_j g_i\) for all \(i, j\) then \(G\) is abelian.
-
\(Z(g) = G \iff g\in Z(G)\), i.e. if the centralizer of \(g\) is the whole group, \(g\) is central.
-
If \(H\leq G\) is a proper subgroup, then \(\bigcup_{g\in G} hGh^{-1}\) is again a proper subgroup (subset?) I.e. \(G\) is not a union of conjugates of any proper subgroup.
-
So if \(G\) is a union of conjugates of \(H\), then \(H\) must not be proper, i.e. \(H= G\).
- We have \(g_j \subseteq Z(g_k)\) for all \(k\) by assumption.
-
If we can show \(Z(g_k) = G\) for all \(k\), then \(g_k \in Z(G)\) for all \(k\).
- Then each conjugacy class is size 1, and since \(G = {\textstyle\coprod}_{i=1}^n [g_i] = {\textstyle\coprod}_{i=1}^n \left\{{g_i}\right\}\), every \(g\in G\) is some \(g_i\). So \(G \subseteq Z(G)\), forcing \(G\) to be abelian.
-
If we can show \(G \subseteq \bigcup_{h\in H} h Z(g_k) h^{-1}\) for some \(k\), this forces \(Z(g_k) = G\) and \(g_k \in Z(G)\).
- If we can do this for all \(k\), we’re done!
- Since \(g\in G\) is in some conjugacy class, write \(g=hg_j h^{-1}\) for some \(h\in G\) and some \(1\leq j\leq n\).
-
Now use \(g_j \in Z(g_k)\) for all \(k\):
\begin{align*}
g\in G &\implies g = hg_j h^{-1}&& \text{for some } h\in H \\
g_j \in Z(g_k) \forall k &\implies g\in hZ(g_k)h^{-1}&&\text{for some }h, \, \forall 1\leq k \leq n \\
&\implies g\in \bigcup_{h\in G} h Z(g_k) h^{-1}
&&\forall 1\leq k \leq n \\
.\end{align*}
- Note that it’s necessary to get rid of the \(h\) dependence, since now now every \(g\in G\) is in \(\bigcup_{h\in G} hZ(g_k)h^{-1}\).
- Now \begin{align*} G \subseteq \bigcup_{h\in G} hZ(g_k) \subseteq G \,\,\forall k \implies Z(g_k) = G\,\, \forall k ,\end{align*} and we’re done.
Fall 2019 Midterm #2
Let \(G\) be a finite group and let \(P\) be a sylow \(p{\hbox{-}}\)subgroup for \(p\) prime. Show that \(N(N(P)) = N(P)\) where \(N\) is the normalizer in \(G\).
Fall 2013 #2
Let \(G\) be a group of order 30.
-
Show that \(G\) has a subgroup of order 15.
-
Show that every group of order 15 is cyclic.
-
Show that \(G\) is isomorphic to some semidirect product \({\mathbf{Z}}_{15} \rtimes{\mathbf{Z}}_2\).
-
Exhibit three nonisomorphic groups of order 30 and prove that they are not isomorphic. You are not required to use your answer to (c).
Spring 2014 #2
Let \(G\subset S_9\) be a Sylow-3 subgroup of the symmetric group on 9 letters.
-
Show that \(G\) contains a subgroup \(H\) isomorphic to \({\mathbf{Z}}_3 \times{\mathbf{Z}}_3 \times{\mathbf{Z}}_3\) by exhibiting an appropriate set of cycles.
-
Show that \(H\) is normal in \(G\).
-
Give generators and relations for \(G\) as an abstract group, such that all generators have order 3. Also exhibit elements of \(S_9\) in cycle notation corresponding to these generators.
-
Without appealing to the previous parts of the problem, show that \(G\) contains an element of order 9.
Fall 2014 #2
Let \(G\) be a group of order 96.
-
Show that \(G\) has either one or three 2-Sylow subgroups.
-
Show that either \(G\) has a normal subgroup of order 32, or a normal subgroup of order 16.
Spring 2016 #3
-
State the three Sylow theorems.
-
Prove that any group of order 1225 is abelian.
- Write down exactly one representative in each isomorphism class of abelian groups of order 1225.
Spring 2017 #2
-
How many isomorphism classes of abelian groups of order 56 are there? Give a representative for one of each class.
-
Prove that if \(G\) is a group of order 56, then either the Sylow-2 subgroup or the Sylow-7 subgroup is normal.
- Give two non-isomorphic groups of order 56 where the Sylow-7 subgroup is normal and the Sylow-2 subgroup is not normal. Justify that these two groups are not isomorphic.
Fall 2017 #2
-
Classify the abelian groups of order 36.
For the rest of the problem, assume that \(G\) is a non-abelian group of order 36. You may assume that the only subgroup of order 12 in \(S_4\) is \(A_4\) and that \(A_4\) has no subgroup of order 6.
-
Prove that if the 2-Sylow subgroup of \(G\) is normal, \(G\) has a normal subgroup \(N\) such that \(G/N\) is isomorphic to \(A_4\).
-
Show that if \(G\) has a normal subgroup \(N\) such that \(G/N\) is isomorphic to \(A_4\) and a subgroup \(H\) isomorphic to \(A_4\) it must be the direct product of \(N\) and \(H\).
-
Show that the dihedral group of order 36 is a non-abelian group of order 36 whose Sylow-2 subgroup is not normal.
Fall 2012 #2
Let \(G\) be a group of order 30.
-
Show that \(G\) contains normal subgroups of orders 3, 5, and 15.
-
Give all possible presentations and relations for \(G\).
- Determine how many groups of order 30 there are up to isomorphism.
Fall 2018 #1
Let \(G\) be a finite group whose order is divisible by a prime number \(p\). Let \(P\) be a normal \(p{\hbox{-}}\)subgroup of \(G\) (so \({\left\lvert {P} \right\rvert} = p^c\) for some \(c\)).
-
Show that \(P\) is contained in every Sylow \(p{\hbox{-}}\)subgroup of \(G\).
-
Let \(M\) be a maximal proper subgroup of \(G\). Show that either \(P \subseteq M\) or \(|G/M | = p^b\) for some \(b \leq c\).
- Sylow 2: All Sylow \(p{\hbox{-}}\)subgroups are conjugate.
- \({\left\lvert {HK} \right\rvert} = {\left\lvert {H} \right\rvert} {\left\lvert {K} \right\rvert} / {\left\lvert {H\cap K} \right\rvert}\).
- Lagrange’s Theorem: \(H\leq G \implies {\left\lvert {H} \right\rvert} \divides {\left\lvert {G} \right\rvert}\)
-
Every \(p{\hbox{-}}\)subgroup is contained in some Sylow \(p{\hbox{-}}\)subgroup, so \(P \subseteq S_p^i\) for some \(S_p^i \in \mathrm{Syl}_p(G)\).
-
\(P {~\trianglelefteq~}G \iff gPg^{-1}= P\) for all \(g\in G\).
-
Let \(S_p^j\) be any other Sylow \(p{\hbox{-}}\)subgroup,
-
Since Sylow \(p{\hbox{-}}\)subgroups are all conjugate \(gS_p^i g^{-1}= S_p^j\) for some \(g\in G\).
-
Then \begin{align*} P = gPg^{-1}\subseteq gS_p^i g^{-1}= S_p^j .\end{align*}
-
If \(P\) is not contained in \(M\), then \(M < MP\) is a proper subgroup
-
By maximality of \(M\), \(MP = G\)
-
Note that \(M\cap P \leq P\) and \({\left\lvert {P} \right\rvert} = p^c\) implies \({\left\lvert {M\cap P} \right\rvert} = p^a\) for some \(a\leq c\) by Lagrange
-
Then write \begin{align*} G = MP &\iff {\left\lvert {G} \right\rvert} = \frac{{\left\lvert {M} \right\rvert} {\left\lvert {P} \right\rvert}}{{\left\lvert {M\cap P} \right\rvert}} \\ \\ &\iff { {\left\lvert {G} \right\rvert} \over {\left\lvert {M} \right\rvert}} = {{\left\lvert {P} \right\rvert} \over {\left\lvert {M\cap P} \right\rvert}} = {p^c \over p^a} = p^{c-a} \coloneqq p^b \end{align*}
where \(a\leq c \implies 0 \leq c-b \leq c\) so \(0\leq b \leq c\).
Fall 2019 #2
Let \(G\) be a group of order 105 and let \(P, Q, R\) be Sylow 3, 5, 7 subgroups respectively.
-
Prove that at least one of \(Q\) and \(R\) is normal in \(G\).
-
Prove that \(G\) has a cyclic subgroup of order 35.
-
Prove that both \(Q\) and \(R\) are normal in \(G\).
-
Prove that if \(P\) is normal in \(G\) then \(G\) is cyclic.
-
The \(pqr\) theorem.
-
Sylow 3: \({\left\lvert {G} \right\rvert} = p^n m\) implies \(n_p \divides m\) and \(n_p \cong 1 \operatorname{mod}p\).
-
Theorem: If \(H, K \leq G\) and any of the following conditions hold, \(HK\) is a subgroup:
- \(H{~\trianglelefteq~}G\) (wlog)
- \([H, K] = 1\)
- \(H \leq N_G(K)\)
-
Theorem: For a positive integer \(n\), all groups of order \(n\) are cyclic \(\iff n\) is squarefree and, for each pair of distinct primes \(p\) and \(q\) dividing \(n\), \(q - 1 \neq 0 \operatorname{mod}p\).
-
Theorem: \begin{align*} A_i{~\trianglelefteq~}G, \quad G = A_1 \cdots A_k,\quad A_k \cap\prod_{i\neq k} A_i = \emptyset \implies G = \prod A_i .\end{align*}
-
The intersection of subgroups is a again a subgroup.
-
Any subgroups of coprime order intersect trivially?
-
We have
-
\(n_3 \divides 5\cdot 7, \quad n_3 \cong 1 \operatorname{mod}3 \implies n_3 \in \left\{{1, 5, 7, 35}\right\} \setminus \left\{{5, 35}\right\}\)
-
\(n_5 \divides 3\cdot 7, \quad n_5 \cong 1 \operatorname{mod}5 \implies n_5 \in \left\{{1, 3, 7, 21}\right\}\setminus \left\{{3, 7}\right\}\)
-
\(n_7 \divides 3\cdot 5, \quad n_7 \cong 1 \operatorname{mod}7 \implies n_7 \in \left\{{1, 3, 5, 15}\right\}\setminus\left\{{3, 5}\right\}\)
-
Thus \begin{align*} n_3 \in \left\{{1, 7}\right\} \quad n_5 \in \left\{{1, 21}\right\} \quad n_7 \in \left\{{1, 15}\right\} .\end{align*}
-
Toward a contradiction, if \(n_5\neq 1\) and \(n_7 \neq 1\), then \begin{align*} {\left\lvert {{\operatorname{Syl}}(5) \cup{\operatorname{Syl}}(7)} \right\rvert} = (5-1)n_5 + (7-1)n_7 + 1 &= 4(21) + 6(15) = 174 > 105 \text{ elements} \end{align*} using the fact that Sylow \(p{\hbox{-}}\)subgroups for distinct primes \(p\) intersect trivially (?).
- By (a), either \(Q\) or \(R\) is normal.
- Thus \(QR \leq G\) is a subgroup, and it has order \({\left\lvert {Q} \right\rvert} \cdot {\left\lvert {R} \right\rvert} = 5\cdot 7 = 35\).
- By the \(pqr\) theorem, since \(5\) does not divide \(7-1=6\), \(QR\) is cyclic.
\todo[inline]{Part (b) not finished!}
-
We want to show \(Q, R{~\trianglelefteq~}G\), so we proceed by showing \(\textbf{not }\qty{n_5 = 21 \text{ or } n_7 = 15}\), which is equivalent to \(\qty{n_5 = 1 \text{ and } n_7 = 1}\) by the previous restrictions.
-
Note that we can write \begin{align*} G = \left\{{\text{elements of order } n}\right\} {\textstyle\coprod}\left\{{\text{elements of order not } n}\right\} .\end{align*} for any \(n\), so we count for \(n=5, 7\):
- Elements in \(QR\) of order not equal to 5: \({\left\lvert {QR - Q\left\{{\operatorname{id}}\right\} + \left\{{\operatorname{id}}\right\}} \right\rvert} = 35 - 5 + 1 = 31\)
- Elements in \(QR\) of order not equal to 7: \({\left\lvert {QR - \left\{{\operatorname{id}}\right\}R + \left\{{\operatorname{id}}\right\}} \right\rvert} = 35 - 7 + 1 = 29\)
-
Since \(QR \leq G\), we have
- Elements in \(G\) of order not equal to 5 \(\geq 31\).
- Elements in \(G\) of order not equal to 7 \(\geq 29\).
-
Now both cases lead to contradictions:
-
\(n_5 = 21\): \begin{align*} {\left\lvert {G} \right\rvert} &= {\left\lvert {\left\{{\text{elements of order } 5}\right\} {\textstyle\coprod}\left\{{\text{elements of order not } 5}\right\}} \right\rvert} \\ &\geq n_5(5-1) + 31 = 21(4) + 31 = 115 > 105 = {\left\lvert {G} \right\rvert} .\end{align*}
-
\(n_7 = 15\): \begin{align*} {\left\lvert {G} \right\rvert} &= {\left\lvert {\left\{{\text{elements of order } 7}\right\} {\textstyle\coprod}\left\{{\text{elements of order not } 7}\right\}} \right\rvert} \\ &\geq n_7(7-1) + 29 = 15(6) + 29 = 119 > 105 = {\left\lvert {G} \right\rvert} .\end{align*}
-
Suppose \(P\) is normal and recall \({\left\lvert {P} \right\rvert} = 3, {\left\lvert {Q} \right\rvert} = 5, {\left\lvert {R} \right\rvert} = 7\).
- \(P\cap QR = \left\{{e}\right\}\) since \((3, 35) = 1\)
- \(R\cap PQ = \left\{{e}\right\}\) since \((5, 21) = 1\)
- \(Q\cap RP = \left\{{e}\right\}\) since \((7, 15) = 1\)
We also have \(PQR = G\) since \({\left\lvert {PQR} \right\rvert} = {\left\lvert {G} \right\rvert}\) (???).
We thus have an internal direct product \begin{align*} G \cong P\times Q \times R \cong {\mathbf{Z}}_3 \times{\mathbf{Z}}_5 \times{\mathbf{Z}}_7 \cong {\mathbf{Z}}_{105} .\end{align*} by the Chinese Remainder Theorem, which is cyclic.
Spring 2021 #3
-
Show that every group of order \(p^2\) with \(p\) prime is abelian.
-
State the 3 Sylow theorems.
-
Show that any group of order \(4225 = 5^2 13^2\) is abelian.
-
Write down one representative from each isomorphism class of abelian groups of order 4225.
Fall 2020 #1
-
Using Sylow theory, show that every group of order \(2p\) where \(p\) is prime is not simple.
-
Classify all groups of order \(2p\) and justify your answer. For the nonabelian group(s), give a presentation by generators and relations.
Fall 2020 #2
Let \(G\) be a group of order 60 whose Sylow 3-subgroup is normal.
-
Prove that \(G\) is solvable.
-
Prove that the Sylow 5-subgroup is also normal.
Groups: Classification
Spring 2020 #1
-
Show that any group of order 2020 is solvable.
-
Give (without proof) a classification of all abelian groups of order 2020.
- Describe one nonabelian group of order 2020.
\todo[inline]{Work this problem.}
Spring 2019 #3
How many isomorphism classes are there of groups of order 45?
Describe a representative from each class.
- Sylow theorems:
- \(n_p \cong 1 \operatorname{mod}p\)
- \(n_p \divides m\).
-
It turns out that \(n_3 = 1\) and \(n_5 = 1\), so \(G \cong S_3 \times S_5\) since both subgroups are normal.
-
There is only one possibility for \(S_5\), namely \(S_5\cong {\mathbf{Z}}/(5)\).
-
There are two possibilities for \(S_3\), namely \(S_3 \cong {\mathbf{Z}}/(3^2)\) and \({\mathbf{Z}}/(3)^2\).
-
Thus
-
\(G \cong {\mathbf{Z}}/(9) \times{\mathbf{Z}}/(5)\), or
-
\(G \cong {\mathbf{Z}}/(3)^2 \times{\mathbf{Z}}/(5)\).
\todo[inline]{Revisit, seems short.}
Spring 2012 #3
Let \(G\) be a group of order 70.
-
Show that \(G\) is not simple.
-
Exhibit 3 nonisomorphic groups of order 70 and prove that they are not isomorphic.
Fall 2016 #3
How many groups are there up to isomorphism of order \(pq\) where \(p<q\) are prime integers?
Spring 2018 #1
-
Use the Class Equation (equivalently, the conjugation action of a group on itself) to prove that any \(p{\hbox{-}}\)group (a group whose order is a positive power of a prime integer \(p\)) has a nontrivial center.
-
Prove that any group of order \(p^2\) (where \(p\) is prime) is abelian.
-
Prove that any group of order \(5^2 \cdot 7^2\) is abelian.
-
Write down exactly one representative in each isomorphism class of groups of order \(5^2 \cdot 7^2\).
-
Centralizer: \(C_G(x) = \left\{{g\in G {~\mathrel{\Big\vert}~}[gx] = 1}\right\}\).
-
Class Equation: \({\left\lvert {G} \right\rvert} = {\left\lvert {Z(G)} \right\rvert} + \sum [G: C_G(x_i)]\)
-
\(G/Z(G)\) cyclic \(\iff G\) is abelian. \begin{align*} G/Z(G) = \left\langle{xZ}\right\rangle &\iff g\in G \implies gZ = x^mZ \\ &\iff g(x^m)^{-1}\in Z \\ &\iff g = x^m z {\quad \operatorname{for some} \quad}z\in Z\\ &\implies gh = x^mz_1 x^n z_2 = x^n z_2 x^m z_1 = hg .\end{align*}
-
Every group of order \(p^2\) is abelian.
-
Classification of finite abelian groups.
Strategy: get \(p\) to divide \({\left\lvert {Z(G)} \right\rvert}\).
-
Apply the class equation: \begin{align*} {\left\lvert {G} \right\rvert} = {\left\lvert {Z(G)} \right\rvert} + \sum [G: C_G(x_i)] .\end{align*}
-
Since \(C_G(x_i) \leq G\) and \({\left\lvert {G} \right\rvert} = p^k\), by Lagrange \({\left\lvert {C_G(x_i)} \right\rvert} = p^\ell\) for some \(0\leq \ell \leq k\).
-
Since \({\left\lvert {G} \right\rvert} = p^k\) for some \(k\) and \(Z(G), C_G(x_i) \leq G\) are subgroups, their orders are powers of \(p\).
-
Use \begin{align*}[G: C_G(x_i)] = 1 \iff C_G(x_i) = G \iff \left\{{g\in G{~\mathrel{\Big\vert}~}gx_ig^{-1}= x_i}\right\} = G \iff x_i \in Z(G).\end{align*}
- Thus every index appearing in the sum is greater than 1, and thus equal to \(p^{\ell_i}\) for some \(1\leq \ell_i \leq k\)
- So \(p\) divides every term in the sum
-
Rearrange \begin{align*} {\left\lvert {G} \right\rvert} - \sum [G: C_G(x_i)] = {\left\lvert {Z(G)} \right\rvert} .\end{align*}
-
\(p\) divides both terms on the LHS, so must divide the RHS, so \({\left\lvert {Z(G)} \right\rvert} \geq p\).
Strategy: examine \({\left\lvert {G/Z(G)} \right\rvert}\) by cases.
- \(1\): Then \(G = Z(G)\) and \(G\) is abelian.
- \(p\): Then \(G/Z(G)\) is cyclic so \(G\) is abelian
- \(p^2\): Not possible, since \({\left\lvert {Z(G)} \right\rvert} > 1\) by (a).
-
By Sylow
- \(n_5 \divides 7^2,\quad n_5\cong 1\operatorname{mod}5 \implies n_5\in\left\{{1, 7, 49}\right\}\setminus\left\{{7, 49}\right\} = \left\{{1}\right\} \implies n_5 = 1\)
- \(n_7 \divides 5^2, \quad n_7 \cong 1 \operatorname{mod}7 \implies n_7 \in \left\{{1, 5, 25}\right\}\setminus\left\{{5, 25}\right\} =\left\{{1}\right\} \implies n_7 = 1\)
-
By recognition of direct products, \(G = S_5 \times S_7\)
- By above, \(S_5, S_7{~\trianglelefteq~}G\)
- Check \(S_5\cap S_7 = \left\{{e}\right\}\) since they have coprime order.
- Check \(S_5S_7 = G\) since \({\left\lvert {S_5 S_7} \right\rvert} = 5^2 7^2 = {\left\lvert {G} \right\rvert}\)
-
By (b), \(S_5, S_7\) are abelian since they are groups of order \(p^2\)
-
The direct product of abelian groups is abelian.
- \({\mathbf{Z}}_{5^2} \times{\mathbf{Z}}_{7^2}\)
- \({\mathbf{Z}}_{5}^2 \times{\mathbf{Z}}_{7^2}\)
- \({\mathbf{Z}}_{5^2} \times{\mathbf{Z}}_{7}^2\)
- \({\mathbf{Z}}_{5}^2 \times{\mathbf{Z}}_{7}^2\)
Groups: Simple and Solvable
\(\star\) Fall 2016 #7
-
Define what it means for a group \(G\) to be solvable.
-
Show that every group \(G\) of order 36 is solvable.
Hint: you can use that \(S_4\) is solvable.
Spring 2015 #4
Let \(N\) be a positive integer, and let \(G\) be a finite group of order \(N\).
-
Let \(\operatorname{Sym}^*G\) be the set of all bijections from \(G\to G\) viewed as a group under composition. Note that \(\operatorname{Sym}^*G \cong S_N\). Prove that the Cayley map \begin{align*} C: G&\to \operatorname{Sym}^*G\\ g &\mapsto (x\mapsto gx) \end{align*} is an injective homomorphism.
-
Let \(\Phi: \operatorname{Sym}^*G\to S_N\) be an isomorphism. For \(a\in G\) define \({\varepsilon}(a) \in \left\{{\pm 1}\right\}\) to be the sign of the permutation \(\Phi(C(a))\). Suppose that \(a\) has order \(d\). Prove that \({\varepsilon}(a) = -1 \iff d\) is even and \(N/d\) is odd.
- Suppose \(N> 2\) and \(n\equiv 2 \operatorname{mod}4\). Prove that \(G\) is not simple.
Hint: use part (b).
Spring 2014 #1
Let \(p, n\) be integers such that \(p\) is prime and \(p\) does not divide \(n\). Find a real number \(k = k (p, n)\) such that for every integer \(m\geq k\), every group of order \(p^m n\) is not simple.
Fall 2013 #1
Let \(p, q\) be distinct primes.
-
Let \(\mkern 1.5mu\overline{\mkern-1.5muq\mkern-1.5mu}\mkern 1.5mu \in {\mathbf{Z}}_p\) be the class of \(q\operatorname{mod}p\) and let \(k\) denote the order of \(\mkern 1.5mu\overline{\mkern-1.5muq\mkern-1.5mu}\mkern 1.5mu\) as an element of \({\mathbf{Z}}_p^{\times}\). Prove that no group of order \(pq^k\) is simple.
-
Let \(G\) be a group of order \(pq\), and prove that \(G\) is not simple.
Spring 2013 #4
Define a simple group. Prove that a group of order 56 can not be simple.
Fall 2019 Midterm #3
Show that there exist no simple groups of order 148.
Commutative Algebra
UFDs, PIDs, etc
Spring 2013 #2
-
Define a Euclidean domain.
-
Define a unique factorization domain.
-
Is a Euclidean domain an UFD? Give either a proof or a counterexample with justification.
-
Is a UFD a Euclidean domain? Give either a proof or a counterexample with justification.
-
\(R\) is Euclidean iff it admits a Euclidean algorithm: there is a degree function \(f: R\to {\mathbf{Z}}_{\geq 0}\) such that for all \(a,b\in R\), there exist \(q, r\in R\) such that \(a = bq + r\) where \(f(r) <f(b)\) or \(r=0\).
-
\(R\) is a UFD iff every \(r\in R\) can be written as \(r = u \prod_{i=1}^n p_i\) with \(n\geq 0\), \(u\in R^{\times}\), and \(p_i\) irreducible. This is unique up to associates of the \(p_i\) and reordering.
-
Euclidean implies UFD:
-
Euclidean implies PID:
- If \(I \in \operatorname{Id}(R)\) one can use the degree function to find any \(b \in I\) where \(f(b)\) is minimal.
- Then \(I = \left\langle{b}\right\rangle\), since if \(a\in I\) one can write \(a = bq + r\) and use that \(a-bq \in I \implies r\in I\).
- But by minimality, we can’t have \(f(r)<f(b)\), so \(r=0\) and \(a \divides b\), so \(b\in \left\langle{a}\right\rangle\).
-
PID implies UFD:
- Use that irreducible implies prime in a PID, so every \(x\in R\) has some factorization into finitely many primes.
- Supposing \(x = u_p \prod_{i=1}^m p_i = u_q \prod_{i=1}^n q_i\), use that \(p_1\) divides the LHS and so \(p_1\) divides the RHS. WLOG, \(p_1\divides q_1\), so \(q_1 = u_1 p_1\) for \(u\in R^{\times}\), so \(x = u_q u_1 p_1 \prod_{i=2}^m q_i\) by rewriting a term on the RHS.
- Note that this makes \(p_1, q_1\) associates.
- Continuing up to \(m\), we get \begin{align*} x &= u_p \prod_{i=1}^m p_i \\ &= u_q \prod_{i=1}^m u_i p_i \prod_{k=m+1}^n q_i \\ \implies u_p &= u_q \prod_{i=1}^m u_i \prod_{k=m+1}^n q_i \\ \tilde u &= \prod_{k=m+1}^n q_i ,\end{align*} where we’ve moved all units to the LHS. This makes \(p_i, q_i\) associates for \(i\leq m\).
- But primes aren’t units and the product of nontrivial primes can’t be a unit, so the right-hand side product must be empty.
- So \(m=n\) and all \(p_i, q_i\) are associate, QED.
-
Euclidean implies PID:
-
UFD does not imply Euclidean:
- It suffices to find a UFD that is not a PID.
- Take \(R \coloneqq{\mathbf{C}}[x, y]\), which is a UFD by the usual factorization of polynomials. It is not a PID, since \(\left\langle{2, x}\right\rangle\) is not principal.
Fall 2017 #6
For a ring \(R\), let \(U(R)\) denote the multiplicative group of units in \(R\). Recall that in an integral domain \(R\), \(r \in R\) is called irreducible if \(r\) is not a unit in R, and the only divisors of \(r\) have the form \(ru\) with \(u\) a unit in \(R\).
We call a non-zero, non-unit \(r \in R\) prime in \(R\) if \(r \divides ab \implies r \divides a\) or \(r \divides b\). Consider the ring \(R = \{a + b \sqrt{-5}{~\mathrel{\Big\vert}~}a, b \in Z\}\).
-
Prove \(R\) is an integral domain.
-
Show \(U(R) = \{\pm1\}\).
-
Show \(3, 2 + \sqrt{-5}\), and \(2 - \sqrt{-5}\) are irreducible in \(R\).
-
Show 3 is not prime in \(R\).
- Conclude \(R\) is not a PID.
- Integral domain: \(ab=0 \implies a\neq 0 \text{ or } b\neq 0\).
- Prime: \(p \divides ab \implies p\divides a\) or \(b\).
- Reducible: \(a = xy\) where \(x, y\) are proper divisors.
- Irreducible implies prime in a UFD.
-
\(R\) is an integral domain:
- Let \(\alpha = a + b\sqrt{-5}\) and \(\beta = c + d \sqrt{-5}\) and set \(\mkern 1.5mu\overline{\mkern-1.5mu\alpha\mkern-1.5mu}\mkern 1.5mu, \mkern 1.5mu\overline{\mkern-1.5mu\beta\mkern-1.5mu}\mkern 1.5mu\) be their conjugates.
- Then \begin{align*} 0 = \alpha \beta = \alpha\mkern 1.5mu\overline{\mkern-1.5mu\alpha \mkern-1.5mu}\mkern 1.5mu\beta\mkern 1.5mu\overline{\mkern-1.5mu\beta \mkern-1.5mu}\mkern 1.5mu= (a^2-5b^2)(c^2-5d^2) \in {\mathbf{Z}} ,\end{align*} so one factor is zero.
- If \(a^2 = 5b^2\) then \(a = \sqrt{5} b \not\in {\mathbf{Z}}\) unless \(a=b=0\). Otherwise, the same argument forces \(c=d=0\).
-
The units are \(\pm 1\):
- Use that \(u\in R^{\times}\implies N(u) = \pm 1\), and \(N(\alpha) = \alpha \mkern 1.5mu\overline{\mkern-1.5mu\alpha \mkern-1.5mu}\mkern 1.5mu= (a+b\sqrt{-5})(a-b\sqrt{-5}) = a^2 + 5b^2 = 1\) forces \(b=0\) and \(a=\pm 1\).
-
Irreducible elements:
- \(2, 3\) are irreducible because if (say) \(3=xy\) then \(N(x)N(y) = N(3) = 9\), and if neither \(x,y\) are units then \(N(x) = N(y) = 3\). But \(N(a + b\sqrt{-5}) = a^2 + 5b^2\) and \(a^2 + 5b^2 = 3\) has no solutions. The same argument works for \(2\).
- \(2\pm \sqrt{-5}\) are irreducible because \(N(2 + \sqrt{-5}) = 2^2 + 5(1) = 9\), and in fact \(N(2 - \sqrt{-5}) = 2^2 + 5(-1)^2 = 9\). By the same argument as above, this forces irreducibility.
-
\(3\) is not prime:
- We can write \(6 = (3)(2) = (1 + \sqrt{-5})(1 - \sqrt{-5})\), so if we assume \(3\) is prime we get \(3\divides (1 \pm \sqrt{-5})\).
- But writing \((1\pm \sqrt{-5}) = 3r\) for some \(r\in R\) yields \begin{align*} (1 \pm \sqrt{-5}) = 3(a + b\sqrt{-5}) \implies 3a=1, 3b = \pm 1 .\end{align*} These have no solutions \(a, b\in {\mathbf{Z}}\). \(\contradiction\)
-
\(R\) is not a PID:
- Use that irreducibles are prime in a UFD, which is not true here.
Spring 2017 #4
-
Let \(R\) be an integral domain with quotient field \(F\). Suppose that \(p(x), a(x), b(x)\) are monic polynomials in \(F[x]\) with \(p(x) = a(x) b(x)\) and with \(p(x) \in R[x]\), \(a(x)\) not in \(R[x]\), and both \(a(x), b(x)\) not constant.
Prove that \(R\) is not a UFD.
(You may assume Gauss’ lemma)
-
Prove that \({\mathbf{Z}}[2\sqrt{2}]\) is not a UFD.
Hint: let \(p(x) = x^2-2\).
- Gauss’ lemma: for \(R\) a UFD with fraction field \(F\), if \(f\) is reducible in \(F[x]\) with \(f=pq\) then there are \(r,s\in R\) such that \(f = (rp)(sq)\) reduces in \(R[x]\).
- Corollary: \(R\) is a UFD iff \(R[x]\) is a UFD.
- The important assumption is \(a(x)\not\in R[x]\), we’ll assume \(R\) is a UFD and try to contradict this.
- Write \(f(x) = a(x)b(x)\in F[x]\), then if \(R\) is a UFD we have \(r,s\in F\) such that \(f(x) = ra(x) sb(x) \in R[x]\).
- Since \(a(x), b(x)\) are monic and \(f=ab\), \(f\) is monic, and by the factorization in \(R[x]\) we have \(rs=1\). So \(r,s\in R^{\times}\).
- Then using that \(ra(x)\in R[x]\), we have \(r^{-1}ra(x) = a(x)\in R[x]\). \(\contradiction\)
- Set \(R = {\mathbf{Z}}[2\sqrt 2], F = {\mathbf{Q}}[2\sqrt 2]\).
- Let \(p(x) \coloneqq x^2-2 \in R[x]\) which splits as \(p(x) = (x+ \sqrt{2} )(x - \sqrt{2} ) \coloneqq a(x) b(x) \in F[x]\).
-
Note neither \(a(x), b(x)\) are in \(R[x]\).
- Explicitly, every monic linear \(p\in R[x]\) is of the form \(x + 2t\sqrt{2}\) with \(t\in {\mathbf{Z}}\), and \(\pm \sqrt{2} \neq 2t\sqrt{2}\) for any \(t\).
- So we have \(p(x) \in R[x]\) splitting as \(p=ab\) in \(F[x]\) with \(a\not \in R[x]\), so part (a) applies.
Ideals (Prime, Maximal, Proper, Principal, etc)
Fall 2021 #5
Let \(R\) be an algebra over \(\mathbb{C}\) which is finite-dimensional as a \({\mathbf{C}}{\hbox{-}}\)vector space. Recall that an ideal \(I\) of \(R\) can be considered as a \({\mathbf{C}}{\hbox{-}}\)subvector space of \(R\). We define the codimension of \(I\) in \(R\) to be \begin{align*} \operatorname{codim}_R I \coloneqq \dim_{{\mathbf{C}}} R - \dim_{{\mathbf{C}}} I ,\end{align*} the difference between the dimension of \(R\) as a \(\mathbb{C}{\hbox{-}}\)vector space, \(\dim_{{\mathbf{C}}} R\), and the dimension of \(I\) as a \({\mathbf{C}}{\hbox{-}}\)vector space, \(\dim_{\mathbf{C}}I\).
-
Show that any maximal ideal \(m \subset R\) has codimension 1 .
-
Suppose that \(\operatorname{dim}_{C} R=2\). Show that there exists a surjective homomorphism of \({\mathbf{C}}{\hbox{-}}\)algebras from the polynomial ring \({\mathbf{C}}[t]\) to \(R\).
- Classify such algebras \(R\) for which \(\dim_{{\mathbf{C}}} R=2\), and list their maximal ideals.
(DZG): my impression is that this is an unusually difficult problem, or was something specifically covered in this year’s qual class.
Fall 2013 #3
-
Define prime ideal, give an example of a nontrivial ideal in the ring \({\mathbf{Z}}\) that is not prime, and prove that it is not prime.
-
Define maximal ideal, give an example of a nontrivial maximal ideal in \({\mathbf{Z}}\) and prove that it is maximal.
-
\({\mathfrak{p}}\) is prime iff \(xy\in {\mathfrak{p}}\implies x\in {\mathfrak{p}}\) or \(y\in {\mathfrak{p}}\).
- An ideal \(I{~\trianglelefteq~}{\mathbf{Z}}\) that is not prime: \(I \coloneqq 8{\mathbf{Z}}\).
- For example, \(2\cdot 4\in 8{\mathbf{Z}}\) but neither 2 nor 4 is a multiple of 8.
-
\({\mathfrak{m}}\) is maximal iff whenever \(I\supseteq{\mathfrak{m}}\) is an ideal in \(R\), then either \(I={\mathfrak{m}}\) or \(I = R\).
- A maximal ideal in \({\mathbf{Z}}\): \(p{\mathbf{Z}}\). This is because primes are maximal in a PID and \(p{\mathbf{Z}}\) is a prime ideal. Alternatively, “to contain is to divide” holds for Dedekind domains, so \(m{\mathbf{Z}}\supseteq p{\mathbf{Z}}\iff m\divides p\), which forces \(m=1,p\), so either \(m{\mathbf{Z}}= p{\mathbf{Z}}\) or \(m{\mathbf{Z}}= {\mathbf{Z}}\).
Fall 2014 #8
Let \(R\) be a nonzero commutative ring without unit such that \(R\) does not contain a proper maximal ideal. Prove that for all \(x\in R\), the ideal \(xR\) is proper.
You may assume the axiom of choice.
Fall 2014 #7
Give a careful proof that \({\mathbf{C}}[x, y]\) is not a PID.
- If \(R[x]\) is a PID, then \(R\) is a field (not explicitly used).
- In \(P \coloneqq R[x_1, \cdots, x_n]\), there are degree functions \(\deg_{x_n}: P\to {\mathbf{Z}}_{\geq 0}\).
- The claim is that \(I \coloneqq\left\langle{x, y}\right\rangle\) is not principal.
- Toward a contradiction, if so, then \(\left\langle{x, y}\right\rangle = \left\langle{f}\right\rangle\).
-
So write \(x = fg\) for some \(g\in {\mathbf{C}}[x, y]\), then
- \(\deg_x(x) = 1\), so \(\deg_x(fg) = 1\) which forces \(\deg_x(f) \leq 1\).
- \(\deg_y(y) = 1\), so \(\deg_y(fg) = 1\) which forces \(\deg_y(f) \leq 1\).
- So \(f(x, y) = ax + by + c\) for some \(a,b,c\in {\mathbf{C}}\).
- \(\deg_x(y) = 0\) and thus \(\deg_x(fg) = 0\), forcing \(a=0\)
- \(\deg_y(x) = 0\) and thus \(\deg_y(fg) = 0\), forcing \(b=0\)
- So \(f(x, y) = c \in {\mathbf{C}}\).
- But \({\mathbf{C}}[x]\) is a field, so \(c\) is a unit in \({\mathbf{C}}\) and thus \({\mathbf{C}}[x, y]\), so \(\left\langle{f}\right\rangle = \left\langle{c}\right\rangle = {\mathbf{C}}[x, y]\).
-
This is a contradiction, since \(1\not\in \left\langle{x, y}\right\rangle\):
- Every element in \(\alpha(x, y) \in\left\langle{x, y}\right\rangle\) is of the form \(\alpha(x, y) = xp(x, y) + yq(x, y)\).
- But \(\deg_x(\alpha) \geq 1, \deg_y(\alpha)\geq 1\), while \(\deg_x(1) = \deg_y(1) = 0\).
- So \(\left\langle{x, y}\right\rangle \neq {\mathbf{C}}[x, y]\).
- Alternatively, \(\left\langle{x, y}\right\rangle\) is proper since \({\mathbf{C}}[x, y] / \left\langle{x, y}\right\rangle \cong {\mathbf{C}}\neq {\mathbf{C}}[x, y]\).
Spring 2019 #6
Let \(R\) be a commutative ring with 1.
Recall that \(x \in R\) is nilpotent iff \(xn = 0\) for some positive integer \(n\).
-
Show that every proper ideal of \(R\) is contained within a maximal ideal.
-
Let \(J(R)\) denote the intersection of all maximal ideals of \(R\). Show that \(x \in J(R) \iff 1 + rx\) is a unit for all \(r \in R\).
- Suppose now that \(R\) is finite. Show that in this case \(J(R)\) consists precisely of the nilpotent elements in R.
-
Definitions: \begin{align*} N(R) &\coloneqq\left\{{x\in R {~\mathrel{\Big\vert}~}x^n = 0 \text{ for some } n}\right\} \\ J(R) &\coloneqq\cap_{{\mathfrak{m}}\in \operatorname{mSpec}} {\mathfrak{m}} .\end{align*}
-
Zorn’s lemma: if \(P\) is a poset in which every chain has an upper bound, \(P\) contains a maximal element.
Define the set of proper ideals \begin{align*} S = \left\{{J {~\mathrel{\Big\vert}~}I \subseteq J < R}\right\} ,\end{align*}
which is a poset under set inclusion.
Given a chain \(J_1 \subseteq \cdots\), there is an upper bound \(J \coloneqq\cup J_i\), so Zorn’s lemma applies.
\(\implies\):
-
We will show that \(x\in J(R) \implies 1+x \in R^{\times}\), from which the result follows by letting \(x=rx\).
-
Let \(x\in J(R)\), so it is in every maximal ideal, and suppose toward a contradiction that \(1+x\) is not a unit.
-
Then consider \(I = \left\langle{1+x}\right\rangle {~\trianglelefteq~}R\). Since \(1+x\) is not a unit, we can’t write \(s(1+x) = 1\) for any \(s\in R\), and so \(1 \not\in I\) and \(I\neq R\)
-
So \(I < R\) is proper and thus contained in some maximal proper ideal \(\mathfrak{m} < R\) by part (1), and so we have \(1+x \in \mathfrak{m}\). Since \(x\in J(R)\), \(x\in \mathfrak{m}\) as well.
-
But then \((1+x) - x = 1 \in \mathfrak{m}\) which forces \(\mathfrak{m} = R\).
\(\impliedby\)
-
Fix \(x\in R\), and suppose \(1+rx\) is a unit for all \(r\in R\).
-
Suppose towards a contradiction that there is a maximal ideal \(\mathfrak{m}\) such that \(x\not \in \mathfrak{m}\) and thus \(x\not\in J(R)\).
-
Consider \begin{align*} M' \coloneqq\left\{{rx + m {~\mathrel{\Big\vert}~}r\in R,~ m\in M}\right\} .\end{align*}
-
Since \(\mathfrak{m}\) was maximal, \(\mathfrak{m} \subsetneq M'\) and so \(M' = R\).
-
So every element in \(R\) can be written as \(rx + m\) for some \(r\in R, m\in M\). But \(1\in R\), so we have \begin{align*} 1 = rx + m .\end{align*}
-
So let \(s = -r\) and write \(1 = sx - m\), and so \(m = 1 + sx\).
-
Since \(s\in R\) by assumption \(1+sx\) is a unit and thus \(m \in \mathfrak{m}\) is a unit, a contradiction.
-
So \(x\in \mathfrak{m}\) for every \(\mathfrak{m}\) and thus \(x\in J(R)\).
\(\mathfrak N(R) \subseteq J(R)\):
- Use the fact \(x\in \mathfrak N(R) \implies x^n = 0 \implies 1 + rx\) is a unit \(\iff x\in J(R)\) by (b): \begin{align*} \sum_{k=1}^{n-1} (-x)^k = \frac{1 - (-x)^n}{1- (-x)} = (1+x)^{-1} .\end{align*}
\(J(R) \subseteq \mathfrak N(R)\):
-
Let \(x \in J(R) \setminus \mathfrak N(R)\).
-
Since \(R\) is finite, \(x^m = x\) for some \(m > 0\).
-
Without loss of generality, we can suppose \(x^2 = x\) by replacing \(x^m\) with \(x^{2m}\).
-
If \(1-x\) is not a unit, then \(\left\langle{1-x}\right\rangle\) is a nontrivial proper ideal, which by (a) is contained in some maximal ideal \({\mathfrak{m}}\). But then \(x\in {\mathfrak{m}}\) and \(1-x \in {\mathfrak{m}}\implies x + (1-x) = 1 \in {\mathfrak{m}}\), a contradiction.
-
So \(1-x\) is a unit, so let \(u = (1-x)^{-1}\).
-
Then \begin{align*} (1-x)x &= x - x^2 = x - x = 0 \\ &\implies u (1-x)x = x = 0 \\ &\implies x=0 .\end{align*}
Spring 2018 #8
Let \(R = C[0, 1]\) be the ring of continuous real-valued functions on the interval \([0, 1]\). Let I be an ideal of \(R\).
-
Show that if \(f \in I, a \in [0, 1]\) are such that \(f (a) \neq 0\), then there exists \(g \in I\) such that \(g(x) \geq 0\) for all \(x \in [0, 1]\), and \(g(x) > 0\) for all \(x\) in some open neighborhood of \(a\).
-
If \(I \neq R\), show that the set \(Z(I) = \{x \in [0, 1] {~\mathrel{\Big\vert}~}f(x) = 0 \text{ for all } f \in I\}\) is nonempty.
- Show that if \(I\) is maximal, then there exists \(x_0 \in [0, 1]\) such that \(I = \{ f \in R {~\mathrel{\Big\vert}~}f (x_0 ) = 0\}\).
Cool problem, but pretty specific topological tricks needed.
- Suppose \(c\coloneqq f(a)\neq 0\), noting that \(c\) may not be positive.
- By continuity, pick \({\varepsilon}\) small enough so that \({\left\lvert {x-a} \right\rvert}<{\varepsilon}\implies {\left\lvert {f(x) - f(a)} \right\rvert} < c/2\). Since we’re on the interval, we have \(f(x) \in (f(a) - c/2, f(a) + c/2) = (c/2, 3c/2)\) which is a ball of radius \(c/2\) about \(c\), which thus doesn’t intersect \(0\).
- So \(f(x) \neq 0\) on this ball, and \(g \coloneqq f^2 > 0\) on it. Note that ideals are closed under products, so \(g\in I\)
- Moreover \(f^2(x) \geq 0\) since squares are non-negative, so \(g\geq 0\) on \([0, 1]\).
- By contrapositive, suppose \(V(I)= \emptyset\), we’ll show \(I\) contains a unit and thus \(I=R\).
- For each fixed \(x\in [0, 1]\), since \(V(I)\) is empty there is some \(f_x\) such that \(f_x(x) \neq 0\).
- By (a), there is some \(g_x\) with \(g_x(x) > 0\) on a neighborhood \(U_x\ni x\) and \(g_x \geq 0\) everywhere.
- Ranging over all \(x\) yields a collection \(\left\{{(g_x, U_x) {~\mathrel{\Big\vert}~}x\in [0, 1]}\right\}\) where \(\left\{{U_x}\right\}\rightrightarrows[0, 1]\).
- By compactness there is a finite subcover, yielding a finite collection \(\left\{{(g_k, U_k)}\right\}_{k=1}^n\) for some \(n\).
- Define the candidate unit as \begin{align*} G(x) \coloneqq{1\over \sum_{k=1}^n g_k(x)} .\end{align*}
- This is well-defined: fix an \(x\), then the denominator is zero at \(x\) iff \(g_k(x) = 0\) for all \(k\). But since the \(U_k\) form an open cover, \(x\in U_\ell\) for some \(\ell\), and \(g_\ell > 0\) on \(U_\ell\).
- Since ideals are closed under sums, \(H\coloneqq{1\over G} \coloneqq\sum g_k \in I\). But \(H\) is clearly a unit since \(HG = \operatorname{id}\).
- If \(I{~\trianglelefteq~}R\) is maximal, \(I\neq R\), and so by (b) we have \(V(I) \neq \emptyset\).
- So there is some \(x_0\in[0, 1]\) with \(f(x_0) = 0\) for all \(f\in I\).
-
Define \({\mathfrak{m}}_{x_0} \coloneqq\left\{{f\in R {~\mathrel{\Big\vert}~}f(x_0) = 0}\right\}\), which is clearly an ideal.
- This is a proper ideal, since constant nonzero functions are continuous and thus in \(R\), not not \({\mathfrak{m}}_{x_0}\).
- We thus have \(I \subseteq {\mathfrak{m}}_{x_0}\), and by maximality they are equal.
\todo[inline]{I'm not super convinced by c!}
Zero Divisors and Nilpotents
Spring 2014 #5
Let \(R\) be a commutative ring and \(a\in R\). Prove that \(a\) is not nilpotent \(\iff\) there exists a commutative ring \(S\) and a ring homomorphism \(\phi: R\to S\) such that \(\phi(a)\) is a unit.
Note: by definition, \(a\) is nilpotent \(\iff\) there is a natural number \(n\) such that \(a^n = 0\).
\(\not A\implies \not B\):
- Suppose \(a\) is nilpotent, so \(a^m = 0_R\), and suppose \(\phi: R\to S\) is a ring morphism.
- Ring morphisms send zero to zero, so \(0_S = \phi(0_R) = \phi(a^m) = \phi(a)^m\) and \(\phi(a)\) is nilpotent.
- But nontrivial rings can’t contain nilpotent units: if \(u\) is a unit and \(ut= 1\) with \(u^k=0\), then \(1 = 1^k = (ut)^k = u^k t^k=0\) and \(R=0\).
\(A\implies B\):
- If \(a\) is not nilpotent, localize at the infinite multiplicative subset \(A \coloneqq\left\{{1, a, a^2, \cdots}\right\}\) to obtain $R \left[ { \scriptstyle { {A}^{-1}} } \right] $. Since \(0\not\in A\), this is not the zero ring.
- By the universal property, there is a map $\phi: R\to R \left[ { \scriptstyle { {A}^{-1}} } \right] $, and the claim is that \(\phi(a)\) is a unit in $R \left[ { \scriptstyle { {A}^{-1}} } \right] $.
- More directly, \(\phi(a) = [a/1] \in \left\{{p,q {~\mathrel{\Big\vert}~}p\in R, q\in A}\right\}\), which has inverse \([a/1]\).
Spring 2021 #5
Suppose that \(f(x) \in ({\mathbf{Z}}/n{\mathbf{Z}})[x]\) is a zero divisor. Show that there is a nonzero \(a\in {\mathbf{Z}}/n{\mathbf{Z}}\) with \(af(x) = 0\).
- Write \(f(x) = \sum_{k=0}^n a_k x^k\), and supposing it’s a zero divisor choose \(g(x) = \sum_{k=0}^m b_k x^k\) of minimal degree so that \(g\neq 0, b_m\neq 0\), and \(f(x)g(x) = 0\).
- The claim is that the top coefficient \(b_m\) will suffice.
- Write the product: \begin{align*} 0 = f(x)g(x) = (a_0 + \cdots + a_{n-1}x^{n-1} + a_n x^n) (b_0 + \cdots + b_{m-1}x^{m-1} + b_m x^m) .\end{align*}
-
Equating coefficients, the coefficient for \(x^{m+n}\) must be zero, so (importantly) \(a_n b_m = 0\).
- Since \(a_n b_m=0\), consider \(a_ng(x)\). This has degree \(d_1 \leq m-1\) but satisfies \(a_ng(x)f(x) = a_n(g(x)f(x)) = 0\), so by minimality \(a_ng(x) = 0\).
- This forces \(a_n b_0 = \cdots = a_n b_{m-1} = 0\), so \(a_n\) annihilates all of the \(b_k\).
-
Now consider the coefficient of \(x^{m+n-1}\), given by \(a_{n-1}b_m + a_{n}b_{m-1}\).
- The second term \(a_n b_{m-1}=0\) since \(a_n\) annihilates all \(b_k\), so (importantly) \(a_{n-1} b_m = 0\).
-
Considering now \(a_{n-1}g(x)\):
- The same argument shows this has degree \(d_2 \leq m-1\) but \(a_{n-1}g(x)f(x) = 0\), so \(a_{n-1}g(x) = 0\).
- So \(a_{n-1}\) annihilates all \(b_k\), and allowing this process to continue inductively.
-
For good measure, the coefficient of \(x^{m+n-2}\) is \(a_{n-2}b_m + a_{n-1}b_{m-1} + a_{n}b_{m-2}\).
- Note that \(a_n, a_{n-1}\) annihilate all \(b_k\), so (importantly) \(a_{n-2} b_m=0\), and so on.
- Thus \(a_k b_m = 0\) for all \(0\leq k \leq n\), and by linearity and commutativity, we have \begin{align*} b_m f(x) = b_m \sum_{k=0}^n a_k x^k = \sum_{k=0}^n (b_m a_k) x^k = 0 .\end{align*}
Fall 2018 #7
Let \(R\) be a commutative ring.
-
Let \(r \in R\). Show that the map \begin{align*} r\bullet : R &\to R \\ x &\mapsto r x .\end{align*} is an \(R{\hbox{-}}\)module endomorphism of \(R\).
-
We say that \(r\) is a zero-divisor if \(r\bullet\) is not injective. Show that if \(r\) is a zero-divisor and \(r \neq 0\), then the kernel and image of \(R\) each consist of zero-divisors.
-
Let \(n \geq 2\) be an integer. Show: if \(R\) has exactly \(n\) zero-divisors, then \({\sharp}R \leq n^2\) .
-
Show that up to isomorphism there are exactly two commutative rings \(R\) with precisely 2 zero-divisors.
You may use without proof the following fact: every ring of order 4 is isomorphic to exactly one of the following: \begin{align*} \frac{ {\mathbf{Z}}}{ 4{\mathbf{Z}}}, \quad \frac{ \frac{ {\mathbf{Z}}}{ 2{\mathbf{Z}}} [t]}{(t^2 + t + 1)}, \quad \frac{ \frac{ {\mathbf{Z}}}{ 2{\mathbf{Z}}} [t]}{ (t^2 - t)}, \quad \frac{ \frac{ {\mathbf{Z}}}{2{\mathbf{Z}}}[t]}{(t^2 )} .\end{align*}
- Testing module morphisms: \(\phi(sm + n) = s\phi(m) + \phi(n)\).
- First isomorphism theorem used for sizes: \(R/\ker f \cong \operatorname{im}f\), so \({\sharp}R = {\sharp}\ker f \cdot {\sharp}\operatorname{im}f\).
- See 1964 Annals “Properties of rings with a finite number of zero divisors”
- Let \(\phi\) denote the map in question, it suffices to show that \(\phi\) is \(R{\hbox{-}}\)linear, i.e. \(\phi(s\mathbf{x} + \mathbf{y}) = s\phi(\mathbf{x}) + \phi(\mathbf{y})\): \begin{align*} \phi(s\mathbf{x} + \mathbf{y}) &= r(s\mathbf{x} + \mathbf{y}) \\ &= rs\mathbf{x} + r\mathbf{y} \\ &= s(r\mathbf{x}) + (r\mathbf{y}) \\ &= s\phi(\mathbf{x}) + \phi(\mathbf{y}) .\end{align*}
Let \(\phi_r(x) \coloneqq rx\) be the multiplication map.
-
Let \(x\in \ker \phi_r \coloneqq\left\{{x\in R {~\mathrel{\Big\vert}~}rx = 0}\right\}\).
-
Since \(R\) is commutative \(0 = rx = xr\), and so \(r\in \ker \phi_x\), so \(\ker \phi_x \neq 0\) and \(x\) is a zero divisor by definition.
-
Let \(y\in \operatorname{im}\phi_r \coloneqq\left\{{y \coloneqq rx {~\mathrel{\Big\vert}~}x\in R}\right\}\), we want to show \(\ker \phi_y\) is nontrivial by producing some \(z\) such that \(yz=0\). Write \(y\coloneqq rx\) for some \(x\in R\).
-
Since \(r\) is a zero divisor, we can produce some \(z\neq 0 \in \ker \phi_r\), so \(rz = 0\).
-
Now using that \(R\) is commutative, we can compute \begin{align*} yz = (rx)z = (xr)z = x (rz) = x(0) = 0 ,\end{align*} so \(z\in \ker \phi_y\).
-
Let \(Z \coloneqq\left\{{z_i}\right\}_{i=1}^n\) be the set of \(n\) zero divisors in \(R\).
-
Let \(\phi_i\) be the \(n\) maps \(x \mapsto z_i x\), and let \(K_i = \ker \phi_i\) be the corresponding kernels.
-
Fix an \(i\).
-
By (b), \(K_i\) consists of zero divisors, so \begin{align*} {\left\lvert {K_i} \right\rvert} \leq n < \infty \quad \text{for each } i .\end{align*}
-
Now consider \(R/K_i \coloneqq\left\{{r + K_i}\right\}\).
-
By the first isomorphism theorem, \(R/K_i \cong \operatorname{im}\phi\), and by (b) every element in the image is a zero divisor, so \begin{align*} [R: K_i] = {\left\lvert {R/K_i} \right\rvert} = {\left\lvert {\operatorname{im}\phi_i} \right\rvert} \leq n .\end{align*}
-
But then \begin{align*} {\left\lvert {R} \right\rvert} = [R:K_i]\cdot {\left\lvert {K_i} \right\rvert} \leq n\cdot n = n^2 .\end{align*}
-
By (c), if there are exactly 2 zero divisors then \({\left\lvert {R} \right\rvert} \leq 4\). Since every element in a finite ring is either a unit or a zero divisor, and \({\left\lvert {R^{\times}} \right\rvert} \geq 2\) since \(\pm 1\) are always units, we must have \({\left\lvert {R} \right\rvert} = 4\).
-
Since the characteristic of a ring must divide its size, we have \(\operatorname{ch}R = 2\) or \(4\).
-
Using the hint, we see that only \({\mathbf{Z}}/(4)\) has characteristic 4, which has exactly 2 zero divisors given by \([0]_4\) and \([2]_4\).
-
If \(R\) has characteristic 2, we can check the other 3 possibilities.
-
We can write \({\mathbf{Z}}/(2)[t]/(t^2) = \left\{{a + bt {~\mathrel{\Big\vert}~}a,b\in {\mathbf{Z}}/(2)}\right\}\), and checking the multiplication table we have \begin{align*} \begin{array}{c|cccc} & 0 & 1 & t & 1+t \\ \hline 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & t & 1+t \\ t & 0 & t & \mathbf{0} & t \\ 1 + t & 0 & 1+t & t & 1 \\ \end{array} ,\end{align*}
and so we find that \(t, 0\) are the zero divisors.
-
In \({\mathbf{Z}}/(2)[t]/(t^2 - t)\), we can check that \(t^2 = t \implies t t^2 = t^2 \implies t(t^2 + 1) = 0 \implies t(t+1) = 0\), so both \(t\) and \(t+1\) are zero divisors, along with zero, so this is not a possibility.
-
Similarly, in \({\mathbf{Z}}/(2)[t]/(t^2 + t + 1)\), we can check the bottom-right corner of the multiplication table to find \begin{align*} \left[\begin{array}{c|cc} & t & 1 +t \\ \hline t & 1+t & 1 \\ t & 1 & t \\ \end{array}\right] ,\end{align*}
and so this ring only has one zero divisor.
-
Thus the only possibilities are: \begin{align*} R &\cong {\mathbf{Z}}/(4) \\ R &\cong {\mathbf{Z}}/(2)[t] / (t^2) .\end{align*}
Zorn’s Lemma
Fall 2013 #4
Let \(R\) be a commutative ring with \(1\neq 0\). Recall that \(x\in R\) is nilpotent iff \(x^n = 0\) for some positive integer \(n\).
-
Show that the collection of nilpotent elements in \(R\) forms an ideal.
-
Show that if \(x\) is nilpotent, then \(x\) is contained in every prime ideal of \(R\).
-
Suppose \(x\in R\) is not nilpotent and let \(S = \left\{{x^n {~\mathrel{\Big\vert}~}n\in {\mathbb{N}}}\right\}\). There is at least on ideal of \(R\) disjoint from \(S\), namely \((0)\).
By Zorn’s lemma the set of ideals disjoint from \(S\) has a maximal element with respect to inclusion, say \(I\). In other words, \(I\) is disjoint from \(S\) and if \(J\) is any ideal disjoint from \(S\) with \(I\subseteq J \subseteq R\) then \(J=I\) or \(J=R\).
Show that \(I\) is a prime ideal.
-
Deduce from (a) and (b) that the set of nilpotent elements of \(R\) is the intersection of all prime ideals of \(R\).
Fall 2015 #3
Let \(R\) be a rng (a ring without 1) which contains an element \(u\) such that for all \(y\in R\), there exists an \(x\in R\) such that \(xu=y\).
Prove that \(R\) contains a maximal left ideal.
Hint: imitate the proof (using Zorn’s lemma) in the case where \(R\) does have a 1.
-
Define the map \begin{align*} \phi_u: R &\to R\\ x &\mapsto xu ,\end{align*} which is right-multiplication by \(u\). By assumption, \(\phi_u\) is surjective, so the principal ideal \(Ru\) equals \(R\).
-
Then \(K \coloneqq\ker \phi_u \in \operatorname{Id}(R)\) is an ideal.
-
\(K\) is proper – otherwise, noting \(Ru=R\), if \(K=R\) we have \(Ru = 0\) and thus \(R=0\). So suppose \(R\neq 0\).
-
Take a poset \(S \coloneqq\left\{{J\in \operatorname{Id}(R) {~\mathrel{\Big\vert}~}J \supseteq K, J\neq R}\right\}\), the set of all ideals containing \(K\), ordered by subset inclusion. Note that \(K \in S\), so \(S\) is nonempty.
-
Apply Zorn’s lemma: let \(C: C_1 \subseteq C_2 \subseteq \cdots\) be a chain (totally ordered sub-poset) in \(S\). If \(C\) is the empty chain, \(K\) is an upper bound. Otherwise, if \(C\) is nonempty, define \(\widehat{C} \coloneqq\bigcup_{i=1}^\infty C_i\).
- \(\widehat{C}\) is an ideal: if \(a,b\in \widehat{C}\), then \(a\in C_i, b\in C_j\) for some \(i,j\). But without loss of generality, using that chains are totally ordered, \(C_i \subseteq C_j\), so \(a,b\in C_j\) and thus \(ab\in C_j\). Similarly for \(x\in \widehat{C}\), \(x\in C_j\) for some \(j\), and thus \(Rx \subseteq C_j\) since \(C_j\) is an ideal.
-
\(\widehat{C}\) is in \(S\): It clearly contains \(K\), since for example \(K \subseteq C_1 \subseteq \widehat{C}\).
- That \(\widehat{C} \neq R\): an ideal equals \(R\) iff it contains a unit. But if \(r\in \widehat{C}\) is a unit, \(r\in C_j\) for some \(j\) is a unit, making \(C_j=R\). \(\contradiction\)
-
So by Zorn’s lemma, \(\widehat{C}\) contains a maximal ideal (incidentally containing \(K\)).
Spring 2015 #7
Let \(R\) be a commutative ring, and \(S\subset R\) be a nonempty subset that does not contain 0 such that for all \(x, y\in S\) we have \(xy\in S\). Let \({\mathcal{I}}\) be the set of all ideals \(I{~\trianglelefteq~}R\) such that \(I\cap S = \emptyset\).
Show that for every ideal \(I\in {\mathcal{I}}\), there is an ideal \(J\in {\mathcal{I}}\) such that \(I\subset J\) and \(J\) is not properly contained in any other ideal in \({\mathcal{I}}\).
Prove that every such ideal \(J\) is prime.
- Restating, take the poset \(S\coloneqq\left\{{J\in \operatorname{Id}(R) {~\mathrel{\Big\vert}~}J \cap S = \emptyset, I\neq R, I \subseteq J}\right\}\) ordered by inclusion. Note that \(S\) is nonempty since it contains \(I\). It suffices to produce a maximal element of \(S\).
- Applying Zorn’s lemma, let \(C: C_1 \subseteq C_2 \subseteq \cdots\) be a chain and define \(\widehat{C} \coloneqq\cup C_i\).
- By standard arguments, \(\widehat{C} \in \operatorname{Id}(R)\) and \(\widehat{C} \supseteq I\), and it suffices to show \(\widehat{C} \cap S = \emptyset\) and \(\widehat{C}\neq R\).
-
\(\widehat{C} \cap S = \emptyset\):
- By contradiction, if \(x\in \widehat{C} \cap S\) then \(x\in C_j\) for some \(j\), and \(x\in S\). But then \(x \in C_j \cap S = \emptyset\).
-
\(\widehat{C} \neq R\):
- By contradiction, if so then \(1 \in \widehat{C} \implies 1 \in C_j\) for some \(j\), forcing \(C_j = R\).
- So Zorn’s lemma applies and we obtain some ideal \({\mathfrak{p}}\), which we now claim is prime.
- Let \(ab\in {\mathfrak{p}}\), we want to show \(a\in {\mathfrak{p}}\) or \(b\in{\mathfrak{p}}\).
- Suppose not, then neither \(a,b\in {\mathfrak{p}}\). By maximality, \({\mathfrak{p}}+ Ra = R\), and so \({\mathfrak{p}}+ Ra\) intersects \(S\). Similarly \({\mathfrak{p}}+ Rb = R\) so \({\mathfrak{p}}+ Rb\) intersects \(S\).
- Produce elements \(x\coloneqq p_1 + r_1a, y\coloneqq p_2 + r_2b\in S\), then since \(S\) is multiplicatively closed, \begin{align*} xy&\coloneqq(p_1 + r_1 a)(p_2 + r_2b)\in S \\ &\implies p_1 p_2 + p_1r_2 b + p_2 r_1 a + r_1 r_2 ab \in S \\ &\implies xy\in {\mathfrak{p}}+ {\mathfrak{p}}Rb + {\mathfrak{p}}Ra + R{\mathfrak{p}}&& \text{since } p_i, ab\in {\mathfrak{p}}\\ &\implies xy \in ({\mathfrak{p}}+ Rb + Ra + R){\mathfrak{p}}\subseteq {\mathfrak{p}} .\end{align*} But then \(xy\in S \cap{\mathfrak{p}}\), a contradiction.
Spring 2013 #1
Let \(R\) be a commutative ring.
-
Define a maximal ideal and prove that \(R\) has a maximal ideal.
-
Show than an element \(r\in R\) is not invertible \(\iff r\) is contained in a maximal ideal.
-
Let \(M\) be an \(R{\hbox{-}}\)module, and recall that for \(0\neq \mu \in M\), the annihilator of \(\mu\) is the set \begin{align*} \operatorname{Ann}(\mu) = \left\{{r\in R {~\mathrel{\Big\vert}~}r\mu = 0}\right\} .\end{align*} Suppose that \(I\) is an ideal in \(R\) which is maximal with respect to the property that there exists an element \(\mu \in M\) such that \(I = \operatorname{Ann}(\mu)\) for some \(\mu \in M\). In other words, \(I = \operatorname{Ann}(\mu)\) but there does not exist \(\nu\in M\) with \(J = \operatorname{Ann}(\nu) \subsetneq R\) such that \(I\subsetneq J\).
Prove that \(I\) is a prime ideal.
- Maximal: a proper ideal \(I{~\trianglelefteq~}R\), so \(I\neq R\), such that if \(J\supseteq I\) is any other ideal, \(J = R\).
- Existence of a maximal ideal: use that \(0\in \operatorname{Id}(R)\) always, so \(S\coloneqq\left\{{I\in \operatorname{Id}(R) {~\mathrel{\Big\vert}~}I\neq R}\right\}\) is a nonempty poset under subset inclusion. Applying the usual Zorn’s lemma argument produces a maximal element.
\(\impliedby\): By contrapositive: if \(r\in R\) is a unit and \({\mathfrak{m}}\) is maximal, then \(r\in {\mathfrak{m}}\implies {\mathfrak{m}}= R\), contradicting that \({\mathfrak{m}}\) is proper.
\(\implies\):
- Suppose \(a\) is not a unit, we’ll produce a maximal ideal containing it.
- Let \(I\coloneqq Ra\) be the principal ideal generated by \(a\), then \(Ra \neq R\) since \(a\) is not a unit.
-
Take a poset \(S \coloneqq\left\{{J\in \operatorname{Id}(R) {~\mathrel{\Big\vert}~}J\supseteq Ra, J\neq R}\right\}\) ordered by set inclusion.
-
Let \(C_*\) be a chain in \(S\), set \(\widehat{C} \coloneqq\cup C_i\). Then \(\widehat{C} \in S\):
- \(\widehat{C} \neq R\), since if so it contains a unit, forcing some \(C_i\) to contain a unit and thus equal \(R\).
- \(\widehat{C} \supseteq Ra\), since e.g. \(\widehat{C} \supseteq C_1 \supseteq Ra\).
- \(\widehat{C}\) is an ideal since \(xy\in \widehat{C} \implies x\in C_i, y\in C_j\) and \(C_i \subseteq C_j\) without loss of generality, so \(xy\in C_j \subseteq \widehat{C}\).
-
- Then \(Ra \subseteq \widehat{C}\), some maximal ideal.
- Write \(I \coloneqq\operatorname{Ann}(u)\) for some \(u\), and toward a contradiction suppose \(ab\in I\) but \(a,b\not\in I\).
- Then \(abu=0\) but \(au\neq 0, bu\neq 0\).
- Since \(abu=0\), we have \(a\in \operatorname{Ann}(bu)\). Note that \(\operatorname{Ann}(bu) \supseteq\operatorname{Ann}(u)\), since \(su = 0\implies bsu=sbu=0\).
- We can’t have \(\operatorname{Ann}(bu) = R\), since if \(sbu=0\) for all \(s\in R\), so we could take \(s=1\) to get \(bu=0\) and \(b\in \operatorname{Ann}(u)\).
- By maximality, this forces \(\operatorname{Ann}(u) = \operatorname{Ann}(bu)\), so \(sbu = 0 \implies su=0\) for any \(s\in R\).
- Now take \(s=a\), and since \(abu=0\) we get \(au=0\) and \(a\in \operatorname{Ann}(u)\). \(\contradiction\)
Fall 2019 #6
Let \(R\) be a commutative ring with multiplicative identity. Assume Zorn’s Lemma.
-
Show that \begin{align*} N = \{r \in R \mathrel{\Big|}r^n = 0 \text{ for some } n > 0\} \end{align*} is an ideal which is contained in any prime ideal.
-
Let \(r\) be an element of \(R\) not in \(N\). Let \(S\) be the collection of all proper ideals of \(R\) not containing any positive power of \(r\). Use Zorn’s Lemma to prove that there is a prime ideal in \(S\).
- Suppose that \(R\) has exactly one prime ideal \(P\) . Prove that every element \(r\) of \(R\) is either nilpotent or a unit.
-
Prime ideal: \(\mathfrak{p}\) is prime iff \(ab \in \mathfrak{p} \implies a\in \mathfrak{p}\) or \(b\in \mathfrak{p}\).
-
Silly fact: 0 is in every ideal!
-
Zorn’s Lemma: Given a poset, if every chain has an upper bound, then there is a maximal element. (Chain: totally ordered subset.)
-
Corollary: If \(S\subset R\) is multiplicatively closed with \(0\not\in S\) then \(\left\{{I {~\trianglelefteq~}R {~\mathrel{\Big\vert}~}J\cap S = \emptyset}\right\}\) has a maximal element.
\todo[inline]{Prove this} -
Theorem: If \(R\) is commutative, maximal \(\implies\) prime for ideals.
\todo[inline]{Prove this} -
Theorem: Non-units are contained in a maximal ideal. (See HW?)
- Let \(\mathfrak{p}\) be prime and \(x\in N\).
- Then \(x^k = 0 \in \mathfrak{p}\) for some \(k\), and thus \(x^k = x x^{k-1} \in \mathfrak p\).
- Since \(\mathfrak p\) is prime, inductively we obtain \(x\in\mathfrak p\).
-
Let \(S = \left\{{r^k \mathrel{\Big|}k\in {\mathbb{N}}}\right\}\) be the set of positive powers of \(r\).
-
Then \(S^2 \subseteq S\), since \(r^{k_1}r^{k_2} = r^{k_1+k_2}\) is also a positive power of \(r\), and \(0\not\in S\) since \(r\neq 0\) and \(r\not\in N\).
-
By the corollary, \(\left\{{I {~\trianglelefteq~}R {~\mathrel{\Big\vert}~}I\cap S = \emptyset}\right\}\) has a maximal element \(\mathfrak{p}\).
-
Since \(R\) is commutative, \(\mathfrak{p}\) is prime.
-
Suppose \(R\) has a unique prime ideal \(\mathfrak{p}\).
-
Suppose \(r\in R\) is not a unit, and toward a contradiction, suppose that \(r\) is also not nilpotent.
-
Since \(r\) is not a unit, \(r\) is contained in some maximal (and thus prime) ideal, and thus \(r \in \mathfrak{p}\).
-
Since \(r\not\in N\), by (b) there is a maximal ideal \(\mathfrak{m}\) that avoids all positive powers of \(r\). Since \(\mathfrak{m}\) is prime, we must have \(\mathfrak{m} = \mathfrak{p}\). But then \(r\not\in \mathfrak{p}\), a contradiction.
Noetherian Rings
Fall 2015 #4
Let \(R\) be a PID and \((a_1) < (a_2) < \cdots\) be an ascending chain of ideals in \(R\). Prove that for some \(n\), we have \((a_j) = (a_n)\) for all \(j\geq n\).
- Let \(I\coloneqq\cup Ra_i\) which is an ideal in a PID and thus \(I = Rb\) for some \(b\).
- Using that \(b\in I\), which is a union, we have \(Rb\in Ra_m\) for some \(m\).
- Thus \(I = R_b \subseteq Ra_m\), and \(Ra_m \subseteq I\) by definition of \(I\), so \(Rb = Ra_m\).
- In particular, since \(Ra_{m} \subseteq Ra_{m+1}\) by assumption, and \(Ra_{m+1} \subseteq Rb \subseteq Ra_m\) since \(Rb = I\), we have \(Ra_m = Ra_{m+1}\). So inductively, the chain stabilizes at \(m\).
Spring 2021 #6
-
Carefully state the definition of Noetherian for a commutative ring \(R\).
-
Let \(R\) be a subset of \({\mathbf{Z}}[x]\) consisting of all polynomials \begin{align*} f(x) = a_ 0 + a_1 x + a_2 x^2 + \cdots + a_nx^n \end{align*} such that \(a_k\) is even for \(1\leq k \leq n\). Show that \(R\) is a subring of \({\mathbf{Z}}[x]\).
- Show that \(R\) is not Noetherian.
Hint: consider the ideal generated by \(\left\{{ 2x^k {~\mathrel{\Big\vert}~}1\leq k \in {\mathbf{Z}}}\right\}\).
-
A ring is Noetherian iff \(R\) satisfies the ascending chain condition: every chain of ideals \(A_1 \subseteq A_2 \subseteq \cdots\) eventually stabilizes, so \(A_m \subseteq A_{m+1} = A_{m+2} = \cdots\).
-
That \(R\) is a subring of \({\mathbf{Z}}[x]\):
- \((R, +)\) is an abelian subgroup: note that \(f(x) + g(x) = \sum a_k x^k + \sum b_k x^k = \sum (a_k + b_k) x^k\), so if \(a_k, b_k\) are even then \(a_k + b_k\) is even. It’s closed under inverses, since \(a_k\) is even iff \(-a_k\) is even, and contains zero.
- \((R, \cdot)\) is a submonoid: \(f(x) g(x) = \sum_{n=1}^N \qty{ \sum_{k=1}^n a_k b_{n-k}} x^k\) where without loss of generality, \(\deg f = \deg g = n\) by setting coefficients to zero. Then sums and products of even integers are even, so \(fg \in R\).
-
That \(R\) is not Noetherian: it suffices to show that \(R\) contains an ideal that is not finitely generated.
-
The claim is that setting \(S \coloneqq\left\{{2x^k}\right\}_{k\in {\mathbf{Z}}_{\geq 1}}\) and taking \begin{align*} I \coloneqq\left\langle{S}\right\rangle = \sum_{k\in {\mathbf{Z}}_{\geq 1}} R\cdot 2x^k \coloneqq\left\{{ \sum_{i=1}^m r_k(x) 2x^k {~\mathrel{\Big\vert}~}r_k(x) \in 2{\mathbf{Z}}[x], m\in {\mathbf{Z}}_{\geq 0}}\right\} \end{align*} yields an ideal that is not finitely generated.
-
Suppose toward a contradiction that \(\left\{{g_1, g_2, \cdots, g_M}\right\}\) were a finite generating set, where each \(g_i \in I\).
\todo[inline]{???}
Simple Rings
Fall 2017 #5
A ring \(R\) is called simple if its only two-sided ideals are \(0\) and \(R\).
-
Suppose \(R\) is a commutative ring with 1. Prove \(R\) is simple if and only if \(R\) is a field.
-
Let \(k\) be a field. Show the ring \(M_n (k)\), \(n \times n\) matrices with entries in \(k\), is a simple ring.
- Nonzero proper ideals contain at least one nonzero element.
- \(I=R\) when \(1\in I\).
-
Effects of special matrices: let \(A_{ij}\) be a matrix with only a 1 in the \(ij\) position.
- Left-multiplying \(A_{ij}M\) moves row \(j\) to row \(i\) and zeros out the rest of \(M\).
- Right-multiplying \(MA_{ij}\) moves column \(i\) to column \(j\) and zeros out the rest.
- So \(A_{ij} M A_{kl}\) moves entry \(j, k\) to \(i, l\) and zeros out the rest.
\(\implies\):
- Suppose \(\operatorname{Id}(R) = \left\{{\left\langle{0}\right\rangle, \left\langle{1}\right\rangle}\right\}\). Then for any nonzero \(r\in R\), the ideal \(\left\langle{r}\right\rangle = \left\langle{1}\right\rangle\) is the entire ring.
- In particular, \(1\in \left\langle{r}\right\rangle\), so we can write \(a = tr\) for some \(t\in R\).
- But then \(r\in R^{\times}\) with \(t\coloneqq r^{-1}\).
\(\impliedby\):
- Suppose \(R\) is a field and \(I\in \operatorname{Id}(R)\) is an ideal.
- If \(I \neq \left\langle{0}\right\rangle\) is proper and nontrivial, then \(I\) contains at least one nonzero element \(a\in I\).
- Since \(R\) is a field, \(a^{-1}\in R\), and \(aa^{-1}= 1\in I\) forces \(I = \left\langle{1}\right\rangle\).
- Let \(J{~\trianglelefteq~}R\) be a nonzero two-sided ideal, noting that \(R\) is noncommutative – the claim is that \(J\) contains \(I_n\), the \(n\times n\) identity matrix, and thus \(J = R\).
- Pick a nonzero element \(M\in I\), then \(M\) has a nonzero entry \(m{ij}\).
-
Let \(A_{ij}\) be the matrix with a 1 in the \(i,j\) position and zeros elsewhere.
- Left-multiplying \(A_{ij}M\) moves row \(j\) to row \(i\) and zeros out the rest of \(M\).
- Right-multiplying \(MA_{ij}\) moves column \(i\) to column \(j\) and zeros out the rest.
- So \(A_{ij} M A_{kl}\) moves entry \(j, k\) to \(i, l\) and zeros out the rest.
- So define \(B \coloneqq A_{i, i}MA_{j, i}\), which movies \(m_{ij}\) to the \(i,i\) position on the diagonal and has zeros elsewhere.
- Then \(m_{ij}^{-1}{\varepsilon}_{ii} \coloneqq A_{ii}\) is a matrix with \(1\) in the \(i, i\) spot for any \(i\). Since \(I\) is an ideal, we have \({\varepsilon}_{ii}\in I\) for every \(i\).
- We can write the identity \(I_n\) as \(\sum_{i=1}^n {\varepsilon}_{ii}\), so \(I_n \in I\) and \(I=R\).
Spring 2016 #8
Let \(R\) be a simple rng (a nonzero ring which is not assume to have a 1, whose only two-sided ideals are \((0)\) and \(R\)) satisfying the following two conditions:
- \(R\) has no zero divisors, and
- If \(x\in R\) with \(x\neq 0\) then \(2x\neq 0\), where \(2x\coloneqq x+x\).
Prove the following:
-
For each \(x\in R\) there is one and only one element \(y\in R\) such that \(x = 2y\).
-
Suppose \(x,y\in R\) such that \(x\neq 0\) and \(2(xy) = x\), then \(yz = zy\) for all \(z\in R\).
You can get partial credit for (b) by showing it in the case \(R\) has a 1.
A general opinion is that this is not a great qual problem! Possibly worth skipping.
- \(R\) has no left zero divisors iff \(R\) has the left cancellation property: \(xa=xb \implies a=b\).
- \(R\) has no right zero divisors iff \(R\) has the right cancellation property: \(ax=bx \implies a=b\).
Note: solutions borrowed from folks on Math twitter!
-
Existence: the claim is that \(2R \coloneqq\left\{{2y {~\mathrel{\Big\vert}~}y\in R}\right\}\) is a nontrivial two-sided ideal of \(R\), forcing \(2R = R\) by simpleness.
- That \(2R \neq 0\) follows from condition (1): Provided \(y\neq 0\), we have \(2y\neq 0\), and so if \(R\neq 0\) then there exists some nonzero \(a\in R\), in which case \(2a\neq 0\) and \(2a\in 2R\).
- That \(2R\) is a right ideal: clear, since \((2y)\cdot r = 2(yr)\in 2R\).
- That \(2R\) is a left ideal: use that multiplication is distributive: \begin{align*} r\cdot 2y \coloneqq r(y+y) = ry + ry \coloneqq 2(ry) \in 2R .\end{align*}
- So \(2R = R\) by simpleness.
-
Uniqueness:
- Use the contrapositive of condition (1), so that \(2x = 0 \implies x=0\).
- Suppose toward a contradiction that \(x=2y_1 = 2y_2\), then \begin{align*} 0 = x-x = 2y_1 - 2y_2 = 2(y_1 - y_2) \implies y_1 - y_2 = 0 \implies y_1 = y_2 .\end{align*}
-
First we’ll show \(z=2(yz)\): \begin{align*} xy + xy &= x \\ \implies xy + xy - x &= 0 \\ \implies xyz + xyz - xz &= 0 \\ \implies x(yz + yz - z) &= 0 \\ \implies yz + yz - z &= 0 && \text{since } x\neq 0 \text{ and no zero divisors }\\ \implies 2(yz) &= z .\end{align*}
-
Now we’ll show \(z=2(zy)\): \begin{align*} yz + yz &= z \\ \implies zyz + zyz &= zz \\ \implies zyz + zyz - zz &= 0 \\ \implies (zy + zy - z)z &= 0\\ \implies z=0 \text{ or } zy+zy-z &= 0 && \text{ no zero divisors } .\end{align*}
-
Then if \(z=0\), we have \(yz = 0 = zy\) and we’re done.
-
Otherwise, \(2(zy) = z\), and thus \begin{align*} 2(zy) = z = 2(yz) \implies 2(zy - yz) = 0 \implies zy-yz = 0 ,\end{align*} so \(zy=yz\).
- If \(1\in R\), \begin{align*} 2xy &= x \\ \implies 2xy-x &= 0 \\ \implies x(2y-1) &= 0 \\ \implies 2y-1 &= 0 && x\neq 0 \text{ and no zero divisors}\\ \implies 2y &= 1 .\end{align*}
- Now use \begin{align*} 1\cdot z &= z\cdot 1 \\ \implies (2y)z &= z(2y) \\ \implies (y+y)z &= z(y+y) \\ \implies yz+yz &= zy+zy \\ \implies 2(yz) &= 2(zy) \\ \implies 2(yz-zy) &= 0 \\ \implies yz-zy &= 0 \\ ,\end{align*} using condition (2).
Unsorted
Fall 2019 #3
Let \(R\) be a ring with the property that for every \(a \in R, a^2 = a\).
-
Prove that \(R\) has characteristic 2.
-
Prove that \(R\) is commutative.
- Just fiddle with direct computations.
- Context hint: that we should be considering things like \(x^2\) and \(a+b\).
\begin{align*} 2a = (2a)^2 = 4a^2 = 4a \implies 2a = 0 .\end{align*} Note that this implies \(x = -x\) for all \(x\in R\).
\begin{align*} a+b = (a+b)^2 &= a^2 + ab + ba + b^2 = a + ab + ba + b \\ &\implies ab + ba = 0 \\ &\implies ab = -ba \\ &\implies ab = ba \quad\text{by (a)} .\end{align*}
Spring 2018 #5
Let \begin{align*} M=\left(\begin{array}{ll}{a} & {b} \\ {c} & {d}\end{array}\right) \quad \text{and} \quad N=\left(\begin{array}{cc}{x} & {u} \\ {-y} & {-v}\end{array}\right) \end{align*}
over a commutative ring \(R\), where \(b\) and \(x\) are units of \(R\). Prove that \begin{align*} M N=\left(\begin{array}{ll}{0} & {0} \\ {0} & {*}\end{array}\right) \implies MN = 0 .\end{align*}
-
Multiply everything out to get \begin{align*} { \begin{bmatrix} {ax-by} & {au-bv} \\ {cx-dy} & {cu-dv} \end{bmatrix} } ,\end{align*} so it suffices to show \(cu=dv\) given \begin{align*} ax &= by \\ cx &= dy \\ au &= bv .\end{align*}
-
Writing \(cu\):
- Use that \(b\in R^{\times}\), left-multiply (1) by \(b^{-1}\) to get \(b^{-1}a x = y\)
- Substitute \(y\) into (2) to get \(cx = d(b^{-1}a x)\).
- Since \(x\in R^{\times}\), right-multiply by \(x^{-1}\) to get \(c = db^{-1}a\) and thus \(cu = db^{-1}a u\).
- Summary: \begin{align*} ax = by &\implies b^{-1}ax = y \\ &\implies cx = dy = d(b^{-1}a x) \\ &\implies c = db^{-1}a \\ &\implies cu = db^{-1}au .\end{align*}
-
Writing \(dv\):
- Left-multiply (3) by \(b^{-1}\) to get \(b^{-1}au = v\).
- Left-multiply by \(d\) to get \(db^{-1}au = dv\)
- Summary: \begin{align*} au = bv &\implies b^{-1}a u = v \\ &\implies db^{-1}au = dv .\end{align*}
-
So \begin{align*} cu = db^{-1}a u = dv .\end{align*}
Spring 2014 #6
\(R\) be a commutative ring with identity and let \(n\) be a positive integer.
-
Prove that every surjective \(R{\hbox{-}}\)linear endomorphism \(T: R^n \to R^n\) is injective.
-
Show that an injective \(R{\hbox{-}}\)linear endomorphism of \(R^n\) need not be surjective.
Galois Theory
General Galois Extensions
Fall 2021 #4
Recall that for a given positive integer \(n\), the cyclotomic field \(\mathbb{Q}\left(\zeta_{n}\right)\) is generated by a primitive \(n\)-th root of unity \(\zeta_{n}\).
-
What is the degree of \(Q\left(\zeta_{n}\right)\) over \(Q\) ?
-
Define what it means for a finite field extension \(L / K\) to be Galois, and prove that the cyclotomic field \(Q\left(\zeta_{n}\right)\) is Galois over \(\mathbb{Q}\).
-
What is the Galois group of \(\mathbb{Q}\left(\zeta_{n}\right)\) over \(\mathbb{Q}\) ?
-
How many subfields of \(\mathbb{Q}\left(\zeta_{2021}\right)\) have degree 2 over Q? Note that \(2021=43 \cdot 47\)
Fall 2020 #4
Let \(K\) be a Galois extension of \(F\), and let \(F \subset E \subset K\) be inclusions of fields. Let \(G \coloneqq{ \mathsf{Gal}}(K/F)\) and \(H \coloneqq{ \mathsf{Gal}}(K/E)\), and suppose \(H\) contains \(N_G(P)\), where \(P\) is a Sylow \(p\)-subgroup of \(G\) for \(p\) a prime. Prove that \([E: F] \equiv 1 \operatorname{mod}p\).
The correspondence:
Normalizers: \begin{align*} N_G(P) = \left\{{g\in G {~\mathrel{\Big\vert}~}gPg^{-1}= P}\right\} .\end{align*}
-
Reduce to a group theory problem: \([E:F] = [G:H]\), despite the fact that \(E/F\) is not necessarily Galois. This is because we can count in towers: \begin{align*} [K:F] = [K:E][E:F] &\implies [G:1] = [K:E][H:1] \\ &\implies {\sharp}G = [K:E] {\sharp}H \\ &\implies [G:H] = {{\sharp}G \over {\sharp}H} = [K:E] .\end{align*}
-
Essential fact: if \(P \in {\operatorname{Syl}}_p(G)\), we can use that \(P \subseteq N_G(P) \subset H\) and so \(P\in {\operatorname{Syl}}_p(H)\) as well.
-
Now use that \(N_G(P) \subseteq H\), and do Sylow theory for \(P\) in both \(G\) and \(H\):
- Sylow 3 on \(G\) yields \(n_p(G) = [G: N_G(P)] \equiv 1 \operatorname{mod}p\).
- Sylow 3 on \(H\) yields \(n_p(H) = [G: N_H(P)] \equiv 1 \operatorname{mod}p\).
-
Claim: \(N_H(P) = N_G(P)\).
- We have \(N_H(P) \subseteq N_G(P)\) since \(H \subseteq G\), so \(hPh^{-1}= P\) remains true regarding either \(h\in H\) or \(h\in G\).
- For \(N_G(P) \subseteq N_H(P)\), use that \(N_G(P) \subseteq H\) and so \(gPg^{-1}= P\) implies \(g\in H\), so \(g\in N_H(P)\).
-
Now morally one might want to apply an isomorphism theorem: \begin{align*} {G/ N_G(P) \over H/N_H(P)}= {G/ N_H(P) \over H/N_H(P)}\cong {G\over H} ,\end{align*} but we don’t have normality. However, we can still get away with the corresponding counting argument if everything is finite: \begin{align*} {[G: N_G(P)] \over [H:N_H(P)] }= {[G: N_H(P)] \over [H:N_H(P)] }= {{\sharp}G / {\sharp}N_H(P) \over {\sharp}H / {\sharp}N_H(P)} = {{\sharp}G \over {\sharp}H} = [G: H] .\end{align*}
-
We have an equation of the form \(n_p(G)/n_p(H) = m\), and we want to show \(m\equiv 1 \operatorname{mod}p\). So write \begin{align*} {n_p(G) \over n_p(H) } = m \implies m n_p(H) &= n_p(G) \\ \implies m n_p(H) &\equiv n_p(G) \operatorname{mod}p \\ \implies m\cdot 1 &\equiv 1 \operatorname{mod}p \\ \implies m &\equiv 1 \operatorname{mod}p .\end{align*}
Fall 2019 Midterm #9
Let \(n\geq 3\) and \(\zeta_n\) be a primitive \(n\)th root of unity. Show that \([{\mathbf{Q}}(\zeta_n + \zeta_n^{-1}): {\mathbf{Q}}] = \phi(n)/2\) for \(\phi\) the totient function.
-
Some notation: let \(\alpha_k \coloneqq\zeta_n^k + \zeta_n^{-k}\).
-
Let \(m(x)\) be the minimal polynomial of \(\alpha_1 \coloneqq\zeta_n + \zeta_n^{-1}\). Note that \(\alpha_1 \in {\mathbf{Q}}(\zeta_n)\).
-
Use that \({ \mathsf{Gal}}({\mathbf{Q}}(\zeta_n)/{\mathbf{Q}}) \cong C_n^{\times}\), consisting of maps \(\sigma_k: \zeta \mapsto \zeta^k\) for \(\gcd(k, n) = 1\), of which there are \(\phi(n)\) many.
-
Galois transitively permutes the roots of irreducible polynomials, so the roots of \(m\) are precisely the Galois conjugates of \(\alpha\), i.e. the Galois orbit of \(\alpha\), so we can just compute it. For illustrative purposes, suppose \(n\) is prime, then \begin{align*} \sigma_1(\zeta_n + \zeta_n^{-1}) &= \zeta_n + \zeta_n^{-1}=\alpha_1 \\ \sigma_2(\zeta_n + \zeta_n^{-1}) &= \zeta_n^2 + \zeta_n^{-2} = \alpha_2 \\ \sigma_3(\zeta_n + \zeta_n^{-1}) &= \zeta_n^3 + \zeta_n^{-3} = \alpha_3 \\ \vdots&\\ \sigma_{n-1}(\zeta_n + \zeta_n^{-1}) &= \zeta_n^{n-1} + \zeta_n^{-(n-1)} = \zeta_n^{-1} + \zeta_n^{1} = \alpha_1 \\ \sigma_{n-2}(\zeta_n + \zeta_n^{-1}) &= \zeta_n^{n-2} + \zeta_n^{-(n-2)} = \zeta_n^{-2} + \zeta_n^{2} = \alpha_2 \\ \sigma_{n-3}(\zeta_n + \zeta_n^{-1}) &= \zeta_n^{n-3} + \zeta_n^{-(n-3)} = \zeta_n^{-3} + \zeta_n^{3} = \alpha_3 ,\end{align*} where we’ve used that \(\zeta^{k} = \zeta^{k\operatorname{mod}n}\). From this, we see that \(\sigma_{k}(\alpha_1)=\sigma_{n-k}(\alpha_1)\) and we pick up \((n-1)/2\) distinct conjugates.
-
For \(n\) not prime, the exact same argument runs through \(\phi(n)\) values of \(k\) for \(\sigma_k\), and again yields \(\sigma_{k}(\alpha_1) = \sigma_{\phi(n) - k}(\alpha_1)\). Matching them up appropriately yields \(\phi(n)/2\) distinct roots.
Fall 2019 Midterm #10
Let \(L/K\) be a finite normal extension.
-
Show that if \(L/K\) is cyclic and \(E/K\) is normal with \(L/E/K\) then \(L/E\) and \(E/K\) are cyclic.
-
Show that if \(L/K\) is cyclic then there exists exactly one extension \(E/K\) of degree \(n\) with \(L/E/K\) for each divisor \(n\) of \([L:K]\).
The setup:
Part 1:
- \(L/K\) is cyclic means \(L/K\) is Galois and \(G\coloneqq{ \mathsf{Gal}}(L/K) = C_n\) for some \(n\).
- By the FTGT, setting \(H \coloneqq{ \mathsf{Gal}}(L/E)\), we get \(H {~\trianglelefteq~}G\) precisely because \(E/K\) is normal, and \({ \mathsf{Gal}}(L/E) = G/H\).
- But then if \(G\) is cyclic, \(H \leq G\) must be cyclic, and \(G/H\) is cyclic as well since writing \(G = C_n = \left\langle{x}\right\rangle\), we have \(G/H = \left\langle{xH}\right\rangle\).
Part 2:
-
Letting \(G\coloneqq{ \mathsf{Gal}}(L/K) = C_n\), by elementary group theory we have subgroups \(H\coloneqq C_d \leq C_n\) for every \(d\) dividing \(n\).
- A observation we’ll need: every subgroup is normal here since \(G\) is abelian.
- By the fundamental theorem, taking the fixed field of \(H \leq { \mathsf{Gal}}(L/K)\), we obtain some intermediate extension \(E\coloneqq K^H\) fitting into a tower \(L/E/K\).
- By the fundamental theorem, \([E: K] = [G:H] = n/d\), where we’ve used that \(H{~\trianglelefteq~}G\).
- Letting \(d\) range through divisors lets \(n/d\) range through divisors, so we get extensions of every degree \(d\) dividing \(n\).
Fall 2019 Midterm #8
Let \(k\) be a field of characteristic \(p\neq 0\) and \(f\in k[x]\) irreducible. Show that \(f(x) = g(x^{p^d})\) where \(g(x) \in k[x]\) is irreducible and separable.
Conclude that every root of \(f\) has the same multiplicity \(p^d\) in the splitting field of \(f\) over \(k\).
Fall 2019 Midterm #7
Show that a field \(k\) of characteristic \(p\neq 0\) is perfect \(\iff\) for every \(x\in k\) there exists a \(y\in k\) such that \(y^p=x\).
Spring 2012 #4
Let \(f(x) = x^7 - 3\in {\mathbf{Q}}[x]\) and \(E/{\mathbf{Q}}\) be a splitting field of \(f\) with \(\alpha \in E\) a root of \(f\).
-
Show that \(E\) contains a primitive 7th root of unity.
-
Show that \(E\neq {\mathbf{Q}}(\alpha)\).
Fall 2013 #5
Let \(L/K\) be a finite extension of fields.
-
Define what it means for \(L/K\) to be separable.
-
Show that if \(K\) is a finite field, then \(L/K\) is always separable.
- Give an example of a finite extension \(L/K\) that is not separable.
-
\(L/k\) is separable iff every element \(\alpha\) is separable, i.e. the minimal polynomial \(m(x)\) of \(\alpha\) is a separable polynomial, i.e. \(m(x)\) has no repeated roots in (say) the algebraic closure of \(L\) (or just any splitting field of \(m\)).
-
If \(\operatorname{ch}k = p\), suppose toward a contradiction that \(L/k\) is not separable. Then there is some \(\alpha\) with an inseparable (and irreducible) minimal polynomial \(f(x)\in k[x]\).
-
Claim: since \(f\) is inseparable and irreducible, \(f(x) = g(x^p)\) for some \(g\in k[x]\).
- Note: write \(g(x) \coloneqq\sum a_k x^k\), so that \(f(x) = \sum a_k (x^p)^k = \sum a_k x^{pk}\).
-
This is a contradiction, since it makes \(f\) reducible by using the “Freshman’s dream”: \begin{align*} f(x) = \sum a_k x^{pk} = \qty{ \sum a_k^{1\over p} x^k}^p \coloneqq(h(x))^p .\end{align*}
-
Proof of claim: in \(\operatorname{ch}k = p, f\) inseparable \(\implies f(x) = g(x^p)\).
- Use that \(f\) is inseparable iff \(\gcd(f, f') \neq 1\), and since \(f\) is irreducible this forces \(f' \equiv 0\), so \(ka_k = 0\) for all \(k\).
- Then \(a_k\neq 0\) forces \(p\divides k\), so \(f(x) = a_0 + a_px^p + a_{2p}x^{2p} + \cdots\) and one takes \(g(x) \coloneqq\sum a_{kp}x^{kp}\).
-
A finite inseparable extension:
- It’s a theorem that finite extensions of perfect fields are separable, so one needs a non-perfect field.
- Take \(L/k \coloneqq{ \mathbf{F} }_p(t^{1\over p}) / { \mathbf{F} }_p(t)\), which is a degree \(p\) extension (although both fields are infinite are characteristic \(p\)).
- Then the minimal polynomial of \(t\) is \(f(x) \coloneqq x^p - t \in { \mathbf{F} }_p(t)[x]\), where \(f'(x) = px^p \equiv 0\) Alternatively, just note that \(f\) factors as \(f(x) = (x-t^{1\over p})^p\) in \(L[x]\), which has multiple roots.
Fall 2012 #4
Let \(f(x) \in {\mathbf{Q}}[x]\) be a polynomial and \(K\) be a splitting field of \(f\) over \({\mathbf{Q}}\). Assume that \([K:{\mathbf{Q}}] = 1225\) and show that \(f(x)\) is solvable by radicals.
Galois Groups: Concrete Computations
Exercise: \(G(x^2-2)\)
Compute the Galois group of \(x^2-2\).
\({\mathbf{Z}}/2{\mathbf{Z}}\)?
Exercise: \(G(x^p-2)\)
Let \(p \in \mathbb{Z}\) be a prime number. Then describe the elements of the Galois group of the polynomial \(x^{p}-2\).
\({\mathbf{Q}}(2^{1\over p}, \zeta_p)\), which has degree \(p(p-1)\) and is generated by the maps \begin{align*} \sqrt[p]{2} & \mapsto \sqrt[p]{2} \zeta^{a} \\ \zeta & \mapsto \zeta^{b} .\end{align*}
Fall 2020 #3
-
Define what it means for a finite extension of fields \(E\) over \(F\) to be a Galois extension.
-
Determine the Galois group of \(f(x) = x^3 - 7\) over \({\mathbf{Q}}\), and justify your answer carefully.
- Find all subfields of the splitting field of \(f(x)\) over \({\mathbf{Q}}\).
Part a:
-
A finite extension \(E/F\) is Galois if it is normal and separable:
- Normal: every \(f\in F[x]\) either has no roots in \(E\) or all roots in \(E\).
- Separable: every element \(e\in E\) has a separable minimal polynomial \(m(x)\), i.e. \(m\) has no repeated roots.
Part b:
-
Note \(f\) is irreducible by Eisenstein with \(p=7\), and since \({\mathbf{Q}}\) is perfect, irreducible implies separable.
-
Writing \(L \coloneqq\operatorname{SF}(f)/{\mathbf{Q}}\), this is a Galois extension:
- \(L\) is separable: it is a finite extension of a perfect field, which is automatically separable.
- \(L\) is normal: \(L\) is the splitting field of a separable polynomial, and thus normal.
-
Since \(f\) is degree 3, we have \(G\coloneqq{ \mathsf{Gal}}(L/k) \leq S_3\), and since \(G\) is a transitive subgroup the only possibilities are \begin{align*} G = S_3 \cong D_3, A_3 \cong C_3 .\end{align*}
-
Factor \(x^3 - 7 = (x-\omega)(x-\zeta_3\omega)(x-\zeta_3^2\omega)\) where \(\omega \coloneqq 7^{1\over 3}\) and \(\zeta_3\) is a primitive 3rd root of unity. Then \(L = {\mathbf{Q}}(\zeta_3, \omega)\).
- Aside: label the roots in this order, so \(r_1 = \omega, r_2 = \zeta_3\omega, r_3 = \zeta_3^2\omega\).
-
Write \(\min_{\omega, {\mathbf{Q}}}(x) = x^3 - 7\) and let \(L_0/{\mathbf{Q}}\coloneqq{\mathbf{Q}}(\omega)/{\mathbf{Q}}\) yields \([L_0: {\mathbf{Q}}] = 3\).
-
Write \(\min_{\zeta_3, {\mathbf{Q}}}(x) = (x^3-1)/(x-1) = x^2 + x + 1\), and note that this is still the minimal polynomial over \(L_0\) since \(L_0 \subseteq {\mathbf{R}}\) and \(\zeta_3 \in {\mathbf{C}}\setminus{\mathbf{R}}\). So \([L:L_0] = 2\).
-
Counting in towers, \begin{align*} [L:{\mathbf{Q}}] = [L:L_0][L_0: {\mathbf{Q}}] = (2)(3) = 6 .\end{align*}
-
But \({\sharp}S_3 = 6\) and \({\sharp}A_3 = 3\), so \(G = S_3\).
-
Explicitly, since we can write \(\operatorname{SF}(f) = {\mathbf{Q}}(\omega, \zeta_3)\), we can find explicit generators: \begin{align*} \sigma: &\begin{cases} \omega &\mapsto \omega \\ \zeta_3 &\mapsto \zeta_3\cdot \zeta_3. \end{cases} && \implies \sigma \sim (1,2,3) \\ \tau: &\begin{cases} \omega &\mapsto \omega \\ \zeta_3 &\mapsto \mkern 1.5mu\overline{\mkern-1.5mu\zeta_3\mkern-1.5mu}\mkern 1.5mu. \end{cases} && \implies \tau \sim (2, 3) .\end{align*} So \(G = \left\langle{\sigma, \tau {~\mathrel{\Big\vert}~}\sigma^3, \tau^2}\right\rangle\).
Part c:
- Note that the subgroup lattice for \(S_3\) looks like the following:
-
Note that we can identify
- \(\tau = (2,3)\) which fixes \(r_1\)
- \(\sigma \tau = (1,2)\) which fixes \(r_3\)
- \(\sigma^2\tau = (1, 3)\) which fixes \(r_2\)
- \(\sigma = (1,2,3)\), for which we need to calculate the fixed field. Using that \(\sigma(\omega) =\zeta\omega\) and \(\sigma(\zeta)=\zeta\), supposing \(\sigma(\alpha) = \alpha\) we have \begin{align*} \sigma(\alpha) &\coloneqq\sigma(a + b\zeta_3 + c\zeta_3^2 + d\omega + e\zeta_3\omega + f\zeta_3^2\omega) \\ &= a + b\zeta_3 + c\zeta_3^2 + d\zeta_3\omega + e\zeta_3^2\omega + f\omega \\ \implies \alpha &= a + b\zeta_3 + c\zeta_3^2 + t_1(\omega + \zeta_3\omega + \zeta_3^2\omega) \\ \implies \alpha &= a + b\zeta_3 + c\zeta_3^2 + t_1\omega (1 + \zeta_3+ \zeta_3^2) \\ \implies \alpha &= a + b\zeta_3 + c\zeta_3^2 ,\end{align*} using the general fact that \(\sum_{k=0}^{n-1}\zeta_n^k = 0\). So the fixed field is \({\mathbf{Q}}(1, \zeta, \zeta^2) = {\mathbf{Q}}(\zeta)\).
- We thus get the following lattice correspondence:
Spring 2021 #4
Define \begin{align*} f(x) \coloneqq x^4 + 4x^2 + 64 \in {\mathbf{Q}}[x] .\end{align*}
-
Find the splitting field \(K\) of \(f\) over \({\mathbf{Q}}\).
-
Find the Galois group \(G\) of \(f\).
- Exhibit explicitly the correspondence between subgroups of \(G\) and intermediate fields between \({\mathbf{Q}}\) and \(K\).
- Useful trick: given \(a + \sqrt{b}\), try to rewrite this as \((\sqrt{c} + \sqrt{d})^2\) for some \(c, d\) to get a better basis for \(\operatorname{SF}(f)\).
-
First consider \(g(z) \coloneqq z^2 + 4z + 64\). Applying the quadratic formula yields \begin{align*} z = {-4 \pm \sqrt{16 - 64} \over 2} = -2 \pm {1\over 2}\sqrt{ -15 \cdot 16 } = -2 \pm 2i \sqrt{15} .\end{align*}
-
Substituting \(z=x^2\) yields the splitting field of \(f\) as \(L\coloneqq{\mathbf{Q}}(\pm \sqrt{ -2 \pm 2i\sqrt{15}})\).
- Note that this factorization shows that \(f\) is irreducible over \({\mathbf{Q}}\), since the two quadratic factors have irrational coefficients and none of the roots are real.
- Irreducible implies separable over a perfect field, so \(L/{\mathbf{Q}}\) is a separable extension.
- \(L\) is the splitting field of a separable polynomial and thus normal, making \(L\) Galois.
-
In this form, it’s not clear what the degree \([L:{\mathbf{Q}}]\) is, so we can find a better basis by rewriting the roots of \(g\): \begin{align*} z = -2 \pm 2i\sqrt{15} = \qty{\sqrt{5}}^2 - \qty{\sqrt 3}^2 \pm 2i\sqrt{5}\sqrt{3} = (\sqrt 5 \pm i\sqrt{3})^2 ,\end{align*} and so the roots of \(f\) are \(x = \pm \sqrt{5} \pm i\sqrt{3}\) and \(L = {\mathbf{Q}}(\sqrt 5, i\sqrt 3)\).
-
Counting in towers, \begin{align*} [L:{\mathbf{Q}}] = [{\mathbf{Q}}(\sqrt 5, i \sqrt{3} ) : {\mathbf{Q}}\sqrt{5} ][{\mathbf{Q}}\sqrt{5} : {\mathbf{Q}}] = (2)(2) = 4 ,\end{align*} where we’ve used that \(\min_{\sqrt 5, {\mathbf{Q}}}(x) = x^2-5\) and \(\min_{i\sqrt 3, {\mathbf{Q}}}(x) = x^2 + 3\), which remains the minimal polynomial over \({\mathbf{Q}}(\sqrt 5) \subseteq {\mathbf{R}}\) since both roots are not real.
-
So \(G\coloneqq{ \mathsf{Gal}}(L/{\mathbf{Q}}) \leq S_4\) is a transitive subgroup of size 4, making it either \(C_4\) or \(C_2^2\).
-
Label the roots: \begin{align*} r_1 &= \sqrt 5 + i\sqrt 3 \\ r_2 &= \sqrt{5} - i \sqrt{3} \\ r_3 &= - \sqrt 5 + i\sqrt 3 = -r_2 \\ r_4 &= -\sqrt{5} - i\sqrt{3} = -r_1 .\end{align*}
-
We can start writing down automorphisms: \begin{align*} \sigma_1: \begin{cases} \sqrt 5 &\mapsto -\sqrt 5 \\ i\sqrt 3 &\mapsto i\sqrt 3 . \end{cases} && \sigma_1 \sim (1,3)(2,4) \\ \sigma_2 \begin{cases} \sqrt 5 &\mapsto \sqrt 5 \\ i\sqrt 3 &\mapsto -i\sqrt 3 . \end{cases} && \sigma_2 \sim (1, 2)(3, 4) .\end{align*} Note that these define automorphisms because we’ve specified what happens to a basis and they send roots to other roots.
-
Checking that \(\sigma_1^2 = \sigma_2^2 = \operatorname{id}\), this produces two distinct order 2 elements, forcing \(G \cong C_2^2\) since \(C_4\) only has one order 2 element. Explicitly, we have \begin{align*} C_2^2 \cong G = \left\langle{\tau_1, \tau_2}\right\rangle = \left\{{\operatorname{id}, \tau_1, \tau_2, \tau_1 \tau_2}\right\} = \left\{{\operatorname{id}, (1,3)(2,4), (1,2)(3,4), (1,4)(2,3) }\right\} ,\end{align*} and the generic subgroup lattice looks like:
-
Computing some fixed fields. Write \(i \sqrt{3} = x, \sqrt{5} = y\), then elements in the splitting field are of the form \(\alpha = 1 + ax + by + cxy\).
-
For \(\sigma_1\), we have \(x\mapsto -x\), so \begin{align*} \sigma_1(\alpha) = 1 - ax + by - cxy = \alpha \implies a=-a=0, c=-c=0 ,\end{align*} so this preserves \(1+by\), making the fixed field \({\mathbf{Q}}(1, y) = {\mathbf{Q}}(i \sqrt{3})\).
-
For \(\sigma_2\), we have \(y\mapsto -y\), so \begin{align*} \sigma_2(\alpha) = 1 +ax -by -cxy = \alpha \implies b=-b=0,c=-c=0 ,\end{align*} preserving \(1 + ax\) and making the fixed field \({\mathbf{Q}}(1, x) = {\mathbf{Q}}(\sqrt 5)\).
-
For \(\sigma_1 \sigma_2\), we have \(x\mapsto -x\) and \(y\mapsto -y\), so \begin{align*} \sigma_1\sigma_2(\alpha) = 1 -ax -by +cxy = \alpha \implies a=-a=-, b=-b=0 ,\end{align*} preserving \(1 + cxy\) and yielding \({\mathbf{Q}}(xy) = {\mathbf{Q}}(i\sqrt 3 \sqrt 5)\).
-
-
So the lattice correspondence we get here is
Fall 2019 Midterm #6
Compute the Galois group of \(f(x) = x^3-3x -3\in {\mathbf{Q}}[x]/{\mathbf{Q}}\).
Spring 2018 #2
Let \(f(x) = x^4 - 4x^2 + 2 \in {\mathbf{Q}}[x]\).
-
Find the splitting field \(K\) of \(f\), and compute \([K: {\mathbf{Q}}]\).
-
Find the Galois group \(G\) of \(f\), both as an explicit group of automorphisms, and as a familiar abstract group to which it is isomorphic.
- Exhibit explicitly the correspondence between subgroups of \(G\) and intermediate fields between \({\mathbf{Q}}\) and \(k\).
\todo[inline]{Not the nicest proof! Would be better to replace the ad-hoc computations at the end.}
Note that \(g(x) = x^2 - 4x + 2\) has roots \(\beta = 2 \pm \sqrt{2}\), and so \(f\) has roots \begin{align*} \alpha_1 &= \sqrt{2 + \sqrt 2} \\ \alpha_2 &= \sqrt{2 - \sqrt 2} \\ \alpha_3 &= -\alpha_1 \\ \alpha_4 &= -\alpha_2 .\end{align*}
and splitting field \(K = {\mathbf{Q}}(\left\{{\alpha_i}\right\})\).
\(K\) is the splitting field of a separable polynomial and thus Galois over \({\mathbf{Q}}\). Moreover, Since \(f\) is irreducible by Eisenstein with \(p=2\), the Galois group is a transitive subgroup of \(S^4\), so the possibilities are:
- \(S_4\)
- \(A_4\)
- \(D_4\)
- \({\mathbf{Z}}/(2) \times{\mathbf{Z}}/(2)\)
- \({\mathbf{Z}}/(4)\)
We can note that \(g\) splits over \(L \coloneqq{\mathbf{Q}}(\sqrt 2)\), an extension of degree 2.
We can now note that \(\min(\alpha, L)\) is given by \(p(x) = x^2 - (2 + \sqrt 2)\), and so \([K: L] = 2\).
We then have \begin{align*} [K: {\mathbf{Q}}] = [K: L] [L : {\mathbf{Q}}] = (2)(2) = 4 .\end{align*}
This \({\left\lvert {{ \mathsf{Gal}}(K/{\mathbf{Q}})} \right\rvert} = 4\), which leaves only two possibilities:
- \({\mathbf{Z}}/(2) \times{\mathbf{Z}}/(2)\)
- \({\mathbf{Z}}/(4)\)
We can next check orders of elements. Take \begin{align*} \sigma &\in { \mathsf{Gal}}(K/{\mathbf{Q}}) \\ \alpha_1 &\mapsto \alpha_2 .\end{align*}
Computations show that
- \(\alpha_1^2 \alpha_2^2 = 2\), so \(\alpha_1 \alpha_2 = \sqrt 2\)
- \(\alpha_1^2 = 2 + \sqrt 2 \implies \sqrt 2 = \alpha_1^2 - 2\)
and thus \begin{align*} \sigma^2(\alpha_1) &= \sigma(\alpha_2) \\ &= \sigma\left(\frac{\sqrt 2}{\alpha_1}\right) \\ &= \frac{\sigma(\sqrt 2)}{\sigma(\alpha_1)} \\ &= \frac{\sigma(\alpha_1^2 - 2)}{\alpha_2} \\ &= \frac{\alpha_2^2 - 2}{\alpha_2} \\ &= \alpha_2 -2\alpha_2^{-1}\\ &= \alpha_2 - \frac{2\alpha_1}{\sqrt 2} \\ &= \alpha_2 -\alpha_1 \sqrt 2 \\ &\neq \alpha_1 ,\end{align*}
and so the order of \(\sigma\) is strictly greater than 2, and thus 4, and thus \({ \mathsf{Gal}}(K/{\mathbf{Q}}) = \left\{{\sigma^k {~\mathrel{\Big\vert}~}1\leq k \leq 4}\right\} \cong {\mathbf{Z}}/(4)\).
?? The subgroup of index 2 \(\left\langle{\sigma^2}\right\rangle\) corresponds to the field extension \(Q(\sqrt 2) / {\mathbf{Q}}\).
\todo[inline]{Finish (c)}
Spring 2020 #4
Let \(f(x) = x^4-2 \in {\mathbf{Q}}[x]\).
-
Define what it means for a finite extension field \(E\) of a field \(F\) to be a Galois extension.
-
Determine the Galois group \({ \operatorname{Gal}}(E/{\mathbf{Q}})\) for the polynomial \(f(x)\), and justify your answer carefully.
- Exhibit a subfield \(K\) in \((b)\) such that \({\mathbf{Q}}\leq K \leq E\) with \(K\) not a Galois extension over \({\mathbf{Q}}\). Explain.
Spring 2017 #8
-
Let \(K\) denote the splitting field of \(x^5 - 2\) over \({\mathbf{Q}}\). Show that the Galois group of \(K/{\mathbf{Q}}\) is isomorphic to the group of invertible matrices \begin{align*} \left(\begin{array}{ll} a & b \\ 0 & 1 \end{array}\right) {\quad \operatorname{where} \quad} a\in { \mathbf{F} }_5^{\times}\text{ and } b\in { \mathbf{F} }_5 .\end{align*}
-
Determine all intermediate fields between \(K\) and \({\mathbf{Q}}\) which are Galois over \({\mathbf{Q}}\).
Fall 2016 #4
Set \(f(x) = x^3 - 5 \in {\mathbf{Q}}[x]\).
-
Find the splitting field \(K\) of \(f(x)\) over \({\mathbf{Q}}\).
-
Find the Galois group \(G\) of \(K\) over \({\mathbf{Q}}\).
- Exhibit explicitly the correspondence between subgroups of \(G\) and intermediate fields between \({\mathbf{Q}}\) and \(K\).
Spring 2016 #2
Let \(K = {\mathbf{Q}}[\sqrt 2 + \sqrt 5]\).
-
Find \([K: {\mathbf{Q}}]\).
-
Show that \(K/{\mathbf{Q}}\) is Galois, and find the Galois group \(G\) of \(K/{\mathbf{Q}}\).
- Exhibit explicitly the correspondence between subgroups of \(G\) and intermediate fields between \({\mathbf{Q}}\) and \(K\).
Fall 2015 #5
Let \(u = \sqrt{2 + \sqrt{2}}\), \(v = \sqrt{2 - \sqrt{2}}\), and \(E = {\mathbf{Q}}(u)\).
-
Find (with justification) the minimal polynomial \(f(x)\) of \(u\) over \({\mathbf{Q}}\).
-
Show \(v\in E\), and show that \(E\) is a splitting field of \(f(x)\) over \({\mathbf{Q}}\).
- Determine the Galois group of \(E\) over \({\mathbf{Q}}\) and determine all of the intermediate fields \(F\) such that \({\mathbf{Q}}\subset F \subset E\).
Spring 2015 #5
Let \(f(x) = x^4 - 5 \in {\mathbf{Q}}[x]\).
-
Compute the Galois group of \(f\) over \({\mathbf{Q}}\).
-
Compute the Galois group of \(f\) over \({\mathbf{Q}}(\sqrt{5})\).
Fall 2014 #3
Consider the polynomial \(f(x) = x^4 - 7 \in {\mathbf{Q}}[x]\) and let \(E/{\mathbf{Q}}\) be the splitting field of \(f\).
-
What is the structure of the Galois group of \(E/{\mathbf{Q}}\)?
-
Give an explicit description of all of the intermediate subfields \({\mathbf{Q}}\subset K \subset E\) in the form \(K = {\mathbf{Q}}(\alpha), {\mathbf{Q}}(\alpha, \beta), \cdots\) where \(\alpha, \beta\), etc are complex numbers. Describe the corresponding subgroups of the Galois group.
Fall 2013 #6
Let \(K\) be the splitting field of \(x^4-2\) over \({\mathbf{Q}}\) and set \(G = { \operatorname{Gal}}(K/{\mathbf{Q}})\).
-
Show that \(K/{\mathbf{Q}}\) contains both \({\mathbf{Q}}(i)\) and \({\mathbf{Q}}(\sqrt[4]{2})\) and has degree 8 over \({\mathbf{Q}}\)/
-
Let \(N = { \operatorname{Gal}}(K/{\mathbf{Q}}(i))\) and \(H = { \operatorname{Gal}}(K/{\mathbf{Q}}(\sqrt[4]{2}))\). Show that \(N\) is normal in \(G\) and \(NH = G\).
Hint: what field is fixed by \(NH\)?
-
Show that \({ \operatorname{Gal}}(K/{\mathbf{Q}})\) is generated by elements \(\sigma, \tau\), of orders 4 and 2 respectively, with \(\tau \sigma\tau^{-1}= \sigma^{-1}\).
Equivalently, show it is the dihedral group of order 8.
-
How many distinct quartic subfields of \(K\) are there? Justify your answer.
Spring 2014 #4
Let \(E\subset {\mathbf{C}}\) denote the splitting field over \({\mathbf{Q}}\) of the polynomial \(x^3 - 11\).
-
Prove that if \(n\) is a squarefree positive integer, then \(\sqrt{n}\not\in E\).
Hint: you can describe all quadratic extensions of \({\mathbf{Q}}\) contained in \(E\).
-
Find the Galois group of \((x^3 - 11)(x^2 - 2)\) over \({\mathbf{Q}}\).
- Prove that the minimal polynomial of \(11^{1/3} + 2^{1/2}\) over \({\mathbf{Q}}\) has degree 6.
Spring 2013 #8
Let \(F\) be the field with 2 elements and \(K\) a splitting field of \(f(x) = x^6 + x^3 + 1\) over \(F\). You may assume that \(f\) is irreducible over \(F\).
-
Show that if \(r\) is a root of \(f\) in \(K\), then \(r^9 = 1\) but \(r^3\neq 1\).
-
Find \({ \operatorname{Gal}}(K/F)\) and express each intermediate field between \(F\) and \(K\) as \(F(\beta)\) for an appropriate \(\beta \in K\).
Galois Groups: Indirect Computations / Facts
Fall 2019 #7
Let \(\zeta_n\) denote a primitive \(n\)th root of 1 \(\in {\mathbf{Q}}\). You may assume the roots of the minimal polynomial \(p_n(x)\) of \(\zeta_n\) are exactly the primitive \(n\)th roots of 1.
Show that the field extension \({\mathbf{Q}}(\zeta_n )\) over \({\mathbf{Q}}\) is Galois and prove its Galois group is \(({\mathbf{Z}}/n{\mathbf{Z}})^{\times}\).
How many subfields are there of \({\mathbf{Q}}(\zeta_{20} )\)?
-
Galois = normal + separable.
-
Separable: Minimal polynomial of every element has distinct roots.
-
Normal (if separable): Splitting field of an irreducible polynomial.
-
\(\zeta\) is a primitive root of unity \(\iff o(\zeta) = n\) in \({ \mathbf{F} }^{\times}\).
-
\(\phi(p^k) = p^{k-1}(p-1)\)
-
The lattice:
Let \(K = {\mathbf{Q}}(\zeta)\). Then \(K\) is the splitting field of \(f(x) = x^n - 1\), which is irreducible over \({\mathbf{Q}}\), so \(K/{\mathbf{Q}}\) is normal. We also have \(f'(x) = nx^{n-1}\) and \(\gcd(f, f') = 1\) since they can not share any roots.
Or equivalently, \(f\) splits into distinct linear factors \(f(x) = \prod_{k\leq n}(x-\zeta^k)\).
Since it is a Galois extension, \({\left\lvert {{ \mathsf{Gal}}(K/{\mathbf{Q}})} \right\rvert} = [K: {\mathbf{Q}}] = \phi(n)\) for the totient function.
We can now define maps \begin{align*} \tau_j: K &\to K \\ \zeta &\mapsto \zeta^j \end{align*} and if we restrict to \(j\) such that \(\gcd(n, j) = 1\), this yields \(\phi(n)\) maps. Noting that if \(\zeta\) is a primitive root, then \((n, j) = 1\) implies that that \(\zeta^j\) is also a primitive root, and hence another root of \(\min(\zeta, {\mathbf{Q}})\), and so these are in fact automorphisms of \(K\) that fix \({\mathbf{Q}}\) and thus elements of \({ \mathsf{Gal}}(K/{\mathbf{Q}})\).
So define a map \begin{align*} \theta: {\mathbf{Z}}_n^{\times}&\to K \\ [j]_n &\mapsto \tau_j .\end{align*}
from the multiplicative group of units to the Galois group.
The claim is that this is a surjective homomorphism, and since both groups are the same size, an isomorphism.
Letting \(\sigma \in K\) be arbitrary, noting that \([K: {\mathbf{Q}}]\) has a basis \(\left\{{1, \zeta, \zeta^2, \cdots, \zeta^{n-1}}\right\}\), it suffices to specify \(\sigma(\zeta)\) to fully determine the automorphism. (Since \(\sigma(\zeta^k) = \sigma(\zeta)^k\).)
In particular, \(\sigma(\zeta)\) satisfies the polynomial \(x^n - 1\), since \(\sigma(\zeta)^n = \sigma(\zeta^n) = \sigma(1) = 1\), which means \(\sigma(\zeta)\) is another root of unity and \(\sigma(\zeta) = \zeta^k\) for some \(1\leq k \leq n\).
Moreover, since \(o(\zeta) = n \in K^{\times}\), we must have \(o(\zeta^k) = n \in K^{\times}\) as well. Noting that \(\left\{{\zeta^i}\right\}\) forms a cyclic subgroup \(H\leq K^{\times}\), then \(o(\zeta^k) = n \iff (n, k) = 1\) (by general theory of cyclic groups).
Thus \(\theta\) is surjective.
\begin{align*} \tau_j \circ \tau_k (\zeta) =\tau_j(\zeta^k) = \zeta^{jk} \implies \tau_{jk} = \theta(jk) = \tau_j \circ \tau_k .\end{align*}
We have \(K \cong {\mathbf{Z}}_{20}^{\times}\) and \(\phi(20) = 8\), so \(K \cong {\mathbf{Z}}_8\), so we have the following subgroups and corresponding intermediate fields:
- \(0 \sim {\mathbf{Q}}(\zeta_{20})\)
- \({\mathbf{Z}}_2 \sim {\mathbf{Q}}(\omega_1)\)
- \({\mathbf{Z}}_4 \sim {\mathbf{Q}}(\omega_2)\)
- \({\mathbf{Z}}_8 \sim {\mathbf{Q}}\)
For some elements \(\omega_i\) which exist by the primitive element theorem.
Fall 2018 #3
Let \(F \subset K \subset L\) be finite degree field extensions. For each of the following assertions, give a proof or a counterexample.
-
If \(L/F\) is Galois, then so is \(K/F\).
-
If \(L/F\) is Galois, then so is \(L/K\).
- If \(K/F\) and \(L/K\) are both Galois, then so is \(L/F\).
- Every quadratic extension over \({\mathbf{Q}}\) is Galois.
Let \(L/K/F\).
False: Take \(L/K/F = {\mathbf{Q}}(\zeta_2, \sqrt[3] 2) \to {\mathbf{Q}}(\sqrt[3] 2) \to {\mathbf{Q}}\).
Then \(L/F\) is Galois, since it is the splitting field of \(x^3 - 2\) and \({\mathbf{Q}}\) has characteristic zero.
But \(K/F\) is not Galois, since it is not the splitting field of any irreducible polynomial.
True: If \(L/F\) is Galois, then \(L/K\) is normal and separable:
-
\(L/K\) is normal, since if \(\sigma: L \hookrightarrow\overline K\) lifts the identity on \(K\) and fixes \(L\), i-t also lifts the identity on \(F\) and fixes \(L\) (and \(\overline K = \overline F\)).
-
\(L/K\) is separable, since \(F[x] \subseteq K[x]\), and so if \(\alpha \in L\) where \(f(x) \coloneqq\min(\alpha, F)\) has no repeated factors, then \(f'(x) \coloneqq\min(\alpha, K)\) divides \(f\) and thus can not have repeated factors.
False: Use the fact that every quadratic extension is Galois, and take \(L/K/F = {\mathbf{Q}}(\sqrt[4] 2) \to {\mathbf{Q}}(\sqrt 2) \to {\mathbf{Q}}\).
Then each successive extension is quadratic (thus Galois) but \({\mathbf{Q}}(\sqrt[4] 2)\) is not the splitting field of any polynomial (noting that it does not split \(x^4 - 2\) completely.)
Spring 2018 #3
Let \(K\) be a Galois extension of \({\mathbf{Q}}\) with Galois group \(G\), and let \(E_1 , E_2\) be intermediate fields of \(K\) which are the splitting fields of irreducible \(f_i (x) \in {\mathbf{Q}}[x]\).
Let \(E = E_1 E_2 \subset K\).
Let \(H_i = { \mathsf{Gal}}(K/E_i)\) and \(H = { \mathsf{Gal}}(K/E)\).
-
Show that \(H = H_1 \cap H_2\).
-
Show that \(H_1 H_2\) is a subgroup of \(G\).
- Show that \begin{align*} { \mathsf{Gal}}(K/(E_1 \cap E_2 )) = H_1 H_2 .\end{align*}
-
The Galois correspondence:
- \(H_1 \cap H_2 \rightleftharpoons E_1 E_2\),
- \(H_1 H_2 \rightleftharpoons E_1 \cap E_2\).
By the Galois correspondence, it suffices to show that the fixed field of \(H_1 \cap H_2\) is \(E_1 E_2\).
Let \(\sigma \in H_1 \cap H_2\); then \(\sigma \in \mathop{\mathrm{Aut}}(K)\) fixes both \(E_1\) and \(E_2\).
Not sure if this works – compositum is not literally product..?
Writing \(x \in E_1E_2\) as \(x=e_1 e_2\), we have \begin{align*} \sigma(x) = \sigma(e_1 e_2) = \sigma(e_1) \sigma(e_2) = e_1 e_2 =x, \end{align*}
so \(\sigma\) fixes \(E_1 E_2\).
That \(H_1 H_2 \subseteq G\) is clear, since if \(\sigma = \tau_1 \tau_2 \in H_1 H_2\), then each \(\tau_i\) is an automorphism of \(K\) that fixes \(E_i \supseteq {\mathbf{Q}}\), so each \(\tau_i\) fixes \({\mathbf{Q}}\) and thus \(\sigma\) fixes \({\mathbf{Q}}\).
All elements in this subset commute.
-
Let \(\sigma = \sigma_1 \sigma_2 \in H_1 H_2\).
-
Note that \(\sigma_1(e) = e\) for all \(e\in E_1\) by definition, since \(H_1\) fixes \(E_1\), and \(\sigma_2(e) \in E_1\) (?).
-
Then \begin{align*} \sigma_1(e) = e \quad \forall e \in E_1 \implies \sigma_1(\sigma_2(e)) = \sigma_2(e) \end{align*} and substituting \(e = \sigma_1(e)\) on the RHS yields \begin{align*} \sigma_1 \sigma_2(e) = \sigma_2 \sigma_1(e) ,\end{align*} where a similar proof holds for \(e\in E_2\) and thus for arbitrary \(x\in E_1 E_2\).
By the Galois correspondence, the subgroup \(H_1H_2 \leq G\) will correspond to an intermediate field \(E\) such that \(K/E/{\mathbf{Q}}\) and \(E\) is the fixed field of \(H_1 H_2\).
But if \(\sigma \in H_1 H_2\), then \(\sigma = \tau_1 \tau_2\) where \(\tau_i\) is an automorphism of \(K\) that fixes \(E_i\), and so \begin{align*} \sigma(x) = x \iff \tau_1\tau_2(x) = x &\iff \tau_2(x) = x \\ &~\&~ \\ \tau_1(x) = x &\iff x \in E_1 \cap E_2 .\end{align*} .
Fall 2017 #4
-
Let \(f (x)\) be an irreducible polynomial of degree 4 in \({\mathbf{Q}}[x]\) whose splitting field \(K\) over \({\mathbf{Q}}\) has Galois group \(G = S_4\).
Let \(\theta\) be a root of \(f(x)\). Prove that \({\mathbf{Q}}[\theta]\) is an extension of \({\mathbf{Q}}\) of degree 4 and that there are no intermediate fields between \({\mathbf{Q}}\) and \({\mathbf{Q}}[\theta]\).
-
Prove that if \(K\) is a Galois extension of \({\mathbf{Q}}\) of degree 4, then there is an intermediate subfield between \(K\) and \({\mathbf{Q}}\).
Spring 2017 #7
Let \(F\) be a field and let \(f(x) \in F[x]\).
-
Define what a splitting field of \(f(x)\) over \(F\) is.
-
Let \(F\) now be a finite field with \(q\) elements. Let \(E/F\) be a finite extension of degree \(n>0\). Exhibit an explicit polynomial \(g(x) \in F[x]\) such that \(E/F\) is a splitting field of \(g(x)\) over \(F\). Fully justify your answer.
- Show that the extension \(E/F\) in (b) is a Galois extension.
Spring 2016 #6
Let \(K\) be a Galois extension of a field \(F\) with \([K: F] = 2015\). Prove that \(K\) is an extension by radicals of the field \(F\).
Fall 2015 #6
-
Let \(G\) be a finite group. Show that there exists a field extension \(K/F\) with \({ \operatorname{Gal}}(K/F) = G\).
You may assume that for any natural number \(n\) there is a field extension with Galois group \(S_n\).
-
Let \(K\) be a Galois extension of \(F\) with \({\left\lvert {{ \operatorname{Gal}}(K/F)} \right\rvert} = 12\). Prove that there exists an intermediate field \(E\) of \(K/F\) with \([E: F] = 3\).
- With \(K/F\) as in (b), does an intermediate field \(L\) necessarily exist satisfying \([L: F] = 2\)? Give a proof or counterexample.
Fall 2014 #1
Let \(f\in {\mathbf{Q}}[x]\) be an irreducible polynomial and \(L\) a finite Galois extension of \({\mathbf{Q}}\). Let \(f(x) = g_1(x)g_2(x)\cdots g_r(x)\) be a factorization of \(f\) into irreducibles in \(L[x]\).
-
Prove that each of the factors \(g_i(x)\) has the same degree.
-
Give an example showing that if \(L\) is not Galois over \({\mathbf{Q}}\), the conclusion of part (a) need not hold.
Spring 2013 #7
Let \(f(x) = g(x) h(x) \in {\mathbf{Q}}[x]\) and \(E,B,C/{\mathbf{Q}}\) be the splitting fields of \(f,g,h\) respectively.
-
Prove that \({ \operatorname{Gal}}(E/B)\) and \({ \operatorname{Gal}}(E/C)\) are normal subgroups of \({ \operatorname{Gal}}(E/{\mathbf{Q}})\).
-
Prove that \({ \operatorname{Gal}}(E/B) \cap{ \operatorname{Gal}}(E/C) = \left\{{1}\right\}\).
-
If \(B\cap C = {\mathbf{Q}}\), show that \({ \operatorname{Gal}}(E/B) { \operatorname{Gal}}(E/C) = { \operatorname{Gal}}(E/{\mathbf{Q}})\).
-
Under the hypothesis of (c), show that \({ \operatorname{Gal}}(E/{\mathbf{Q}}) \cong { \operatorname{Gal}}(E/B) \times { \operatorname{Gal}}(E/C)\).
- Use (d) to describe \({ \operatorname{Gal}}({\mathbf{Q}}[\alpha]/{\mathbf{Q}})\) where \(\alpha = \sqrt 2 + \sqrt 3\).
Fall 2012 #3
Let \(f(x) \in {\mathbf{Q}}[x]\) be an irreducible polynomial of degree 5. Assume that \(f\) has all but two roots in \({\mathbf{R}}\). Compute the Galois group of \(f(x)\) over \({\mathbf{Q}}\) and justify your answer.
\(p\)th Roots and \(x^{p^k}-x\)
Spring 2021 #7
Let \(p\) be a prime number and let \(F\) be a field of characteristic \(p\). Show that if \(a\in F\) is not a \(p\)th power in \(F\), then \(x^p-a \in F[x]\) is irreducible.
- Contradiction: go to splitting field, apply Freshman’s dream.
- Use that this polynomial is ramified, and its only factors are \((x-a)\).
- Suppose \(a\) is not a \(p\)th power in \(F\), then \(f(x) \coloneqq x^p-a\) has no roots in \(F\).
- Toward a contradiction, suppose \(f\) is reducible in \(F[x]\).
-
In \(\operatorname{SF}(f)\), since \(\operatorname{ch}F = p\) we have \(f(x) = (x-\zeta)^p\) for some \(\zeta = a^{1\over p}\).
- So if \(f\) is reducible in \(F[x]\), we have \(f(x) = p_1(x) p_2(x)\) where \(p(x) = (x-\zeta)^q\in F[x]\) for some \(1\leq q < p\), since these are the only factors of \(f\).
- The claim is that \(\zeta\in F\) as well, which is a contradiction since \(\zeta\) is a \(p\)th root of \(a\).
- We have \(x^q-\zeta^q \in F[x]\), so \(\zeta^q\in F\).
-
We know \(a = \zeta^p\in F\), and thus \(\zeta^{d} = \zeta\in F\) for \(d \coloneqq\gcd(p, n) = 1\). \(\contradiction\)
- Why this is true: write \(d = \gcd(p, n)\) in \({\mathbf{Z}}\) to obtain \(d = tp + sn\) for some \(t, s\).
- Then \(\zeta^d = \zeta^{tp+sn} = (\zeta^p)^t \cdot (\zeta^n)^s \in F\).
- By contrapositive, show that \(f(x) \coloneqq x^p-a \in { \mathbf{F} }[x]\) reducible \(\implies a\) is a \(p\)th power in \({ \mathbf{F} }\).
- Eventually show \(a^\ell = b^p\) for some \(\ell\in {\mathbb{N}}\) and some \(b\in { \mathbf{F} }\), then \(\gcd(\ell, p) = 1\) forces \(b=a\) and \(\ell=p\).
- Use the fact that the constant term of any \(g\in { \mathbf{F} }[x]\) is actually in \({ \mathbf{F} }\).
-
Reducible: \(f\in { \mathbf{F} }[x]\) is reducible iff there exists \(g, h\in { \mathbf{F} }[x]\) nonconstant with \(f = g h\).
- Importantly, this factorization needs to happen in \({ \mathbf{F} }[x]\), since we can always find such factorizations in the splitting field \(\operatorname{SF}(f)[x]\).
- Bezout’s identity: \(\gcd(p, q) = d \implies\) there exist \(s,t\in {\mathbf{Z}}\) such that \begin{align*} sp + tq = d .\end{align*}
-
WTS: \(f(x) \coloneqq x^p - a\in { \mathbf{F} }[x]\) reducible \(\implies f\) has a root in the base field \({ \mathbf{F} }\).
-
Write \(f(x) = g(x) h(x)\) and factor \(f(x) = \prod_{i=1}^p (x- r_i) \in \operatorname{SF}(f)[x]\) where the \(r_i\) are not necessarily distinct roots.
-
WLOG, \(g(x) = \prod_{i=1}^\ell (x-r_i)\) for some \(1\leq \ell \leq p-1\), i.e. rearrange the factors so that \(g\) is the first \(\ell\) of them.
- \(\ell \neq 1, p\) since \(f\) is reducible, making \(g, h\) nonconstant.
-
Set \(R_\ell \coloneqq\prod_{i=1}^\ell r_i\), which is the constant term in \(g\), so \(R_\ell \in { \mathbf{F} }\) since \(g\in { \mathbf{F} }[x]\).
-
Each \(r_i\) is a root of \(f\), so \(r_i^p - a = 0\) for all \(i\), so \(r_i^p = a\).
-
Trick: what is the \(p\)th power of \(R_\ell\)? \begin{align*} R_\ell^p &\coloneqq\qty{ \prod_{i=1}^\ell}^p \\ &= \prod_{i=1}^\ell r_i^p \\ &= \prod_{i=1}^\ell a \\ &= a^\ell ,\end{align*} so \(R_\ell^p = a^\ell\).
-
Use Bezout: \(\gcd(\ell, p) = 1\) since \(p\) is prime, so write \(tp + s\ell = 1\) for some \(t,s\in {\mathbf{Z}}\)
-
Use this to build a root of \(f\) that’s in \({ \mathbf{F} }\): write \begin{align*} a &= a^1\\ &= a^{tp + s\ell} \\ &= a^{tp} a^{s\ell} \\ &=a^{tp} (a^\ell)^s\\ &= a^{tp} (R_\ell^p)^s \\ &= (a^t R_\ell^s)^p \\ &\coloneqq\beta^p ,\end{align*} so \(a = \beta^p\).
- Check \(\beta\in { \mathbf{F} }\): use that \(R_\ell \in { \mathbf{F} }\) since it was a constant term of a polynomial in \({ \mathbf{F} }[x]\), \(a\in { \mathbf{F} }\) by assumption, and fields are closed under taking powers and products.
Fall 2019 #4
Let \(F\) be a finite field with \(q\) elements. Let \(n\) be a positive integer relatively prime to \(q\) and let \(\omega\) be a primitive \(n\)th root of unity in an extension field of \(F\). Let \(E = F [\omega]\) and let \(k = [E : F]\).
-
Prove that \(n\) divides \(q^{k}-1\).
-
Let \(m\) be the order of \(q\) in \({\mathbf{Z}}/n{\mathbf{Z}}^{\times}\). Prove that \(m\) divides \(k\).
- Prove that \(m = k\).
\todo[inline]{Revisit, tricky!}
- \({ \mathbf{F} }^{\times}\) is always cyclic for \({ \mathbf{F} }\) a field.
- Lagrange: \(H\leq G \implies {\sharp}H \divides {\sharp}G\).
-
Since \({\left\lvert {F} \right\rvert} = q\) and \([E:F] = k\), we have \({\left\lvert {E} \right\rvert} = q^k\) and \({\left\lvert {E^{\times}} \right\rvert} = q^k-1\).
-
Noting that \(\zeta \in E^{\times}\) we must have \(n = o(\zeta) \divides {\left\lvert {E^{\times}} \right\rvert} = q^k-1\) by Lagrange’s theorem.
- Rephrasing (a), we have \begin{align*} n \divides q^k-1 &\iff q^k-1 \cong 0 \operatorname{mod}n \\ &\iff q^k \cong 1 \operatorname{mod}n \\ &\iff m \coloneqq o(q) \divides k .\end{align*}
-
Since \(m\divides k \iff k = \ell m\), (claim) there is an intermediate subfield \(M\) such that \begin{align*} E \leq M \leq F \quad k = [F:E] = [F:M] [M:E] = \ell m ,\end{align*}
so \(M\) is a degree \(m\) extension of \(E\).
-
Now consider \(M^{\times}\).
-
By the argument in (a), \(n\) divides \(q^m - 1 = {\left\lvert {M^{\times}} \right\rvert}\), and \(M^{\times}\) is cyclic, so it contains a cyclic subgroup \(H\) of order \(n\).
-
But then \(x\in H \implies p(x)\coloneqq x^n-1 = 0\), and since \(p(x)\) has at most \(n\) roots in a field.
-
So \(H = \left\{{x \in M {~\mathrel{\Big\vert}~}x^n-1 = 0}\right\}\), i.e. \(H\) contains all solutions to \(x^n-1\) in \(E[x]\).
-
But \(\zeta\) is one such solution, so \(\zeta \in H \subset M^{\times}\subset M\).
-
Since \(F[\zeta]\) is the smallest field extension containing \(\zeta\), we must have \(F = M\), so \(\ell = 1\), and \(k = m\).
Spring 2019 #2
Let \(F = { \mathbf{F} }_p\) , where \(p\) is a prime number.
-
Show that if \(\pi(x) \in F[x]\) is irreducible of degree \(d\), then \(\pi(x)\) divides \(x^{p^d} - x\).
-
Show that if \(\pi(x) \in F[x]\) is an irreducible polynomial that divides \(x^{p^n} - x\), then \(\deg \pi(x)\) divides \(n\).
-
Go to a field extension.
- Orders of multiplicative groups for finite fields are known.
- \({\mathbf{GF}}(p^n)\) is the splitting field of \(x^{p^n} - x \in { \mathbf{F} }_p[x]\).
- \(x^{p^d} - x \divides x^{p^n} - x \iff d \divides n\)
- \({\mathbf{GF}}(p^d) \leq {\mathbf{GF}}(p^n) \iff d\divides n\)
- \(x^{p^n} - x = \prod f_i(x)\) over all irreducible monic \(f_i\) of degree \(d\) dividing \(n\).
We can consider the quotient \(K = \displaystyle{\frac{{ \mathbf{F} }_p[x]}{\left\langle{\pi(x)}\right\rangle}}\), which since \(\pi(x)\) is irreducible is an extension of \({ \mathbf{F} }_p\) of degree \(d\) and thus a field of size \(p^d\) with a natural quotient map of rings \(\rho: { \mathbf{F} }_p[x] \to K\).
Since \(K^{\times}\) is a group of size \(p^d-1\), we know that for any \(y \in K^{\times}\), we have by Lagrange’s theorem that the order of \(y\) divides \(p^d-1\) and so \(y^{p^d} = y\).
So every element in \(K\) is a root of \(q(x) = x^{p^d}-x\).
Since \(\rho\) is a ring morphism, we have
\begin{align*} \rho(q(x)) = \rho(x^{p^d} - x) &= \rho(x)^{p^d} - \rho(x) = 0 \in K \\ &\iff q(x) \in \ker \rho \\ &\iff q(x) \in \left\langle{\pi(x)}\right\rangle \\ &\iff \pi(x) \divides q(x) = x^{p^d}-x ,\end{align*} where we’ve used that “to contain is to divide” in the last step.
\(\pi(x)\) divides \(x^{p^n}-x \iff \deg \pi\) divides \(n\).
Let \(L \cong {\mathbf{GF}}(p^n)\) be the splitting field of \(\phi_n(x) \coloneqq x^{p^n}-x\); then since \(\pi \divides \phi_n\) by assumption, \(\pi\) splits in \(L\). Let \(\alpha \in L\) be any root of \(\pi\); then there is a tower of extensions \({ \mathbf{F} }_p \leq { \mathbf{F} }_p(\alpha) \leq L\).
Then \({ \mathbf{F} }_p \leq { \mathbf{F} }_p(\alpha) \leq L\), and so \begin{align*} n &= [L: { \mathbf{F} }_p] \\ &= [L: { \mathbf{F} }_p(\alpha)]~[{ \mathbf{F} }_p(\alpha): { \mathbf{F} }_p] \\ &= \ell d ,\end{align*}
for some \(\ell \in {\mathbf{Z}}^{\geq 1}\), so \(d\) divides \(n\).
\(\impliedby\): If \(d\divides n\), use the fact (claim) that \(x^{p^n} - x = \prod f_i(x)\) over all irreducible monic \(f_i\) of degree \(d\) dividing \(n\). So \(f = f_i\) for some \(i\).
\(\star\) Fall 2016 #5
How many monic irreducible polynomials over \({ \mathbf{F} }_p\) of prime degree \(\ell\) are there? Justify your answer.
\(\star\) Fall 2013 #7
Let \(F = { \mathbf{F} }_2\) and let \(\mkern 1.5mu\overline{\mkern-1.5muF\mkern-1.5mu}\mkern 1.5mu\) denote its algebraic closure.
-
Show that \(\mkern 1.5mu\overline{\mkern-1.5muF\mkern-1.5mu}\mkern 1.5mu\) is not a finite extension of \(F\).
-
Suppose that \(\alpha \in \mkern 1.5mu\overline{\mkern-1.5muF\mkern-1.5mu}\mkern 1.5mu\) satisfies \(\alpha^{17} = 1\) and \(\alpha\neq 1\). Show that \(F(\alpha)/F\) has degree 8.
General Field Extensions
Spring 2020 #3
Let \(E\) be an extension field of \(F\) and \(\alpha\in E\) be algebraic of odd degree over \(F\).
-
Show that \(F(\alpha) = F(\alpha^2)\).
-
Prove that \(\alpha^{2020}\) is algebraic of odd degree over \(F\).
Spring 2012 #1
Suppose that \(F\subset E\) are fields such that \(E/F\) is Galois and \({\left\lvert {{ \operatorname{Gal}}(E/F)} \right\rvert} = 14\).
-
Show that there exists a unique intermediate field \(K\) with \(F\subset K \subset E\) such that \([K: F] = 2\).
-
Assume that there are at least two distinct intermediate subfields \(F \subset L_1, L_2 \subset E\) with \([L_i: F]= 7\). Prove that \({ \operatorname{Gal}}(E/F)\) is nonabelian.
Spring 2019 #8
Let \(\zeta = e^{2\pi i/8}\).
-
What is the degree of \({\mathbf{Q}}(\zeta)/{\mathbf{Q}}\)?
-
How many quadratic subfields of \({\mathbf{Q}}(\zeta)\) are there?
- What is the degree of \({\mathbf{Q}}(\zeta, \sqrt[4] 2)\) over \({\mathbf{Q}}\)?
-
\(\zeta_n \coloneqq e^{2\pi i \over n}\), and \(\zeta_n^k\) is a primitive \(n\)th root of unity \(\iff \gcd(n, k) = 1\)
- In general, \(\zeta_n^k\) is a primitive \({n \over \gcd(n, k)}\)th root of unity.
- \(\deg \Phi_n(x) = \phi(n)\)
-
\(\phi(p^k) = p^k - p^{k-1} = p^{k-1}(p-1)\)
- Proof: for a nontrivial gcd, the possibilities are \begin{align*} p, 2p, 3p, 4p, \cdots, p^{k-2}p, p^{k-1}p .\end{align*}
- \({ \mathsf{Gal}}({\mathbf{Q}}(\zeta)/{\mathbf{Q}}) \cong {\mathbf{Z}}/(n)^{\times}\)
Let \(K = {\mathbf{Q}}(\zeta)\).
- \(\zeta \coloneqq e^{2\pi i / 8}\) is a primitive \(8\)th root of unity
- The minimal polynomial of an \(n\)th root of unity is the \(n\)th cyclotomic polynomial \(\Phi_n\)
- The degree of the field extension is the degree of \(\Phi_8\), which is \begin{align*} \phi(8) = \phi(2^3) = 2^{3-1} \cdot (2-1) = 4 .\end{align*}
- So \([{\mathbf{Q}}(\zeta): {\mathbf{Q}}] = 4\).
- \({ \mathsf{Gal}}({\mathbf{Q}}(\zeta)/{\mathbf{Q}}) \cong {\mathbf{Z}}/(8)^{\times}\cong {\mathbf{Z}}/(4)\) by general theory
- \({\mathbf{Z}}/(4)\) has exactly one subgroup of index 2.
- Thus there is exactly one intermediate field of degree 2 (a quadratic extension).
-
Let \(L = {\mathbf{Q}}(\zeta, \sqrt[4] 2)\).
-
Note \({\mathbf{Q}}(\zeta) = {\mathbf{Q}}(i, \sqrt 2)\)
-
\({\mathbf{Q}}(i, \sqrt{2})\subseteq {\mathbf{Q}}(\zeta)\)
- \(\zeta_8^2 = i\), and \(\zeta_8 = \sqrt{2}^{-1}+ i\sqrt{2}^{-1}\) so \(\zeta_8 + \zeta_8 ^{-1}= 2/\sqrt{2} = \sqrt{2}\).
-
\({\mathbf{Q}}(\zeta) \subseteq {\mathbf{Q}}(i, \sqrt{2})\):
- \(\zeta = e^{2\pi i / 8} = \sin(\pi/4) + i\cos(\pi/4) = {\sqrt 2 \over 2}\qty{1+i}\).
-
\({\mathbf{Q}}(i, \sqrt{2})\subseteq {\mathbf{Q}}(\zeta)\)
-
Thus \(L = {\mathbf{Q}}(i, \sqrt{2})(\sqrt[4]{2}) = {\mathbf{Q}}(i, \sqrt 2, \sqrt[4] 2) = {\mathbf{Q}}(i, \sqrt[4]{2})\).
- Uses the fact that \({\mathbf{Q}}(\sqrt 2) \subseteq {\mathbf{Q}}(\sqrt[4] 2)\) since \(\sqrt[4]{2}^2 = \sqrt{2}\)
-
Conclude \begin{align*} [L: {\mathbf{Q}}] = [L: {\mathbf{Q}}(\sqrt[4] 2)] ~[{\mathbf{Q}}(\sqrt[4] 2): {\mathbf{Q}}] = 2 \cdot 4 = 8 \end{align*} using the fact that the minimal polynomial of \(i\) over any subfield of \({\mathbf{R}}\) is always \(x^2 + 1\), so \(\min_{{\mathbf{Q}}(\sqrt[4] 2)}(i) = x^2 + 1\) which is degree 2.
Fall 2017 #3
Let \(F\) be a field. Let \(f(x)\) be an irreducible polynomial in \(F[x]\) of degree \(n\) and let \(g(x)\) be any polynomial in \(F[x]\). Let \(p(x)\) be an irreducible factor (of degree \(m\)) of the polynomial \(f(g(x))\).
Prove that \(n\) divides \(m\). Use this to prove that if \(r\) is an integer which is not a perfect square, and \(n\) is a positive integer then every irreducible factor of \(x^{2n} - r\) over \({\mathbf{Q}}[x]\) has even degree.
Spring 2015 #2
Let \({ \mathbf{F} }\) be a finite field.
-
Give (with proof) the decomposition of the additive group \(({ \mathbf{F} }, +)\) into a direct sum of cyclic groups.
-
The exponent of a finite group is the least common multiple of the orders of its elements. Prove that a finite abelian group has an element of order equal to its exponent.
- Prove that the multiplicative group \(({ \mathbf{F} }^{\times}, \cdot)\) is cyclic.
Spring 2014 #3
Let \(F\subset C\) be a field extension with \(C\) algebraically closed.
-
Prove that the intermediate field \(C_{\text{alg}} \subset C\) consisting of elements algebraic over \(F\) is algebraically closed.
-
Prove that if \(F\to E\) is an algebraic extension, there exists a homomorphism \(E\to C\) that is the identity on \(F\).
Modules
Annihilators
Fall 2021 #6
Let \(R\) be a commutative ring with unit and let \(M\) be an \(R\)-module. Define the annihilator of \(M\) to be \begin{align*} \operatorname{Ann}(M):=\{r \in R \mathrel{\Big|}r \cdot m=0 \text { for all } m \in M\} \end{align*}
-
Prove that \(\operatorname{Ann}(M)\) is an ideal in \(R\).
-
Conversely, prove that every ideal in \(R\) is the annihilator of some \(R\)-module.
- Give an example of a module \(M\) over a ring \(R\) such that each element \(m \in M\) has a nontrivial annihilator \(\operatorname{Ann}(m):=\{r \in R \mathrel{\Big|}r \cdot m=0\}\), but \(\operatorname{Ann}(M)=\{0\}\)
Spring 2017 #5
Let \(R\) be an integral domain and let \(M\) be a nonzero torsion \(R{\hbox{-}}\)module.
-
Prove that if \(M\) is finitely generated then the annihilator in \(R\) of \(M\) is nonzero.
-
Give an example of a non-finitely generated torsion \(R{\hbox{-}}\)module whose annihilator is \((0)\), and justify your answer.
Torsion and the Structure Theorem
\(\star\) Fall 2019 #5
Let \(R\) be a ring and \(M\) an \(R{\hbox{-}}\)module.
Recall that the set of torsion elements in M is defined by \begin{align*} \operatorname{Tor}(M) = \{m \in M {~\mathrel{\Big\vert}~}\exists r \in R, ~r \neq 0, ~rm = 0\} .\end{align*}
-
Prove that if \(R\) is an integral domain, then \(\operatorname{Tor}(M )\) is a submodule of \(M\) .
-
Give an example where \(\operatorname{Tor}(M )\) is not a submodule of \(M\).
- If \(R\) has zero-divisors, prove that every non-zero \(R{\hbox{-}}\)module has non-zero torsion elements.
- One-step submodule test.
It suffices to show that \begin{align*} r\in R, ~t_1, t_2\in \operatorname{Tor}(M) \implies rt_1 + t_2 \in \operatorname{Tor}(M) .\end{align*}
We have \begin{align*} t_1 \in \operatorname{Tor}(M) &\implies \exists s_1 \neq 0 \text{ such that } s_1 t_1 = 0 \\ t_2 \in \operatorname{Tor}(M) &\implies \exists s_2 \neq 0 \text{ such that } s_2 t_2 = 0 .\end{align*}
Since \(R\) is an integral domain, \(s_1 s_2 \neq 0\). Then \begin{align*} s_1 s_2(rt_1 + t_2) &= s_1 s_2 r t_1 + s_1 s_2t_2 \\ &= s_2 r (s_1 t_1) + s_1 (s_2 t_2) \quad\text{since $R$ is commutative} \\ &= s_2 r(0) + s_1(0) \\ &= 0 .\end{align*}
Let \(R = {\mathbf{Z}}/6{\mathbf{Z}}\) as a \({\mathbf{Z}}/6{\mathbf{Z}}{\hbox{-}}\)module, which is not an integral domain as a ring.
Then \([3]_6\curvearrowright[2]_6 = [0]_6\) and \([2]_6\curvearrowright[3]_6 = [0]_6\), but \([2]_6 + [3]_6 = [5]_6\), where 5 is coprime to 6, and thus \([n]_6\curvearrowright[5]_6 = [0] \implies [n]_6 = [0]_6\). So \([5]_6\) is not a torsion element.
So the set of torsion elements are not closed under addition, and thus not a submodule.
Suppose \(R\) has zero divisors \(a,b \neq 0\) where \(ab = 0\). Then for any \(m\in M\), we have \(b\curvearrowright m \coloneqq bm \in M\) as well, but then \begin{align*} a\curvearrowright bm = (ab)\curvearrowright m = 0\curvearrowright m = 0_M ,\end{align*} so \(m\) is a torsion element for any \(m\).
\(\star\) Spring 2019 #5
Let \(R\) be an integral domain. Recall that if \(M\) is an \(R{\hbox{-}}\)module, the rank of \(M\) is defined to be the maximum number of \(R{\hbox{-}}\)linearly independent elements of \(M\) .
-
Prove that for any \(R{\hbox{-}}\)module \(M\), the rank of \(\operatorname{Tor}(M )\) is 0.
-
Prove that the rank of \(M\) is equal to the rank of of \(M/\operatorname{Tor}(M )\).
- Suppose that M is a non-principal ideal of \(R\).
Prove that \(M\) is torsion-free of rank 1 but not free.
- Todo
- Suppose toward a contradiction \(\operatorname{Tor}(M)\) has rank \(n \geq 1\).
- Then \(\operatorname{Tor}(M)\) has a linearly independent generating set \(B = \left\{{\mathbf{r}_1, \cdots, \mathbf{r}_n}\right\}\), so in particular \begin{align*} \sum_{i=1}^n s_i \mathbf{r}_i = 0 \implies s_i = 0_R \,\forall i .\end{align*}
- Let \(\mathbf{r}\) be any of of these generating elements.
- Since \(\mathbf{r}\in \operatorname{Tor}(M)\), there exists an \(s\in R\setminus 0_R\) such that \(s\mathbf{r} = 0_M\).
- Then \(s\mathbf{r} = 0\) with \(s\neq 0\), so \(\left\{{\mathbf{r}}\right\} \subseteq B\) is not a linearly independent set, a contradiction.
- Let \(n = \operatorname{rank}M\), and let \(\mathcal B = \left\{{\mathbf{r}_i}\right\}_{i=1}^n \subseteq R\) be a generating set.
- Let \(\tilde M \coloneqq M/\operatorname{Tor}(M)\) and \(\pi: M \to M'\) be the canonical quotient map.
\begin{align*} \tilde {\mathcal{B}}\coloneqq\pi(\mathcal B) = \left\{{\mathbf{r}_i + \operatorname{Tor}(M)}\right\} \end{align*} is a basis for \(\tilde M\).
Note that the proof follows immediately.
-
Suppose that \begin{align*} \sum_{i=1}^n s_i (\mathbf{r}_i + \operatorname{Tor}(M)) = \mathbf{0}_{\tilde M} .\end{align*}
-
Then using the definition of coset addition/multiplication, we can write this as \begin{align*} \sum_{i=1}^n \qty { s_i \mathbf{r}_i + \operatorname{Tor}(M)} = \qty{ \sum_{i=1}^n s_i \mathbf{r}_i} + \operatorname{Tor}(M) = 0_{\tilde M} .\end{align*}
-
Since \(\tilde{\mathbf{x}} = 0 \in \tilde M \iff \tilde{\mathbf{x}} = \mathbf{x} + \operatorname{Tor}(M)\) where \(\mathbf{x} \in \operatorname{Tor}(M)\), this forces \(\sum s_i \mathbf{r}_i \in \operatorname{Tor}(M)\).
-
Then there exists a scalar \(\alpha\in R^{\bullet}\) such that \(\alpha \sum s_i \mathbf{r}_i = 0_M\).
-
Since \(R\) is an integral domain and \(\alpha \neq 0\), we must have \(\sum s_i \mathbf{r}_i = 0_M\).
-
Since \(\left\{{\mathbf{r}_i}\right\}\) was linearly independent in \(M\), we must have \(s_i = 0_R\) for all \(i\).
-
Write \(\pi(\mathcal B) = \left\{{\mathbf{r}_i + \operatorname{Tor}(M)}\right\}_{i=1}^n\) as a set of cosets.
-
Letting \(\mathbf{x} \in M'\) be arbitrary, we can write \(\mathbf{x} = \mathbf{m} + \operatorname{Tor}(M)\) for some \(\mathbf{m} \in M\) where \(\pi(\mathbf{m}) = \mathbf{x}\) by surjectivity of \(\pi\).
-
Since \(\mathcal B\) is a basis for \(M\), we have \(\mathbf{m} = \sum_{i=1}^n s_i \mathbf{r}_i\), and so \begin{align*} \mathbf{x} &= \pi(\mathbf{m}) \\ &\coloneqq\pi\qty{ \sum_{i=1}^n s_i \mathbf{r}_i} \\ &= \sum_{i=1}^n s_i \pi(\mathbf{r}_i) \quad\text{since $\pi$ is an $R{\hbox{-}}$module morphism}\\ &\coloneqq\sum_{i=1}^n s_i \mathbf{(}\mathbf{r}_i + \operatorname{Tor}(M)) ,\end{align*} which expresses \(\mathbf{x}\) as a linear combination of elements in \(\mathcal B'\).
Notation: Let \(0_R\) denote \(0\in R\) regarded as a ring element, and \(\mathbf{0} \in R\) denoted \(0_R\) regarded as a module element (where \(R\) is regarded as an \(R{\hbox{-}}\)module over itself)
-
Claim: If \(I\subseteq R\) is an ideal and a free \(R{\hbox{-}}\)module, then \(I\) is principal .
-
Suppose \(I\) is free and let \(I = \left\langle{B}\right\rangle\) for some basis, we will show \({\left\lvert {B} \right\rvert} = 1\)>
-
Toward a contradiction, suppose \({\left\lvert {B} \right\rvert} \geq 2\) and let \(m_1, m_2\in B\).
-
Then since \(R\) is commutative, \(m_2 m_1 - m_1 m_2 = 0\) and this yields a linear dependence
-
So \(B\) has only one element \(m\).
-
But then \(I = \left\langle{m}\right\rangle = R_m\) is cyclic as an \(R{\hbox{-}}\) module and thus principal as an ideal of \(R\).
-
Now since \(M\) was assumed to not be principal, \(M\) is not free (using the contrapositive of the claim).
-
-
For any module, we can take an element \(\mathbf{m}\in M^{\bullet}\) and consider the cyclic submodule \(R\mathbf{m}\).
-
Since \(M\) is not principle, it is not the zero ideal, and contains at least two elements. So we can consider an element \(\mathbf{m}\in M\).
-
We have \(\operatorname{rank}_R(M) \geq 1\), since \(R\mathbf{m} \leq M\) and \(\left\{{m}\right\}\) is a subset of some spanning set.
-
\(R\mathbf{m}\) can not be linearly dependent, since \(R\) is an integral domain and \(M\subseteq R\), so \(\alpha \mathbf{m} = \mathbf{0} \implies \alpha = 0_R\).
-
Claim: since \(R\) is commutative, \(\operatorname{rank}_R(M) \leq 1\).
- If we take two elements \(\mathbf{m}, \mathbf{n} \in M^{\bullet}\), then since \(m, n\in R\) as well, we have \(nm = mn\) and so \begin{align*} (n)\mathbf{m} + (-m)\mathbf{n} = 0_R = \mathbf{0} \end{align*} is a linear dependence.
\(M\) is torsion-free:
-
Let \(\mathbf{x} \in \operatorname{Tor}M\), then there exists some \(r\neq 0\in R\) such that \(r\mathbf{x} = \mathbf{0}\).
-
But \(\mathbf{x}\in R\) as well and \(R\) is an integral domain, so \(\mathbf{x}=0_R\), and thus \(\operatorname{Tor}(M) = \left\{{0_R}\right\}\).
\(\star\) Spring 2020 #6
Let \(R\) be a ring with unity.
-
Give a definition for a free module over \(R\).
-
Define what it means for an \(R{\hbox{-}}\)module to be torsion free.
-
Prove that if \(F\) is a free module, then any short exact sequence of \(R{\hbox{-}}\)modules of the following form splits: \begin{align*} 0 \to N \to M \to F \to 0 .\end{align*}
-
Let \(R\) be a PID. Show that any finitely generated \(R{\hbox{-}}\)module \(M\) can be expressed as a direct sum of a torsion module and a free module.
You may assume that a finitely generated torsionfree module over a PID is free.
Let \(R\) be a ring with 1.
An \(R{\hbox{-}}\)module \(M\) is free if any of the following conditions hold:
- \(M\) admits an \(R{\hbox{-}}\)linearly independent spanning set \(\left\{{\mathbf{b}_\alpha}\right\}\), so \begin{align*}m\in M \implies m = \sum_\alpha r_\alpha \mathbf{b}_\alpha\end{align*} and \begin{align*}\sum_\alpha r_\alpha \mathbf{b}_\alpha = 0_M \implies r_\alpha = 0_R\end{align*} for all \(\alpha\).
- \(M\) admits a decomposition \(M \cong \bigoplus_{\alpha} R\) as a direct sum of \(R{\hbox{-}}\)submodules.
- There is a nonempty set \(X\) an monomorphism \(X\hookrightarrow M\) of sets such that for every \(R{\hbox{-}}\)module \(N\), every set map \(X\to N\) lifts to a unique \(R{\hbox{-}}\)module morphism \(M\to N\), so the following diagram commutes:
Equivalently, \begin{align*} \mathop{\mathrm{Hom}}_{\mathsf{Set}}(X, \mathop{\mathrm{Forget}}(N)) \xrightarrow{\sim} \mathop{\mathrm{Hom}}_{ {}_{R}{\mathsf{Mod}}}(M, N) .\end{align*}
-
Define the annihilator:
\begin{align*}
\operatorname{Ann}(m) \coloneqq\left\{{r\in R {~\mathrel{\Big\vert}~}r\cdot m = 0_M}\right\} {~\trianglelefteq~}R
.\end{align*}
- Note that \(mR \cong R/\operatorname{Ann}(m)\).
- Define the torsion submodule: \begin{align*} M_t \coloneqq\left\{{m\in M {~\mathrel{\Big\vert}~}\operatorname{Ann}(m) \neq 0}\right\} \leq M \end{align*}
- \(M\) is torsionfree iff \(M_t = 0\) is the trivial submodule.
-
Let the following be an SES where \(F\) is a free \(R{\hbox{-}}\)module: \begin{align*} 0 \to N \to M \xrightarrow{\pi} F \to 0 .\end{align*}
-
Since \(F\) is free, there is a generating set \(X = \left\{{x_\alpha}\right\}\) and a map \(\iota:X\hookrightarrow F\) satisfying the 3rd property from (a).
- If we construct any map \(f: X\to M\), the universal property modules will give a lift \(\tilde f: F\to M\)
-
Identify \(X\) with \(\iota(X) \subseteq F\).
-
For every \(x\in X\), the preimage \(\pi^{-1}(x)\) is nonempty by surjectivity. So arbitrarily pick any preimage.
-
\(\left\{{\iota(x_\alpha)}\right\} \subseteq F\) and \(\pi\) is surjective, so choose fibers \(\left\{{y_\alpha}\right\} \subseteq M\) such that \(\pi(y_\alpha) = \iota(x_\alpha)\) and define \begin{align*} f: X&\to M \\ x_\alpha &\mapsto y_\alpha .\end{align*}
-
The universal property yields \(h: F\to M\):
-
It remains to check that it’s a section.
- Write \(f= \sum r_i x_i\), then since both maps are \(R{\hbox{-}}\)module morphism, by \(R{\hbox{-}}\)linearity we can write \begin{align*} (\pi \circ h)(f) &= (\pi \circ h)\qty{ \sum r_i x_i } \\ &= \sum r_i (\pi \circ h)(x_i) ,\end{align*} but since \(h(x_i) \in \pi^{-1}(x_i)\), we have \((\pi \circ h)(x_i) = x_i\). So this recovers \(f\).
-
Free implies projective
- Universal property of projective objects: for every epimorphism \(\pi:M\twoheadrightarrow N\) and every \(f:P\to N\) there exists a unique lift \(\tilde f: P\to M\):
- Construct \(\phi\) in the following diagram using the same method as above (surjectivity to pick elements in preimage):
- Now take the identity map, then commutativity is equivalent to being a section.
There is a SES
\(M/M_t\) is a free \(R{\hbox{-}}\)module, so this sequence splits and \(M\cong M_t \oplus {M\over M_t}\), where \(M_t\) is a torsion \(R{\hbox{-}}\)module.
Note that by the hint, since \(R\) is a PID, it suffices to show that \(M/M_t\) is torsionfree.
- Let \(m+M_t \in M/M_t\) be arbitrary. Suppose this is a torsion element, the claim is that it must be the trivial coset. This will follow if \(m\in M_t\)
- Since this is torsion, there exists \(r\in R\) such that \begin{align*} M_t = r(m + M_t) \coloneqq(rm) + M_t \implies rm\in M_t .\end{align*}
- Then \(rm\) is torsion in \(M\), so there exists some \(s\in R\) such \(s(rm) = 0_M\).
- Then \((sr)m = 0_M\) which forces \(m\in M_t\)
Spring 2012 #5
Let \(M\) be a finitely generated module over a PID \(R\).
-
\(M_t\) be the set of torsion elements of \(M\), and show that \(M_t\) is a submodule of \(M\).
-
Show that \(M/M_t\) is torsion free.
- Prove that \(M \cong M_t \oplus F\) where \(F\) is a free module.
Fall 2019 Final #3
Let \(R = k[x]\) for \(k\) a field and let \(M\) be the \(R{\hbox{-}}\)module given by \begin{align*} M=\frac{k[x]}{(x-1)^{3}} \oplus \frac{k[x]}{\left(x^{2}+1\right)^{2}} \oplus \frac{k[x]}{(x-1)\left(x^{2}+1\right)^{4}} \oplus \frac{k[x]}{(x+2)\left(x^{2}+1\right)^{2}} .\end{align*} Describe the elementary divisors and invariant factors of \(M\).
Fall 2019 Final #4
Let \(I = (2, x)\) be an ideal in \(R = {\mathbf{Z}}[x]\), and show that \(I\) is not a direct sum of nontrivial cyclic \(R{\hbox{-}}\)modules.
Fall 2019 Final #5
Let \(R\) be a PID.
-
Classify irreducible \(R{\hbox{-}}\)modules up to isomorphism.
-
Classify indecomposable \(R{\hbox{-}}\)modules up to isomorphism.
Fall 2019 Final #6
Let \(V\) be a finite-dimensional \(k{\hbox{-}}\)vector space and \(T:V\to V\) a non-invertible \(k{\hbox{-}}\)linear map. Show that there exists a \(k{\hbox{-}}\)linear map \(S:V\to V\) with \(T\circ S = 0\) but \(S\circ T\neq 0\).
Fall 2019 Final #7
Let \(A\in M_n({\mathbf{C}})\) with \(A^2 = A\). Show that \(A\) is similar to a diagonal matrix, and exhibit an explicit diagonal matrix similar to \(A\).
Fall 2019 Final #10
Show that the eigenvalues of a Hermitian matrix \(A\) are real and that \(A = PDP^{-1}\) where \(P\) is an invertible matrix with orthogonal columns.
Fall 2020 #7
Let \(A \in \operatorname{Mat}(n\times n, {\mathbf{R}})\) be arbitrary. Make \({\mathbf{R}}^n\) into an \({\mathbf{R}}[x]{\hbox{-}}\)module by letting \(f(x).\mathbf{v} \coloneqq f(A)(\mathbf{v})\) for \(f(\mathbf{v})\in {\mathbf{R}}[x]\) and \(\mathbf{v} \in {\mathbf{R}}^n\). Suppose that this induces the following direct sum decomposition: \begin{align*} {\mathbf{R}}^n \cong { {\mathbf{R}}[x] \over \left\langle{ (x-1)^3 }\right\rangle } \oplus { {\mathbf{R}}[x] \over \left\langle{ (x^2+1)^2 }\right\rangle } \oplus { {\mathbf{R}}[x] \over \left\langle{ (x-1)(x^2-1)(x^2+1)^4 }\right\rangle } \oplus { {\mathbf{R}}[x] \over \left\langle{ (x+2)(x^2+1)^2 }\right\rangle } .\end{align*}
-
Determine the elementary divisors and invariant factors of \(A\).
-
Determine the minimal polynomial of \(A\).
- Determine the characteristic polynomial of \(A\).
Misc/Unsorted
Spring 2017 #3
Let \(R\) be a commutative ring with 1. Suppose that \(M\) is a free \(R{\hbox{-}}\)module with a finite basis \(X\).
-
Let \(I {~\trianglelefteq~}R\) be a proper ideal. Prove that \(M/IM\) is a free \(R/I{\hbox{-}}\)module with basis \(X'\), where \(X'\) is the image of \(X\) under the canonical map \(M\to M/IM\).
-
Prove that any two bases of \(M\) have the same number of elements. You may assume that the result is true when \(R\) is a field.
Spring 2020 #5
Let \(R\) be a ring and \(f: M\to N\) and \(g: N\to M\) be \(R{\hbox{-}}\)module homomorphisms such that \(g\circ f = \operatorname{id}_M\). Show that \(N \cong \operatorname{im}f \oplus \ker g\).
- We have the following situation:
-
Claim: \(\operatorname{im}f + \ker g \subseteq N\), and this is in fact an equality.
- For \(n\in N\), write \begin{align*} n = n + (f\circ g)(n) - (f\circ g)(n) = \qty{n - (f\circ g)(n) } + (f\circ g)(n) .\end{align*}
- The first term is in \(\ker g\): \begin{align*} g \qty{ n - (f\circ g)(n) } &= g(n) - (g\circ f \circ g)(n)\\ &= g(n) - (\operatorname{id}_N \circ g)(n)\\ &= g(n) - g(n) \\ &= 0 .\end{align*}
- The second term is clearly in \(\operatorname{im}f\).
-
Claim: the sum is direct.
- Suppose \(n\in \ker(g) \cap\operatorname{im}(f)\), so \(g(n) = 0\) and \(n=f(m)\) for some \(m\in M\). Then \begin{align*} 0 = g(n) = g(f(m)) = (g\circ f)(m) = \operatorname{id}_M(m) = m ,\end{align*} so \(m=0\) and since \(f\) is a morphism in \(R{\hbox{-}}\)modules, \(n\coloneqq f(m) = 0\).
Fall 2018 #6
Let \(R\) be a commutative ring, and let \(M\) be an \(R{\hbox{-}}\)module. An \(R{\hbox{-}}\)submodule \(N\) of \(M\) is maximal if there is no \(R{\hbox{-}}\)module \(P\) with \(N \subsetneq P \subsetneq M\).
-
Show that an \(R{\hbox{-}}\)submodule \(N\) of \(M\) is maximal \(\iff M /N\) is a simple \(R{\hbox{-}}\)module: i.e., \(M /N\) is nonzero and has no proper, nonzero \(R{\hbox{-}}\)submodules.
-
Let \(M\) be a \({\mathbf{Z}}{\hbox{-}}\)module. Show that a \({\mathbf{Z}}{\hbox{-}}\)submodule \(N\) of \(M\) is maximal \(\iff {\sharp}M /N\) is a prime number.
- Let \(M\) be the \({\mathbf{Z}}{\hbox{-}}\)module of all roots of unity in \({\mathbf{C}}\) under multiplication. Show that there is no maximal \({\mathbf{Z}}{\hbox{-}}\)submodule of \(M\).
- Todo
By the correspondence theorem, submodules of \(M/N\) biject with submodules \(A\) of \(M\) containing \(N\).
So
-
\(M\) is maximal:
-
\(\iff\) no such (proper, nontrivial) submodule \(A\) exists
-
\(\iff\) there are no (proper, nontrivial) submodules of \(M/N\)
-
\(\iff M/N\) is simple.
Identify \({\mathbf{Z}}{\hbox{-}}\)modules with abelian groups, then by (a), \(N\) is maximal \(\iff\) \(M/N\) is simple \(\iff\) \(M/N\) has no nontrivial proper subgroups.\
By Cauchy’s theorem, if \({\left\lvert {M/N} \right\rvert} = ab\) is a composite number, then \(a\divides ab \implies\) there is an element (and thus a subgroup) of order \(a\). In this case, \(M/N\) contains a nontrivial proper cyclic subgroup, so \(M/N\) is not simple. So \({\left\lvert {M/N} \right\rvert}\) can not be composite, and therefore must be prime.
-
Let \(G = \left\{{x \in {\mathbf{C}}{~\mathrel{\Big\vert}~}x^n=1 \text{ for some }n\in {\mathbb{N}}}\right\}\), and suppose \(H < G\) is a proper submodule.
-
Since \(H\neq G\), there is some \(p\) and some \(k\) such that \(\zeta_{p^k}\not\in H\).
- Otherwise, if \(H\) contains every \(\zeta_{p^k}\) it contains every \(\zeta_n\)
Then there must be a prime \(p\) such that the \(\zeta_{p^k} \not \in H\) for all \(k\) greater than some constant \(m\) – otherwise, we can use the fact that if \(\zeta_{p^k} \in H\) then \(\zeta_{p^\ell} \in H\) for all \(\ell \leq k\), and if \(\zeta_{p^k} \in H\) for all \(p\) and all \(k\) then \(H = G\).
But this means there are infinitely many elements in \(G\setminus H\), and so \(\infty = [G: H] = {\left\lvert {G/H} \right\rvert}\) is not a prime. Thus by (b), \(H\) can not be maximal, a contradiction.
Fall 2019 Final #2
Consider the \({\mathbf{Z}}{\hbox{-}}\)submodule \(N\) of \({\mathbf{Z}}^3\) spanned by \begin{align*} f_1 &= [-1, 0, 1], \\ f_2 &= [2,-3,1], \\ f_3 &= [0, 3, 1], \\ f_4 &= [3,1,5] .\end{align*} Find a basis for \(N\) and describe \({\mathbf{Z}}^3/N\).
Spring 2018 #6
Let \begin{align*} M &= \{(w, x, y, z) \in {\mathbf{Z}}^4 {~\mathrel{\Big\vert}~}w + x + y + z \in 2{\mathbf{Z}}\} \\ N &= \left\{{ (w, x, y, z) \in {\mathbf{Z}}^4 {~\mathrel{\Big\vert}~}4\divides (w - x),~ 4\divides (x - y),~ 4\divides ( y - z) }\right\} .\end{align*}
-
Show that \(N\) is a \({\mathbf{Z}}{\hbox{-}}\)submodule of \(M\) .
-
Find vectors \(u_1 , u_2 , u_3 , u_4 \in {\mathbf{Z}}^4\) and integers \(d_1 , d_2 , d_3 , d_4\) such that \begin{align*} \{ u_1 , u_2 , u_3 , u_4 \} && \text{is a free basis for }M \\ \{ d_1 u_1,~ d_2 u_2,~ d_3 u_3,~ d_4 u_4 \} && \text{is a free basis for }N \end{align*}
- Use the previous part to describe \(M/N\) as a direct sum of cyclic \({\mathbf{Z}}{\hbox{-}}\)modules.
Spring 2018 #7
Let \(R\) be a PID and \(M\) be an \(R{\hbox{-}}\)module. Let \(p\) be a prime element of \(R\). The module \(M\) is called \(\left\langle{p}\right\rangle{\hbox{-}}\)primary if for every \(m \in M\) there exists \(k > 0\) such that \(p^k m = 0\).
-
Suppose M is \(\left\langle{p}\right\rangle{\hbox{-}}\)primary. Show that if \(m \in M\) and \(t \in R, ~t \not\in \left\langle{p}\right\rangle\), then there exists \(a \in R\) such that \(atm = m\).
-
A submodule \(S\) of \(M\) is said to be pure if \(S \cap r M = rS\) for all \(r \in R\). Show that if \(M\) is \(\left\langle{p}\right\rangle{\hbox{-}}\)primary, then \(S\) is pure if and only if \(S \cap p^k M = p^k S\) for all \(k \geq 0\).
Fall 2016 #6
Let \(R\) be a ring and \(f: M\to N\) and \(g: N\to M\) be \(R{\hbox{-}}\)module homomorphisms such that \(g\circ f = \operatorname{id}_M\). Show that \(N\cong \operatorname{im}f \oplus \ker g\).
Spring 2016 #4
Let \(R\) be a ring with the following commutative diagram of \(R{\hbox{-}}\)modules, where each row represents a short exact sequence of \(R{\hbox{-}}\)modules:
Prove that if \(\alpha\) and \(\gamma\) are isomorphisms then \(\beta\) is an isomorphism.
Spring 2015 #8
Let \(R\) be a PID and \(M\) a finitely generated \(R{\hbox{-}}\)module.
-
Prove that there are \(R{\hbox{-}}\)submodules \begin{align*} 0 = M_0 \subset M_1 \subset \cdots \subset M_n = M \end{align*} such that for all \(0\leq i \leq n-1\), the module \(M_{i+1}/M_i\) is cyclic.
-
Is the integer \(n\) in part (a) uniquely determined by \(M\)? Prove your answer.
Fall 2012 #6
Let \(R\) be a ring and \(M\) an \(R{\hbox{-}}\)module. Recall that \(M\) is Noetherian iff any strictly increasing chain of submodule \(M_1 \subsetneq M_2 \subsetneq \cdots\) is finite. Call a proper submodule \(M' \subsetneq M\) intersection-decomposable if it can not be written as the intersection of two proper submodules \(M' = M_1\cap M_2\) with \(M_i \subsetneq M\).
Prove that for every Noetherian module \(M\), any proper submodule \(N\subsetneq M\) can be written as a finite intersection \(N = N_1 \cap\cdots \cap N_k\) of intersection-indecomposable modules.
Fall 2019 Final #1
Let \(A\) be an abelian group, and show \(A\) is a \({\mathbf{Z}}{\hbox{-}}\)module in a unique way.
Fall 2020 #6
Let \(R\) be a ring with \(1\) and let \(M\) be a left \(R{\hbox{-}}\)module. If \(I\) is a left ideal of \(R\), define \begin{align*} IM \coloneqq\left\{{ \sum_{i=1}^{N < \infty} a_i m_i {~\mathrel{\Big\vert}~}a_i \in I, m_i \in M, n\in {\mathbb{N}}}\right\} ,\end{align*} i.e. the set of finite sums of of elements of the form \(am\) where \(a\in I, m\in M\).
-
Prove that \(IM \leq M\) is a submodule.
-
Let \(M, N\) be left \(R{\hbox{-}}\)modules, \(I\) a nilpotent left ideal of \(R\), and \(f: M\to N\) an \(R{\hbox{-}}\)module morphism. Prove that if the induced morphism \(\mkern 1.5mu\overline{\mkern-1.5muf\mkern-1.5mu}\mkern 1.5mu: M/IM \to N/IN\) is surjective, then \(f\) is surjective.
Linear Algebra: Diagonalizability
Fall 2017 #7
Let \(F\) be a field and let \(V\) and \(W\) be vector spaces over \(F\) .
Make \(V\) and \(W\) into \(F[x]{\hbox{-}}\)modules via linear operators \(T\) on \(V\) and \(S\) on \(W\) by defining \(X \cdot v = T (v)\) for all \(v \in V\) and \(X \cdot w = S(w)\) for all w \(\in\) W .
Denote the resulting \(F[x]{\hbox{-}}\)modules by \(V_T\) and \(W_S\) respectively.
-
Show that an \(F[x]{\hbox{-}}\)module homomorphism from \(V_T\) to \(W_S\) consists of an \(F{\hbox{-}}\)linear transformation \(R : V \to W\) such that \(RT = SR\).
-
Show that \(VT \cong WS\) as \(F[x]{\hbox{-}}\)modules \(\iff\) there is an \(F{\hbox{-}}\)linear isomorphism \(P : V \to W\) such that \(T = P^{-1}SP\).
-
Recall that a module \(M\) is simple if \(M \neq 0\) and any proper submodule of \(M\) must be zero. Suppose that \(V\) has dimension 2. Give an example of \(F\), \(T\) with \(V_T\) simple.
-
Assume \(F\) is algebraically closed. Prove that if \(V\) has dimension 2, then any \(V_T\) is not simple.
Spring 2015 #3
Let \(F\) be a field and \(V\) a finite dimensional \(F{\hbox{-}}\)vector space, and let \(A, B: V\to V\) be commuting \(F{\hbox{-}}\)linear maps. Suppose there is a basis \({\mathcal{B}}_1\) with respect to which \(A\) is diagonalizable and a basis \({\mathcal{B}}_2\) with respect to which \(B\) is diagonalizable.
Prove that there is a basis \({\mathcal{B}}_3\) with respect to which \(A\) and \(B\) are both diagonalizable.
Fall 2016 #2
Let \(A, B\) be two \(n\times n\) matrices with the property that \(AB = BA\). Suppose that \(A\) and \(B\) are diagonalizable. Prove that \(A\) and \(B\) are simultaneously diagonalizable.
Spring 2019 #1
Let \(A\) be a square matrix over the complex numbers. Suppose that \(A\) is nonsingular and that \(A^{2019}\) is diagonalizable over \({\mathbf{C}}\).
Show that \(A\) is also diagonalizable over \({\mathbf{C}}\).
- \(A\) is diagonalizable iff \(\min_A(x)\) is separable.
If \(A \in \operatorname{GL}(m, { \mathbf{F} })\) is invertible and \(A^n/{ \mathbf{F} }\) is diagonalizable, then \(A/{ \mathbf{F} }\) is diagonalizable.
-
Let \(A \in \operatorname{GL}(m, { \mathbf{F} })\).
-
Since \(A^n\) is diagonalizable, \(\min_{A^n}(x) \in { \mathbf{F} }[x]\) is separable and thus factors as a product of \(m\) distinct linear factors: \begin{align*} \min_{A^n}(x) = \prod_{i=1}^m (x-\lambda_i), \quad \min_{A^n}(A^n) = 0 \end{align*}
where \(\left\{{\lambda_i}\right\}_{i=1}^m \subset { \mathbf{F} }\) are the distinct eigenvalues of \(A^n\).
-
Moreover \(A\in \operatorname{GL}(m,{ \mathbf{F} }) \implies A^n \in \operatorname{GL}(m,{ \mathbf{F} })\): \(A\) is invertible \(\iff \operatorname{det}(A) = d \in { \mathbf{F} }^{\times}\), and so \(\operatorname{det}(A^n) = \operatorname{det}(A)^n = d^n \in { \mathbf{F} }^{\times}\) using the fact that the determinant is a ring morphism \(\operatorname{det}: \operatorname{Mat}(m\times m) \to{ \mathbf{F} }\) and \({ \mathbf{F} }^{\times}\) is closed under multiplication.
-
So \(A^n\) is invertible, and thus has trivial kernel, and thus zero is not an eigenvalue, so \(\lambda_i \neq 0\) for any \(i\).
-
Since the \(\lambda_i\) are distinct and nonzero, this implies \(x^k\) is not a factor of \(\mu_{A^n}(x)\) for any \(k\geq 0\). Thus the \(m\) terms in the product correspond to precisely \(m\) distinct linear factors.
-
We can now construct a polynomial that annihilates \(A\), namely \begin{align*} q_A(x) \coloneqq\min_{A^n}(x^n) = \prod_{i=1}^m (x^n-\lambda_i) \in { \mathbf{F} }[x], \end{align*}
where we can note that \(q_A(A) = \min_{A^n}(A^n) = 0\), and so \(\min_A(x) \divides q_A(x)\) by minimality.
\(q_A(x)\) has exactly \(nm\) distinct linear factors in \({\mkern 1.5mu\overline{\mkern-1.5mu{ \mathbf{F} }\mkern-1.5mu}\mkern 1.5mu}[x]\)
-
This reduces to showing that no pair \(x^n-\lambda_i, x^n-\lambda_j\) share a root. and that \(x^n-\lambda_i\) does not have multiple roots.
-
For the first claim, we can factor \begin{align*} x^n - \lambda_i = \prod_{k=1}^n (x - \lambda_i^{1\over n} e^{2\pi i k \over n}) \coloneqq\prod_{k=1}^n (x-\lambda^{1\over n} \zeta_n^k) ,\end{align*} where we now use the fact that \(i\neq j \implies \lambda_i^{1\over n} \neq \lambda_j^{1\over n}\). Thus no term in the above product appears as a factor in \(x^n - \lambda_j\) for \(j\neq i\).
-
For the second claim, we can check that \({\frac{\partial }{\partial x}\,}\qty{x^n - \lambda_i} = nx^{n-1}\neq 0\in { \mathbf{F} }\), and \(\gcd(x^n-\lambda_i, nx^{n-1}) = 1\) since the latter term has only the roots \(x=0\) with multiplicity \(n-1\), whereas \(\lambda_i\neq 0 \implies\) zero is not a root of \(x^n-\lambda_i\).
But now since \(q_A(x)\) has exactly distinct linear factors in \(\mkern 1.5mu\overline{\mkern-1.5mu{ \mathbf{F} }\mkern-1.5mu}\mkern 1.5mu[x]\) and \(\min_A(x) \divides q_A(x)\), \(\min_A(x) \in { \mathbf{F} }[x]\) can only have distinct linear factors, and \(A\) is thus diagonalizable over \({ \mathbf{F} }\).
Linear Algebra: Misc
\(\star\) Spring 2012 #6
Let \(k\) be a field and let the group \(G = \operatorname{GL}(m, k) \times\operatorname{GL}(n, k)\) acts on the set of \(m\times n\) matrices \(M_{m, n}(k)\) as follows: \begin{align*} (A, B) \cdot X = AXB^{-1} \end{align*} where \((A, B) \in G\) and \(X\in M_{m, n}(k)\).
-
State what it means for a group to act on a set. Prove that the above definition yields a group action.
-
Exhibit with justification a subset \(S\) of \(M_{m, n}(k)\) which contains precisely one element of each orbit under this action.
\(\star\) Spring 2014 #7
Let \(G = \operatorname{GL}(3, {\mathbf{Q}}[x])\) be the group of invertible \(3\times 3\) matrices over \({\mathbf{Q}}[x]\). For each \(f\in {\mathbf{Q}}[x]\), let \(S_f\) be the set of \(3\times 3\) matrices \(A\) over \({\mathbf{Q}}[x]\) such that \(\operatorname{det}(A) = c f(x)\) for some nonzero constant \(c\in {\mathbf{Q}}\).
-
Show that for \((P, Q) \in G\times G\) and \(A\in S_f\), the formula \begin{align*} (P, Q)\cdot A \coloneqq PAQ^{-1} \end{align*} gives a well defined map \(G\times G \times S_f \to S_f\) and show that this map gives a group action of \(G\times G\) on \(S_f\).
-
For \(f(x) = x^3(x^2+1)^2\), give one representative from each orbit of the group action in (a), and justify your assertion.
Fall 2012 #7
Let \(k\) be a field of characteristic zero and \(A, B \in M_n(k)\) be two square \(n\times n\) matrices over \(k\) such that \(AB - BA = A\). Prove that \(\operatorname{det}A = 0\).
Moreover, when the characteristic of \(k\) is 2, find a counterexample to this statement.
Fall 2012 #8
Prove that any nondegenerate matrix \(X\in M_n({\mathbf{R}})\) can be written as \(X = UT\) where \(U\) is orthogonal and \(T\) is upper triangular.
Fall 2012 #5
Let \(U\) be an infinite-dimensional vector space over a field \(k\), \(f: U\to U\) a linear map, and \(\left\{{u_1, \cdots, u_m}\right\} \subset U\) vectors such that \(U\) is generated by \(\left\{{u_1, \cdots, u_m, f^d(u_1), \cdots, f^d(u_m)}\right\}\) for some \(d\in {\mathbb{N}}\).
Prove that \(U\) can be written as a direct sum \(U \cong V\oplus W\) such that
- \(V\) has a basis consisting of some vector \(v_1, \cdots v_n, f^d(v_1), \cdots, f^d(v_n)\) for some \(d\in {\mathbb{N}}\), and
- \(W\) is finite-dimensional.
Moreover, prove that for any other decomposition \(U \cong V' \oplus W'\), one has \(W' \cong W\).
Fall 2015 #7
-
Show that two \(3\times 3\) matrices over \({\mathbf{C}}\) are similar \(\iff\) their characteristic polynomials are equal and their minimal polynomials are equal.
-
Does the conclusion in (a) hold for \(4\times 4\) matrices? Justify your answer with a proof or counterexample.
Fall 2014 #4
Let \(F\) be a field and \(T\) an \(n\times n\) matrix with entries in \(F\). Let \(I\) be the ideal consisting of all polynomials \(f\in F[x]\) such that \(f(T) =0\).
Show that the following statements are equivalent about a polynomial \(g\in I\):
-
\(g\) is irreducible.
-
If \(k\in F[x]\) is nonzero and of degree strictly less than \(g\), then \(k[T]\) is an invertible matrix.
Fall 2015 #8
Let \(V\) be a vector space over a field \(F\) and \(V {}^{ \vee }\) its dual. A symmetric bilinear form \(({-}, {-})\) on \(V\) is a map \(V\times V\to F\) satisfying \begin{align*} (av_1 + b v_2, w) = a(v_1, w) + b(v_2, w) {\quad \operatorname{and} \quad} (v_1, v_2) = (v_2, v_1) \end{align*} for all \(a, b\in F\) and \(v_1, v_2 \in V\). The form is nondegenerate if the only element \(w\in V\) satisfying \((v, w) = 0\) for all \(v\in V\) is \(w=0\).
Suppose \(({-}, {-})\) is a nondegenerate symmetric bilinear form on \(V\). If \(W\) is a subspace of \(V\), define \begin{align*} W^{\perp} \coloneqq\left\{{v\in V {~\mathrel{\Big\vert}~}(v, w) = 0 \text{ for all } w\in W}\right\} .\end{align*}
-
Show that if \(X, Y\) are subspaces of \(V\) with \(Y\subset X\), then \(X^{\perp} \subseteq Y^{\perp}\).
-
Define an injective linear map \begin{align*} \psi: Y^{\perp}/X^{\perp} \hookrightarrow(X/Y) {}^{ \vee } \end{align*} which is an isomorphism if \(V\) is finite dimensional.
Fall 2018 #4
Let \(V\) be a finite dimensional vector space over a field (the field is not necessarily algebraically closed).
Let \(\phi : V \to V\) be a linear transformation. Prove that there exists a decomposition of \(V\) as \(V = U \oplus W\) , where \(U\) and \(W\) are \(\phi{\hbox{-}}\)invariant subspaces of \(V\) , \({\left.{{\phi}} \right|_{{U}} }\) is nilpotent, and \({\left.{{\phi}} \right|_{{W}} }\) is nonsingular.
\todo[inline]{Revisit.}
Let \(m(x)\) be the minimal polynomial of \(\phi\). If the polynomial \(f(x) = x\) doesn’t divide \(m\), then \(f\) does not have zero as an eigenvalue, so \(\phi\) is nonsingular and since \(0\) is nilpotent, \(\phi + 0\) works.
Otherwise, write \(\phi(x) = x^m \rho(x)\) where \(\gcd(x, \rho(x)) = 1\).
Then \begin{align*} V \cong \frac{k[x]}{m(x)} \cong \frac{k[x]}{(x^m)} \oplus \frac{k[x]}{(\rho)} \coloneqq U \oplus W \end{align*} by the Chinese Remainder theorem.
We can now note that \({\left.{{\phi}} \right|_{{U}} }\) is nilpotent because it has characteristic polynomial \(x^m\), and \({\left.{{\phi}} \right|_{{W}} }\) is nonsingular since \(\lambda = 0\) is not an eigenvalue by construction.
Fall 2018 #5
Let \(A\) be an \(n \times n\) matrix.
-
Suppose that \(v\) is a column vector such that the set \(\{v, Av, . . . , A^{n-1} v\}\) is linearly independent. Show that any matrix \(B\) that commutes with \(A\) is a polynomial in \(A\).
-
Show that there exists a column vector \(v\) such that the set \(\{v, Av, . . . , A^{n-1} v\}\) is linearly independent \(\iff\) the characteristic polynomial of \(A\) equals the minimal polynomial of A.
- Powers of \(A\) commute with polynomials in \(A\).
- The image of a linear map is determined by the image of a basis
- Use Cayley-Hamilton to relate the minimal polynomial to a linear dependence.
- Get a lower bound on the degree of the minimal polynomial.
- Use \(A\curvearrowright k[x]\) to decompose into cyclic \(k[x]{\hbox{-}}\)modules, and use special form of denominators in the invariant factors.
- Reduce to monomials.
Letting \(\mathbf{v}\) be fixed, since \(\left\{{A^j \mathbf{v}}\right\}\) spans \(V\) we have A \begin{align*} B\mathbf{v} = \sum_{j=0}^{n-1}c_j A^j \mathbf{v} .\end{align*}
So let \(p(x) = \sum_{j=0}^{n-1}c_jx^j\). Then consider how \(B\) acts on any basis vector \(A^k \mathbf{v}\).
We have \begin{align*} BA^k \mathbf{v} &= A^k B\mathbf{v} \\ &= A^k p(A) \mathbf{v} \\ &= p(A) A^k \mathbf{v} ,\end{align*}
so \(B = p(A)\) as operators since their actions agree on every basis vector in \(V\).
-
If \(\left\{{A^j \mathbf{v}_k {~\mathrel{\Big\vert}~}0\leq j \leq n-1}\right\}\) is linearly independent, this means that \(A\) does satisfy any polynomial of degree \(d < n\).
-
So \(\deg m_A(x) = n\), and since \(m_A(x)\) divides \(\chi_A(x)\) and both are monic degree polynomials of degree \(n\), they must be equal.
-
Let \(A\curvearrowright k[x]\) by \(A \curvearrowright p(x) \coloneqq p(A)\). This induces an invariant factor decomposition \(V =\cong \bigoplus k[x]/(f_i)\).
-
Since the product of the invariant factors is the characteristic polynomial, the largest invariant factor is the minimal polynomial, and these two are equal, there can only be one invariant factor and thus the invariant factor decomposition is \begin{align*} V\cong \frac{k[x]}{(\chi_A(x))} \end{align*} as an isomorphism of \(k[x]{\hbox{-}}\)modules.
-
So \(V\) is a cyclic \(k[x]\) module, which means that \(V = k[x]\curvearrowright\mathbf{v}\) for some \(\mathbf{v}\in V\) such that \(\operatorname{Ann}(\mathbf{v}) = \chi_A(x)\), i.e. there is some element \(\mathbf{v}\in V\) whose orbit is all of \(V\).
-
But then noting that monomials span \(k[x]\) as a \(k{\hbox{-}}\)module, we can write \begin{align*} V &\cong k[x] \curvearrowright\mathbf{v} \\ &\coloneqq\left\{{f(x) \curvearrowright\mathbf{v} {~\mathrel{\Big\vert}~}f \in k[x]}\right\} \\ &= \mathop{\mathrm{span}}_k \left\{{x^k \curvearrowright\mathbf{v} {~\mathrel{\Big\vert}~}k \geq 0}\right\} \\ &\coloneqq\mathop{\mathrm{span}}_k \left\{{A^k\mathbf{v} {~\mathrel{\Big\vert}~}k \geq 0}\right\} ,\end{align*} where we’ve used that \(x\) acts by \(A\) and thus \(x^k\) acts by \(A^k\).
-
Moreover, we can note that if \(\ell \geq \deg \chi_A(x)\), then \(A^\ell\) is a linear combination of \(\left\{{A^j \mathrel{\Big|}0 \leq j \leq n-1}\right\}\), and so \begin{align*} V &\cong \mathop{\mathrm{span}}_k \left\{{A^\ell\mathbf{v} {~\mathrel{\Big\vert}~}\ell \geq 0}\right\} \\ &= \mathop{\mathrm{span}}_k \left\{{A^\ell \mathbf{v} {~\mathrel{\Big\vert}~}1 \leq \ell \leq n-1}\right\} .\end{align*}
Fall 2019 #8
Let \(\{e_1, \cdots, e_n \}\) be a basis of a real vector space \(V\) and let \begin{align*} \Lambda \coloneqq\left\{{ \sum r_i e_i \mathrel{\Big|}r_i \in {\mathbf{Z}}}\right\} \end{align*}
Let \(\cdot\) be a non-degenerate (\(v \cdot w = 0\) for all \(w \in V \iff v = 0\)) symmetric bilinear form on \(V\) such that the Gram matrix \(M = (e_i \cdot e_j )\) has integer entries.
Define the dual of \(\Lambda\) to be \begin{align*} \Lambda {}^{ \vee }\coloneqq\{v \in V {~\mathrel{\Big\vert}~}v \cdot x \in {\mathbf{Z}}\text{ for all } x \in \Lambda \} .\end{align*}
-
Show that \(\Lambda \subset \Lambda {}^{ \vee }\).
-
Prove that \(\operatorname{det}M \neq 0\) and that the rows of \(M^{-1}\) span \(\Lambda {}^{ \vee }\).
- Prove that \(\operatorname{det}M = |\Lambda {}^{ \vee }/\Lambda|\).
\todo[inline]{Todo, missing part (c).}
-
Let \(\mathbf{v} \in \Lambda\), so \(\mathbf{v} = \sum_{i=1}^n r_i \mathbf{e}_i\) where \(r_i \in {\mathbf{Z}}\) for all \(i\).
-
Then if \(\mathbf{x} = \sum_{j=1}^n s_j \mathbf{e}_j \in \Lambda\) is arbitrary, we have \(s_j \in {\mathbf{Z}}\) for all \(j\) and \begin{align*} {\left\langle {\mathbf{v}},~{\mathbf{x}} \right\rangle} &= {\left\langle {\sum_{i=1}^n r_i \mathbf{e}_i},~{\sum_{j=1}^n s_j \mathbf{e}_j } \right\rangle} \\ &= \sum_{i=1}^n \sum_{j=1}^n r_i s_j {\left\langle {\mathbf{e}_i},~{\mathbf{e}_j } \right\rangle} \in {\mathbf{Z}} \end{align*} since this is a sum of products of integers (since \({\left\langle {\mathbf{e}_i},~{\mathbf{e}_j} \right\rangle} \in {\mathbf{Z}}\) for each \(i, j\) pair by assumption) so \(\mathbf{v} \in \Lambda {}^{ \vee }\) by definition.
The determinant is nonzero.
-
Suppose \(\operatorname{det}M = 0\). Then \(\ker M \neq \mathbf{0}\), so let \(\mathbf{v} \in \ker M\) be given by \(\mathbf{v} = \sum_{i=1}^n v_i \mathbf{e}_i \neq \mathbf{0}\).
-
Note that \begin{align*} M\mathbf{v} = 0 &\implies \left[ \begin{array}{ccc} \mathbf{e}_1 \cdot \mathbf{e}_1 & \mathbf{e}_1 \cdot \mathbf{e}_2 & \cdots \\ \mathbf{e}_2 \cdot \mathbf{e}_1 & \mathbf{e}_2 \cdot \mathbf{e}_2 & \cdots \\ \vdots & \vdots & \ddots \end{array} \right] \left[\begin{array}{c} v_1 \\ v_2 \\ \vdots \end{array}\right] = \mathbf{0} \\ \\ &\implies \sum_{j=1}^n v_j{\left\langle {\mathbf{e}_k},~{\mathbf{e}_j} \right\rangle} = 0 {\quad \operatorname{for each fixed} \quad} k .\end{align*}
-
We can now note that \({\left\langle {\mathbf{e}_k},~{\mathbf{v}} \right\rangle} = \sum_{j=1}^n v_j {\left\langle {\mathbf{e}_k},~{\mathbf{e}_j} \right\rangle} = 0\) for every \(k\) by the above observation, which forces \(\mathbf{v} = 0\) by non-degeneracy of \({\left\langle {{-}},~{{-}} \right\rangle}\), a contradiction.
???
\todo[inline]{Missing work!}
Write \(M = A^tA\) where \(A\) has the \(\mathbf{e}_i\) as columns. Then \begin{align*} M\mathbf{x} = 0 &\implies A^t A \mathbf{x} = 0 \\ &\implies \mathbf{x}^t A^t A \mathbf{x} = 0 \\ &\implies {\left\lVert {A \mathbf{x}} \right\rVert}^2 = 0 \\ &\implies A\mathbf{x} = 0 \\ &\implies \mathbf{x} = 0 ,\end{align*}
since \(A\) has full rank because the \(\mathbf{e}_i\) are linearly independent.
Let \(A = [\mathbf{e}_1^t, \cdots, \mathbf{e}_n^t]\) be the matrix with \(\mathbf{e}_i\) in the \(i\)th column.
The rows of \(A^{-1}\) span \(\Lambda {}^{ \vee }\). Equivalently, the columns of \(A^{-t}\) span \(\Lambda {}^{ \vee }\).
-
Let \(B = A^{-t}\) and let \(\mathbf{b}_i\) denote the columns of \(B\), so \(\operatorname{im}B = \mathop{\mathrm{span}}{\left\{{\mathbf{b}_i}\right\}}\).
-
Since \(A \in \operatorname{GL}(n, {\mathbf{Z}})\), \(A^{-1}, A^t, A^{-t} \in \operatorname{GL}(n, {\mathbf{Z}})\) as well. \begin{align*} \mathbf{v} \in \Lambda {}^{ \vee } &\implies {\left\langle {\mathbf{e}_i},~{\mathbf{v}} \right\rangle} = z_i \in {\mathbf{Z}}\quad \forall i \\ &\implies A^t \mathbf{v} = \mathbf{z} \coloneqq[z_1, \cdots, z_n] \in {\mathbf{Z}}^n \\ &\implies \mathbf{v} = A^{-t} \mathbf{z} \coloneqq B\mathbf{z} \in \operatorname{im}B \\ &\implies \mathbf{v} \in \operatorname{im}B \\ &\implies \Lambda {}^{ \vee }\subseteq \operatorname{im}B ,\end{align*} and \begin{align*} B^t A = (A^{-t})^t A = A^{-1}A = I \\ \implies \mathbf{b}_i \cdot \mathbf{e}_j = \delta_{ij} \in {\mathbf{Z}}\\ \implies \operatorname{im}B \subseteq \mathop{\mathrm{span}}~ \Lambda {}^{ \vee } .\end{align*}
Spring 2013 #6
Let \(V\) be a finite dimensional vector space over a field \(F\) and let \(T: V\to V\) be a linear operator with characteristic polynomial \(f(x) \in F[x]\).
-
Show that \(f(x)\) is irreducible in \(F[x] \iff\) there are no proper nonzero subspaces \(W< V\) with \(T(W) \subseteq W\).
-
If \(f(x)\) is irreducible in \(F[x]\) and the characteristic of \(F\) is 0, show that \(T\) is diagonalizable when we extend the field to its algebraic closure.
\todo[inline]{Is there a proof without matrices? What if $V$ is infinite dimensional?}
\todo[inline]{How to extend basis?}
-
Every \(\mathbf{v}\in V\) is \(T{\hbox{-}}\)cyclic \(\iff \chi_T(x)/{\mathbf{k}}\) is irreducible.
- \(\implies\): Same as argument below.
- \(\impliedby\): Suppose \(f\) is irreducible, then \(f\) is equal to the minimal polynomial of \(T\).
- Characterization of diagonalizability: \(T\) is diagonalizable over \(F \iff \min_{T, F}\) is squarefree in \(\mkern 1.5mu\overline{\mkern-1.5muF\mkern-1.5mu}\mkern 1.5mu[x]\)?
Let \(f\) be the characteristic polynomial of \(T\).
\(\implies\):
- By contrapositive, suppose there is a proper nonzero invariant subspace \(W<V\) with \(T(W) \subseteq W\), we will show the characteristic polynomial \(f \coloneqq\chi_{V, T}(x)\) is reducible.
- Since \(T(W)\subseteq W\), the restriction \(g\coloneqq\chi_{V, T}(x) \mathrel{\Big|}_W: W\to W\) is a linear operator on \(W\).
\(g\) divides \(f\) in \({ \mathbf{F} }[x]\) and \(\deg(g) < \deg(f)\).
-
Choose an ordered basis for \(W\), say \({\mathcal{B}}_W \coloneqq\left\{{\mathbf{w}_1, \cdots, \mathbf{w}_k}\right\}\) where \(k=\dim_F(W)\)
-
Claim: this can be extended to a basis of \(V\), say \({\mathcal{B}}_V \coloneqq\left\{{\mathbf{w}_1, \cdots, \mathbf{w}_k, \mathbf{v}_1, \cdots, \mathbf{v}_j}\right\}\) where \(k+j = \dim_F(V)\).
- Note that since \(W<V\) is proper, \(j\geq 1\).
-
Restrict \(T\) to \(W\) to get \(T_W\), then let \(B = [T_W]_{{\mathcal{B}}_W}\) be the matrix representation of \(T_W\) with respect to \({\mathcal{B}}_W\).
-
Now consider the matrix representation \([T]_{{\mathcal{B}}_V}\), in block form this is given by \begin{align*} [T]_{{\mathcal{B}}_V} = \begin{bmatrix} B & C \\ 0 & D \end{bmatrix} \end{align*} where we’ve used that \(W<V\) is proper to get the existence of \(C, D\) (there is at least one additional row/column since \(j\geq 1\) in the extended basis.)
\todo[inline]{Why?} -
Now expand along the first column block to obtain \begin{align*} \chi_{T, V}(x) \coloneqq\operatorname{det}([T]_{{\mathcal{B}}_V} - xI) = \operatorname{det}(B - xI)\cdot \operatorname{det}(D - xI) \coloneqq\chi_{T, W}(x) \cdot \operatorname{det}(D-xI) .\end{align*}
-
Claim: \(\operatorname{det}(D - xI) \in xF[x]\) is nontrivial
-
The claim follows because this forces \(\deg(\operatorname{det}(D-xI)) \geq 1\) and so \(\chi_{T, W}(x)\) is a proper divisor of \(\chi_{T, V}(x)\).
-
Thus \(f\) is reducible.
\(\impliedby\)
- Suppose \(f\) is reducible, then we will produce a proper \(T{\hbox{-}}\)invariant subspace.
- Claim: if \(f\) is reducible, there exists a nonzero, noncyclic vector \(\mathbf{v}\).
- Then \(\mathop{\mathrm{span}}_k\left\{{T^j\mathbf{v}}\right\}_{j=1}^d\) is a \(T{\hbox{-}}\)invariant subspace that is nonzero, and not the entire space since \(\mathbf{v}\) is not cyclic.
- Let \(\min_{T, F}(x)\) be the minimal polynomial of \(T\) and \(\chi_{T, F}(x)\) be its characteristic polynomial.
- By Cayley-Hamilton, \(\min_{T, F}(x)\) divides \(\chi_{T, F}\)
- Since \(\chi_{T, F}\) is irreducible, these polynomials are equal.
- Claim: \(T/F\) is diagonalizable \(\iff \min_{T, F}\) splits over \(F\) and is squarefree.
- Replace \(F\) with its algebraic closure, then \(\min_{T, F}\) splits.
-
Claim: in characteristic zero, every irreducible polynomial is separable
- Proof: it must be the case that either \(\gcd(f, f') = 1\) or \(f' \equiv 0\), where the second case only happens in characteristic \(p>0\).
- The first case is true because \(\deg f' < \deg f\), and if \(\gcd(f, f') = p\), then \(\deg p < \deg f\) and \(p\divides f\) forces \(p=1\) since \(f\) is irreducible.
- So \(\min_{T, F}\) splits into distinct linear factors
- Thus \(T\) is diagonalizable.
Fall 2020 #8
Let \(A\in \operatorname{Mat}(n\times n, {\mathbf{C}})\) such that the group generated by \(A\) under multiplication is finite. Show that \begin{align*} \operatorname{Tr}(A^{-1}) ={\overline{{\operatorname{Tr}(A) }}} ,\end{align*} where \({\overline{{({-})}}}\) denotes taking the complex conjugate and \(\operatorname{Tr}({-})\) is the trace.
Linear Algebra: Canonical Forms
Fall 2021 #3
What is the Jordan normal form over \(\mathbb{C}\) of a \(7 \times 7\) matrix \(A\) which satisfies all of the following conditions:
-
\(A\) has real coefficients,
-
\(\mathrm{rk} A=5\),
-
\(\mathrm{rk} A^{2}=4\),
-
\(\mathrm{rk} A-I=6\),
-
\(\mathrm{rk} A^{3}-I=4\),
-
\(\operatorname{tr} A=1 ?\)
-
We’ll use rank-nullity throughout: \(\operatorname{rank}M + \dim \ker M = 7\).
-
Also note that \begin{align*} Av = \lambda v \implies A^nv = A^{n-1}Av = A^{n-1}\lambda v = \cdots = \lambda^n v ,\end{align*} so if \(\lambda \in \operatorname{Spec}(A)\) then \(\lambda^n\in \operatorname{Spec}(A^n)\). Conversely, \(\lambda\in \operatorname{Spec}(A^n) \implies \lambda^{1\over n}\in \operatorname{Spec}(A)\), which we’ll use several times.
-
Since \(5 = \operatorname{rank}A = \operatorname{rank}(A - 0\cdot I)\), we have \(\dim \ker(A-0\cdot I) = 2\) contributing an eigenvalue of \(\lambda = 0\) with multiplicity \(2\).
-
Since \(4 = \operatorname{rank}A^2 = \operatorname{rank}(A^2 - 0\cdot \lambda) = \operatorname{rank}(A-0\cdot \lambda)^2\), we have that \(\dim \ker(A-0\cdot I)^2 = 3\). Since \(\dim \ker (A-0\cdot I)^1 = 2 < 3\), this means there is 1 generalized eigenvector associated to \(\lambda = 0\).
-
Since \(6 = \operatorname{rank}(A-1\cdot I)\), \(\dim \ker (A- 1\cdot I) = 1\), contributing \(\lambda = 1\) with multiplicity 1.
-
Since \(\operatorname{rank}(A^3-1\cdot I) = 4\), we have \(\dim \ker (A^3-1\cdot I) = 3\), contributing \(\lambda = 1\) now to \(\operatorname{Spec}(A^3)\) instead of \(\operatorname{Spec}(A)\). Thus some unknown cube roots of 1 are contributed to \(\operatorname{Spec}(A)\), so any of \(1=\zeta_3^0, \zeta_3, \zeta_3^2\) are possibilities at this point. Call these three contributions \(z_1, z_2, z_3\), which may not be distinct.
-
Now use that \({\mathrm{tr}}(A) = \sum_{i=1}^n \lambda_i\) is the sum of the diagonal on \(\operatorname{JCF}(A)\), using that trace is a similarity invariant, to write \begin{align*} 1 = {\mathrm{tr}}(A) = (0 + 0) + (0) + (1) + (z_1 + z_2 + z_3) \implies z_1 + z_2 + z_3 = 0 ,\end{align*} which is actually enough to force \(z_1 = 1, z_2 = \zeta_3, z_3 = \zeta_3^2\), since no other combination sums to zero. That \(1 + \zeta_3 + \zeta_3^2 = 0\) is a general fact.
-
Since \(\lambda=1\) occurs twice as an eigenvalue but \(\dim \ker(A-1\cdot I) = 1\), the two copies of \(\lambda = 1\) must occur in a nontrivial Jordan block.
-
So we get a Jordan form \begin{align*} \operatorname{JCF}(A) = \begin{bmatrix} 0 & & & & & & \\ & 0 & 1 & & & & \\ & & 0 & & & & \\ & & & 1 & 1 & & \\ & & & & 1 & & \\ & & & & & \zeta_3 & \\ & & & & & & \zeta_3^2 \\ \end{bmatrix} .\end{align*}
\(\star\) Spring 2012 #8
Let \(V\) be a finite-dimensional vector space over a field \(k\) and \(T:V\to V\) a linear transformation.
-
Provide a definition for the minimal polynomial in \(k[x]\) for \(T\).
-
Define the characteristic polynomial for \(T\).
- Prove the Cayley-Hamilton theorem: the linear transformation \(T\) satisfies its characteristic polynomial.
\(\star\) Spring 2020 #8
Let \(T:V\to V\) be a linear transformation where \(V\) is a finite-dimensional vector space over \({\mathbf{C}}\). Prove the Cayley-Hamilton theorem: if \(p(x)\) is the characteristic polynomial of \(T\), then \(p(T) = 0\). You may use canonical forms.
\(\star\) Spring 2012 #7
Consider the following matrix as a linear transformation from \(V\coloneqq{\mathbf{C}}^5\) to itself: \begin{align*} A=\left(\begin{array}{ccccc} -1 & 1 & 0 & 0 & 0 \\ -4 & 3 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 2 \end{array}\right) .\end{align*}
-
Find the invariant factors of \(A\).
-
Express \(V\) in terms of a direct sum of indecomposable \({\mathbf{C}}[x]{\hbox{-}}\)modules.
- Find the Jordan canonical form of \(A\).
Fall 2019 Final #8
Exhibit the rational canonical form for
- \(A\in M_6({\mathbf{Q}})\) with minimal polynomial \((x-1)(x^2 + 1)^2\).
- \(A\in M_{10}({\mathbf{Q}})\) with minimal polynomial \((x^2+1)^2(x^3 + 1)\).
Fall 2019 Final #9
Exhibit the rational and Jordan canonical forms for the following matrix \(A\in M_4({\mathbf{C}})\): \begin{align*} A=\left(\begin{array}{cccc} 2 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ -2 & -2 & 0 & 1 \\ -2 & 0 & -1 & -2 \end{array}\right) .\end{align*}
Spring 2016 #7
Let \(D = {\mathbf{Q}}[x]\) and let \(M\) be a \({\mathbf{Q}}[x]{\hbox{-}}\)module such that \begin{align*} M \cong \frac{\mathbb{Q}[x]}{(x-1)^{3}} \oplus \frac{\mathbb{Q}[x]}{\left(x^{2}+1\right)^{3}} \oplus \frac{\mathbb{Q}[x]}{(x-1)\left(x^{2}+1\right)^{5}} \oplus \frac{\mathbb{Q}[x]}{(x+2)\left(x^{2}+1\right)^{2}} .\end{align*}
Determine the elementary divisors and invariant factors of \(M\).
Spring 2020 #7
Let \begin{align*} A=\left[\begin{array}{ccc} 2 & 0 & 0 \\ 4 & 6 & 1 \\ -16 & -16 & -2 \end{array}\right] \in M_{3}(\mathrm{C}) .\end{align*}
-
Find the Jordan canonical form \(J\) of \(A\).
-
Find an invertible matrix \(P\) such that \(P^{-1}A P = J\).
- Write down the minimal polynomial of \(A\).
You should not need to compute \(P^{-1}\).
Spring 2019 #7
Let \(p\) be a prime number. Let \(A\) be a \(p \times p\) matrix over a field \(F\) with 1 in all entries except 0 on the main diagonal.
Determine the Jordan canonical form (JCF) of \(A\)
-
When \(F = {\mathbf{Q}}\),
-
When \(F = { \mathbf{F} }_p\).
Hint: In both cases, all eigenvalues lie in the ground field. In each case find a matrix \(P\) such that \(P^{-1}AP\) is in JCF.
- Work with matrix of all ones instead.
- Eyeball eigenvectors.
- Coefficients in minimal polynomial: size of largest Jordan block
- Dimension of eigenspace: number of Jordan blocks
- We can always read off the characteristic polynomial from the spectrum.
- Todo
Proof of (a): Let \(A\) be the matrix in the question, and \(B\) be the matrix containing 1’s in every entry.
-
Noting that \(B = A+I\), we have \begin{align*} &B\mathbf{x} = \lambda \mathbf{x} \\ &\iff (A+I) \mathbf{x} = \lambda \mathbf{x} \\ &\iff A \mathbf{x} = (\lambda - 1) \mathbf{x} ,\end{align*} so we will find the eigenvalues of \(B\) and subtract one from each.
-
Note that \(B\mathbf{v} = {\left[ {\sum v_i, \sum v_i, \cdots, \sum v_i} \right]}\), i.e. it has the effect of summing all of the entries of \(\mathbf{v}\) and placing that sum in each component.
-
We proceed by finding \(p\) eigenvectors and eigenvalues, since the JCF and minimal polynomials will involve eigenvalues and the transformation matrix will involve (generalized) eigenvectors.
Each vector of the form \(\mathbf{p}_i \coloneqq\mathbf{e}_1 - \mathbf{e}_{i+1} = {\left[ {1, 0, 0,\cdots, 0 -1, 0, \cdots, 0 } \right]}\) where \(i\neq j\) is also an eigenvector with eigenvalues \(\lambda_0 = 0\), and this gives \(p-1\) linearly independent vectors spanning the eigenspace \(E_{\lambda_0}\)
\(\mathbf{v}_1 = {\left[ {1, 1, \cdots, 1} \right]}\) is an eigenvector with eigenvalue \(\lambda_1 = p\).
-
Using that the eigenvalues of \(A\) are \(1+\lambda_i\) for \(\lambda_i\) the above eigenvalues for \(B\), \begin{align*} \operatorname{Spec}(B) \coloneqq\left\{{(\lambda_i, m_i)}\right\} &= \left\{{(p, 1), (0, p-1)}\right\} \implies \chi_{B}(x) = (x-p)x^{p-1} \\ \implies \operatorname{Spec}(A) &= \left\{{(p-1,1), (-1, p-1) }\right\} \implies \chi_{A}(x) = (x- p+1)(x+1)^{p-1} \\ \end{align*}
-
The dimensions of eigenspaces are preserved, thus ` \begin{align*} JCF_{\mathbf{Q}}(A) = J_{p-1}^{1} \oplus (p-1)J_{-1}^1
\left[\begin{array}{r|r|r|r|r|r} p-1 & 0 & 0 & \cdots & 0 & 0 \ \hline 0& -1 & 0 & 0 & 0 & 0 \ \hline 0& 0 & -1 & 0 & 0 & 0 \ \hline 0& 0 & 0 & \ddots & \ddots & 0 \ \hline 0& 0 & 0 & \cdots & -1 & 0 \ \hline 0& 0 & 0 & \cdots & 0 & -1 \ \end{array}\right] .\end{align*} `{=html}
-
The matrix \(P\) such that \(A = PJP^{-1}\) will have columns the bases of the generalized eigenspaces.
-
In this case, the generalized eigenspaces are the usual eigenspaces, so \begin{align*} P = [\mathbf{v}_1, \mathbf{p}_1, \cdots, \mathbf{p}_{p-1}] = \left[\begin{array}{rrrrrr} 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & -1 & 0 & 0 & 0 & 0 \\ 1 & 0 & -1 & 0 & 0 & 0 \\ 1 & 0 & 0 & -1 & 0 & 0 \\ 1 & \vdots & \vdots & \vdots & \ddots & \vdots\\ 1 & 0 & 0 & 0 & 0 & -1 \\ \end{array}\right] .\end{align*}
- Compute \begin{align*}B \mathbf{p}_i = {\left[ { 1 + 0 + \cdots + 0 + (-1) + 0 + \cdots + 0} \right]} = {\left[ {0, 0, \cdots, 0} \right]}\end{align*}
- So every \(\mathbf{p}_i \in \ker(B)\), so they are eigenvectors with eigenvalue 0.
- Since the first component is fixed and we have \(p-1\) choices for where to place a \(-1\), this yields \(p-1\) possibilities for \(\mathbf{p}_i\)
- These are linearly independent since the \((p-1)\times (p-1)\) matrix \({\left[ { \mathbf{p}_1^t, \cdots, \mathbf{p}_{p-1}^t} \right]}\) satisfies \begin{align*} \operatorname{det} \begin{bmatrix} 1 & 1 & 1 & \cdots & 1\\ -1 & 0 & 0 & \cdots & 0\\ 0 & -1 & 0 & \cdots & 0\\ 0 & 0 & -1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & -1\\ \end{bmatrix} &= (1) \cdot \operatorname{det} \begin{bmatrix} -1 & 0 & 0 & \cdots & 0\\ 0 & -1 & 0 & \cdots & 0\\ 0 & 0 & -1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & -1\\ \end{bmatrix} \\ &= (-1)^{p-2} \neq 0 .\end{align*}
where the first equality follows from expanding along the first row and noting this is the first minor, and every other minor contains a row of zeros.
- Compute \begin{align*}B\mathbf{v} = {\left[ {\sum_{i=1}^p 1, \sum_{i=1}^p 1, \cdots, \sum_{i=1}^p 1} \right]} = {\left[ {p, p, \cdots, p} \right]} = p {\left[ {1, 1, \cdots, 1} \right]} = p\mathbf{v}_1,\end{align*} thus \(\lambda_1 = p\)
- \(\dim E_{\lambda_1} = 1\) since the eigenspaces are orthogonal and \(E_{\lambda_0} \oplus E_{\lambda_1} \leq F^p\) is a subspace, so \(p > \dim(E_{\lambda_0}) + \dim E_{\lambda_1} = p-1 + \dim E_{\lambda_1}\) and it isn’t zero dimensional.
Proof of (b):
For \(F = { \mathbf{F} }_p\), all eigenvalues/vectors still lie in \({ \mathbf{F} }_p\), but now \(-1 = p-1\), making \((x-(p-1))(x+1)^{p-1} = (x+1)(x+1)^{p-1}\), so \(\chi_{A, { \mathbf{F} }_p}(x) = (x+1)^p\), and the Jordan blocks may merge.
-
A computation shows that \((A+I)^2 = pA = 0 \in M_p({ \mathbf{F} }_p)\) and \((A+I) \neq 0\), so \(\min_{A, { \mathbf{F} }_p}(x) = (x+1)^2\).
- Thus the largest Jordan block corresponding to \(\lambda = -1\) is of size 2
-
Can check that \(\operatorname{det}(A) = \pm 1 \in { \mathbf{F} }_p^{\times}\), so the vectors \(\mathbf{e}_1 - \mathbf{e}_i\) are still linearly independent and thus \(\dim E_{-1} = p-1\)
- So there are \(p-1\) Jordan blocks for \(\lambda = 0\).
Summary: \begin{align*} \min_{A, { \mathbf{F} }_p}(x) &= (x+1)^2 \\ \chi_{A, { \mathbf{F} }_p}(x) &\equiv (x+1)^p \\ \dim E_{-1} &= p-1 .\end{align*}
Thus \begin{align*} JCF_{{ \mathbf{F} }_p}(A) = J_{-1}^{2} \oplus (p-2)J_{-1}^1 = \left[\begin{array}{rr|r|r|r|r} -1 & 1 & 0 & \cdots & 0 & 0 \\ 0& -1 & 0 & 0 & 0 & 0 \\ \hline 0& 0 & -1 & 0 & 0 & 0 \\ \hline 0& 0 & 0 & \ddots & \ddots & 0 \\ \hline 0& 0 & 0 & \cdots & -1 & 0 \\ \hline 0& 0 & 0 & \cdots & 0 & -1 \\ \end{array}\right] .\end{align*}
To obtain a basis for \(E_{\lambda = 0}\), first note that the matrix \(P = [\mathbf{v}_1, \mathbf{p}_1, \cdots , \mathbf{p}_{p-1}]\) from part (a) is singular over \({ \mathbf{F} }_p\), since \begin{align*} \mathbf{v}_1 + \mathbf{p}_1 + \mathbf{p}_2 + \cdots + \mathbf{p}_{p-2} &= [p-1, 0, 0, \cdots, 0, 1] \\ &= [-1, 0,0,\cdots, 0, 1] \\ &= - \mathbf{p}_{p-1} .\end{align*}
We still have a linearly independent set given by the first \(p-1\) columns of \(P\), so we can extend this to a basis by finding one linearly independent generalized eigenvector.
Solving \((A-I\lambda)\mathbf{x} = \mathbf{v}_1\) is our only option (the others won’t yield solutions). This amounts to solving \(B\mathbf{x} = \mathbf{v}_1\), which imposes the condition \(\sum x_i = 1\), so we can choose \(\mathbf{x} = [1, 0, \cdots, 0]\).
Thus \begin{align*} P = [\mathbf{v}_1, \mathbf{x}, \mathbf{p}_1, \cdots, \mathbf{p}_{p-2}] = \left[\begin{array}{rrrrrr} 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 0 & -1 & 0 & 0 & 0 \\ 1 & 0 & 0 & -1 & 0 & 0 \\ 1 & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & 0 & 0 & 0 & 0 & -1\\ 1 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\right] .\end{align*}
Spring 2018 #4
Let \begin{align*} A=\left[\begin{array}{lll}{0} & {1} & {-2} \\ {1} & {1} & {-3} \\ {1} & {2} & {-4}\end{array}\right] \in M_{3}(\mathbb{C}) \end{align*}
-
Find the Jordan canonical form \(J\) of \(A\).
-
Find an invertible matrix \(P\) such that \(P^{-1}AP = J\).
You should not need to compute \(P^{-1}\).
Spring 2017 #6
Let \(A\) be an \(n\times n\) matrix with all entries equal to \(0\) except for the \(n-1\) entries just above the diagonal being equal to 2.
-
What is the Jordan canonical form of \(A\), viewed as a matrix in \(M_n({\mathbf{C}})\)?
-
Find a nonzero matrix \(P\in M_n({\mathbf{C}})\) such that \(P^{-1}A P\) is in Jordan canonical form.
Spring 2016 #1
Let \begin{align*} A=\left(\begin{array}{ccc} -3 & 3 & -2 \\ -7 & 6 & -3 \\ 1 & -1 & 2 \end{array}\right) \in M_{3}(\mathrm{C}) .\end{align*}
-
Find the Jordan canonical form \(J\) of \(A\).
-
Find an invertible matrix \(P\) such that \(P^{-1}A P = J\). You do not need to compute \(P^{-1}\).
Spring 2015 #6
Let \(F\) be a field and \(n\) a positive integer, and consider \begin{align*} A=\left[\begin{array}{ccc} 1 & \dots & 1 \\ & \ddots & \\ 1 & \dots & 1 \end{array}\right] \in M_{n}(F) .\end{align*}
Show that \(A\) has a Jordan normal form over \(F\) and find it.
Hint: treat the cases \(n\cdot 1 \neq 0\) in \(F\) and \(n\cdot 1 = 0\) in \(F\) separately.
Fall 2014 #5
Let \(T\) be a \(5\times 5\) complex matrix with characteristic polynomial \(\chi(x) = (x-3)^5\) and minimal polynomial \(m(x) = (x-3)^2\). Determine all possible Jordan forms of \(T\).
Spring 2013 #5
Let \(T: V\to V\) be a linear map from a 5-dimensional \({\mathbf{C}}{\hbox{-}}\)vector space to itself and suppose \(f(T) = 0\) where \(f(x) = x^2 + 2x + 1\).
-
Show that there does not exist any vector \(v\in V\) such that \(Tv = v\), but there does exist a vector \(w\in V\) such that \(T^2 w= w\).
-
Give all of the possible Jordan canonical forms of \(T\).
Spring 2021 #1
Let m \begin{align*} A \coloneqq \begin{bmatrix} 4 & 1 & -1 \\ -6 & -1 & 2 \\ 2 & 1 & 1 \end{bmatrix} \in \operatorname{Mat}(3\times 3, {\mathbf{C}}) .\end{align*}
-
Find the Jordan canonical form \(J\) of \(A\).
-
Find an invertible matrix \(P\) such that \(J = P ^{-1}A P\).
- Write down the minimal polynomial of \(A\).
You should not need to compute \(P^{-1}\)
- \(\chi_A(t) = t^n - {\mathrm{tr}}\qty{\bigwedge\nolimits^1 A}t^{n-1} + {\mathrm{tr}}\qty{\bigwedge\nolimits^2 A}t^{n-2} - \cdots \pm \operatorname{det}(A)\)
- Finding generalized eigenvectors: let \(B = A-\lambda I\), get eigenvector \(v\), solve \(Bw_1 = v, Bw_2 = w_1, \cdots\) to get a Jordan block. Repeat with any other usual eigenvectors.
- Convention: construct Jordan blocks in decreasing order of magnitude of eigenvalues.
-
Polynomial exponent data:
- Minimal polynomial exponents: sizes of largest Jordan blocks.
- Characteristic polynomial exponents: sum of sizes of Jordan blocks, i.e. how many times \(\lambda\) is on the diagonal of \(\operatorname{JCF}(A)\).
-
Write \(\chi_A(t) = t^3 - T_1 t^2 + T_2 t - T_3\) where \(T_i \coloneqq{\mathrm{tr}}\qty{\bigwedge\nolimits^i A}\):
- \(T_1 = {\mathrm{tr}}(A) = 4-1+1=4\).
- \(T_2 = (-1-2) + (4+2) + (-4-6) = 5\).
- \(T_3 = \operatorname{det}(A) = 4(-1-2) -1(-10) + (-1)(-6+2) = 2\).
- So \(\chi_A(t) = t^3 - 4t^2 + 5t-2\).
- Try rational roots test: \(r \in \left\{{\pm 2/1}\right\}\), and check that 2 is root.
- By polynomial long division, \(\chi_A(t) / (t-2) = t^2-2t+1 = (t-1)^2\).
- So the eigenvalues are \(\lambda = 2, 1\).
-
\(\lambda = 2\):
- Set \(U\coloneqq A-\lambda I\), then find \(\operatorname{RREF}(U)\) to compute its kernel: \begin{align*} U \coloneqq \begin{bmatrix} 2 & 1 & -1 \\ -6 & -3 & 2 \\ 2 & 1 & -1 \end{bmatrix} \leadsto \begin{bmatrix} 2 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix} ,\end{align*} which yields \(v_1 = [1,-2,0]\).
-
\(\lambda = 2\):
-
Similarly, \begin{align*} U \coloneqq \begin{bmatrix} 3 & 1 & -1 \\ -6 & -2 & 2 \\ 2 & 1 & 0 \end{bmatrix} \leadsto \begin{bmatrix} 1 & 0 & -1 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end{bmatrix} ,\end{align*} which yields \(v_2 = [1,-2,1]\).
-
Solve \(Uw = v_3\): \begin{align*} \begin{bmatrix} 3 & 1 & -1 & 1 \\ -6 & -2 & 2 & -2 \\ 2 & 1 & 0 & 1 \end{bmatrix} \leadsto \begin{bmatrix} 1 & 0 & -1 & 0 \\ 0 & 1 & 2 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix} ,\end{align*} so take \(v_3 = [0,1,0]\).
-
- Putting things together: \begin{align*} A &= P^{-1}J P \text{ where } \\ J = J_1(\lambda = 2) \oplus J_2(\lambda = 1) &= \begin{bmatrix} 2 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix} \\ P = [v_1, v_2, v_3] &= \begin{bmatrix} 1 & 1 & 0 \\ -2 & -2 & 1 \\ 0 & 1 & 0 \end{bmatrix} .\end{align*}
- Write \(\min_A(t) = (t-2)(t-1)^{\ell_1}\), then since \(\min_A(t)\) divides \(\chi_A(t)\) either \(\ell_1 = 1, 2\).
- \(\ell_1\) is the size of the largest block corresponding to \(\lambda = 1\), which is size 2, so \(\lambda_1=2\).
- Thus \begin{align*} \min_A(t) = (t-2)(t-1)^2 .\end{align*}
Fall 2020 #5
Consider the following matrix: \begin{align*} B \coloneqq \begin{bmatrix} 1 & 3 & 3 \\ 2 & 2 & 3 \\ -1 & -2 & -2 \end{bmatrix} .\end{align*}
-
Find the minimal polynomial of \(B\).
-
Find a \(3\times 3\) matrix \(J\) in Jordan canonical form such that \(B = JPJ^{-1}\) where \(P\) is an invertible matrix.
Extra Problems
Tons of extra fundamental problems here: https://math.ucr.edu/~mpierce/teaching/qual-algebra/fun/groups/
(DZG): these are just random extra problems that I found and dropped in. There is likely a ton of overlap/redundancy!
Linear Algebra
- For a division ring \(D\), let \(V_{i}\) be a finite dimensional vector space over \(D\) for \(i \in\{1, \ldots, k\}\). Suppose the sequence \begin{align*} 0 \longrightarrow V_{1} \longrightarrow V_{2} \longrightarrow \cdots V_{k} \longrightarrow 0 \end{align*} is exact. Prove that \(\sum_{i=1}^{k}(-1)^{i} \operatorname{dim}_{D} V_{i}=0\).
- Prove that if \(A\) and \(B\) are invertible matrices over a field \(\boldsymbol{k}\), then \(A+\lambda B\) is invertible for all but finitely many \(\lambda \in \boldsymbol{k}\).
- For the ring of \(n \times n\) matrices over a commutative unital ring \(R\), which we’ll denote \(\operatorname{Mat}_{n}(R)\), recall the definition of the determinant map det: \(\operatorname{Mat}_{n}(R) \rightarrow R\). For \(A \in \operatorname{Mat}_{n}(R)\) also recall the definition of the classical adjoint \(A^{a}\) of \(A\). Prove that:
- \(\operatorname{det}\left(A^{a}\right)=\operatorname{det}(A)^{n-1}\)
- \(\left(A^{a}\right)^{a}=\operatorname{det}(A)^{n-2} A\)
- If \(R\) is an integral domain and \(A\) is an \(n \times n\) matrix over \(R\), prove that if a system of linear equations \(A x=0\) has a nonzero solution then \(\operatorname{det} A=0\). Is the converse true? What if we drop the assumption that \(R\) is an integral domain?
- What is the companion matrix \(M\) of the polynomial \(f=x^{2}-x+2\) over \(C\) ? Prove that \(f\) is the minimal polynomial of \(M\).
- Suppose that \(\phi\) and \(\psi\) are commuting endomorphisms of a finite dimensional vector space \(E\) over a field \(\boldsymbol{k}\), so \(\phi \psi=\psi \phi\).
- Prove that if \(k\) is algebraically closed, then \(\phi\) and \(\psi\) have a common eigenvector.
- Prove that if \(E\) has a basis consisting of eigenvectors of \(\phi\) and \(E\) has a basis consisting of eigenvectors of \(\psi\), then \(E\) has a basis consisting of vectors that are eigenvectors for both \(\phi\) and \(\psi\) simultaneously.
Galois Theory
Taken from here: https://math.ucr.edu/~mpierce/teaching/qual-algebra/fun/galois/
- Suppose that for an extension field \(F\) over \(K\) and for \(a \in F\), we have that \(b \in F\) is algebraic over \(K(a)\) but transcendental over \(K\). Prove that \(a\) is algebraic over \(K(b)\).
- Suppose that for a field \(F / K\) that \(a \in F\) is algebraic and has odd degree over \(K\). Prove that \(a^{2}\) is also algebraic and has odd degree over \(K\), and furthermore that \(K(a)=K\left(a^{2}\right)\)
- For a polynomial \(f \in K[x]\), prove that if \(r \in F\) is a root of \(f\) then for any \(\sigma \in \mathbf{A u t}_{K} F, \sigma(r)\) is also a root of \(f\)
- Prove that as extensions of \(\boldsymbol{Q}, \boldsymbol{Q}(x)\) is Galois over \(\boldsymbol{Q}\left(x^{2}\right)\) but not over \(\boldsymbol{Q}\left(x^{3}\right)\).
- If \(F\) is over \(E\), and \(E\) is \(\quad\) over \(K\) is \(F\) necessarily over \(K\) ? Answer this question for each of the words “algebraic,” “normal,” and “separable” in the blanks.
- If \(F\) is over \(K\), and \(E\) is an intermediate extension of \(F\) over \(K\), is \(F\) necessarily over \(E ?\) Answer this question for each of the words “algebraic,” “normal,” and “separable” in the blanks.
- If \(F\) is some (not necessarily Galois) field extension over \(K\) such that \([F: K]=6\) and Aut \(_{K} F \simeq S_{3}\), then \(F\) is the splitting field of an irreducible cubic over \(K[x]\).
- Recall the definition of the join of two subgroups \(H \vee G\) (or \(H+G\) ). For \(F\) a finite dimensional Galois extension over \(K\) and let \(A\) and \(B\) be intermediate extensions. Prove that
- \(\operatorname{Aut}_{A B} F=\mathrm{Aut}_{A} F \cap \mathrm{Aut}_{B} F\)
- Aut \(_{A \cap B} F=\mathrm{Aut}_{A} F \vee \mathrm{Aut}_{B} F\)
- For a field \(K\) take \(f \in K[x]\) and let \(n=\operatorname{deg} f\). Prove that for a splitting field \(F\) of \(f\) over \(K\) that \([F: K] \leq n !\). Furthermore prove that \([F: K]\) divides \(n !\).
- Let \(F\) be the splitting field of \(f \in K[x]\) over \(K\). Prove that if \(g \in K[x]\) is irreducible and has a root in \(F\), then \(g\) splits into linear factors over \(F\).
- Prove that a finite field cannot be algebraically closed.
- For \(u=\sqrt{2+\sqrt{2}}\), What is the Galois group of \(\boldsymbol{Q}(u)\) over \(\boldsymbol{Q} ?\) What are the intermediate fields of the extension \(\boldsymbol{Q}(u)\) over \(\boldsymbol{Q}\) ?
- Characterize the splitting field and all intermediate fields of the polynomial \(\left(x^{2}-2\right)\left(x^{2}-3\right)\left(x^{2}-5\right)\) over \(Q\). Using this characterization, find a primitive element of the splitting field.
- Characterize the splitting field and all intermediate fields of the polynomial \(x^{4}-3\) over \(Q\)
- Consider the polynomial \(f=x^{3}-x+1\) in \(\boldsymbol{F}_{3}[x]\). Prove that \(f\) is irreducible. Calculate the degree of the splitting field of \(f\) over \(\boldsymbol{F}_{3}\) and the cardinality of the splitting field of \(f\).
- Given an example of a finite extension of fields that has infinitely many intermediate fields.
- Let \(u=\sqrt{3+\sqrt{2}}\). Is \(\boldsymbol{Q}(u)\) a splitting field of \(u\) over \(\boldsymbol{Q}\) ? (MathSE)
- Prove that the multiplicative group of units of a finite field must be cyclic, and so is generated by a single element.
- Prove that \(\boldsymbol{F}_{p^{n}}\) is the splitting field of \(x^{p^{n}}-x\) over \(\boldsymbol{F}_{p}\).
- Prove that for any positive integer \(n\) there is an irreducible polynomial of degree \(n\) over \(\boldsymbol{F}_{p}\)
- Recall the definition of a perfect field. Give an example of an imperfect field, and the prove that every finite field is perfect.
- For \(n>2\) let \(\zeta_{n}\) denote a primitive \(n\) th root of unity over \(Q\). Prove that \begin{align*} \left[\boldsymbol{Q}\left(\zeta_{n}+\zeta_{n}^{-1}: \boldsymbol{Q}\right)\right]=\frac{1}{2} \varphi(n) \end{align*} where \(\varphi\) is Euler’s totient function.
- Suppose that a field \(K\) with characteristic not equal to 2 contains an primitive \(n\) th root of unity for some odd integer \(n\). Prove that \(K\) must also contain a primitive \(2 n\) th root of unity.
- Prove that the Galois group of the polynomial \(x^{n}-1\) over \(Q\) is abelian.
Commutative Algebra
-
Show that a finitely generated module over a Noetherian local ring is flat iff it is free using Nakayama and Tor.
-
Show that \(\left\langle{ 2, x }\right\rangle{~\trianglelefteq~}{\mathbf{Z}}[x]\) is not a principal ideal.
-
Let \(R\) be a Noetherian ring and \(A,B\) algebras over \(R\). Suppose \(A\) is finite type over \(R\) and finite over B. Then \(B\) is finite type over \(R\).
Group Theory
Centralizing and Normalizing
-
Show that \(C_G(H) \subseteq N_G(H) \leq G\).
-
Show that \(Z(G) \subseteq C_G(H) \subseteq N_G(H)\).
-
Given \(H\subseteq G\), let \(S(H)= \bigcup_{g\in G} gHg^{-1}\), so \({\left\lvert {S(H)} \right\rvert}\) is the number of conjugates to \(H\). Show that \({\left\lvert {S(H)} \right\rvert} = [G : N_G(H)]\).
- That is, the number of subgroups conjugate to \(H\) equals the index of the normalizer of \(H\).
-
Show that \(Z(G) = \bigcap_{a\in G} C_G(a)\).
-
Show that the centralizer \(G_G(H)\) of a subgroup is again a subgroup.
-
Show that \(C_G(H) {~\trianglelefteq~}N_G(H)\) is a normal subgroup.
-
Show that \(C_G(G) = Z(G)\).
-
Show that for \(H\leq G\), \(C_H(x) = H \cap C_G(x)\).
-
Let \(H, K \leq G\) a finite group, and without using the normalizers of \(H\) or \(K\), show that \({\left\lvert {HK} \right\rvert} = {\left\lvert {H} \right\rvert} {\left\lvert {K} \right\rvert}/{\left\lvert {H\cap K} \right\rvert}\).
-
Show that if \(H \leq N_G(K)\) then \(HK \leq H\), and give a counterexample showing that this condition is necessary.
-
Show that \(HK\) is a subgroup of \(G\) iff \(HK = KH\).
-
Prove that the kernel of a homomorphism is a normal subgroup.
Primes in Group Theory
-
Show that any group of prime order is cyclic and simple.
-
Analyze groups of order \(pq\) with \(q<p\).
Hint: consider the cases when \(p\) does or does not divide \(q-1\).
- Show that if \(q\) does not divide \(p-1\), then \(G\) is cyclic.
- Show that \(G\) is never simple.
-
Analyze groups of order \(p^2 q\).
Hint: Consider the cases when \(q\) does or does not divide \(p^2 - 1\).
-
Show that no group of order \(p^2 q^2\) is simple for \(p<q\) primes.
-
Show that a group of order \(p^2 q^2\) has a normal Sylow subgroup.
-
Show that a group of order \(p^2 q^2\) where \(q\) does not divide \(p^2-1\) and \(p\) does not divide \(q^2-1\) is abelian.
-
Show that every group of order \(pqr\) with \(p<q<r\) primes contains a normal Sylow subgroup.
- Show that \(G\) is never simple.
-
Let \(p\) be a prime and \({\left\lvert {G} \right\rvert} = p^3\). Prove that \(G\) has a normal subgroup \(N\) of order \(p^2\).
-
Suppose \(N = \left\langle{h}\right\rangle\) is cyclic and classify all possibilities for \(G\) if:
- \({\left\lvert {h} \right\rvert} = p^3\)
- \({\left\lvert {h} \right\rvert} = p\).
Hint: Sylow and semidirect products.
-
-
Show that any normal \(p{\hbox{-}}\) subgroup is contained in every Sylow \(p{\hbox{-}}\)subgroup of \(G\).
-
Show that the order of \(1+p\) in \(\qty{{\mathbf{Z}}/p^2{\mathbf{Z}}}^{\times}\) is equal to \(p\). Use this to construct a non-abelian group of order \(p^3\).
p-Groups
-
Show that every \(p{\hbox{-}}\)group has a nontrivial center.
-
Show that every \(p{\hbox{-}}\)group is nilpotent.
-
Show that every \(p{\hbox{-}}\)group is solvable.
-
Show that every maximal subgroup of a \(p{\hbox{-}}\)group has index \(p\).
-
Show that every maximal subgroup of a \(p{\hbox{-}}\)group is normal.
-
Show that every group of order \(p\) is cyclic.
-
Show that every group of order \(p^2\) is abelian and classify them.
-
Show that every normal subgroup of a \(p{\hbox{-}}\)group is contained in the center.
Hint: Consider \(G/Z(G)\).
-
Let \(O_P(G)\) be the intersection of all Sylow \(p{\hbox{-}}\)subgroups of \(G\). Show that \(O_p(G) {~\trianglelefteq~}G\), is maximal among all normal \(p{\hbox{-}}\)subgroups of \(G\)
-
Let \(P\in {\operatorname{Syl}}_p(H)\) where \(H{~\trianglelefteq~}G\) and show that \(P\cap H \in {\operatorname{Syl}}_p(H)\).
-
Show that Sylow \(p_i{\hbox{-}}\)subgroups \(S_{p_1}, S_{p_2}\) for distinct primes \(p_1\neq p_2\) intersect trivially.
-
Show that in a \(p\) group, every normal subgroup intersects the center nontrivially.
Symmetric Groups
Specific Groups
- Show that the center of \(S_3\) is trivial.
- Show that \(Z(S_n) = 1\) for \(n\geq 3\)
- Show that \(\mathop{\mathrm{Aut}}(S_3) = \mathop{\mathrm{Inn}}(S_3) \cong S_3\).
- Show that the transitive subgroups of \(S_3\) are \(S_3, A_3\)
- Show that the transitive subgroups of \(S_4\) are \(S_4, A_4, D_4, {\mathbf{Z}}_2^2, {\mathbf{Z}}_4\).
- Show that \(S_4\) has two normal subgroups: \(A_4, {\mathbf{Z}}_2^2\).
- Show that \(S_{n\geq 5}\) has one normal subgroup: \(A_n\).
- \(Z(A_n) = 1\) for \(n\geq 4\)
- Show that \([S_n, S_n] = A_n\)
- Show that \([A_4, A_4] \cong {\mathbf{Z}}_2^2\)
- Show that \([A_n, A_n] = A_n\) for \(n\geq 5\), so \(A_{n\geq 5}\) is nonabelian.
General Structure
- Show that an \(m{\hbox{-}}\)cycle is an odd permutation iff \(m\) is an even number.
- Show that a permutation is odd iff it has an odd number of even cycles.
- Show that the center of \(S_n\) for \(n\geq 4\) is nontrivial.
- Show that disjoint cycles commute.
- Show directly that any \(k{\hbox{-}}\)cycle is a product of transpositions, and determine how many transpositions are needed.
Generating Sets
-
Show that \(S_n\) is generated by any of the following types of cycles:
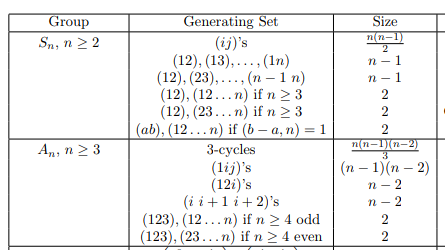
- Show that \(S_n\) is generated by transpositions.
- Show that \(S_n\) is generated by adjacent transpositions.
- Show that \(S_n\) is generated by \(\left\{{(12), (12\cdots n)}\right\}\) for \(n\geq 2\)
- Show that \(S_n\) is generated by \(\left\{{(12), (23\cdots n)}\right\}\) for \(n\geq 3\)
- Show that \(S_n\) is generated by \(\left\{{(ab), (12\cdots n)}\right\}\) where \(1\leq a<b\leq n\) iff \(\gcd(b-a, n) = 1\).
- Show that \(S_p\) is generated by any arbitrary transposition and any arbitrary \(p{\hbox{-}}\)cycle.
Alternating Groups
- Show that \(A_n\) is generated \(3{\hbox{-}}\)cycles.
- Prove that \(A_n\) is normal in \(S_n\).
- Argue that \(A_n\) is simple for \(n \geq 5\).
- Show that \(\mathop{\mathrm{Out}}(A_4)\) is nontrivial.
Dihedral Groups
- Show that if \(N{~\trianglelefteq~}D_n\) is a normal subgroup of a dihedral group, then \(D_n/N\) is again a dihedral group.
Other Groups
- Show that \({\mathbf{Q}}\) is not finitely generated as a group.
- Show that the Quaternion group has only one element of order 2, namely \(-1\).
Classification
-
Show that no group of order 36 is simple.
-
Show that no group of order 90 is simple.
-
Classifying all groups of order 99.
-
Show that all groups of order 45 are abelian.
-
Classify all groups of order 10.
-
Classify the five groups of order 12.
-
Classify the four groups of order 28.
-
Show that if \({\left\lvert {G} \right\rvert} = 12\) and has a normal subgroup of order 4, then \(G \cong A_4\).
-
Suppose \({\left\lvert {G} \right\rvert} = 240 = s^4 \cdot 3 \cdot 5\).
- How many Sylow-\(p\) subgroups does \(G\) have for \(p\in \left\{{2, 3, 5}\right\}\)?
- Show that if \(G\) has a subgroup of order 15, it has an element of order 15.
- Show that if \(G\) does not have such a subgroup, the number of Sylow-\(3\) subgroups is either 10 or 40.
Hint: Sylow on the subgroup of order 15 and semidirect products.
Group Actions
- Show that the stabilizer of an element \(G_x\) is a subgroup of \(G\).
- Show that if \(x, y\) are in the same orbit, then their stabilizers are conjugate.
- Show that the stabilizer of an element need not be a normal subgroup?
- Show that if \(G \curvearrowright X\) is a group action, then the stabilizer \(G_x\) of a point is a subgroup.
Series of Groups
-
Show that \(A_n\) is simple for \(n\geq 5\)
-
Give a necessary and sufficient condition for a cyclic group to be solvable.
-
Prove that every simple abelian group is cyclic.
-
Show that \(S_n\) is generated by disjoint cycles.
-
Show that \(S_n\) is generated by transpositions.
-
Show if \(G\) is finite, then \(G\) is solvable \(\iff\) all of its composition factors are of prime order.
-
Show that if \(N\) and \(G/N\) are solvable, then \(G\) is solvable.
-
Show that if \(G\) is finite and solvable then every composition factor has prime order.
-
Show that \(G\) is solvable iff its derived series terminates.
-
Show that \(S_3\) is not nilpotent.
-
Show that \(G\) nilpotent \(\implies G\) solvable
-
Show that nilpotent groups have nontrivial centers.
-
Show that Abelian \(\implies\) nilpotent
-
Show that p-groups \(\implies\) nilpotent
Misc
-
Prove Burnside’s theorem.
-
Show that \(\mathop{\mathrm{Inn}}(G) {~\trianglelefteq~}Aut(G)\)
-
Show that \(\mathop{\mathrm{Inn}}(G) \cong G / Z(G)\)
-
Show that the kernel of the map \(G\to \mathop{\mathrm{Aut}}(G)\) given by \(g\mapsto (h\mapsto ghg^{-1})\) is \(Z(G)\).
-
Show that \(N_G(H) / C_G(H) \cong A \leq Aut(H)\)
-
Give an example showing that normality is not transitive: i.e. \(H{~\trianglelefteq~}K {~\trianglelefteq~}G\) with \(H\) not normal in \(G\).
Nonstandard Topics
-
Show that \(H~\text{char}~G \Rightarrow H \unlhd G\)
Thus “characteristic” is a strictly stronger condition than normality
-
Show that \(H ~\text{char}~ K ~\text{char}~G \Rightarrow H ~\text{char}~ G\)
So “characteristic” is a transitive relation for subgroups.
-
Show that if \(H \leq G\), \(K{~\trianglelefteq~}G\) is a normal subgroup, and \(H~\text{char}~K\) then \(H\) is normal in \(G\).
So normality is not transitive, but strengthening one to “characteristic” gives a weak form of transitivity.
Ring Theory
Basic Structure
- Show that if an ideal \(I{~\trianglelefteq~}R\) contains a unit then \(I = R\).
- Show that \(R^{\times}\) need not be closed under addition.
Ideals
- \(\star\) Show that if \(x\) is not a unit, then \(x\) is contained in some maximal ideal.
Every \(a\in R\) for a finite ring is either a unit or a zero divisor.
\hfill
- Let \(a\in R\) and define \(\phi(x) = ax\).
- If \(\phi\) is injective, then it is surjective, so \(1 = ax\) for some \(x \implies x^{-1}= a\).
- Otherwise, \(ax_1 = ax_2\) with \(x_1 \neq x_2 \implies a(x_1 - x_2) = 0\) and \(x_1 - x_2 \neq 0\)
- So \(a\) is a zero divisor.
Maximal \(\implies\) prime, but generally not the converse.
-
Suppose \({\mathfrak{m}}\) is maximal, \(ab\in {\mathfrak{m}}\), and \(b\not\in {\mathfrak{m}}\).
-
Then there is a containment of ideals \({\mathfrak{m}}\subsetneq {\mathfrak{m}}+ (b) \implies {\mathfrak{m}}+ (b) = R\).
-
So \begin{align*} 1 = m + rb \implies a = am + r(ab) ,\end{align*} but \(am\in {\mathfrak{m}}\) and \(ab\in {\mathfrak{m}}\implies a\in {\mathfrak{m}}\).
Counterexample: \((0) \in {\mathbf{Z}}\) is prime since \({\mathbf{Z}}\) is a domain, but not maximal since it is properly contained in any other ideal.
- Show that every proper ideal is contained in a maximal ideal
- Show that if \(x\in R\) a PID, then \(x\) is irreducible \(\iff \left\langle{x}\right\rangle{~\trianglelefteq~}R\) is maximal.
- Show that intersections, products, and sums of ideals are ideals.
- Show that the union of two ideals need not be an ideal.
- Show that every ring has a proper maximal ideal.
- Show that \(I{~\trianglelefteq~}R\) is maximal iff \(R/I\) is a field.
- Show that \(I {~\trianglelefteq~}R\) is prime iff \(R/I\) is an integral domain.
- Show that \(\cup_{{\mathfrak{m}}\in {\operatorname{maxSpec}}(R)} = R\setminus R^{\times}\).
- Show that \({\operatorname{maxSpec}}(R) \subsetneq \operatorname{Spec}(R)\) but the containment is strict.
- Show that every prime ideal is radical.
- Show that the nilradical is given by \({\sqrt{0_{R}} } = \sqrt{(}0)\).
- Show that \(\text{rad}(IJ) = \text{rad}(I) \cap\text{rad}(J)\)
- Show that if \(\operatorname{Spec}(R) \subseteq {\operatorname{maxSpec}}(R)\) then \(R\) is a UFD.
- Show that if \(R\) is Noetherian then every ideal is finitely generated.
Characterizing Certain Ideals
- Show that for an ideal \(I{~\trianglelefteq~}R\), its radical is the intersection of all prime ideals containing \(I\).
- Show that \(\sqrt{I}\) is the intersection of all prime ideals containing \(I\).
The nilradical is contained in the Jacobson radical, i.e. \begin{align*} {\sqrt{0_{R}} } \subseteq J(R) .\end{align*}
Maximal \(\implies\) prime, and so if \(x\) is in every prime ideal, it is necessarily in every maximal ideal as well.
\(R/ {\sqrt{0_{R}} }\) has no nonzero nilpotent elements.
\begin{align*} a + {\sqrt{0_{R}} } \text{ nilpotent } &\implies (a+ {\sqrt{0_{R}} })^n \coloneqq a^n + {\sqrt{0_{R}} }= {\sqrt{0_{R}} } \\ &\implies a^n \in {\sqrt{0_{R}} } \\ &\implies \exists \ell \text{ such that } (a^n)^\ell = 0 \\ &\implies a\in {\sqrt{0_{R}} } . \end{align*}
The nilradical is the intersection of all prime ideals, i.e. \begin{align*} {\sqrt{0_{R}} } = \bigcap_{\mathfrak{p} \in \operatorname{Spec}(R)} \mathfrak{p} \end{align*}
-
\({\sqrt{0_{R}} } \subseteq \cap\mathfrak{p}\):
-
\(x \in {\sqrt{0_{R}} } \implies x^n = 0 \in \mathfrak p \implies x\in \mathfrak{p} \text{ or } x^{n-1}\in\mathfrak p\).
-
\(R\setminus{\sqrt{0_{R}} } \subseteq \cup_{{\mathfrak{p}}} (R\setminus\mathfrak{p})\):
-
Define \(S = \left\{{I{~\trianglelefteq~}R {~\mathrel{\Big\vert}~}a^n\not\in I \text{ for any } n}\right\}\).
-
Then apply Zorn’s lemma to get a maximal ideal \({\mathfrak{m}}\), and maximal \(\implies\) prime.
Misc
- Show that localizing a ring at a prime ideal produces a local ring.
- Show that \(R\) is a local ring iff for every \(x\in R\), either \(x\) or \(1-x\) is a unit.
- Show that if \(R\) is a local ring then \(R\setminus R^{\times}\) is a proper ideal that is contained in the Jacobson radical \(J(R)\).
- Show that if \(R\neq 0\) is a ring in which every non-unit is nilpotent then \(R\) is local.
- Show that every prime ideal is primary.
- Show that every prime ideal is irreducible.
Field Theory
General Algebra
- Show that any finite integral domain is a field.
- Show that every field is simple.
- Show that any field morphism is either 0 or injective.
- Show that if \(L/F\) and \(\alpha\) is algebraic over both \(F\) and \(L\), then the minimal polynomial of \(\alpha\) over \(L\) divides the minimal polynomial over \(F\).
- Prove that if \(R\) is an integral domain, then \(R[t]\) is again an integral domain.
- Show that \(ff(R[t]) = ff(R)(t)\).
-
Show that \([{\mathbf{Q}}(\sqrt 2 + \sqrt 3) : {\mathbf{Q}}] = 4\).
- Show that \({\mathbf{Q}}(\sqrt 2 + \sqrt 3) = {\mathbf{Q}}(\sqrt 2 - \sqrt 3) = {\mathbf{Q}}(\sqrt 2, \sqrt 3)\).
- Show that the splitting field of \(f(x) = x^3-2\) is \({\mathbf{Q}}(\sqrt[3]{2}, \zeta_2)\).
Extensions?
- What is \([{\mathbf{Q}}(\sqrt 2 + \sqrt 3): {\mathbf{Q}}]\)?
- What is \([{\mathbf{Q}}(2^{3\over 2}) : {\mathbf{Q}}]\)?
- Show that if \(p\in {\mathbf{Q}}[x]\) and \(r\in {\mathbf{Q}}\) is a rational root, then in fact \(r\in {\mathbf{Z}}\).
- If \(\left\{{\alpha_i}\right\}_{i=1}^n \subset F\) are algebraic over \(K\), show that \(K[\alpha_1, \cdots, \alpha_n] = K(\alpha_1, \cdots, \alpha_n)\).
- Show that \(\alpha/F\) is algebraic \(\iff F(\alpha)/F\) is a finite extension.
- Show that every finite field extension is algebraic.
- Show that if \(\alpha, \beta\) are algebraic over \(F\), then \(\alpha\pm \beta, \alpha\beta^{\pm 1}\) are all algebraic over \(F\).
- Show that if \(L/K/F\) with \(K/F\) algebraic and \(L/K\) algebraic then \(L\) is algebraic.
Special Polynomials
- Show that a field with \(p^n\) elements has exactly one subfield of size \(p^d\) for every \(d\) dividing \(n\).
- Show that \(x^{p^n} - x = \prod f_i(x)\) over all irreducible monic \(f_i\) of degree \(d\) dividing \(n\).
- Show that \(x^{p^d} - x \divides x^{p^n} - x \iff d \divides n\)
- Prove that \(x^{p^n}-x\) is the product of all monic irreducible polynomials in \({ \mathbf{F} }_p[x]\) with degree dividing \(n\).
- Prove that an irreducible \(\pi(x)\in { \mathbf{F} }_p[x]\) divides \(x^{p^n}-x \iff \deg \pi(x)\) divides \(n\).
Galois Theory
Theory
- Show that if \(K/F\) is the splitting field of a separable polynomial then it is Galois.
- Show that any quadratic extension of a field \(F\) with \(\operatorname{ch}(F)\neq 2\) is Galois.
-
Show that if \(K/E/F\) with \(K/F\) Galois then \(K/E\) is always Galois with \(g(K/E) \leq g(K/F)\).
- Show additionally \(E/F\) is Galois \(\iff g(K/E) {~\trianglelefteq~}g(K/F)\).
- Show that in this case, \(g(E/F) = g(K/F) / g(K/E)\).
- Show that if \(E/k, F/k\) are Galois with \(E\cap F = k\), then \(EF/k\) is Galois and \(G(EF/k) \cong G(E/k)\times G(F/k)\).
Computations
- Show that the Galois group of \(x^n - 2\) is \(D_n\), the dihedral group on \(n\) vertices.
- Compute all intermediate field extensions of \({\mathbf{Q}}(\sqrt 2, \sqrt 3)\), show it is equal to \({\mathbf{Q}}(\sqrt 2 + \sqrt 3)\), and find a corresponding minimal polynomial.
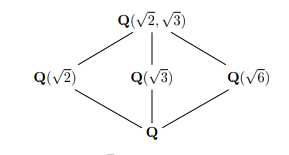
- Compute all intermediate field extensions of \({\mathbf{Q}}(2^{1\over 4}, \zeta_8)\).
- Show that \({\mathbf{Q}}(2^{1\over 3})\) and \({\mathbf{Q}}(\zeta_3 2^{1\over 3})\)
- Show that if \(L/K\) is separable, then \(L\) is normal \(\iff\) there exists a polynomial \(p(x) = \prod_{i=1}^n x- \alpha_i\in K[x]\) such that \(L = K(\alpha_1, \cdots, \alpha_n)\) (so \(L\) is the splitting field of \(p\)).
- Is \({\mathbf{Q}}(2^{1\over 3})/{\mathbf{Q}}\) normal?
- Show that \({\mathbf{GF}}(p^n)\) is the splitting field of \(x^{p^n} - x \in { \mathbf{F} }_p[x]\).
- Show that \({\mathbf{GF}}(p^d) \leq {\mathbf{GF}}(p^n) \iff d\divides n\)
- Compute the Galois group of \(x^n - 1 \in {\mathbf{Q}}[x]\) as a function of \(n\).
- Identify all of the elements of the Galois group of \(x^p-2\) for \(p\) an odd prime (note: this has a complicated presentation).
- Show that \({ \operatorname{Gal}}(x^{15}+2)/{\mathbf{Q}}\cong S_2 \rtimes{\mathbf{Z}}/15{\mathbf{Z}}\) for \(S_2\) a Sylow \(2{\hbox{-}}\)subgroup.
- Show that \({ \operatorname{Gal}}(x^3+4x+2)/{\mathbf{Q}}\cong S_3\), a symmetric group.
Modules and Linear Algebra
- Prove the Cayley-Hamilton theorem.
- Prove that the minimal polynomial divides the characteristic polynomial.
- Prove that the cokernel of \(A\in \operatorname{Mat}(n\times n, {\mathbf{Z}})\) is finite \(\iff \operatorname{det}A \neq 0\), and show that in this case \({\left\lvert {\operatorname{coker}(A)} \right\rvert} = {\left\lvert {\operatorname{det}(A)} \right\rvert}\).
- Show that a nilpotent operator is diagonalizable.
- Show that if \(A,B\) are diagonalizable and \([A, B] = 0\) then \(A,B\) are simultaneously diagonalizable.
- Does diagonalizable imply invertible? The converse?
- Does diagonalizable imply distinct eigenvalues?
- Show that if a matrix is diagonalizable, its minimal polynomial is squarefree.
- Show that a matrix representing a linear map \(T:V\to V\) is diagonalizable iff \(V\) is a direct sum of eigenspaces \(V = \bigoplus_i \ker(T -\lambda_i I)\).
- Show that if \(\left\{{\mathbf{v}_i}\right\}\) is a basis for \(V\) where \(\dim(V) = n\) and \(T(\mathbf{v}_i) = \mathbf{v}_{i+1 \operatorname{mod}n}\) then \(T\) is diagonalizable with minimal polynomial \(x^n-1\).
- Show that if the minimal polynomial of a linear map \(T\) is irreducible, then every \(T{\hbox{-}}\)invariant subspace has a \(T{\hbox{-}}\)invariant complement.
Linear Algebra
\todo[inline]{Sort out from module section.}
Even More Algebra Questions
(DZG): These all come from a random PDF I found, but I couldn’t find the original author/source!
Groups
Question 1.1
What is a normal subgroup? Can you get some natural map from a normal subgroup? What topological objects can the original group, normal subgroup, and quotient group relate to?
Question 1.2
Prove that a subgroup of index two is normal.
Question 1.3
Find all normal subgroups of \(A_4\).
Question 1.4
Give an interesting example of a non-normal subgroup. Is \({\operatorname{SO}}(2)\) normal inside \(SL_2(R)\)?
Question 1.5
Is normality transitive? That is, is a normal subgroup of a normal subgroup normal in the biggest group?
Question 1.6.
Define a solvable group. Give an example of a solvable nonabelian group.
Show \(A_4\) is solvable. Do the Sylow theorems tell you anything about whether this index 3 subgroup of \(A_4\) is normal?
Question 1.7
Define lower central series, upper central series, nilpotent and solvable groups.
Question 1.8
Define the derived series. Define the commutator. State and prove two nontrivial theorems about derived series.
Question 1.9
Prove that \(SL_2(Z)\) is not solvable.
Question 1.10
What are all possible orders of elements of \({\operatorname{SL}}_2(Z)\)?
Question 1.11
Can you show that all groups of order \(p^n\) for \(p\) prime are solvable? Do you know how to do this for groups of order \(p^r q^s\)?
Question 1.12
Suppose a \(p{\hbox{-}}\)group acts on a set whose cardinality is not divisible by \(p\) (\(p\) prime). Prove that there is a fixed point for the action.
Question 1.13
Prove that the centre of a group of order \(pr\) (\(p\) prime) is not trivial.
Question 1.14
Give examples of simple groups. Are there infinitely many?
Question 1.15
State and prove the Jordan-Holder theorem for finite groups.
Question 1.16
What’s Cayley’s theorem? Give an example of a group of order \(n\) that embeds in \(S_m\) for some \(m\) smaller than \(n\).
Give an example of a group where you have to use \(S_n\).
Question 1.17
Is \(A_4\) a simple group? What are the conjugacy classes in \(S_4\)? What about in \(A_4\)?
Question 1.18
Talk about conjugacy classes in the symmetric group \(S_n\).
Question 1.19
When do conjugacy classes in \(S_n\) split in \(A_n\)?
Question 1.20
What is the centre of \(S_n\)? Prove it.
Question 1.21
Prove that the alternating group \(A_n\) is simple for \(n \geq 5\).
Question 1.22
Prove the alternating group on \(n\) letters is generated by the 3-cycles for \(n \geq 3\).
Question 1.23
Prove that for \(p\) prime, Sp is generated by a \(p{\hbox{-}}\)cycle and a transposition.
Question 1.24
What is the symmetry group of a tetrahedron? Cube? Icosahedron?
Question 1.25
How many ways can you color the tetrahedron with C colors if we identify symmetric colorings?
Question 1.26.
What is the symmetry group of an icosahedron? What’s the stabiliser of an edge?
How many edges are there? How do you know the symmetry group of the icosahedron is the same as the symmetry group of the dodecahedron?
Do you know the classification of higher-dimensional polyhedra?
Question 1.27
Do you know what the quaternion group is? How many elements are there of each order?
Question 1.28
What is the group of unit quaternions topologically? What does it have to do with \({\operatorname{SO}}(3)\)?
Question 1.29
What’s the stabiliser of a point in the unit disk under the group of conformal automorphisms?
Question 1.30
What group-theoretic construct relates the stabiliser of two points?
Question 1.31
Consider \({\operatorname{SL}}_2(R)\) acting on \({\mathbf{R}}^2\) by matrix multiplication. What is the stabiliser of a point? Does it depend which point? Do you know what sort of subgroup this is? What if \({\operatorname{SL}}_2(R)\) acts by Möbius transformations instead?
Question 1.32
What are the polynomials in two real variables that are invariant under the action of \(D_4\), the symmetry group of a square, by rotations and reflections on the plane that the two variables form?
Question 1.33
Give an interesting example of a subgroup of the additive group of the rationals.
Question 1.34
Talk about the isomorphism classes of subgroups of \({\mathbf{Q}}\). How many are there? Are the ones you’ve given involving denominators divisible only by certain primes distinct? So that gives you the cardinality. Are these all of them?
Question 1.35
Is the additive group of the reals isomorphic to the multiplicative group of the positive reals? Is the same result true with reals replaced by rationals?
Question 1.36
What groups have nontrivial automorphisms?
Question 1.37
A subgroup \(H\) of a group \(G\) that meets every conjugacy class is in fact \(G\). Why is that true?
Question 1.38
Let \(G\) be the group of invertible \(3\times 3\) matrices over \({ \mathbf{F} }_p\), for \(p\) prime. What does basic group theory tell us about \(G\)?
How many conjugates does a Sylow \(p{\hbox{-}}\)subgroup have? Give a matrix form for the elements in this subgroup.
Explain the conjugacy in terms of eigenvalues and eigenvectors. give a matrix form for the normaliser of the Sylow \(p{\hbox{-}}\)subgroup.
Question 1.39
Let’s look at \({\operatorname{SL}}_2({ \mathbf{F} }_3)\). How many elements are in that group? What is its centre? Identify \({\operatorname{PSL}}_2({ \mathbf{F} }_3)\) as a permutation group.
Question 1.40
How many elements does \({\mathfrak{gl}}_2({ \mathbf{F} }_q)\) have? How would you construct representations?
What can you say about the 1-dimensional representations? What can you say about simplicity of some related groups?
Question 1.41.
A subgroup of a finitely-generated free abelian group is?
A subgroup of a finitely-generated free group is..? Prove your answers.
Question 1.42
What are the subgroups of \({\mathbf{Z}}^2\)?
Question 1.43
What are the subgroups of the free group \(F_2\)? How many generators can you have?
Can you find one with 3 generators? 4 generators? Countably many generators?
Is the subgroup with 4 generators you found normal? Why? Can you find a normal one?
Question 1.44
Talk about the possible subgroups of \({\mathbf{Z}}^3\). Now suppose that you have a subgroup of \({\mathbf{Z}}^3\). What theorem tells you something about the structure of the quotient group?
Classification of Finite groups
Question 2.1
Given a finite abelian group with at most n elements of order divisible by n, prove it’s cyclic.
Question 2.2
Suppose I asked you to classify groups of order 4. Why isn’t there anything else? Which of those could be realised as a Galois group over \({\mathbf{Q}}\)?
Question 2.3
State/prove the Sylow theorems.
Question 2.4
Classify groups of order 35.
Question 2.5
Classify groups of order 21.
Question 2.6
Discuss groups of order 55.
Question 2.7
Classify groups of order 14. Why is there a group of order 7? Are all index-2 subgroups normal?
Question 2.8
How many groups are there of order 15? Prove it.
Question 2.9
Classify all groups of order 8.
Question 2.10
Classify all groups of order \(p^3\) for \(p\) prime.
Question 2.11
What are the groups of order \(p^2\)? What about \(pq\)? What if \(q\) is congruent to \(1\operatorname{mod}p\)?
Question 2.12
What are the groups of order 12? Can there be a group of order 12 with 2 nonisomorphic subgroups of the same order?
Question 2.13
How would you start finding the groups of order 56? Is there in fact a way for \({\mathbf{Z}}/7{\mathbf{Z}}\) to act on a group of order 8 nontrivially?
Question 2.14
How many abelian groups are there of order 36?
Question 2.15
What are the abelian groups of order 16?
Question 2.16.
What are the abelian groups of order 9? Prove that they are not isomorphic. groups of order 27?
Question 2.17
How many abelian groups of order 200 are there?
Question 2.18
Prove there is no simple group of order 132.
Question 2.19
Prove that there is no simple group of order 160. What can you say about the structure of groups of that order?
Question 2.20
Prove that there is no simple group of order 40.
Fields and Galois Theory
Question 3.1
What is the Galois group of a finite field? What is a generator? How many elements does a finite field have? What can you say about the multiplicative group? Prove it.
Question 3.2
Classify finite fields, their subfields, and their field extensions. What are the automorphisms of a finite field?
Question 3.3
Take a finite field extension \({ \mathbf{F} }_p^n\) over \({ \mathbf{F} }_p\). What is Frobenius? What is its characteristic polynomial?
Question 3.4
What are the characteristic and minimal polynomial of the Frobenius automorphism?
Question 3.5
What’s the field with 25 elements?
Question 3.6
What is the multiplicative group of \({ \mathbf{F} }_9\)?
Question 3.7
What is a separable extension? Can \({\mathbf{Q}}\) have a non-separable extension? How about \({\mathbf{Z}}/p{\mathbf{Z}}\)? Why not? Are all extensions of characteristic 0 fields separable? Of finite fields? Prove it.
Give an example of a field extension that’s not separable.
Question 3.8
Are there separable polynomials of any degree over any field?
Question 3.9
What is a perfect field and why is this important? Give an example of a non-perfect field.
Question 3.10
What is Galois theory? State the main theorem. What is the splitting field of \(x^5 - 2\) over \({\mathbf{Q}}\)? What are the intermediate extensions? Which extensions are normal, which are not, and why? What are the Galois groups (over Q) of all intermediate extensions?
Question 3.11
What is a Galois extension?
Question 3.12
Take a quadratic extension of a field of characteristic 0. Is it Galois? Take a degree 2 extension on top of that. Does it have to be Galois over the base field? What statement in group theory can you think of that reflects this?
Question 3.13.
Is Abelian Galois extension transitive? That is, if \(K\) has abelian Galois group over \(E\), \(E\) has abelian Galois group over \(F\) , and \(K\) is a Galois extension of \(F\), is it necessarily true that \({ \mathsf{Gal}}(K/F)\) is also abelian? Give a counterexample involving number fields as well as one involving function fields.
Question 3.14
What is a Kummer extension?
Question 3.15
Say you have a field extension with only finitely many intermediate fields. Show that it is a simple extension.
Question 3.16
Tell me a condition on the Galois group which is implied by irreducibility of the polynomial. What happens when the polynomial has a root in the base field?
Question 3.17
What is the discriminant of a polynomial?
Question 3.18
If we think of the Galois group of a polynomial as contained in \(S_n\), when is it contained in \(A_n\)?
Question 3.19
Is \({\mathbf{Q}}(\sqrt[3]{21})\) normal? What is its splitting field? What is its Galois group? Draw the lattice of subfields.
Question 3.20
What’s the Galois group of \(x^2 + 1\) over Q? What’s the integral closure of \({\mathbf{Z}}\) in \({\mathbf{Q}}(i)\)?
Question 3.21
What’s the Galois group of \(x^2 + 9\)?
Question 3.22
What is the Galois group of \(x^2 - 2\)? Why is \(x^2 - 2\) irreducible?
Question 3.23
What is the Galois group of \begin{align*} {\mathbf{Q}}(\sqrt 2, \sqrt 3)\, / \, {\mathbf{Q}} ?\end{align*}
Question 3.24
What is the Galois group of \begin{align*} {\mathbf{Q}}\qty{ \sqrt{n_1}, \cdots, \sqrt{n_m} } \, / \, {\mathbf{Q}}(\sqrt{n_1} + \cdots + \sqrt{n_m}) ?\end{align*}
Question 3.25
What are the Galois groups of irreducible cubics?
Question 3.26
If an irreducible cubic polynomial has Galois group NOT contained in A3, does it necessarily have to be all of \(S_3\)?
Question 3.27
Compute the Galois group of \(x^3 - 2\) over the rationals.
Question 3.28
How would you find the Galois group of \(x^3 + 2x + 1\)? Adjoin a root to \({\mathbf{Q}}\). Can you say something about the roots of \(x^3 + 3x + 1\) in this extension?
Question 3.29
Compute the Galois group of \(x^3 + 6x + 3\).
Question 3.30
Find the Galois group of \(x^4 - 2\) over Q.
Question 3.31
What’s the Galois group of \(x^4 - 3\)?
Question 3.32
What is the Galois group of \(x^4 - 2x^2 + 9\)?
Question 3.33
Calculate the Galois group of \(x^5 - 2\).
Question 3.34.
Discuss sufficient conditions on a polynomial of degree 5 to have Galois group \(S_5\) over \({\mathbf{Q}}\) and prove your statements.
Question 3.35
Show that if \(f\) is an irreducible quintic with precisely two non-real roots, then its Galois group is \(S_5\).
Question 3.36
Suppose you have a degree 5 polynomial over a field. What are necessary and sufficient conditions for its Galois group to be of order divisible by 3? Can you give an example of an irreducible polynomial in which this is not the case?
Question 3.37
What is the Galois group of \(x^7 - 1\) over the rationals?
Question 3.38
What is the Galois group of the polynomial \(x^n - 1\) over \({\mathbf{Q}}\)?
Question 3.39
Describe the Galois theory of cyclotomic extensions.
Question 3.40
What is the maximal real field in a cyclotomic extension \({\mathbf{Q}}(\zeta_n)/{\mathbf{Q}}\)?
Question 3.41
Compute the Galois group of \(p(x) = x^7 - 3\).
Question 3.42
What Galois stuff can you say about \(x^{2n} - 2\)?
Question 3.43
What are the cyclic extensions of (prime) order \(p\)?
Question 3.44
Can you give me a polynomial whose Galois group is \({\mathbf{Z}}/3{\mathbf{Z}}\)?
Question 3.45
Which groups of order 4 can be realised as a Galois group over \({\mathbf{Q}}\)?
Question 3.46
Give a polynomial with \(S_3\) as its Galois group.
Question 3.47
Give an example of a cubic with Galois group \(S_3\).
Question 3.48
How do you construct a polynomial over \({\mathbf{Q}}\) whose Galois group is \(S_n\)? Do it for \(n = 7\) in particular.
Question 3.49
What’s a Galois group that’s not \(S_n\) or \(A_n\)?
Question 3.50
Which finite groups are Galois groups for some field extension?
Question 3.51
What Galois group would you expect a cubic to have?
Question 3.52
Draw the subgroup lattice for \(S_3\).
Question 3.53
Do you know what the quaternion group is? How many elements are there of each order? Suppose I have a field extension of the rationals with Galois group the quaternion group. How many quadratic extensions does it contain? Can any of them be imaginary?
Question 3.54
Suppose you are given a finite Galois extension \(K/{\mathbf{Q}}\) by \(f(x) \in {\mathbf{Z}}[x]\) such that \(\deg(f ) = n\) and \({ \mathsf{Gal}}(K/Q) = S_n\). What can you say about the roots?
Question 3.55
How many automorphisms does the complex field have? How can you extend a simple automorphism \(\sqrt{2} \mapsto -\sqrt{2}\) of an algebraic field into \({\mathbf{C}}\)? How can you extend a subfield automorphism? What feature of \({\mathbf{C}}\) allows you to?
Question 3.56.
Can it happen that a proper subfield of C is isomorphic to C? How?
Question 3.57
Consider the minimal polynomial \(f(x)\) for a primitive \(m\)th root of unity. Prove that if \(p\) divides \(f(a)\) for some integer \(a\) and \(\gcd(p, m) = 1\) then \(m\) divides \(p - 1\). Use this fact to show that there are infinitely many primes congruent to \(1 \operatorname{mod}m\).
Question 3.58
What is Dirichlet’s theorem about primes in arithmetic progression? What can you say about the density of such primes?
Question 3.59
How many irreducible polynomials of degree six are there over \({ \mathbf{F} }_2\)?
Question 3.60
Can you have a degree 7 irreducible polynomial over \({ \mathbf{F} }_p\)? How about a degree 14 irreducible polynomial?
Question 3.61
How many irreducible polynomials are there of degree 4 over \({ \mathbf{F} }_2\)?
Question 3.62
For each prime p, give a polynomial of degree p that is irreducible over \({ \mathbf{F} }_p\). You can do it in a “uniform” way.
Question 3.63
Can we solve general quadratic equations by radicals? And what about cubics and so on? Why can’t you solve 5th degree equations by radicals?
Question 3.64
Talk about solvability by radicals. Why is \(S_5\) not solvable? Why is \(A_5\) simple?
Question 3.65
For which \(n\) can a regular \(n{\hbox{-}}\)gon be constructed by ruler and compass?
Question 3.66
How do you use Galois theory (or just field theory) to prove the impossibility of trisecting an angle? Doubling a cube? Squaring a circle?
Question 3.67
Which numbers are constructible? Give an example of a non-constructible number whose degree is nevertheless a power of 2.
Question 3.68
State and prove Eisenstein’s Criterion.
Question 3.69
Why is \((x^p - 1)/(x - 1)\) irreducible over \({\mathbf{Q}}\)?
Question 3.70
Can you prove the fundamental theorem of algebra using Galois theory? What do you need from analysis to do so?
Question 3.71
What are the symmetric polynomials?
Question 3.72
State the fundamental theorem of symmetric polynomials.
Question 3.73
Is the discriminant of a polynomial always a polynomial in the coefficients? What does this have to do with symmetric polynomials?
Question 3.74
Find a non-symmetric polynomial whose square is symmetric.
Question 3.75
Let \(f\) be a degree 4 polynomial with integer coefficients. What’s the smallest finite field in which \(f\) necessarily has four roots?
Question 3.76
Define p-adic numbers. What is a valuation?
Question 3.77
What’s Hilbert’s theorem 90?
Question 3.78
Consider a nonconstant function between two compact Riemann Surfaces. How is it related to Galois theory?
Normal Forms
Question 4.1
What is the connection between the structure theorem for modules over a PID and conjugacy classes in the general linear group over a field?
Question 4.2
Explain how the structure theorem for finitely-generated modules over a PID applies to a linear operator on a finite dimensional vector space.
Question 4.3
I give you two matrices over a field. How would you tell if they are conjugate or not? What theorem are you using? State it. How does it apply to this situation? Why is \(k[x]\) a PID? If two matrices are conjugate over the algebraic closure of a field, does that mean that they are conjugate over the base field too?
Question 4.4
If two real matrices are conjugate in \(\operatorname{Mat}(n\times n, {\mathbf{C}})\), are they necessarily conjugate in \(\operatorname{Mat}(n \times N, R)\) as well?
Question 4.5
Give the \(4 \times 4\) Jordan forms with minimal polynomial \((x - 1)(x - 2)^2\).
Question 4.6
Talk about Jordan canonical form. What happens when the field is not algebraically closed?
Question 4.7
What are all the matrices that commute with a given Jordan block?
Question 4.8
How do you determine the number and sizes of the blocks for Jordan canonical form?
Question 4.9
For any matrix A over the complex numbers, can you solve \(B^2 = A\)?
Question 4.10
What is rational canonical form?
Question 4.11
Describe all the conjugacy classes of \(3 \times 3\) matrices with rational entries which satisfy the equation \(A^4 - A^3 - A + 1 = 0\). Give a representative in each class.
Question 4.12
What \(3 \times 3\) matrices over the rationals (up to similarity) satisfy \(f (A) = 0\), where \(f (x) = (x^2 + 2)(x - 1)^3\)? List all possible rational forms.
Question 4.13
What can you say about matrices that satisfy a given polynomial (over an algebraically closed field)? How many of them are there? What about over a finite field? How many such matrices are there then?
Question 4.14
What is a nilpotent matrix?
Question 4.15
When do the powers of a matrix tend to zero?
Question 4.16
If the traces of all powers of a matrix A are 0, what can you say about A?
Question 4.17
When and how can we solve the matrix equation \(\exp(A) = B\)? Do it over the complex numbers and over the real numbers. give a counterexample with real entries.
Question 4.18
Say we can find a matrix \(A\) such that \(\exp(A) = B\) for \(B\) in \(SL_n({\mathbf{R}})\). Does \(A\) also have to be in \({\operatorname{SL}}_n(R)\)? Does \(A\) need to be in \(SL_n(R)\)?
Question 4.19
Is a square matrix always similar to its transpose?
Question 4.20
What are the conjugacy classes of \({\operatorname{SL}}_2({\mathbf{R}})\)?
Question 4.21
What are the conjugacy classes in \(\operatorname{GL}_2({\mathbf{C}})\)?
Matrices and Linear Algebra
Question 5.1
What is a bilinear form on a vector space? When are two forms equivalent? What is an orthogonal matrix? What’s special about them?
Question 5.2
What are the possible images of the unit circle under a linear transformation of \({\mathbf{R}}^2\)?
Question 5.3
Explain geometrically how you diagonalise a quadratic form.
Question 5.4
Do you know Witt’s theorem on real quadratic forms?
Question 5.5
Classify real division algebras.
Question 5.6
Consider the simple operator on C given by multiplication by a complex number. It decomposes into a stretch and a rotation. What is the generalisation of this to operators on a Hilbert space?
Question 5.7
Do you know about singular value decomposition?
Question 5.8
What are the eigenvalues of a symmetric matrix?
Question 5.9
What can you say about the eigenvalues of a skew-symmetric matrix?
Question 5.10
Prove that the eigenvalues of a Hermitian matrix are real and those of a unitary matrix are unitary.
Question 5.11
Prove that symmetric matrices have real eigenvalues and can be diagonalised by orthogonal matrices.
Question 5.12
To which operators does the spectral theorem for symmetric matrices generalise?
Question 5.13
Given a skew-symmetric/skew-Hermitian matrix S, show that \(U = (S + I)(S - I)-1\) is orthogonal/unitary. Then find an expression for \(S\) in terms of \(U\).
Question 5.14
If a linear transformation preserves a nondegenerate alternating form and has \(k\) as an eigenvalue, prove that \(1/k\) is also an eigenvalue.
Question 5.15
State/prove the Cayley–Hamilton theorem.
Question 5.16
Are diagonalisable \(N \times N\) matrices over the complex numbers dense in the space of all \(N \times N\) matrices over the complex numbers? How about over another algebraically closed field if we use the Zariski topology?
Question 5.17
For a linear ODE with constant coefficients, how would you solve it using linear algebra?
Question 5.18
What can you say about the eigenspaces of two matrices that commute with each other?
Question 5.19
What is a Toeplitz operator?
Question 5.20
What is the number of invertible matrices over \({\mathbf{Z}}/p{\mathbf{Z}}\)?
Rings
Question 6.1
State the Chinese remainder theorem in any form you like. Prove it.
Question 6.2
What is a PID? What’s an example of a UFD that is not a PID? Why? Is \(k[x]\) a PID? Why?
Question 6.3
Is \({\mathbf{C}}[x, y]\) a PID? Is \(\left\langle{ x, y }\right\rangle\) a prime ideals in it?
Question 6.4
Do polynomials in several variables form a PID?
Question 6.5
Prove that the integers form a PID.
Question 6.6
Give an example of a PID with a unique prime ideal.
Question 6.7
What is the relation between Euclidean domains and PIDs?
Question 6.8
Do you know a PID that’s not Euclidean?
Question 6.9
Give an example of a UFD which is not a Euclidean domain.
Question 6.10
Is a ring of formal power series a UFD?
Question 6.11
Is a polynomial ring over a UFD again a UFD?
Question 6.12
What does factorisation over \({\mathbf{Q}}[x]\) say about factorisation over \({\mathbf{Z}}[x]\)?
Question 6.13
Give an example of a ring where unique factorisation fails.
Question 6.14
Factor 6 in two different ways in \({\mathbf{Z}}[\sqrt{-5}]\) Is there any way to explain the two factorisations? Factor the ideal generated by 6 into prime ideals.
Question 6.15
What’s the integral closure of \({\mathbf{Z}}\) in \({\mathbf{Q}}(i)\)?
Question 6.16
Find all primes in the ring of Gaussian integers.
Question 6.17
What is a ring of integers? What does “integral over \({\mathbf{Z}}\)” mean?
Question 6.18
Let \({\mathcal{O}}\) be the ring of integers of \({\mathbf{Q}}(d)\), where \(d > 0\). What can you say about the quotient of O by one of its prime ideals?
Question 6.19
Do you know about Dedekind domains and class numbers?
Question 6.20
Talk about factorisation and primes in a polynomial ring. What is irreducibility? For what rings R is it true that \(R[x_1, \cdots , x_n]\) is a unique factorisation domain? What is wrong with unique factorisation if we don’t have a domain? Now, PIDs are Noetherian, but are there UFDs which are not?
Question 6.21
What is the radical of an ideal? What is special about elements in the nilradical?
Question 6.22
Define the “radical” of an ideal. Prove it is an ideal. Prove that the ideal of all polynomials vanishing on the zero set of \(I\) is \(\sqrt{I}\).
Question 6.23.
Do you know what the radical is? Use the fact that the intersection of all prime ideals is the set of all nilpotent elements to prove that \(F [x]\) has an infinite number of prime ideals, where \(F\) is a field.
Question 6.24
What are the radical ideals in \({\mathbf{Z}}\)?
Question 6.25
Give a prime ideal in \({\mathbf{k}}[x, y]\). Why is it prime? What is the variety it defines? What is the Nullstellensatz? Can you make some maximal ideals?
Question 6.26
State/describe Hilbert’s Nullstellensatz. Sketch a proof.
Question 6.27
What is an irreducible variety? Give an example of a non-irreducible one.
Question 6.28
What are the prime ideals and maximal ideals of \({\mathbf{Z}}[x]\)?
Question 6.29
Is the following map an isomorphism? \begin{align*} {\mathbf{Z}}[t] / \left\langle{ t^p - 1 }\right\rangle &\to {\mathbf{Z}}[w] \\ t &\mapsto w \text{ where } w^p = 1 .\end{align*}
Question 6.30
Describe the left, right, and two-sided ideals in the ring of square matrices of a fixed size. Now identify the matrix algebra \(\operatorname{Mat}(n \times n, K)\) with \(\mathop{\mathrm{End}}_K(V )\) where \(V\) is an \(n{\hbox{-}}\)dimensional K-vector space. Try to geometrically describe the simple left ideals and also the simple right ideals via that identification.
Question 6.31
Give examples of maximal ideals in \(K = R \times R \times R \times \cdots\), the product of countably many copies of R. What about for a product of countably many copies of an arbitrary commutative ring \(R\)?
Question 6.32
Consider a commutative ring, \(R\), and a maximal ideal \(I\), what can you say about the structure of \(R/I\)? What if \(I\) were prime?
Question 6.33
Define “Noetherian ring”. give an example.
Question 6.34
Prove the Hilbert basis theorem.
Question 6.35
What is a Noetherian ring? If I is an ideal in a Noetherian ring with a unit, what is the intersection of \(I^n\) over all positive integers \(n\)?
Question 6.36
What is the Jacobson radical? If R is a finitely-generated algebra over a field what can you say about it?
Question 6.37
Give an example of an Artinian ring.
Question 6.38
State the structure theorem for semisimple Artinian rings.
Question 6.39
What is a semisimple algebra? State the structure theorem for semisimple algebras.
Question 6.40
What is a matrix algebra?
Question 6.41
Does \(L_1\) have a natural multiplication with which it becomes an algebra?
Question 6.42.
Consider a translation-invariant subspace of \(L_1\). What can you say about its relation to \(L_2\) as a convolution algebra?
Question 6.43
State the structure theorem for simple rings.
Question 6.44
Do you know an example of a local ring? Another one? What about completions?
Question 6.45
Consider the space of functions from the natural numbers to \({\mathbf{C}}\) endowed with the usual law of addition and the following analogue of the convolution product:
\begin{align*} (f\ast g)(n) = \sum_{d\divides n}^{}f(d) g\qty{n\over d} .\end{align*}
Show that this is a ring. What does this ring remind you of and what can you say about it?
Question 6.46
Prove that any finite division ring is a field (that is, prove commutativity). Give an example of a (necessarily infinite) division ring which is NOT a field.
Question 6.47
Prove that all finite integral domains are fields.
Question 6.48
Can a polynomial over a division ring have more roots than its degree?
Question 6.49
Classify (finite-dimensional) division algebras over \({\mathbf{R}}\).
Question 6.50
Give an example of a \({\mathbf{C}}{\hbox{-}}\)algebra which is not semisimple.
Question 6.51
What is Wedderburn’s theorem? What does the group ring generated by \({\mathbf{Z}}/5{\mathbf{Z}}\) over \({\mathbf{Q}}\) look like?
What if we take the noncyclic group of order 4 instead of \({\mathbf{Z}}/5{\mathbf{Z}}\)? The quaternion group instead of \({\mathbf{Z}}/5{\mathbf{Z}}\)?
Question 6.52
Tell me about group rings. What do you know about them?
Modules
Question 7.1
How does one prove the structure theorem for modules over PID? What is the module and what is the PID in the case of abelian groups?
Question 7.2
If \(M\) is free abelian, how can I put quotients of M in some standard form? What was crucial about the integers here (abelian groups being modules over \({\mathbf{Z}}\))? How does the procedure simplify if the ring is a Euclidean domain, not just a PID?
Question 7.3
Suppose \(D\) is an integral domain and the fundamental theorem holds for finitely-generated modules over \(D\) (i.e. they are all direct sums of finitely many cyclic modules).
Does \(D\) have to be a PID?
Question 7.4
Classify finitely-generated modules over \({\mathbf{Z}}\), over PIDs, and over Dedekind rings.
Question 7.5
Prove a finitely-generated torsion-free abelian group is free abelian.
Question 7.6.
What is a tensor product? What is the universal property? What do the tensors look like in the case of vector spaces?
Question 7.7
Now we’ll take the tensor product of two abelian groups, that is, \({\mathbf{Z}}{\hbox{-}}\)modules. Take \({\mathbf{Z}}/p{\mathbf{Z}}\) and \({\mathbf{Z}}/q{\mathbf{Z}}\), where \(p\) and \(q\) are distinct primes. What is their tensor product?
Question 7.8
What is a projective module?
Question 7.9
What is an injective module?
Question 7.10
Do you know an example of a flat module?
Representation Theory
Question 8.1
Define “representation” of a group. Define “irreducible representation”. Why can you decompose representations of finite groups into irreducible ones? Construct an in- variant inner product.
Question 8.2
State and prove Maschke’s theorem. What can go wrong if you work over the real field? What can go wrong in characteristic p?
Question 8.3
Do you know what a group representation is? Do you know what the trace of a group representation is?
Question 8.4
State/prove/explain Schur’s lemma.
Question 8.5
What can you say about characters? What are the orthogonality relations? How do you use characters to determine if a given irreducible representation is a subspace of another given representation?
Question 8.6
What’s the relation between the number of conjugacy classes in a finite group and the number of irreducible representations?
Question 8.7
What is the character table? What field do its entries lie in?
Question 8.8
Why is the character table a square?
Question 8.9
If \(\chi(g)\) is real for every character \(\chi\), what can you say about \(g\)?
Question 8.10
What’s the regular representation?
Question 8.11
Give two definitions of “induced representation”. Why are they equivalent?
Question 8.12
If you have a representation of \(H\), a subgroup of a group \(G\), how can you induce a representation of \(G\)?
Question 8.13
If you have an irreducible representation of a subgroup, is the induced representation of the whole group still irreducible?
Question 8.14.
What can you say about the kernel of an irreducible representation? How about kernels of direct sums of irreducibles? What kind of functor is induction? Left or right exact?
Question 8.15
What is Frobenius reciprocity?
Question 8.16
Given a normal subgroup \(H\) of a finite group \(G\), we lift all the representations of \(G/H\) to representations of \(G\).
Show that the intersection of the kernels of all these representations is precisely \(H\). What can you say when \(H\) is the commutator subgroup of \(G\)?
Question 8.17
If you have two linear representations \(\pi_1\) and \(\pi_2\) of a finite group \(G\) such that \(\pi_1(g)\) is conjugate to \(\pi_2(g)\) for every g in \(G\), is it true that the two representations are isomorphic?
Question 8.18
Group representations: What’s special about using \({\mathbf{C}}\) in the definition of group algebra?
Is it possible to work over other fields?
What goes wrong if the characteristic of the field divides the order of the group?
Question 8.19
Suppose you have a finite p-group, and you have a representation of this group on a finite-dimensional vector space over a finite field of characteristic p. What can you say about it?
Question 8.20
Let \((\pi, V)\) be a faithful finite-dimensional representation of \(G\). Show that, given any irreducible representation of \(G\), the nth tensor power of \(\operatorname{GL}(V)\) will contain it for some large enough \(n\).
Question 8.21
What are the irreducible representations of finite abelian groups?
Question 8.22
What are the group characters of the multiplicative group of a finite field?
Question 8.23
Are there two nonisomorphic groups with the same representations?
Question 8.24
If you have a \({\mathbf{Z}}/5{\mathbf{Z}}\) action on a complex vector space, what does this action look like? What about an \(S_3\) action? A dihedral group of any order?
Question 8.25
What are the representations of \(S_3\)? How do they restrict to \(S_2\)?
Question 8.26
Tell me about the representations of \(D_4\). Write down the character table. What is the 2-dimensional representation? How can it be interpreted geometrically?
Question 8.27
How would you work out the orders of the irreducible representations of the dihedral group \(D_n\)?
Why is the sum of squares of dimensions equal to the order of the group?
Question 8.28
Do you know any representation theory? What about representations of \(A_4\)?
Give a nontrivial one. What else is there? How many irreducible representations do we have? What are their degrees? Write the character table of \(A_4\).
Question 8.29
Write the character table for \(S_4\).
Question 8.30
Start constructing the character table for \(S_5\).
Question 8.31.
How many irreducible representations does \(S_n\) have?
What classical function in mathematics does this number relate to?
Question 8.32
Discuss representations of \({\mathbf{Z}}\), the infinite cyclic group. What is the group algebra of \({\mathbf{Z}}\)?
Question 8.33
What is a Lie group? Define a unitary representation. What is the Peter–Weyl theorem? What is the Lie algebra? The Jacobi identity? What is the adjoint representation of a Lie algebra? What is the commutator of two vector fields on a manifold?
When is a representation of \({\mathbf{Z}}\) completely reducible? Why?
Which are the indecomposable modules?
Question 8.34
Talk about the representation theory of compact Lie groups. How do you know you have a finite-dimensional representation?
Question 8.35
How do you prove that any finite-dimensional representation of a compact Lie group is equivalent to a unitary one?
Question 8.36
Do you know a Lie group that has no faithful finite-dimensional representations?
Question 8.37
What do you know about representations of \({\operatorname{SO}}(2)\)? \({\operatorname{SO}}(3)\)?
Categories and Functors
Question 9.1
Which is the connection between Hom and tensor product? What is this called in representation theory?
Question 9.2
Can you get a long exact sequence from a short exact sequence of abelian groups together with another abelian group?
Question 9.3
Do you know what the Ext functor of an abelian group is? Do you know where it appears? What is \(\operatorname{Ext}({\mathbf{Z}}/m{\mathbf{Z}}, {\mathbf{Z}}/n{\mathbf{Z}})\)? What is \(\operatorname{Ext}({\mathbf{Z}}/m{\mathbf{Z}}, {\mathbf{Z}})\)?