Galois Theory
Theory
- Show that if \(K/F\) is the splitting field of a separable polynomial then it is Galois.
- Show that any quadratic extension of a field \(F\) with \(\operatorname{ch}(F)\neq 2\) is Galois.
-
Show that if \(K/E/F\) with \(K/F\) Galois then \(K/E\) is always Galois with \(g(K/E) \leq g(K/F)\).
- Show additionally \(E/F\) is Galois \(\iff g(K/E) {~\trianglelefteq~}g(K/F)\).
- Show that in this case, \(g(E/F) = g(K/F) / g(K/E)\).
- Show that if \(E/k, F/k\) are Galois with \(E\cap F = k\), then \(EF/k\) is Galois and \(G(EF/k) \cong G(E/k)\times G(F/k)\).
Computations
- Show that the Galois group of \(x^n - 2\) is \(D_n\), the dihedral group on \(n\) vertices.
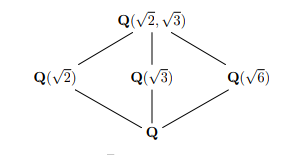
- Compute all intermediate field extensions of \({\mathbf{Q}}(\sqrt 2, \sqrt 3)\), show it is equal to \({\mathbf{Q}}(\sqrt 2 + \sqrt 3)\), and find a corresponding minimal polynomial.
- Compute all intermediate field extensions of \({\mathbf{Q}}(2^{1\over 4}, \zeta_8)\).
- Show that \({\mathbf{Q}}(2^{1\over 3})\) and \({\mathbf{Q}}(\zeta_3 2^{1\over 3})\)
- Show that if \(L/K\) is separable, then \(L\) is normal \(\iff\) there exists a polynomial \(p(x) = \prod_{i=1}^n x- \alpha_i\in K[x]\) such that \(L = K(\alpha_1, \cdots, \alpha_n)\) (so \(L\) is the splitting field of \(p\)).
- Is \({\mathbf{Q}}(2^{1\over 3})/{\mathbf{Q}}\) normal?
- Show that \({\mathbf{GF}}(p^n)\) is the splitting field of \(x^{p^n} - x \in { \mathbf{F} }_p[x]\).
- Show that \({\mathbf{GF}}(p^d) \leq {\mathbf{GF}}(p^n) \iff d\divides n\)
- Compute the Galois group of \(x^n - 1 \in {\mathbf{Q}}[x]\) as a function of \(n\).
- Identify all of the elements of the Galois group of \(x^p-2\) for \(p\) an odd prime (note: this has a complicated presentation).
- Show that \({ \operatorname{Gal}}(x^{15}+2)/{\mathbf{Q}}\cong S_2 \rtimes{\mathbf{Z}}/15{\mathbf{Z}}\) for \(S_2\) a Sylow \(2{\hbox{-}}\)subgroup.
- Show that \({ \operatorname{Gal}}(x^3+4x+2)/{\mathbf{Q}}\cong S_3\), a symmetric group.