If \(f: [a, b] \to {\mathbf{R}}\) is continuous on a closed interval and differentiable on \((a, b)\), then there exists \(\xi \in [a, b]\) such that \begin{align*} f(b) - f(a) = f'(\xi)(b-a) .\end{align*}
More generally, if \(g: [a,b]\to {\mathbf{R}}\) is similarly continuous on \([a, b]\) and differentiable on \((a, b)\), then there exists a \(\xi\) with \begin{align*} \qty{ f(b) - f(c) } g'(\xi) = \qty{g(b) - g(a)} f'(\xi) .\end{align*} What this means graphically:
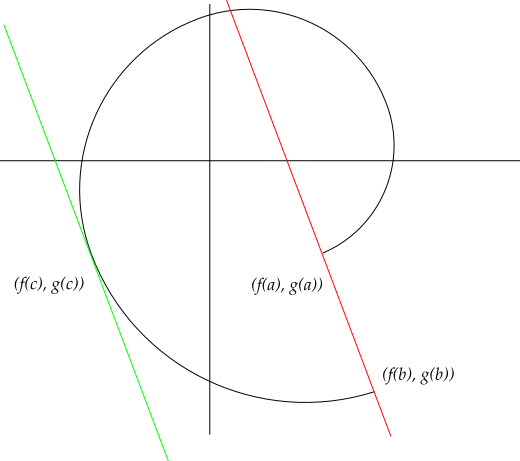
If \(\left\{{f_n}\right\}\) is a sequence of functions where
- each \(f_n\) is differentiable,
- there is some \(G\) such that \({\left\lVert { \sum_{n\leq N} f_n' - G} \right\rVert}_\infty \overset{N\to\infty}\longrightarrow 0\), and
- there exists at least one point 1 \(x_0\) such that \(\sum f_n(x)\) converges (pointwise),
then there exists an \(F\) such that 2 \begin{align*} {\left\lVert { \sum_{n\leq N} f_n - F} \right\rVert}_\infty \overset{N\to\infty}\longrightarrow 0 && F' = g .\end{align*}
A function \(f: (a, b) \to {\mathbf{R}}\) is Lipschitz \(\iff f\) is differentiable and \(f'\) is bounded. In this case, \({\left\lvert {f'(x)} \right\rvert} \leq C\), the Lipschitz constant.
\begin{align*} f(x) \coloneqq \begin{cases} x^2 \sin\qty{1\over x^2} & x\neq 0 \\ 0 & x=0. \end{cases} .\end{align*}
Note that \(f\) is differentiable at \(x=0\) since \({1\over h}{\left\lvert {f(h) - f(0)} \right\rvert} = {\left\lvert { h\sin\qty{h^{-2}}} \right\rvert}\leq {\left\lvert {h} \right\rvert}\to 0\), and \begin{align*} f'(x) = 2x\sin\qty{1\over x^2 } - \qty{2\over x}\cos\qty{1\over x^2} \chi_{x\neq 0} .\end{align*} now take the sequence \(x_n \coloneqq 1/\sqrt{k\pi}\) to get \(f'(x_n) = 2\sqrt{k\pi}(-1)^k \overset{n\to\infty}\longrightarrow\infty\).