Calculus Preliminaries

Derivatives

proposition (Contraction principle):

If $(X, {\left\lvert {{-}} \right\rvert})$ is a metric space and $f: X\to X$ with $\begin{align*} {\left\lvert {f(x) - f(y)} \right\rvert} \leq c {\left\lvert {x-y} \right\rvert} \text{ for some }c < 1, \forall x, y\in X ,\end{align*}$ then $f$ is a contraction. If $X$ is complete, then $f$ has a unique fixed point $x_0$ such that $f(x_0) = x_0$ .

proof (?):

Uniqueness: if $x, y$ are two fixed points, then $\begin{align*} 0 \leq {\left\lvert {x-y} \right\rvert} = {\left\lvert {f(x) - f(y)} \right\rvert}\leq c {\left\lvert {x-y} \right\rvert}\leq {\left\lvert {x-y} \right\rvert} ,\end{align*}$ forcing ${\left\lvert {x-y} \right\rvert} = 0$

Existence: Define a sequence by picking $x_0$ arbitrarily and setting $x_k \coloneqq f(x_{k-1})$ . Then $\begin{align*} {\left\lvert {x_{k+1}-x_k} \right\rvert} = {\left\lvert {f(x_k) - f(x_{k-1}) } \right\rvert} \leq c{\left\lvert {x_k - x_{k-1}} \right\rvert} ,\end{align*}$ so inductively $\begin{align*} {\left\lvert {x_{k+1}- x_k} \right\rvert}\leq c^k {\left\lvert {x_1 - x_0} \right\rvert} .\end{align*}$ The claim is that this makes $\left\{{x_k}\right\}$ a Cauchy sequence, this follows from the fact that if $n < m$ then $\begin{align*} {\left\lvert {x_n - x_m} \right\rvert} \leq \sum_{n+1\leq k \leq m} {\left\lvert {x_k - x_{k-1}} \right\rvert} \leq \sum_{n \leq k \leq m-1} c^k {\left\lvert {x_1 - x_0} \right\rvert} \leq c^n {\left\lvert {x_1 - x_0 \over 1-c} \right\rvert} \to 0 .\end{align*}$

Implicit Function Theorem

theorem (Implicit Function Theorem):

Suppose $f\in C^1({\mathbb{R}}^{n+m}, {\mathbb{R}}^n)$ , that $f(a, b) = 0$ , and the derivative $D_f(a, b)$ at $(a, b)$ is an invertible linear map. Then there exists a neighborhood $U\subseteq {\mathbb{R}}^n$ containing $a$ and a unique $g\in C^1(U, {\mathbb{R}}^m)$ such that $g(a) = b$ and $f(a, g(a)) = 0$ for all $x\in U$ .

slogan:

A relation is locally the graph of a function wherever the derivative is nonsingular.

Inverse Function Theorem

theorem (Inverse Function Theorem):

For $f \in C^1({\mathbb{R}}; {\mathbb{R}})$ with $f'(a) \neq 0$ , then $f$ is invertible in a neighborhood $U \ni a$ , $g\coloneqq f^{-1}\in C^1(U; {\mathbb{R}})$ , and at $b\coloneqq f(a)$ the derivative of $g$ is given by $\begin{align*} g'(b) = {1 \over f'(a)} .\end{align*}$ For $F \in C^1({\mathbb{R}}^n, {\mathbb{R}}^n)$ with $D_f$ invertible in a neighborhood of $a$ , so $\operatorname{det}(J_f)\neq 0$ , then setting $b\coloneqq F(a)$ , $\begin{align*} J_{F^{-1}}(q) = \qty{J_F(p)}^{-1} .\end{align*}$

The version for holomorphic functions: if $f\in \mathop{\mathrm{Hol}}({\mathbb{C}}; {\mathbb{C}})$ with $f'(p)\neq 0$ then there is a neighborhood $V\ni p$ with that $f\in \mathop{\mathrm{BiHol}}(V, f(V))$ .

slogan:

A $C^1$ function is invertible in any neighborhood in which its derivative $f'$ is invertible.

remark:

Recall that absolutely convergent implies convergent, but not conversely: $\sum k^{-1}= \infty$ but $\sum (-1)^k k^{-1}< \infty$ . This converges because the even (odd) partial sums are monotone increasing/decreasing respectively and in $(0, 1)$ , so they converge to a finite number. Their difference converges to 0, and their common limit is the limit of the sum.

Integrals

Green’s Theorem

theorem (Green's Theorem):

If $\Omega \subseteq {\mathbb{C}}$ is bounded with ${{\partial}}\Omega$ piecewise smooth and $f, g\in C^1(\mkern 1.5mu\overline{\mkern-1.5mu\Omega\mkern-1.5mu}\mkern 1.5mu)$ , then $\begin{align*}\int_{{{\partial}}\Omega} f\, dx + g\, dy = \iint_{\Omega} \qty{ {\frac{\partial g}{\partial x}\,} - {\frac{\partial f}{\partial y}\,} } \, \,dA.\end{align*}$ In vector form, $\begin{align*} \int_\gamma F\cdot \,dr= \iint_R \operatorname{curl}F \,dA .\end{align*}$ As a consequence, areas can be computed as $\begin{align*} \mu(\Omega) = {1\over 2}\oint_{{{\partial}}\Omega} \qty{y\,dx- x\,dy} = \oint_{{{\partial}}\Omega} x\,dy= -\oint_{{{\partial}}\Omega} y\,dx .\end{align*}$

In general, $\mu(\Omega) = \int_{\Omega} {\left\lvert {f'(z)} \right\rvert} \,dz$ .

remark:

Some basic facts needed for line integrals in the plane:

Green’s theorem requires $C^1$ partial derivatives.
$\operatorname{grad}f = {\left[ { {\frac{\partial f}{\partial x}\,}, {\frac{\partial f}{\partial y}\,} } \right]}$ .
- If $F = \operatorname{grad}f$ for some $f$ , $F$ is a vector field.
Given $f(x, y)$ and $\gamma(t)$ , the chain rule yields ${\frac{\partial }{\partial t}\,} (f\circ \gamma)(t) = {\left\langle { \operatorname{grad}f\circ \gamma)(t)},~{\gamma'(t)} \right\rangle}$ .
For $F(x, y) = {\left[ {M(x, y), N(x, y)} \right]}$ , $\operatorname{curl}F = {\frac{\partial N}{\partial x}\,} - {\frac{\partial M}{\partial y}\,}$ and $\operatorname{Div}F = {\frac{\partial M}{\partial x}\,} + {\frac{\partial N}{\partial y}\,}$ .
$\int_\gamma F\cdot \,dr= \int_a^b F(\gamma(t))\cdot \gamma'(t) \,dt$ .

Stokes Theorem

theorem (Stokes Theorem):

Suppose $\omega \coloneqq f(z)\,dz$ is a differential 1-form on an orientable manifold $\Omega$ , then $\begin{align*}\int_{{{\partial}}\Omega}\omega = \int_\Omega d\omega \qquad \text{i.e.} \qquad \int_{{{\partial}}\Omega}f(z)\,dz= \int_\Omega d(f(z)\,dz)\end{align*}$

Series and Sequences

fact (Partial Fraction Decomposition):

For every root $r_i$ of multiplicity 1, include a term $A/(x-r_i)$ .
For any factors $g(x)$ of multiplicity $k$ , include terms $A_1/g(x), A_2/g(x)^2, \cdots, A_k / g(x)^k$ .
For irreducible quadratic factors $h_i(x)$ , include terms of the form ${Ax+B \over h_i(x)}$ .

proposition (Uniform Convergence of Series):

A series of functions $\sum_{n=1}^\infty f_n(x)$ converges uniformly iff $\begin{align*} \lim_{n\to \infty} {\left\lVert { \sum_{k\geq n} f_k } \right\rVert}_\infty = 0 .\end{align*}$

theorem (Weierstrass $M\dash$Test):

If $\left\{{f_n}\right\}$ with $f_n: \Omega \to {\mathbb{C}}$ and there exists a sequence $\left\{{M_n}\right\}$ with ${\left\lVert {f_n} \right\rVert}_\infty \leq M_n$ and $\sum_{n\in {\mathbb{N}}} M_n < \infty$ , then $f(x) \coloneqq\sum_{n\in {\mathbb{N}}} f_n(x)$ converges absolutely and uniformly on $\Omega$ . Moreover, if the $f_n$ are continuous, by the uniform limit theorem, $f$ is again continuous.

remark:

Note that if a power series converges uniformly, then summing commutes with integrating or differentiating.

proposition (Ratio Test):

Consider $\sum c_k z^k$ , set $R = \lim {\left\lvert {c_{k+1} \over c_k} \right\rvert}$ , and recall the ratio test:

$R\in (0, 1) \implies$ convergence.
$R\in (1, \infty] \implies$ divergence.
$R=1$ yields no information.

proposition (Root Test):

figures/image_2021-05-27-15-40-58.png

proposition (Radius of Convergence by the Root Test):

For $f(z) = \sum_{k\in {\mathbb{N}}} c_k z^k$ , defining $\begin{align*} {1\over R} \coloneqq\limsup_{k} {\left\lvert {a_k} \right\rvert}^{1\over k} ,\end{align*}$ then $f$ converges absolutely and uniformly for $D_R \coloneqq{\left\lvert {z} \right\rvert} < R$ and diverges for ${\left\lvert {z} \right\rvert} > R$ . So the radius of convergence is given by $\begin{align*} R = {1\over \limsup_n {\left\lvert {a_n} \right\rvert}^{1\over n}} .\end{align*}$

Moreover $f$ is holomorphic in $D_R$ , can be differentiated term-by-term, and $f' = \sum_{k\in {\mathbb{N}}} n c_k z^k$ .

proposition (The $p\dash$test):

Recall the $p{\hbox{-}}$ test: $\begin{align*} \sum n^{-p} < \infty \iff p \in (1, \infty) .\end{align*}$

Function Convergence

definition (Locally uniform convergence):

A sequence of functions $f_n$ is said to converge locally uniformly on $\Omega \subseteq {\mathbb{C}}$ iff $f_n\to f$ uniformly on every compact subset $K \subseteq \Omega$ .

Exercises

exercise (Line integrals):

Compute $\int_\Gamma \Re(z) \,dz$ for $\Gamma$ the unit square.

#complex/exercise/completed

solution:

Write $\Gamma = \sum_{1\leq k \leq 4}\gamma_k$ , starting at zero and traversing clockwise:

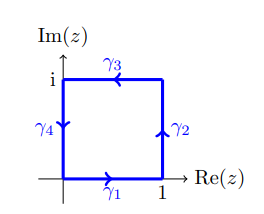
figures/2021-12-19_03-22-20.png

Compute:

$\gamma_1$ : parameterize to get $\int_0^1t1\,dt= 1/2$ .
$\gamma_2$ : $\int_0^1 i \,dt= i$
$\gamma_2$ : $-\int_0^1 (1-t)\,dt= -1/2$
$\gamma_2$ : $- \int_0^1 0 \,dt= 0$

So $\int_\Gamma \Re(z) \,dz= i$ .

exercise (?):

Show that if $f$ is a differentiable contraction, $f$ is uniformly continuous.

#complex/exercise/work

exercise (Uniform limit theorem):

Show that a continuous function on a compact set is uniformly continuous.

#complex/exercise/work

exercise (?):

Show that a uniform limit of continuous functions is continuous, and a uniform limit of uniformly continuous functions is uniformly continuous. Show that this is not true if uniform convergence is weakened to pointwise convergence.

#complex/exercise/completed

solution:

Suppose ${\left\lVert {f_n - f} \right\rVert}_\infty\to 0$ , fix ${\varepsilon}$ , we then need to produce a $\delta$ so that $\begin{align*} {\left\lvert {z-w} \right\rvert}\leq \delta \implies {\left\lvert {f(z) - f(w) } \right\rvert} < {\varepsilon} .\end{align*}$

Write $\begin{align*} {\left\lvert {f(z) - f(w)} \right\rvert} \leq {\left\lvert {f(z) - f_n(z)} \right\rvert} + {\left\lvert {f_n(z) - f_n(w)} \right\rvert} + {\left\lvert {f_n(w) - f(w)} \right\rvert} .\end{align*}$

Bound the first term by ${\varepsilon}/3$ using that $f_n\to f$
Bound the second term by ${\varepsilon}/3$ using that $f_n$ is continuous
Bound the third term by ${\varepsilon}/3$ using that $f_n\to f$
Pick $\delta$ to be the minimum $\delta$ supplied by these three bounds.

Why uniform convergence is necessary: need these bounds to holds for all $z, w$ where ${\left\lvert {z-w} \right\rvert} < \delta$ . Why pointwise convergence doesn’t work: $f_n(z) \coloneqq z^n \overset{n\to\infty}\longrightarrow\chi_{z=1}$

For uniform continuity: take $\sup_{z, w}$ on both sides: $\begin{align*} \sup_{z, w} {\left\lvert {f(z) - f(w)} \right\rvert} &\leq \sup_{z} {\left\lvert {f(z) - f_n(z)} \right\rvert} + \sup_{z, w} {\left\lvert {f_n(z) - f_n(w)} \right\rvert} + \sup_{w} {\left\lvert {f_n(w) - f(w)} \right\rvert} \\ &\leq {\left\lVert {f - f_n} \right\rVert}_\infty + \sup_{z, w} {\left\lvert {f_n(z) - f_n(w)} \right\rvert} + {\left\lVert {f-f_n} \right\rVert}_\infty ,\end{align*}$ where now the middle term is bounded by uniform continuity of $f_n$ .

exercise (?):

Determine where the following real-valued function is or is not uniformly convergent: $\begin{align*} f_n(x) \coloneqq{\sin(nx)\over 1+nx} .\end{align*}$

#complex/exercise/completed

solution:

This converges uniformly on $[a, \infty)$ for $a$ any constant: $\begin{align*} {\left\lvert {\sin(nx) \over 1+nx} \right\rvert} \leq {1\over 1 + na} < {\varepsilon}= {\varepsilon}(n, a) .\end{align*}$

This does not converge uniformly on $(0, \infty)$ : $\begin{align*} x_n \coloneqq{1\over n} \implies {\left\lvert {f_n(x_n)} \right\rvert} = {\left\lvert {\sin(1) \over 2} \right\rvert} > {\varepsilon} .\end{align*}$

exercise (?):

Show that $\sum_{k\geq 0}z^k/k!$ converges locally uniformly to $e^z$ .

#complex/exercise/completed

solution:

Apply the $M{\hbox{-}}$ test on a compact set $K$ with $z\in K \implies {\left\lvert {z} \right\rvert} \leq M$ : $\begin{align*} {\left\lVert {e^z - \sum_{0\leq k \leq n} z^k/k!} \right\rVert}_\infty &= {\left\lVert {\sum_{k\geq n+1}z^k/k! } \right\rVert}_{\infty} \\ &\leq \sum_{k\geq n+1} {\left\lVert {z} \right\rVert}_\infty^k /k! \\ &\leq \sum_{k\geq 0} {\left\lVert {z} \right\rVert}_\infty^k /k! \\ &= e^{{\left\lVert {z} \right\rVert}_\infty} \\ &\leq e^{{\left\lvert {M} \right\rvert}} \\ &< \infty .\end{align*}$

exercise (?):

Show that if $f_n\to f$ uniformly then $\int_\gamma f_n\to \int_\gamma f$ .

#complex/exercise/completed

solution:

$\begin{align*} {\left\lvert { \int_\gamma f_n(z) \,dz- \int_\gamma f(z) \,dz } \right\rvert} &= {\left\lvert {\int_\gamma f_n(z) - f(z) \,dz} \right\rvert} \\ &\leq \int_\gamma {\left\lvert {f_n - f} \right\rvert} {\left\lvert {\,dz} \right\rvert} \\ &\leq \int_\gamma {\left\lVert {f_n - f} \right\rVert}_{\infty, \gamma} \cdot {\left\lvert {\,dz} \right\rvert} \\ &= {\varepsilon}\cdot \mathop{\mathrm{length}}(\gamma) \\ &\overset{n\to\infty}\longrightarrow 0 .\end{align*}$