Define $\qty{n}^{ (k) } $ to be the rising factorial \begin{align*} \qty{n}^{ (k) } = n(n+1)(n+2) \cdots (n+(k-1)) = k! {n+k-1\choose k} ,\end{align*} which has exactly \(k\) terms. Some useful identities: \begin{align*} \qty{n}^{ (k) } &= {(n+k-1)! \over (k-1)!} = {\Gamma(n+k) \over \Gamma(n)} \\ { \qty{n}^{ (k) } \over k!} &= {n+k-1 \choose k} .\end{align*}
Similarly define the falling factorial \begin{align*} \qty{n}_{ (k) } = n(n-1)(n-2)\cdots(n-(k-1)) = k!{n\choose k} ,\end{align*} which again has \(k\) terms. \begin{align*} \qty{n}_{ (k) } &= {n! \over (n-k)!} = {\Gamma(n+1) \over \Gamma(n - (k-1))}\\ { \qty{n}_{ (k) } \over k!} &= {n\choose k} .\end{align*}
Where this comes up most often: \begin{align*} \qty{{\frac{\partial }{\partial z}\,}}^k z^n = \qty{n}_{ (k) } \, z^{n-k} .\end{align*}
Extend the binomial coefficients to negative numbers in the following way: \begin{align*} {-n \choose k} &\coloneqq(-n)(-(n+1))\cdots (-(n + (k-1))) \cdot {1\over k!} = (-1)^k {n+k-1 \choose k} .\end{align*} Then \begin{align*} (x+y)^n = \sum_{k\geq 0} {n\choose k} x^{k}y^{n-k} .\end{align*}
\begin{align*} \sum_{k=1}^{n} k &=\frac{n(n+1)}{2} \\ \sum_{k=1}^{n} k^{2} &=\frac{n(n+1)(2 n+1)}{6} \\ \sum_{k=1}^{n} k^{3} &=\frac{n^{2}(n+1)^{2}}{4} \\ \sum_{0\leq k \leq N} z^k &= {1 - z^{N+1} \over 1-z} \\ {1\over 1-z} &= \sum_{k\geq 0} z^k \\ e^z &= \sum_{k\geq 0} {z^k \over k!} \\ \sin(z) &= \sum_{\substack{ k \geq 1 \\ \text{odd} }} (-1)^{k+1 \over 2} {z^k \over k!} \\ &= z - {1\over 3!}z^3 + {1\over 5!}z^5 + \cdots \\ \\ \cos(z) &= \sum_{\substack{ k \geq 0 \\ \text{even}} } (-1)^{k\over 2} {z^k \over k!} \\ &= 1 - {1\over 2!}z^2 + {1\over 4!}z^4 + \cdots \\ \\ \cosh(z) &= \sum_{k\geq 0} { z^{2k} \over (2k)! } \\ &= 1 + {1\over 2!}z^2 + {1\over 4!}z^4 + \cdots \\ \\ \sinh(z) &= \sum_{k\geq 0} { z^{2k+1} \over (2k+1)! } \\ &= z + {1\over 3!}z^3 + {1\over 5!}z^5 + \cdots \\ \\ \log(1-z) &= -1\cdot \sum_{k \geq 1} {z^k\over k} \quad {\left\lvert {z} \right\rvert} < 1 \\ \\ \qty{{\frac{\partial }{\partial z}\,}}^k \sum_{n=0}^\infty c_n z^n &= \sum_{n=k}^\infty (n)_k \, c_n z^{n-k} \\ &= \sum_{n=k}^\infty n(n-1)\cdots(n-k+1) c_n z^{n-k} \\ (1+z)^{1/2} &= \sum_{k\geq 0} {1/2 \choose k}z^k,\qquad {\left\lvert {z} \right\rvert} < 1 \\ &= 1 + (1/2)z + {(1/2)(-1/2) \over 2!}z^2 + {(1/2)(-1/2)(-3/2) \over 3!}z^3 + \cdots \\ &= 1 + {1\over 2}z - {1\over 8}z^2 + {1\over 16}z^3 - \cdots \\ (1+z)^{\alpha} &= \sum_{k\geq 0} {\alpha \choose k}z^k,\qquad {\left\lvert {z} \right\rvert} < 1 \\ {1\over 1+z^n} &= \sum_{k\geq 0} {n+k-1 \choose k} (-z)^k, \qquad {\left\lvert {z} \right\rvert} < 1 \end{align*}
Some other classes of series to remember: \begin{align*} \sum_{k=1}^{n} k &= \frac{n(n+1)}{2} \\ \sum_{k=1}^{n} k(k+1) &= \frac{n(n+1)(n+2)}{3} \\ \sum_{k=1}^{n} k(k+1)(k+2) &= \frac{n(n+1)(n+2)(n+3)}{4} \\ \vdots \quad & \vdots \\ \sum_{k=1}^{n} k^{(p)} &= \frac{n^{(p+1)}}{p+1} && k^{(p)}\coloneqq k(k+1)(k+2) \cdots (k+p-1) .\end{align*} How to remember: compare to the integral \begin{align*} \int_{x=0}^{x=n} x^p \,dx= { n^{p+1} \over p+1} .\end{align*}
Remembering that \(\sum_{1\leq k \leq n} k = n(n+1)/2\): realize as counting a triangle, flip to count an entire rectangle of size \(n\times (n+1)\) and take half:
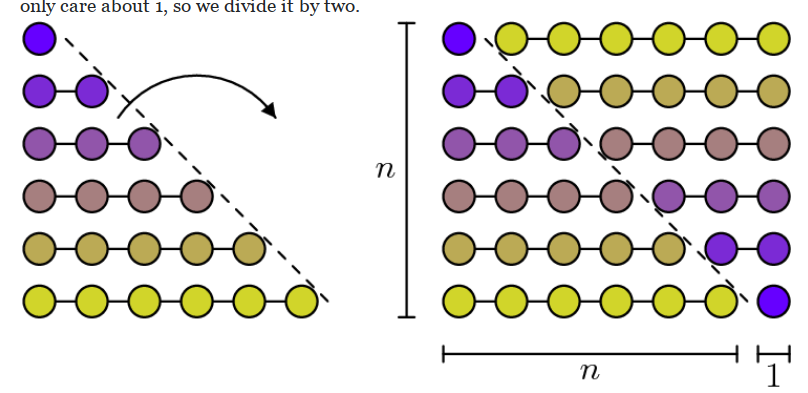
Write \(k^2 = k(k+1) - k\) to get \begin{align*} \sum k^2 = \sum k(k+1) - \sum k = {n(n+1/2)(n+2/2) \over 3} .\end{align*} Similarly \(\sum k^3 = (\sum k )^2\).
For summing the odds, \(\sum_{k\geq 1} (2k-1)\):

For denominators: \begin{align*} \sum_{k=1}^{n} \frac{1}{k(k+1)}=\frac{1}{1}-\frac{1}{n+1} \\ \sum_{k=1}^{n} \frac{2}{k(k+1)(k+2)}=\frac{1}{1 \cdot 2}-\frac{1}{(n+1)(n+2)} \\ \sum_{k=1}^{n} \frac{p}{k^{(p+1)}}=\frac{1}{1^{(p)}}-\frac{1}{(n+1)^{(p)}} ,\end{align*} where \(1^{(p)} \coloneqq p!\). How to remember the last one: \begin{align*} \int_{x=1}^{x=n+1}{p\over x^{p+1}}\,dx= {1\over 1^p} - {1\over (n+1)^p} .\end{align*}
\begin{align*} \sqrt{z} &= \sqrt{z_0 + z - z_0} \\ &= \sqrt{z_0 \qty{ 1 + {z-z_0 \over z} }} \\ &= \sqrt{z_0} \sqrt{1+u},\quad u\coloneqq{z-z_0 \over z} \\ \implies \sqrt{z} &= \sqrt{z_0} \sum_{k\geq 0} {1/2 \choose k} \qty{z- z_0 \over z}^k .\end{align*}
The product of two sequences is given by the Cauchy product \begin{align*} \sum a_kz^k \cdot \sum b_k z^k = \sum c_k z^k,\quad c_k \coloneqq\sum_{j\leq k} a_k b_{k-j} .\end{align*}
Inverting Series
Cauchy product formula for coefficients of \(1/A(z)\)
Using the general ring theory fact that \(A(z) \coloneqq\sum_{k\geq 0} a_k z^k \in R[[z]]\) is invertible iff \(a_0\) is invertible in \(R\), power series over fields can always be inverted. There is a formula: writing \(B(z) \coloneqq\sum_{k\geq 0 } b_k z^k \coloneqq 1/A(z) \in {\mathbb{C}}[[z]]\), the coefficients can be inductively computed as \begin{align*} b_0 &= a_0^{-1}\\ b_n &= -a_0^{-1}\sum_{1\leq i \leq n} a_i b_{n-i} \\ &= -a_0^{-1}\sum_{0\leq i \leq n-1} a_{n-i}b_i \\ &= -{1\over a_0}\qty{a_nb_0 + a_{n-1}b_1 + \cdots + a_1 b_{n-1} } .\end{align*}
How to prove this: \begin{align*} \qty{\sum a_k z^k}\qty{\sum b_k z^k} = 1 \implies a_0b_0 &=1 \\ a_0b_1 + a_1b_0 &= 1 \\ a_0b_2 + a_1b_1 + a_2b_0 &= 1 \\ \vdots \quad&\quad \vdots \end{align*}
Use this formulation to show that if \(A(z)= 1-z\) then \(1/A(z) = \sum z^k\).
Noting \(a_0 = 1, a_1 = -1\), we have
- \(b_0 = 1/a_0 = 1\)
- \(b_1 = -{1\over a_0}(a_1 b_0) = -1(-1\cdot 1) = 1\)
- \(b_2 = -{1\over a_0}(a_2 b_0 + a_1 b_1) = -1(0\cdot 1 + -1\cdot 1) = 1\),
and so on, so \begin{align*} {1\over A(z)} = 1 + 1\cdot z + 1\cdot z^2 + \cdots .\end{align*}
Let \(A(z) \coloneqq 2z-1\) and find \(1/A(z)\).
To compute the inverse of \(A(z) \coloneqq(2z-1)\), note \(a_0 = -1, a_1 = 2\), so
- \(b_0 = 1/a_0 = -1\)
- \(b_1 = -{1\over a_0}(a_1b_0) = 1(2\cdot -1) = -2\)
- \(b_2 = -{1\over a_0}(a_2 b_0 + a_1 b_1) = 1(0\cdot 1 + 2\cdot -2) = -4\)
- \(b_3 = -{1\over a_0}(a_3b_0 + a_2 b_1 + a_1 b_2) = 1(0 + 0 + 2\cdot -4) = -8\)
so \begin{align*} {1\over 1-2z} = -1 - 2z - 4z^2 - 8z^3 \cdots = - \sum_{k\geq 0} (2z)^k .\end{align*}
Find \(1/\cos(z)\) using this method.
We have \(\cos(z) = c_0 +c_2^2 + c_4 z^4 + { \mathsf{O}} (z^6)\) where
- \(c_0 = 1\)
- \(c_2 = -1/2!\)
- \(c_4 = 1/4!\)
Note that \(c_i\) for \(i\) odd all vanish. Write \(1/\cos(z) = \sum b_k z^k\), then
- \(b_0 = c_0^{-1}= 1\).
- \(b_1 = -c_0^{-1}(c_1 b_0) = -(0) = 0\).
- \(b_2 = -c_0^{-1}(c_2 b_0 + c_1b_1) = -(c_2 + 0) = -c_2 = 1/2!\)
- \(b_3 = -c_0^{-1}(c_3b_0 + c_2b_1 + c_1b_2) = -(0 +0 + 0)= 0\)
- \(b_4 = -c_0^{-1}(c_4b_0 + c_3b_1 + c_2 b_2 + c_1b_3)=-(c_4 + 0 + (-1/2!)(1/2!) + 0) = 5/24\).
So \begin{align*} {1\over \cos(z)} = 1 + {1\over 2!}z^2 + {5\over 24}z^4 + { \mathsf{O}} (z^6) .\end{align*}
Find \(1/\sin(z)\) using this method.
Note that the leading coefficient of the expansion for \(\sin(z)\) is 0, so this can’t be inverted directly. A standard trick: factor out the smallest power of \(z\) to get a piece with a nonzero leading coefficient, and invert that instead. Write \begin{align*} \sin(z) = z - {1\over 3!}z^3 + {1\over 5!}z^5 - { \mathsf{O}} (z^7) = z f(z) \coloneqq z(1 + c_2z^2 + c_4 z^4 + { \mathsf{O}} (z^6)) ,\end{align*} where
- \(c_0 = 1\)
- \(c_2 = -{1\over 3!}\)
- \(c_4 = {1\over 5!}\)
- \(c_i = 0\) for \(i\) odd.
Writing \(B(z) \coloneqq{1\over f(z)} = \sum b_k z^k\), we have
- \(b_0 = c_0^{-1}= 1\)
- \(b_2 = -(c_2 b_0 + c_1 b_1) = -c_2\)
- \(b_4 = -(c_4 b_0 + c_2 b_2) = c_2^2 - c_4\)
Thus \(1/B(z) = 1 -c_2z^2 + (c_2^2-c_4)z^4 + { \mathsf{O}} (z^6)\), and \begin{align*} {1\over \sin(z)} &= {1\over z} {1\over B(z)} \\ &= {1\over z} - c_2 z + (c_2^2 - c_4)z^3 + { \mathsf{O}} (z^5) \\ &= {1\over z} + {1\over 3!} z + ({1\over 3! 3!} - {1\over 5!})z^3 + { \mathsf{O}} (z^5) \\ &= {1\over z} + {1\over 3!}z + {7\over 360}z^3 + { \mathsf{O}} (z^5) .\end{align*}
Geometric Series
Supposing \(A(z) \coloneqq 1 + a_1 z + a_2z^2 + \cdots\), a direct expansion gives \begin{align*} {1\over A(z)} &= {1\over 1 + \displaystyle\sum_{k\geq 1} a_k z^k }\\ &= 1 - \qty{\sum_{k\geq 1} a_k z^k} \ + \qty{\sum_{k\geq 1} a_k z^k}^2 \ - \qty{\sum_{k\geq 1} a_k z^k}^3 \ + \cdots \\ &= 1 - (A(z) - 1) + (A(z) - 1)^2 - (A(z) - 1)^3 + \cdots ,\end{align*} where to compute the \(z^m\) term you only need to consider the first \(m+1\) summands in this expansion.
Purely formally, we have \begin{align*} {1\over A(z)} = {1 \over 1- (1-A(z))} = \sum_{k\geq 0} (1-A(z))^k z^k .\end{align*}
In order to invert \(A\) using this method, you need to clear powers of \(z\) so that a leading term is constant.
Invert \(\sin(z)\) using a geometric series, heeding the warning above.
Just a computation: \begin{align*} {1\over \sin(z)} &= {1\over z-{z^3\over 3!} + {z^5\over 5!} - { \mathsf{O}} (z^7) } \\ &={1\over z\qty{ 1 - {z^2\over 3!} + {z^4 \over 5!} - { \mathsf{O}} (z^6)} } \\ &= z^{-1}\qty{1\over 1 - p(z)} \qquad p(z) \coloneqq{z^2\over 3!} - {z^4\over 5!} + { \mathsf{O}} (z^6) \\ &= z^{-1}\sum_{k\geq 0} p(z)^k \\ &= z^{-1}\qty{ 1 + p(z) + p(z)^2 + { \mathsf{O}} (z^2)^3 } \\ &= z^{-1}\qty{ 1 \ + \qty{{z^2\over 3!} - {z^4\over 5!} + { \mathsf{O}} (z^6)} \ + \qty{{z^2\over 3!} - {z^4\over 5!} + { \mathsf{O}} (z^6)}^2 \ + { \mathsf{O}} (z^6)} \\ &= {1\over z}\qty{ 1 + {1\over 3!}z^2 + \qty{\qty{1\over 3!}^2 - {1\over 5!} }z^4 + { \mathsf{O}} (z^6) }\\ &= {1\over z} + {1\over 6}z + {7\over 360}z^3 + { \mathsf{O}} (z^5) .\end{align*}
Laurent expand \(\tan(z)\) at \(0\) using this method to compute \(1/\cos(z)\) and taking the product \(\sin(z) \cdot {1\over \cos(z)}\).

Polynomial Long Division
With practice, it’s much quicker to just do polynomial long division: \begin{align*} {1\over \sin(z) } = z^{-1}\qty{z\over \sin(z)} .\end{align*}
Now just run the grade school algorithm: \begin{align*} \begin{array}{rl} \underline{\hspace{8em} 1 + {1\over 3!}z^2 + \left({1\over 3!3!} - {1\over 5!} \right)z^4 + \cdots } & \\[-5pt] z-{1\over 3!}z^3 + {1\over 5!}z^5 + \cdots\hspace{3em} |z\hspace{9em} \\ \underline{-(z-{1\over 3!}z^3 + {1\over 5!}z^5 + \cdots)} & \\ {1\over 3!}z^3 - {1\over 5!}z^5 + {1\over 7!}z^7 - \cdots \hspace{0em}& \\ \underline{-{1\over 3!}z^2(z-{1\over 3!}z^3 + {1\over 5!}z^5 + \cdots)} & \\ \left( -{1\over 5!} + {1\over 3!3!}\right)z^5 + \left( {1\over 7!} - {1\over 3! 5!} \right)z + \cdots & \\ \end{array} .\end{align*}
Conclusion: \begin{align*} {z\over \sin(z)} = 1 + {z^2\over 3!} + {7 z^4 \over 360 } + { \mathsf{O}} (z^6) \\ \implies {1 \over \sin(z)} = {1\over z} + {z\over 3!} + {7 z^3 \over 360 } + { \mathsf{O}} (z^5) .\end{align*}
Polynomial long division basically works for formal power series, and with practice it’s fast enough to just do in your head. Recall the Euclidean algorithm, e.g. for \({z^3+1 \over z+1}\): \begin{align*} z^3 + 1 &= (z+1)(z^2) + (-z^2 + 1) \\ \ -z^2 + 1 &= (z+1)(-z) + (z+1) \\ (z+1) &= (z+1)(1) + 0 \\ \implies {z^3 + 1\over z+1} &= z^2 - z + 1 .\end{align*} This goes by increasing powers, but one can also go by decreasing powers: \begin{align*} 1+z^3 &= (1+z)(1) + (-z+z^3) \\ \ -z+z^3 &= (1+z)(-z) + (z^2 + z^3) \\ z^2 +z^3 &= (1+z)(z^2) + 0 \\ \implies {z^3 + 1\over z+1}&= 1 - z + z^2 ,\end{align*} which is useful for generating the first few low order terms of a series expansion.
Find a Laurent expansion about \(z_0=0\) for \(f(z) = \tan(z)\) by using polynomial long division on the series expansions for \(\sin(z)\) and \(\cos(z)\).
Computing the Laurent series for \(\tan(z)\) at \(z=0\):
\begin{align*} {\sin(z) \over \cos(z)} &= {z - {1\over 3!}z^3 + {1\over 5!} z^5 + { \mathsf{O}} (z^7) \over 1 - {1\over 2!} z^2 + {1\over 4!}z^4 + { \mathsf{O}} (z^6) } \\ \\ z - {1\over 3!}z^3 + {1\over 5!}z^5 &= \qty{1 - {1\over 2!}z^2 + {1\over 4!}z^4}(z) \ +\qty{ \qty{{1\over 2!} - {1\over 3!}}z^3 + \qty{-{1\over 4!} + {1\over 5!} }z^5 } \\ &= \qty{1 - {1\over 2!}z^2 + {1\over 4!}z^4}(z) \ +\qty{ {1\over 3}z^3 -{1\over 30}z^5 } \\ \\ {1\over 3}z^3 -{1\over 30}z^5 &= \qty{1 - {1\over 2!}z^2 + {1\over 4!}z^4}\qty{{1\over 3} z^3} \ +\qty{ \qty{ {1\over 6} - {1\over 30} } z^5 + \qty{ -{1\over 3\cdot 24} }z^7 } \\ &= \qty{1 - {1\over 2!}z^2 + {1\over 4!}z^4}\qty{{1\over 3} z^3} \ + \qty{ {2\over 15}z^5 - {1\over 72}z^7 } \\ \\ { {2\over 15}z^5 - {1\over 72}z^7 } &= \qty{1 - {1\over 2!}z^2 + {1\over 4!}z^4}\qty{{2\over 15} z^5} + \cdot \\ \\ \implies \tan(z) &= z + {1\over 3}z^3 + {2\over 15 }z^5 + { \mathsf{O}} (z^7) .\end{align*}