Series: Exercises

Write $S_N(z) \coloneqq\sum_{0\leq k\leq N} c_k (z-z_0)^k$ and $S \coloneqq\lim_{N\to\infty} S_N$. Suppose $R\coloneqq\qty{\limsup_k {\left\lvert {c_k} \right\rvert}^{1\over k} }^{-1}$ is the radius of convergence and let $r\leq R$, we’ll show $S_N\to S$ uniformly on any disc ${\left\lvert {z-z_0} \right\rvert}< r$.

Use the $M{\hbox{-}}$test: $\sum f_k$ converges if ${\left\lVert {f_k} \right\rVert}_\infty\leq M_k$ where $\left\{{M_k}\right\}\in \ell^1({\mathbb{N}})$. Define $f_k \coloneqq c_k (z-z_0)^k$, then $$\begin{align*} {\left\lVert {f_k} \right\rVert}_\infty =\sup_{{\left\lvert {z-z_0} \right\rvert}\leq r} {\left\lvert {c_k(z-z_0)^k} \right\rvert} \leq {\left\lvert {c_k} \right\rvert} r^k \coloneqq M_k .\end{align*}$$ Then $$\begin{align*} \sum_{k\geq 0} M_k = \sum_{k\geq 0} {\left\lvert {c_k} \right\rvert} r^k ,\end{align*}$$ and the claim is that this converges.

Note that since $r\leq R$, we have convergence of $$\begin{align*} \sum_{k\geq 0} c_k r^k .\end{align*}$$ Recall that root test: $$\begin{align*} \sum_k a_k \text{ converges absolutely if } \limsup_k {\left\lvert {a_k} \right\rvert}^{1\over k} < 1 .\end{align*}$$ Here we take $a_k \coloneqq c_k r^k$, then $$\begin{align*} \limsup_k {\left\lvert {a_k} \right\rvert}^{1\over k} &\coloneqq\limsup_k {\left\lvert {c_k r^k} \right\rvert}^{1\over k} \\ &= \limsup_k {\left\lvert {c_k} \right\rvert}^{1\over k} r \\ &< \limsup_k {\left\lvert {c_k} \right\rvert}^{1\over k} R\\ &\coloneqq\limsup_k {\left\lvert {c_k} \right\rvert}^{1\over k} \qty{\limsup_{k} {\left\lvert {c_k} \right\rvert}^{1\over k} }^{-1}\\ &= 1 ,\end{align*}$$ so $\sum_k {\left\lvert {c_k r^k} \right\rvert} < \infty$. Thus $\left\{{M_k}\right\}\in \ell^1({\mathbb{N}})$, and so $\sum_k f_k$ converges uniformly and absolutely on ${\left\lvert {z-z_0} \right\rvert} = r < R$.

Let $f(z) = \lim_{N\to\infty} \sum_{k\leq N} c_k (z-z_0)^k$. Use that power series converge uniformly and absolutely within their disc of convergence, each term is a continuous function, and finite sums of continuous functions are again continuous. So the partial sums $S_N$ are continuous, and since $S_N\to f$ uniformly, $f$ is continuous by the uniform limit theorem.

That $f$ is continuous is a local question: fixing a point $z_0$, take a closed disc ${\mathbb{D}}+z_0$ about $z_0$. By local uniform convergence $f_k\to f$ uniformly on ${\mathbb{D}}+z_0$, and differentiable $\implies$ continuous. So each $f_k$ is continuous, making $f$ continuous on ${\mathbb{D}}+z_0$ by the uniform limit theorem.

That $f$ is differentiable is again a local question: fix $z$ and write $\gamma \coloneqq\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}+ z\mkern-1.5mu}\mkern 1.5mu$ as the boundary of the disc about $z$. Define $g_k(\xi) \coloneqq{f_k\over \xi-z}$, so $g_k \to {f \over \xi-a}$ locally uniformly. Now apply Cauchy’s integral formula at $z$: $$\begin{align*} f(z) &= \lim_k f_k(z) \\ &= \lim_k {1\over 2\pi i}\int_\gamma {f_k(\xi) \over \xi - z}\,d\xi\\ &= \lim_k {1\over 2\pi i}\int_\gamma g_k(\xi)\,d\xi\\ &= {1\over 2\pi i}\int_\gamma \lim_k g_k(\xi)\,d\xi\\ &= {1\over 2\pi i}\int_\gamma g(\xi)\,d\xi\\ &= {1\over 2\pi i}\int_\gamma {f(\xi) \over \xi - z} \,d\xi ,\end{align*}$$ where we’ve used uniform convergence on $\gamma$ to commute the limit and integral. So $f$ has an integral representation, making it differentiable.

That $f_k'\to f'$: $$\begin{align*} \lim_k f_k'(z) &= \lim_k {1\over 2\pi i}\int_\gamma {f_k(\xi) \over (\xi - z)^2 }\,d\xi\\ &= {1\over 2\pi i}\int_\gamma \lim_k {f_k(\xi) \over (\xi - z)^2}\,d\xi\\ &= {1\over 2\pi i}\int_\gamma {f(\xi) \over (\xi - z)^2}\,d\xi\\ &= f'(z) .\end{align*}$$

That the convergence is locally uniform: first consider what happens on an closed discs $K = D$ with $\gamma \coloneqq{{\partial}}{D}$. Then for $z\in D$, $$\begin{align*} {\left\lvert {f'(z) - f_k'(z) } \right\rvert} &= {\left\lvert {{1\over 2\pi i} \int_{\gamma} {f(\xi) - f_k(\xi) \over (\xi - z)^2}\,d\xi} \right\rvert}\\ &\leq {1\over 2\pi}\int_{\gamma} {{\left\lvert {f(\xi) - f_k(\xi) } \right\rvert} \over {\left\lvert {\xi - z} \right\rvert}^2} \,d\xi\\ &\leq {1\over 2\pi}\int_{\gamma } { \sup_{\xi \in \gamma} {\left\lvert {f(\xi) - f_k(\xi) } \right\rvert} \over r^2 } \,d\xi\\ &= {1\over 2\pi} { \sup_{\xi \in \gamma } {\left\lvert {f(\xi) - f_k(\xi) } \right\rvert} \over r^2} \cdot {2\pi r} \\ &= { \sup_{\xi \in \gamma } {\left\lvert {f(\xi) - f_k(\xi) } \right\rvert}}/r .\end{align*}$$ Since $\gamma$ is compact, using locally uniform convergence of $f_k\to f$, there exists an $n_0$ such that $n\geq n_0$ bounds this $\sup$ by ${\varepsilon}$. For $K$ arbitrary, cover $K$ by discs $D_z$ for every $z\in K$ and extract a finite cover $\left\{{D_{z_k}}\right\}_{k\leq N}$. Produce $n_0, n_1,\cdots, n_N$ as in the above argument, and take $n\coloneqq\max\left\{{n_k}\right\}_{k\leq N}$ to obtain uniform convergence on every $D_{z_k}$ and thus on $K$.

• $R = 1/\limsup {\left\lvert {a^k} \right\rvert}^{1\over k} = 1\over {\left\lvert {a} \right\rvert}$
• $R = 1/\limsup {\left\lvert {a^{k^2}} \right\rvert}^{1\over k} = 1/\limsup {\left\lvert {a} \right\rvert}^k$, so $R=\infty$ if ${\left\lvert {a} \right\rvert}< 1$, $R=0$ if ${\left\lvert {a} \right\rvert}<1$, and $R=1$ if ${\left\lvert {a} \right\rvert} = 1$.

Choose the principal branch of $\log$, so take a branch cut at ${\mathbb{R}}_{\leq 0}$, to define $z^{1\over 2} = e^{{1\over 2}\log(z)}$. The radius of convergence is the distance to the nearest singularity or branch cut, so note that $f(z) = z^{1\over 2}$ is singular at $z=0$, so we compute ${\left\lvert {z_0 - 0} \right\rvert} = {\left\lvert {4+3i} \right\rvert} = 5$. The distance to the branch is also 5, so $R=5$.

For $z_1$, the distance to zero is ${\left\lvert {4+3i - 0} \right\rvert} = 5$ but the distance to the branch is 4, so $R=4$.

Note the subtle distinction: the series converges to $f$ in a disc ${\left\lvert {z-z_0} \right\rvert}<1$, but the series itself converges in larger discs.

Break this up into a principal part at $z=0$ and a holomorphic part: $$\begin{align*} f(z) = f_1(z) + f_2(z) \coloneqq\sum_{k\geq 1} 2^{-k}z^{-k} + \sum_{k\geq 0} 2^{-k}z^k .\end{align*}$$

Using the ratio test: $$\begin{align*} f_1(z) < \infty &\impliedby \limsup_k {\left\lvert {2^{-k}z^{-k}} \right\rvert}^{1\over k} < 1 \iff \limsup_k {\left\lvert {1\over 2z} \right\rvert} < 1 \iff {1\over 2}< {\left\lvert {z} \right\rvert} \\ f_2(z) < \infty &\impliedby \limsup_k {\left\lvert {2^{-k}z^{k}} \right\rvert}^{1\over k} < 1 \iff \limsup_k {\left\lvert {z\over 2} \right\rvert}< 1 \iff {\left\lvert {z} \right\rvert} < 2 .\end{align*}$$

So $f$ converges on ${1\over 2}< {\left\lvert {z} \right\rvert} < 2$.

$$\begin{align*} {1\over z(z-1)} = -{1\over z}{1 \over 1-z} = -{1\over z}\sum z^k .\end{align*}$$ and $$\begin{align*} {1\over z(z-1)} = {1\over z^2(1 - {1\over z})} = {1\over z^2} \sum \qty{1\over z}^k .\end{align*}$$

Note: once you see that everything is in terms of powers of $(z-z_0)$, you’re essentially done. For $z=0$: $$\begin{align*} {z+1 \over z(z-1)} &= {1\over z} {z+1 \over z-1} \\ &= -{z+1\over z} {1\over 1-z} \\ &= -\qty{1 + {1\over z}}\sum_{k\geq 0} z^k .\end{align*}$$

For $z=1$: $$\begin{align*} {z+1 \over z(z-1)} &= {1\over z-1}\qty{1 + {1\over z} } \\ &= {1\over z-1}\qty{1 + {1\over 1 - (1-z)} } \\ &= {1\over z-1} \qty{1 + \sum_{k\geq 0} (1-z)^k } \\ &= {1\over z-1} \qty{1 + \sum_{k\geq 0} (-1)^k (z-1)^k } .\end{align*}$$

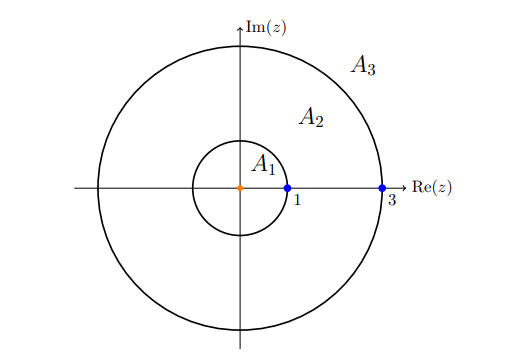
The three regions are

• $0 \leq {\left\lvert {z} \right\rvert} < 1$
• $1 < {\left\lvert {z} \right\rvert} < 3$
• $3 < {\left\lvert {z} \right\rvert} < \infty$

Write $f$ in terms of its principal parts at $z=1$ and $z=3$ by computing the residues:

• $\mathop{\mathrm{Res}}_{z=1}f(z) = (z-1)f(z)\Big|_{z=1} = {1\over z-3}\Big|_{z=1} = -{1\over 2}$
• $\mathop{\mathrm{Res}}_{z=3}f(z) = (z-3)f(z)\Big|_{z=3} = {1\over z-1}\Big|_{z=3} = {1\over 2}$

Thus $$\begin{align*} f(z) = {-1/2 \over z-1} + {1/2 \over z-3} .\end{align*}$$

Now find the two expansions for each term:

$$\begin{align*} {-1/2 \over z-1} &= {1/2 \over 1-z} = {1\over 2}\sum_{k\geq 0} z^k && 0 < {\left\lvert {z} \right\rvert} < 1 \\ {-1/2 \over z-1} &= -{1\over 2}{z^{-1}\over z^{-1}- 1} = -{1\over 2z}{1\over 1-z^{-1}} = -{1\over 2}\sum_{k\geq 0}z^{-k-1} && 1 < {\left\lvert {z} \right\rvert} < \infty \\ {1/2\over z-3} &= -{1\over 2}{1\over 3-z} = -{1\over 6}{1\over 1-{z\over 3}} = -{1\over 6}\sum_{k\geq 0}3^{-k} z^k && 0 < {\left\lvert {z} \right\rvert} < 3 \\ {1/2\over z-3} &= {1\over 2z}{1\over 1-3z^{-1}} = {1\over 2z} \sum_{k\geq 0}3^kz^{-k} = {1\over 2}\sum_{k\geq 0}3^k z^{-k-1} && 3 < {\left\lvert {z} \right\rvert} < \infty .\end{align*}$$

Now, just combinatorics to pick the various series that converge on the desired regions: $$\begin{align*} 0 \leq {\left\lvert {z} \right\rvert} < 1 \qquad & f(z) = {1\over 2}\sum_{k\geq 0}z^k - {1\over 6}\sum_{k\geq 0} 3^{-k}z^k \\ 1 \leq {\left\lvert {z} \right\rvert} < 3 \qquad & f(z) = -{1\over 2}\sum_{k\geq 0}z^{-k-1} - {1\over 6}\sum_{k\geq 0} 3^{-k}z^k \\ 3 \leq {\left\lvert {z} \right\rvert} < \infty \qquad & f(z) = - {1\over 2}\sum_{k\geq 0}z^{-k-1} + {1\over 2}\sum_{k\geq 0} 3^{k}z^{-k-1} .\end{align*}$$

$$\begin{align*} f(z) = z^2\qty{ 1 + {1\over 2!}\qty{1\over 3z}^2 + {1\over 4!}\qty{1\over 3z}^4 } = z^2 + {1\over 2! \cdot 3^2} + {1\over 4! \cdot 3^4}z^{-2} + \cdots .\end{align*}$$

One way: polynomial long division. $$\begin{align*} {1\over e^z-1} &= {1\over z + {1\over 2}z^2 + {1\over 6}z^2 + \cdots } \\ &= {1\over z}\qty{1 - {1\over 2}z + \qty{-{1\over 6} + {1\over 4} }z^2 + \cdots } \\ &= z^{-1}- {1\over 2} + {1\over 12}z + { \mathsf{O}} (z^3) .\end{align*}$$ Alternatively, use geometric series. Note that something like ${1\over 1-e^z} = \sum_{k\geq 0} e^{kz}$ won’t converge, and won’t even be calculable since each $e^{kz}$ contributes a constant term! $$\begin{align*} {1\over e^z-1} &= {1\over z + {1\over 2}z^2 + {1\over 6}z^3 + \cdots } \\ &= {1\over z(1 + {1\over 2}z + {1\over 6}z^2 + \cdots) } \\ &= z^{-1}{1\over 1 + q(z) } \qquad q(z) \coloneqq{1\over 2}z + {1\over 6}z^2 + \cdots \\ &= z^{-1}\sum_{k\geq 0}(-q(z))^k \\ &= z^{-1}\qty{1 - q(z) + q(z)^2 - \cdots } \\ &= z^{-1}\qty{1 - \qty{{1\over 2}z + {1\over 6}z^2 + \cdots } + \qty{{1\over 2}z + {1\over 6}z^2 + \cdots }^2 - \cdots } \\ &= z^{-1}\qty{ 1 - {1\over 2} z + \qty{-{1\over 6} + \qty{1\over 2}^2 } z^2 + { \mathsf{O}} (z^3) } \\ &= z^{-1}- {1\over 2} + {1\over 12}z + { \mathsf{O}} (z^2) .\end{align*}$$

Note that a direct expansion won’t work, since there are infinitely many contributions to the constant term. Instead, a trick: consider $g(z) \coloneqq e^z\cos(z)$, so $g(1/z ) = f(z)$. Expanding $g$ is easier: $$\begin{align*} g(z) &= e^{z}\cos(z)\\ &= {1\over 2}e^z\qty{e^{iz} + e^{-iz}} \\ &= {1\over 2}\qty{e^{(1+i)z} + e^{(1-i)z}} \\ &= {1\over 2} \sum_{k\geq 0}\qty{(1+i)^k + (1-i)^k} {z^k\over k!} \\ \implies f(z) &= {1\over 2} \sum_{k\geq 0}\qty{(1+i)^k + (1-i)^k} {1 \over k!z^k } \\ .\end{align*}$$

Write $g(z) \coloneqq\cos(1-z)$, so $g(1/z) = f(z)$, and expand: $$\begin{align*} g(z) &= \cos(1-z) \\ &= {1\over 2}\qty{e^{i(1-z)} + e^{-i(1-z)}} \\ &= {1\over 2}\qty{e^i e^{-iz} + e^{-i} e^{iz}}\\ &= {1\over 2}\sum_{k\geq 0} \qty{ (-i)^k e^i + i^k e^{-i} } {z^k \over k!} \\ \implies f(z) &= {1\over 2}\sum_{k\geq 0} \qty{ ( (-i)^k e^i + i^k e^{-i} } {1 \over k!z^k} .\end{align*}$$

Taking $k=1$ yields $$\begin{align*} c_{-1} = {-ie^i + ie^{-i} \over 2} = -i\cdot {e^i - e^{-i}\over 2} = {e^i - e^{-i}\over 2i} = \sin(1) .\end{align*}$$

$$\begin{align*} f(z) = e^{-(1-z)} = e^{z-1} = e^{-1}e^z = e^{-1}\sum_{k\geq 0} {z^k\over k!} .\end{align*}$$ Since $e^z$ is entire, this converges on ${\mathbb{C}}$.

At $z=0$, we can use a geometric series approach since ${\left\lvert {e^z} \right\rvert} = e^{\Re(z)} \leq 1$ near $0$. However, we still have to get rid of the leading 1 in the expansion of $e^z$ in order to get a constant coefficient. $$\begin{align*} {1\over 1 + e^z} &= {1\over 1 + 1 + z + {1\over 2!}z^2 + {1\over 3!} z^3 + { \mathsf{O}} (z^4)} \\ &= {1\over 2 + z + {1\over 2!}z^2 + {1\over 3!} z^3 + { \mathsf{O}} (z^4) } \\ &= {1\over 2} {1\over 1 + {1\over 2} z + {1\over 2\cdot 2!}z^2 + {1\over 2\cdot 3!} z^3 + { \mathsf{O}} (z^4) } \\ &= {1\over 2}{1\over 1 - (-p(z)) } \qquad p(z) \coloneqq{1\over 2}z + {1\over 2\cdot 2!}z^2 + {1\over 2\cdot 3!}z^3 + { \mathsf{O}} (z^4) \\ &= {1\over 2} \sum_{k\geq 0} (-p(z))^k \\ &= {1\over 2}\Big[ 1 - \qty{{1\over 2}z + {1\over 2\cdot 2!}z^2 + {1\over 2\cdot 3!}z^3 + { \mathsf{O}} \qty{z^4} } \\ &\qquad + \qty{ {1\over 2}z + {1\over 2\cdot 2!}z^2 + {1\over 2\cdot 3!}z^3 + { \mathsf{O}} \qty{z^4} }^2 \\ &\qquad - \qty{{1\over 2} z + {1\over 2\cdot 2!}z^2 + {1\over 2\cdot 3!}z^3 + { \mathsf{O}} \qty{z^4} }^3 \\ &\qquad - { \mathsf{O}} (z^4) \Big]\\ &= {1\over 2} \Big[ 1 + z\qty{- {1\over 2}} + z^2\qty{- {1\over 2\cdot 2!} + \qty{1\over 2}^2}\\ &\qquad + z^3 \Big( -{1\over 2\cdot 3! } +\left[ \qty{1\over 2}^3 + {1\over 2}{1\over 2\cdot 2!}\right] - \qty{1\over 2}^3 \Big) \\ &\qquad + { \mathsf{O}} (z^4) \Big]\\ &= {1\over 2} - {1\over 4}z + 0z^2 + {1\over 48}z^3 + { \mathsf{O}} (z^4) .\end{align*}$$

Expanding at $z-i\pi$: quite a bit easier. Let $\omega \coloneqq z-i\pi$, then $$\begin{align*} {1\over 1 + e^z} &= {1\over 1 + e^{z-i\pi}e^{i\pi}} \\ &= {1\over 1 - e^{\omega} } \\ &= {1 \over -\omega - {1\over 2!}\omega^2 - {1\over 3!}\omega^3 - { \mathsf{O}} (\omega^4) } \\ &= -{1\over \omega} {1 \over 1 + {1\over 2!}\omega + {1\over 3!}\omega^2 + { \mathsf{O}} (\omega^3) } \\ &= -{1\over \omega}{1\over 1-(- p(z) ) } \qquad p(z) \coloneqq\sum_{k\geq 2}{\omega^{k-1}\over k!} \\ &= -{1\over \omega} \sum_{k\geq 0} (-p(z))^k \\ &= -{1\over \omega} \left[ 1 - \qty{{1\over 2!}\omega + {1\over 3!}\omega^2 + { \mathsf{O}} (\omega^3)} + \qty{{1\over 2!}\omega + {1\over 3!}\omega^2 + { \mathsf{O}} (\omega^3)}^2 - { \mathsf{O}} (\omega^3) \right] \\ &= -{1\over \omega} \left[ 1 + \omega\qty{-{1\over 2!}} + \omega^2\qty{-{1\over 3!} + \qty{1\over 2!}^2} + { \mathsf{O}} (\omega^3) \right] \\ &= -{1\over w} + {1\over 2} - {1\over 12}\omega + { \mathsf{O}} (\omega^2) .\end{align*}$$