Complex Preliminaries

Since \({\mathbb{C}}\) is a field, \({\mathbb{C}}[x]\) is a UFD.

Derivation of complex \(n\)th roots of a complex number \(z\): \begin{align*} z = re^{i\theta} = re^{i\qty{\theta + 2k\pi}} \implies z^{1/n} = \qty{ re^{i\qty{\theta + 2k\pi}} }^{1\over n} = r^{1\over n} e^{i\qty{\theta + 2k\pi \over n}} \leadsto \left\{{ \omega_k \coloneqq r^{1/n} e^{i \qty{ \theta + 2k\pi \over n} } {~\mathrel{\Big\vert}~}0 \leq k \leq n-1 }\right\} .\end{align*} Note that one root is \(r^{1/n}\in {\mathbb{R}}\), and the rest are separated by angles of \(2\pi/n\).

For \(f\) a quadratic, writing \(\Delta \coloneqq b^2-4ac\), the roots take on the form \begin{align*} z_k = {1\over 2a}\qty{-b + i\sqrt{-\Delta}} = {1\over 2a}\qty{-b + i\sqrt{4ac - b^2}} .\end{align*} For monic polynomials, this becomes slightly nicer: \begin{align*} z_k = {1\over 2}\qty{-b + i\sqrt{4c-b^2} } .\end{align*}

\begin{align*} z^n-1 &= \prod_{k=0}^{n-1} (z-\zeta_n^k) = (z-1)(z-\zeta_n)(z-\zeta_n^2)\cdots(z-\zeta_n^{n-1}) && \zeta_n \coloneqq e^{2\pi i \over n} .\end{align*}

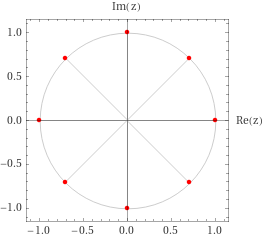
What the roots look like:

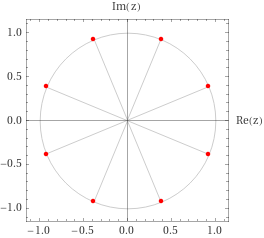
• \(n\) odd:

• \(n\) even: \(\theta_0=0\), increment by \(2\pi/n\). Always have \(\pm 1\).

Write \(w=Re^{i\theta}\), then \begin{align*} z^n = w \implies z = R^{1\over n}e^{i(\theta + 2k\pi )\over n} = R^{1\over n}e^{i\theta\over n}e^{2\pi i k \over n} = \qty{Re^{i\theta}}^{1\over n}\zeta_n^k .\end{align*} Thus setting \(w_0 \coloneqq(Re^{i\theta})^{1\over n}\) yields \begin{align*} z^n - w = \prod_{k=0}^{n-1} (z-w_0\zeta_n^k) = (z-w_0)(z-w_0\zeta_n)\cdots (z-w_0\zeta_n^{n-1}) .\end{align*}

Factoring \(z^n+1\): write \(1 = e^{i\pi}\) to get \(w_0 \coloneqq e^{i\pi \over n}\), then \begin{align*} z^n+1 = \prod_{k=0}^{n-1}(z-w_0\zeta_k) &= (z-e^{i\pi \over n}e^{2i\pi \over n}) (z-e^{i\pi \over n}e^{4i\pi \over n}) \cdots (z-e^{i\pi \over n}e^{2(n-1)i \pi \over n}) \\ &= (z - e^{3i\pi \over n})(z-e^{5i\pi \over n}) \cdots (z - e^{(2n-1)i\pi \over n}) .\end{align*}

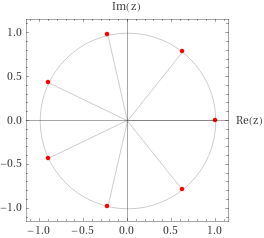
What the roots look like:

• \(n\) odd: start at \(\theta_0 = \pi\), increment by \(2\pi/n\).

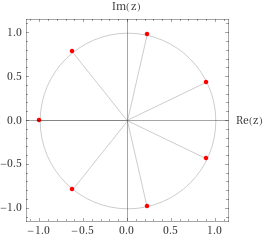
• \(n\) even: start at \(\theta_0 = \pi/n\), increment by \(2\pi/n\).