If \(f\) is continuous on a domain \(\Omega\) and \(\int_T f = 0\) for every triangle \(T\subset \Omega\), then \(f\) is holomorphic.
Fix \(z_0\in \Omega\) and attempt to define a primitive \(F(z) \coloneqq\int_{z_0}^z f(\xi) \,d\xi\), integrating along any path connecting \(z_0\) to \(z\). This will be well-defined since integrating along 2 different paths \(\gamma, \mu\) will yield \(\int_\gamma f + \int_\mu f = \int_{\gamma \cdot \mu} f = 0\) by assumption since it bounds a closed region. Then just show \(F' = f\).
If every integral along a triangle vanishes, implies holomorphic. Equivalently, \(f(z)\,dz\) is a closed differential form iff \(f\) is holomorphic.
Sometimes stated for rectangles with sides parallel to axes. The power of this theorem is that virtually no assumptions on \(f\) are made, e.g. \(f\) is not even assumed smooth or even differentiable.
If \(\left\{{ f_n }\right\}_{n\in {\mathbb{N}}}\) is a holomorphic sequence on a region \(\Omega\) which uniformly converges to \(f\) on every compact subset \(K \subseteq \Omega\), then \(f\) is holomorphic, and \(f_n' \to f'\) uniformly on every such compact subset \(K\).
Commute limit with integral and apply Morera’s theorem.
This can be applied to series of the form \(\sum_k f_k(z)\).
Holomorphic implies analytic.
Taken from Gamelin: the proof is based on Morera’s theorem. Idea: break region into nested cubes:
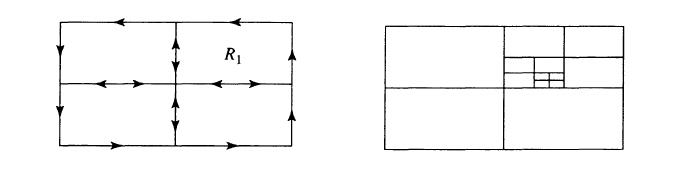
Let \(R\) be a closed rectangle in \(D\). We subdivide \(R\) into four equal subrectangles. Since the integral of \(f(z)\) around \(\partial R\) is the sum of the integrals of \(f(z)\) around the four subrectangles, there is at least one of the subrectangles, call it \(R_{1}\), for which \begin{align*} \left|\int_{\partial R_{1}} f(z) d z\right| \geq \frac{1}{4}\left|\int_{\partial R} f(z) d z\right| \end{align*} Now subdivide \(R_{1}\) into four equal subrectangles and repeat the procedure. This yields a nested sequence of rectangles \(\left\{R_{n}\right\}\) such that \begin{align*} \left|\int_{\partial R_{n}} f(z) d z\right| \geq \frac{1}{4}\left|\int_{\partial R_{n-1}} f(z) d z\right| \geq \cdots \geq \frac{1}{4^{n}}\left|\int_{\partial R} f(z) d z\right| . \end{align*} Since the \(R_{n}\) ’s are decreasing and have diameters tending to 0 , the \(R_{n}\) ’s converge to some point \(z_{0} \in D\). Since \(f(z)\) is differentiable at \(z_{0}\), we have an estimate of the form \begin{align*} \left|\frac{f(z)-f\left(z_{0}\right)}{z-z_{0}}-f^{\prime}\left(z_{0}\right)\right| \leq \varepsilon_{n}, \quad z \in R_{n}, \end{align*} where \(\varepsilon_{n} \rightarrow 0\) as \(n \rightarrow \infty\). Let \(L\) be the length of \(\partial R\). Then the length of \(\partial R_{n}\) is \(L / 2^{n}\). For \(z\) belonging to \(R_{n}\) we have the estimate \begin{align*} \left|f(z)-f\left(z_{0}\right)-f^{\prime}\left(z_{0}\right)\left(z-z_{0}\right)\right| \leq \varepsilon_{n}\left|z-z_{0}\right| \leq 2 \varepsilon_{n} L / 2^{n} . \end{align*} From the \(M L\)-estimate and Cauchy’s theorem, we obtain \begin{align*} \begin{aligned} \left|\int_{\partial R_{n}} f(z) d z\right| &=\left|\int_{\partial R_{n}}\left[f(z)-f\left(z_{0}\right)-f^{\prime}\left(z_{0}\right)\left(z-z_{0}\right)\right] d z\right| \\ & \leq\left(2 \varepsilon_{n} L / 2^{n}\right) \cdot\left(L / 2^{n}\right)=2 L^{2} \varepsilon_{n} / 4^{n} \end{aligned} \end{align*} Hence \begin{align*} \left|\int_{\partial R} f(z) d z\right| \leq 4^{n}\left|\int_{\partial R_{n}} f(z) d z\right| \leq 2 L^{2} \varepsilon_{n} \end{align*} Since \(\varepsilon_{n} \rightarrow 0\) as \(n \rightarrow \infty\), we must have \begin{align*} \int_{\partial R} f(z) d z=0 . \end{align*} By Morera’s theorem, \(f(z)\) is analytic.
Exercises
For \(\Omega\subseteq{\mathbb{C}}\), show that \(A({\mathbb{C}})\coloneqq\left\{{f: \Omega \to {\mathbb{C}}{~\mathrel{\Big\vert}~}f\text{ is holomorphic, bounded}}\right\}\) is a Banach space.
Hint: Apply Morera’s Theorem and Cauchy’s Theorem