Strategies
Some resources:
-
For guidelines for what techniques to use, see this very detailed note.
-
Some good computations here.
-
The reverse triangle shows up here often! \begin{align*} {\left\lvert {z-w} \right\rvert} \geq {\left\lvert { {\left\lvert {z} \right\rvert} - {\left\lvert {w} \right\rvert}} \right\rvert} \implies {1\over {\left\lvert {z-w} \right\rvert}}\leq {\left\lvert {1\over {\left\lvert {z} \right\rvert} - {\left\lvert {w} \right\rvert}} \right\rvert} \\ {\left\lvert {z+w} \right\rvert} = {\left\lvert {z -(-w)} \right\rvert} \geq {\left\lvert { {\left\lvert {z} \right\rvert} - {\left\lvert {w} \right\rvert}} \right\rvert} \implies {1\over {\left\lvert {z+w} \right\rvert}}\leq {\left\lvert {1\over {\left\lvert {z} \right\rvert} - {\left\lvert {w} \right\rvert}} \right\rvert} \\ .\end{align*}
-
Also often useful: \(e^{-x}\) is monotonically decreasing on \({\mathbb{R}}\), so \begin{align*} a\leq b \implies e^{-a} \geq e^{-b} .\end{align*}
-
All residue theorems assume counterclockwise orientation. If your curve is clockwise (e.g. in the lower half-plane), so it traces out \([-R, R]\) on \({\mathbb{R}}\)), then a negative sign is introduced.
-
Some standard contours:
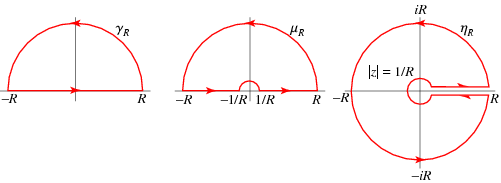
Let \(\deg\) denote the \(z{\hbox{-}}\)adic valuation, so \(\deg(p(x)/q(x)) = \deg(p) - \deg(q)\).
For \(\int_{\mathbb{R}}f\): Semicircle. Always get \begin{align*} \int_{\mathbb{R}}f = \sum_{z_0\in {\mathbb{H}}} \mathop{\mathrm{Res}}_{z=z_0}f(z) .\end{align*}

For \(\int_{{\mathbb{R}}_{\geq 0}} f\): use symmetry to convert to \(\int_{\mathbb{R}}\) (e.g. if \(f\) is even), or find a symmetric ray and use a sector:


Semicircles. Realize \begin{align*} \int_{\mathbb{R}}f(z)\cos(z) = \Re\qty{\int_{\mathbb{R}}f(z)e^{iz}} .\end{align*}
This works for \(f(z)e^{iz}\) where \(f(z) = p(z)/q(z)\) with \(\deg q \geq \deg p+2\) by the ML estimate, or \(\deg q \geq \deg p +1\) by Jordan’s lemma.
Set \(z=e^{i\theta}\), then \begin{align*} 2\cos(z) = z + z^{-1}, \quad 2i\sin(z) = z - z^{-1}, && \,d\theta= {\,dz\over iz} .\end{align*} Then \(\int_{-\pi}^\pi f(\theta)\,d\theta\to \int_{{\left\lvert {z} \right\rvert} = 1} f(z) \,dz\), which reduces to a residue count in \({\mathbb{D}}\).
If \(f(z) \approx \cos(z), \sin(z), \tan(z), \cdots\): check if \(\displaystyle\int f \approx \Re\displaystyle\int (g(e^{iz}))\).
-
\(\int_{{\mathbb{R}}_{\geq 0}} f(x)x^\alpha\) for \(\alpha\) rational with \({\left\lvert {\alpha} \right\rvert} < 1\)
-
For \(f\) rational with \(\deg f\leq -2\), take a keyhole
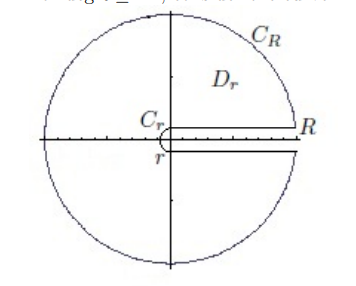
-
A useful fact: \begin{align*} \lim_{{\varepsilon}\searrow 0} \ln(x-i{\varepsilon}) = \ln(x) + 2\pi i .\end{align*}
-
Another useful fact: for any constant \(c\), \begin{align*} \lim_{x\to 0} {x\ln(x) \over x^n + c} = 0 .\end{align*} Note that you can’t drop the constant!
-
-
\(\int_{{\mathbb{R}}_{\geq 0}} f(x) \log(x)\): indented semicircular contours
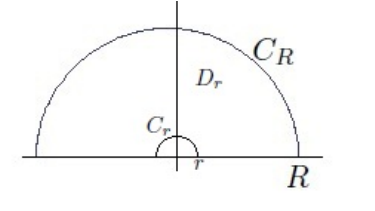
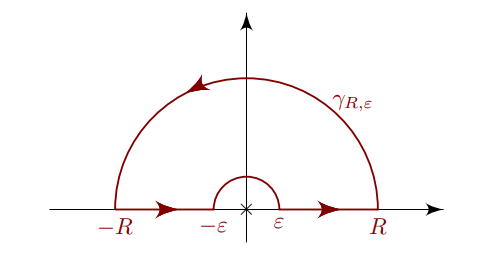
- When a log trick is useful: if \(f(z) = \log(z)g(z)\) where \(\int g(z)\) is easy, try a contour that is a rotation of \({\mathbb{R}}\). The substitution usually yields \(\log(\zeta x) \leadsto \ln{\left\lvert {x} \right\rvert} + i\theta\), so \(\int \log(\zeta x)g(\zeta x) = \int \log(x)g(x) + \int i\theta g(x)\) if \(g\) is \(\zeta{\hbox{-}}\)invariant.
The replication trick: if \(f(z) = f(\zeta_m z)\) for some \(m\), try a sector. If \(f(z) = f(z + ib)\) for some \(b\), a rectangle.
For real integrals: \begin{align*} \operatorname{PV} \int_{-\infty}^{\infty} \frac{f(x)}{x-x_{0}} d x=\lim _{\epsilon \backslash 0}\left(\int_{-\infty}^{x_{0}-\epsilon} f(x) d x+\int_{x_{0}+\epsilon}^{\infty} f(x) d x\right) . .\end{align*} The same principle works for complex contours, e.g. for \(\int_{\mathbb{R}}p(z)/q(z)\) where \(q\) has real roots:
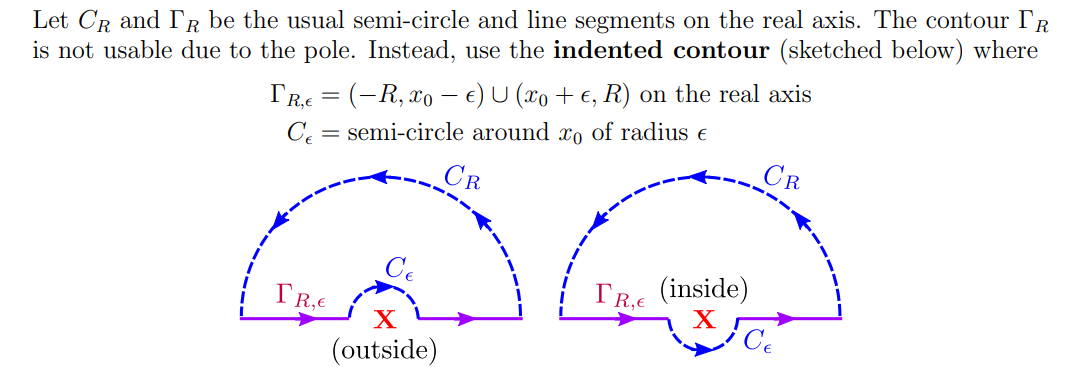
The contours along the real line converge to the principal values of the real integral.
The ML Estimate
\begin{align*} {\left\lvert { \int_\gamma f(z) \,dz} \right\rvert} \leq ML \coloneqq\sup_{\xi \in \gamma} {\left\lvert {f(\xi)} \right\rvert} \cdot \mathop{\mathrm{length}}(\gamma) .\end{align*}
If \(C_R\) is a semicircular contour subtending an angle of \(\theta\), \begin{align*} {\left\lvert {\int_{C_R} f\, } \right\rvert}\leq MR\theta ,\end{align*} so provided \(M = { \mathsf{O}} \qty{1\over R^{1+{\varepsilon}}}\), this goes to zero as \(R\to\infty\). If \(M = { \mathsf{O}} (R)\), use Jordan’s lemma!
\begin{align*} {\left\lvert { \int_\gamma f(z) \,dz} \right\rvert} &\leq \int_\gamma {\left\lvert {f(z)} \right\rvert} \,dz\\ &\leq \int_\gamma \sup_{\xi\in \gamma} {\left\lvert {f(\xi)} \right\rvert} \,dz\\ &\coloneqq\int_\gamma M\,dz\\ &= M \cdot \mathop{\mathrm{length}}(\gamma) .\end{align*}
Jordan’s Lemma
For \(\alpha > 0\), define \begin{align*} C_R \coloneqq\left\{{ z=Re^{it} {~\mathrel{\Big\vert}~}t\in [0, \pi] }\right\} .\end{align*}
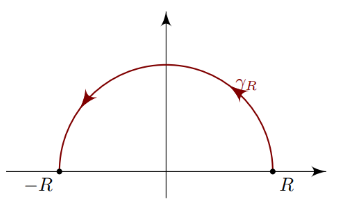 \begin{align*}
{\left\lvert {\int_{C_R} e^{i\alpha z} g(z) \,dz} \right\rvert} \leq \pi\alpha^{-1}M_R \qquad M_R \coloneqq\sup_{z\in C_R} {\left\lvert {g(z)} \right\rvert}
.\end{align*}
Note that if \(M_R\to 0\) as \(R\to \infty\), this integral vanishes – so this works if \(M_R \in { \mathsf{O}} \qty{1\over R^{\varepsilon}}\) for \({\varepsilon}>0\).
\begin{align*}
{\left\lvert {\int_{C_R} e^{i\alpha z} g(z) \,dz} \right\rvert} \leq \pi\alpha^{-1}M_R \qquad M_R \coloneqq\sup_{z\in C_R} {\left\lvert {g(z)} \right\rvert}
.\end{align*}
Note that if \(M_R\to 0\) as \(R\to \infty\), this integral vanishes – so this works if \(M_R \in { \mathsf{O}} \qty{1\over R^{\varepsilon}}\) for \({\varepsilon}>0\).
For \(\alpha < 0\), the same statement holds with the contour replaced by \(\tilde C_R\coloneqq\left\{{Re{it} {~\mathrel{\Big\vert}~}t\in [0, -\pi]}\right\}\). This is because the main estimate involves \begin{align*} \cdots & \leq \lim _{R \rightarrow \infty} \int_{H_{R}} e^{-\alpha R \sin \theta}|F(z)| R d \theta ,\end{align*} which goes to zero if \(-\alpha n\sin(\theta)<0\), i.e.
- \(\alpha>0\) and \(\sin(\theta)>0\), so \(C_R\) is in the upper half-plane, or
- \(\alpha < 0\) and \(\sin(\theta)<0\), so \(C_R\) is in the lower half-plane.
Compare to the above computation of \(\int_{\mathbb{R}}{ \cos(x) \over x^2 + 1}\). Taking \(\alpha = 1\), this yields \begin{align*} {\left\lvert { \int_{C_R} { e^{iz} \over z^2 + 1 } \,dz} \right\rvert} \leq \pi \sup_{z\in C_R} {\left\lvert {1\over z^2 +1} \right\rvert} \leq {\pi \over R^2 - 1}\to 0 .\end{align*}

The quick justification: \begin{align*} \lim _{R \rightarrow \infty}\left|\int_{H_{R}} e^{i m z} F(z) d z\right| &=\lim _{R \rightarrow \infty}\left|\int_{H_{R}} e^{i m R \cos \theta-m R \sin \theta} F(z) R e^{i \theta} d \theta\right| \\ & \leq \lim _{R \rightarrow \infty} \int_{H_{R}} e^{-m R \sin \theta}|F(z)| R d \theta .\end{align*}
\begin{align*} {\left\lvert { \int_{C_R} f(z)\,dz} \right\rvert} &= {\left\lvert { \int_{C_R} e^{iaz}g(z) \,dz} \right\rvert} \\ &= {\left\lvert { \int_{[0, \pi]} e^{ia\qty{Re^{it}}}g(Re^{it}) iRe^{it} \,dt} \right\rvert} \\ &\leq \int_{[0, \pi]} {\left\lvert { e^{ia\qty{Re^{it}}}g(Re^{it}) iRe^{it}} \right\rvert} \,dt\\ &=R \int_{[0, \pi]} {\left\lvert { e^{ia\qty{Re^{it}}}g(Re^{it})} \right\rvert} \,dt\\ &\leq R M_R \int_{[0, \pi]} {\left\lvert { e^{ia\qty{Re^{it}}}} \right\rvert} \,dt\\ &= R M_R \int_{[0, \pi]} e^{\Re\qty{iaRe^{it}}} \,dt\\ &= R M_R \int_{[0, \pi]} e^{\Re\qty{iaR\qty{\cos(t) + i\sin(t) } }} \,dt\\ &= R M_R \int_{[0, \pi]} e^{-aR\sin(t) } \,dt\\ &= 2 R M_R \int_{[0, \pi/2]} e^{-aR\sin(t) } \,dt\\ &\leq 2R M_R \int_{[0, \pi/2]} e^{-aR\qty{2t\over \pi} } \,dt\\ &= 2RM_R \qty{\pi \over 2aR}\qty{1-e^{-aR}} \\ &= {\pi M_R \over a} .\end{align*}
where we’ve used that on \([0, \pi/2]\), there is an inequality \(2t/\pi \leq \sin(t)\). This is obvious from a picture, since \(\sin(t)\) is a height on \(S^1\) and \(2t/\pi\) is a height on a diagonal line:

Exercises
Use a semicircular contour and the residue theorem to evaluate \begin{align*} I = \int_{\mathbb{R}}{\cos(x) \over x^2 + 1 }\,dx .\end{align*}
Write \begin{align*} I = \Im \int_{\mathbb{R}}f(z) \,dz&& f(z) \coloneqq{e^{iz} \over z^2 + 1}\,dz .\end{align*} Define contours \(C_1 = [-R, R]\), \(C_2 = \left\{{Re^{it} {~\mathrel{\Big\vert}~}t\in [0, \pi]}\right\}\), and \(\Gamma = C_1 + C_2\). Then noting that \(z_0 = i\) is the only pole of \(f\) in \({\mathbb{H}}\), by the residue theorem \begin{align*} \int_\Gamma f(z) \,dz= 2\pi i \mathop{\mathrm{Res}}_{z=i} f(z) = \qty{\int_{C_1} + \int_{C_2}} f .\end{align*} Note also that \begin{align*} I = \Re \lim_{R\to\infty} \int_{C_1} f .\end{align*}
By the ML estimate, \begin{align*} {\left\lvert {\int_{C_2} f(z)\,dz} \right\rvert} &\leq 2\pi R \sup_{z\in C_2} {\left\lvert {f(z)} \right\rvert} \\ &\coloneqq 2\pi R \sup_{z\in C_2} {\left\lvert {e^{iz}\over z^2 + 1} \right\rvert} \\ &\leq 2\pi R \sup_{z\in C_2} {1 \over {\left\lvert { z^2 + 1} \right\rvert} } \\ &\leq 2\pi R\sup_{z\in C_2} {1 \over {\left\lvert {z} \right\rvert}^2 - 1 } \text{ by the reverse triangle ineq.}\\ &= {2\pi R\over R^2-1} \\ &= { \mathsf{O}} (R^{-1}) \\ &\overset{R\to\infty}\longrightarrow 0 .\end{align*}
For the residue, \(z=i\) is at worst an order 1 pole, and remains order 1 since \(i\) is not a zero of the numerator. \begin{align*} \mathop{\mathrm{Res}}_{z=i} f(z) &= \mathop{\mathrm{Res}}_{z=i} {e^{iz} \over (z+i)(z-i)} \\ &= { e^{iz} \over z+i}\Big|_{z=i} \\ &= {1\over 2ei} .\end{align*} Thus \begin{align*} \lim_{R\to\infty}\int_{C_1} f = 2\pi i \mathop{\mathrm{Res}}_{z=i} f = {2\pi i \over 2ei} = {\pi \over e} \\ \implies I = \Re\qty{\pi \over e} = {\pi \over e} .\end{align*}
Note that this also shows that \begin{align*} \int_{\mathbb{R}}{ \sin(z) \over z^2 + 1} \,dz= 0 .\end{align*}
Compute \begin{align*} \int_{\mathbb{R}}{\sin(x) \over x}\,dx .\end{align*}
Note that the ML bound is not sufficient to bound a semicircular contour: \begin{align*} {\left\lvert {\int_{C_R} { e^{iz} \over z}\,dz} \right\rvert} \leq \pi R \sup_{z\in C_R} {\left\lvert {1\over z} \right\rvert} = \pi \not\to 0 .\end{align*} Jordan’s lemma on this contour yields \begin{align*} {\left\lvert {\int_{C_R} {e^{iz} \over z} \,dz} \right\rvert} \leq \pi \sup_{z\in C_R}{\left\lvert {1\over Z} \right\rvert} = {\pi \over R} \to 0 .\end{align*}
To compute the full integral, use an indented semicircular contour:
- \(C_+ \coloneqq[{\varepsilon}, R]\)
- \(C_i \coloneqq[-R, {\varepsilon}]\)
- \(C_{\varepsilon}\coloneqq{\varepsilon}e^{it}\) with \(t\in [0, \pi]\)
- \(C_R \coloneqq R e^{it}\) with \(t\in [0, \pi]\)
- \(\Gamma \coloneqq C_+ + C_R + C_- - C_{\varepsilon}\), noting that \(C_{\varepsilon}\) is is taken with a reversed orientation.
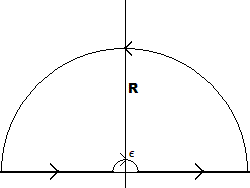
Write \(I\) for the original integral, and \begin{align*} f(z) \coloneqq{ e^{iz} \over z} \implies I = \Im \lim_{{\varepsilon}\to 0}\lim_{R\to \infty} \qty{\int_{C_-} + \int_{C_+}}f .\end{align*} By the residue theorem \begin{align*} \int_\gamma f(z) \,dz &= 2\pi i \sum_{z_k \in {\mathbb{H}}} \mathop{\mathrm{Res}}_{z=z_k} f(z) = 0 \\ &= \qty{\int_{C_+} + \int_{C_R} + \int_{C_-} - \int_{C_{\varepsilon}} }f \\ &= \tilde I + \qty{\int_{C_R} - \int_{C_{\varepsilon}}}f ,\end{align*} where \(\Im(\tilde I) = I\) is the original integral, so \begin{align*} \tilde I = -\qty{\int_{C_R} - \int_{C_{\varepsilon}}}f .\end{align*}
Since \(\int_{C_R}f \to 0\), it just remains to compute \(\int_{C_{\varepsilon}}\). By the fractional residue formula, \begin{align*} \lim_{{\varepsilon}\to 0} {e^{iz} \over z}\,dz= i\pi \mathop{\mathrm{Res}}_{z=0} {e^{iz} \over z} = i\pi .\end{align*} Thus \begin{align*} I = \Im(i\pi) = \pi .\end{align*}