A summary:
- \(z\mapsto -z\) is a reflection about \(y=x\), so for example sends \({\mathbb{H}}\to Q_{34}\) and \({\mathbb{D}}\cap{\mathbb{H}}\to {\mathbb{D}}\cap Q_{34}\) and vice-versa.
- \(z\mapsto 1/z\): write as \(Re^{it} \mapsto R^{-1}e^{-it}\), which is reflection about \({\mathbb{R}}\) and inversion through \(S^1\).
- \({\mathbb{D}}\to {\mathbb{D}}\): \(\lambda {z-a\over 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5muz}\) for rotations \(\lambda \in S^1\)
- \({\mathbb{H}}\to {\mathbb{D}}\): the Cayley map \(z\mapsto {z-i\over z+i}\)
-
Horizontal strips to \({\mathbb{H}}\): use \(z\mapsto e^z\) for \(0<\Im(z) < \pi \to {\mathbb{H}}\)
- These send \(\left\{{\Im(z) \in (-\pi, \pi) }\right\}\longrightarrow{\mathbb{C}}\setminus{\mathbb{R}}_{\leq 0}\).
-
Sectors to \({\mathbb{H}}\): for \(0<\operatorname{Arg}(z) < {\pi \over n}\), use \(z\mapsto z^{n}\) to get \({\mathbb{H}}\).
-
Some variants:
-
Unfolding a half-plane:
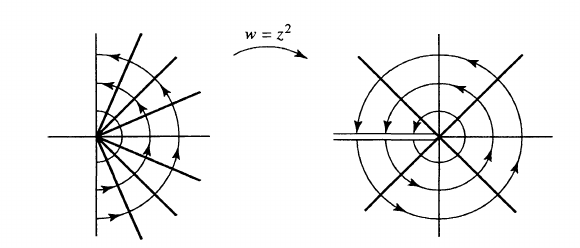 Generally,
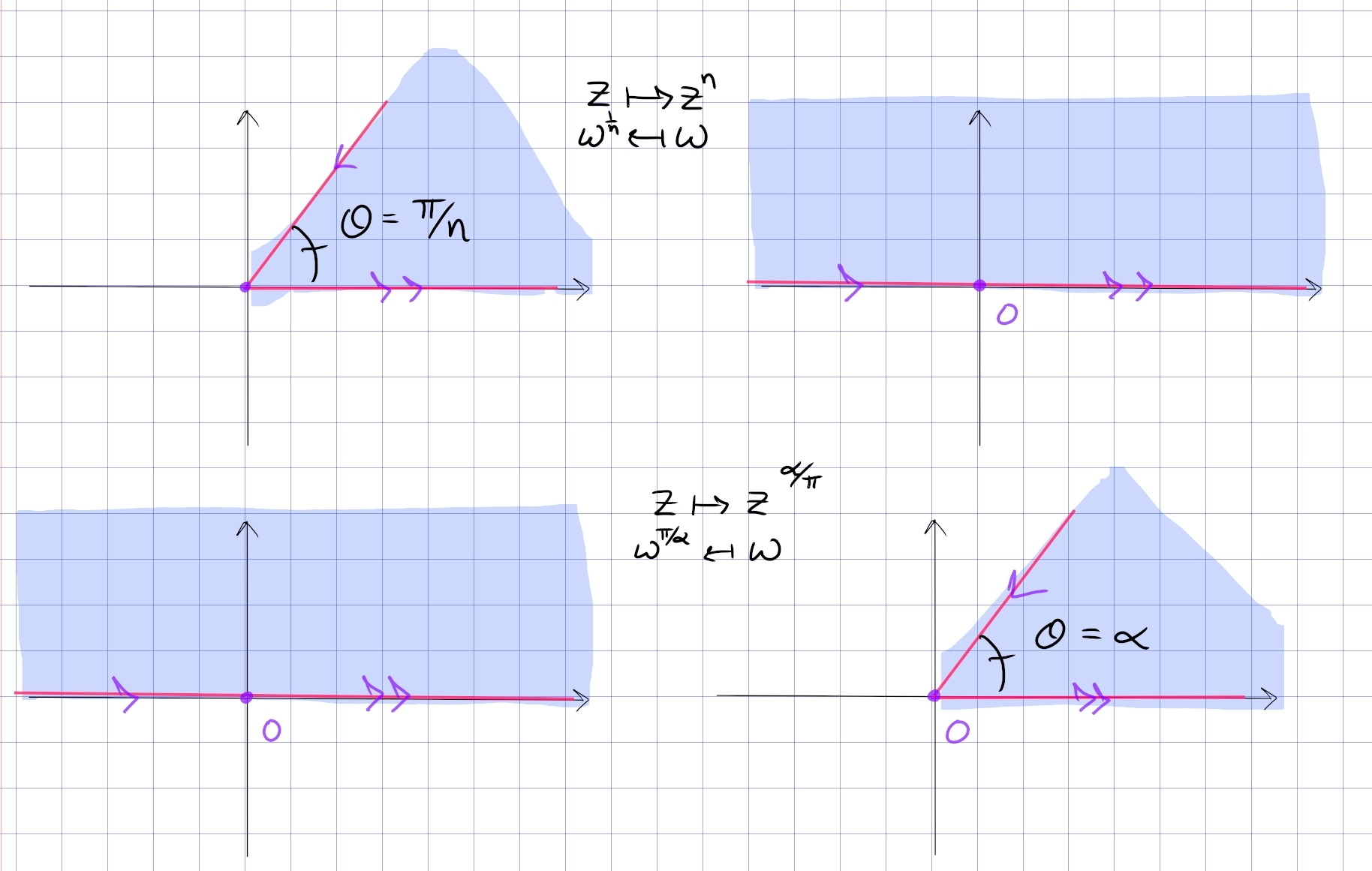
\begin{align*}\left\{{\operatorname{Arg}(z) \in (-\theta_0, \theta_0) }\right\} \xrightarrow{z^a} \left\{{\operatorname{Arg}(z) \in (-a\theta_0, a\theta_0) }\right\}\end{align*}
Generally,
\begin{align*}\left\{{\operatorname{Arg}(z) \in (-\theta_0, \theta_0) }\right\} \xrightarrow{z^a} \left\{{\operatorname{Arg}(z) \in (-a\theta_0, a\theta_0) }\right\}\end{align*}
-
Unfolding a symmetric sector:
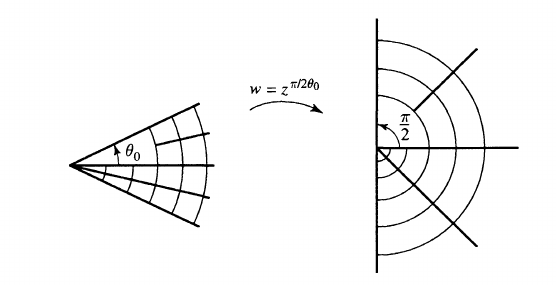
\begin{align*}z\mapsto z^{\pi \over 2\theta_0}: \left\{{\operatorname{Arg}(z) \in (-\theta_0, \theta_0)}\right\}\to \left\{{\operatorname{Arg}(z) \in (-\pi/2, \pi/ 2)}\right\}.\end{align*}
-
-
Some variants:
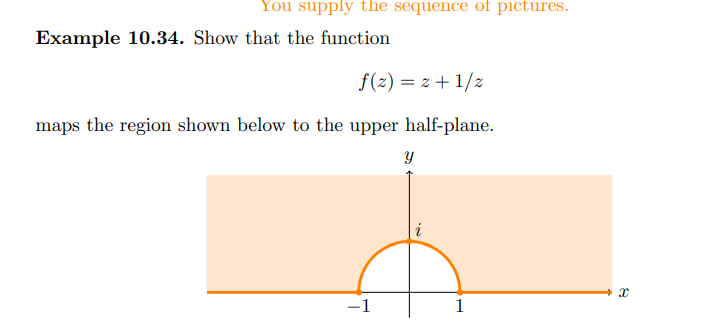
- Half-discs to planes: the Joukowski maps \(z\mapsto z+z^{-1}\)
-
Bigons/lunar domains: map the intersection points \(z_0\to 0, z_1\to\infty\) to get strips.
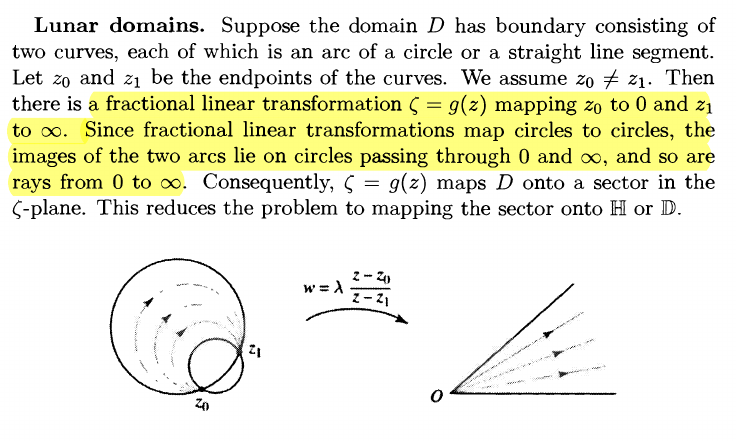
- In general, take the line through the centers and intersection points. Call the intersection of the two circles \(a\), the line with the small circle \(b\), and the last \(c\), and take \((z; c,b,a)\) to get \(0<\Re(z) < 1\).
Some tips:
- A computational shortcut: \(z^{-1}= {\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu\over {\left\lvert {z} \right\rvert}^2}\). Use this to quickly compute images, e.g. for \({\left\lvert {z-1} \right\rvert} = 1\) under \(f(z) = 1/z\), write \(f(1+i)={1\over 1+i} = {1-i \over 2}\).
- The locus of points equidistant to two fixed points is the perpendicular bisector.
-
Seems obvious, but use that conformal maps preserve angles. You can use tangent vectors to reason about angles of intersection (even at \(z=\infty\)). E.g. Since \({\left\lvert {z-i} \right\rvert}=1\) intersects \({\mathbb{R}}\) in a parallel way, since the tangent vectors at zero will line up. So any conformal map must send them to parallel lines or circles with intersection angle zero.
- Similarly if two circles intersect orthogonally, they must go to orthogonal lines or a line orthogonally intersecting a circle.
- \(z\mapsto 1/z\) corresponds to a rotation of \({\mathbb{CP}}^1\) around the \(x{\hbox{-}}\)axis by \(\pi\).
The Big 9 Conformal Maps
\({\mathbb{H}}\) and \({\mathbb{D}}\)
\begin{align*} \Psi: {\mathbb{H}}&\rightleftharpoons{\mathbb{D}}\\ z &\mapsto {z-i \over z+i} \\ i \qty{1+w \over 1-w} &\mapsfrom w .\end{align*}
Mnemonic: every \(z\in {\mathbb{H}}\) is closer to \(i\) than \(-i\). This restricts to a map \begin{align*} \Psi: Q_1 &\rightleftharpoons{\mathbb{D}}\cap{\mathbb{H}} .\end{align*}
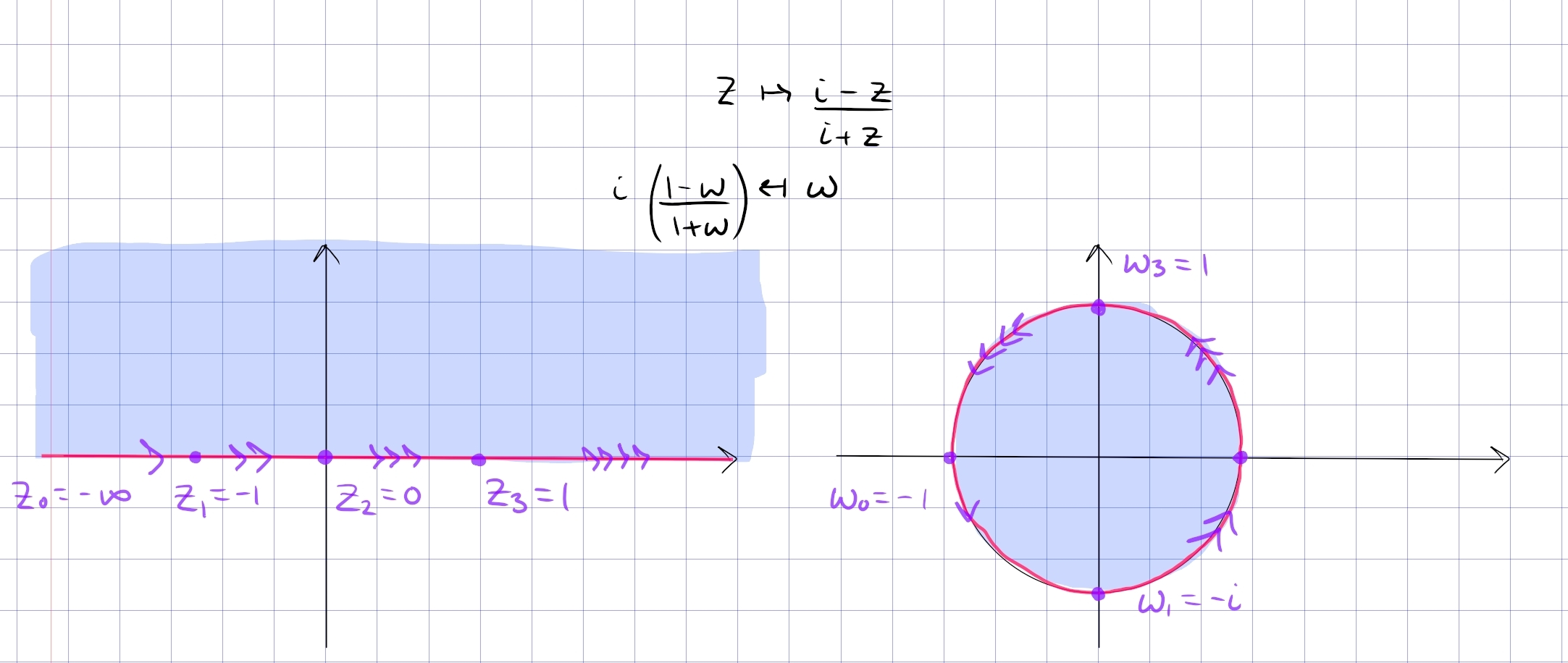

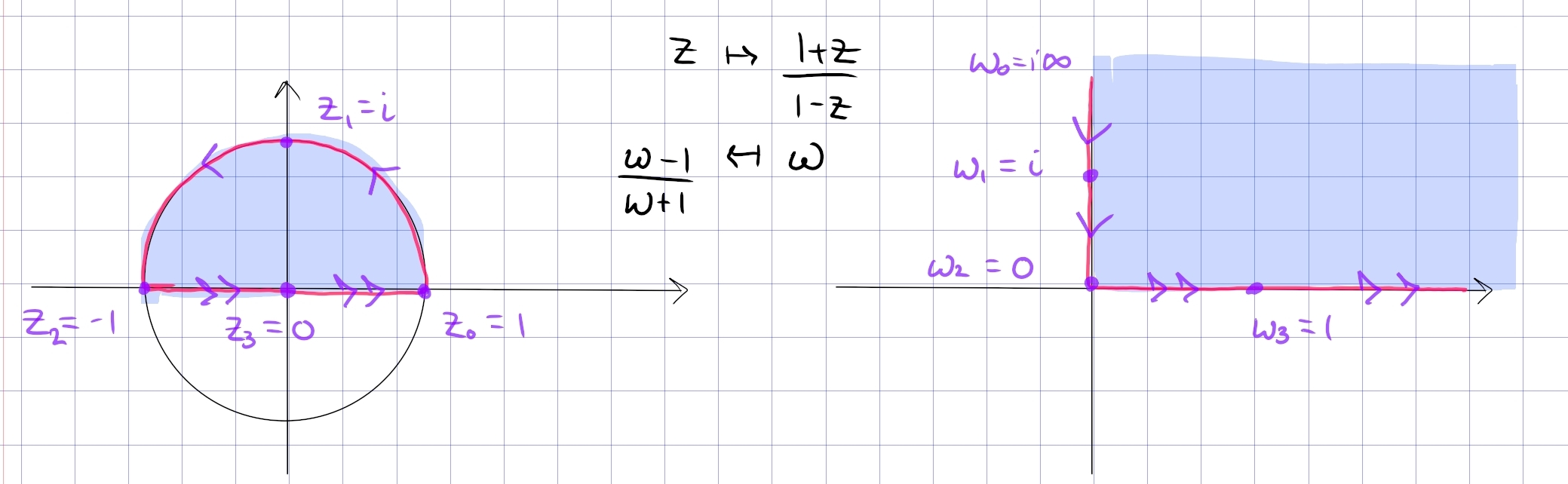
\begin{align*} F: {\mathbb{D}}&\mapsto Q_{12} \coloneqq\left\{{\Re(z) > 0}\right\} \\ z &\mapsto {1+z \over 1-z} \\ {w-1\over w+1} &\mapsfrom w .\end{align*}
This satisfies \begin{align*} {\left[ {-1, 0, 1} \right]} \mapsto {\left[ {0, 1, \infty} \right]} .\end{align*}
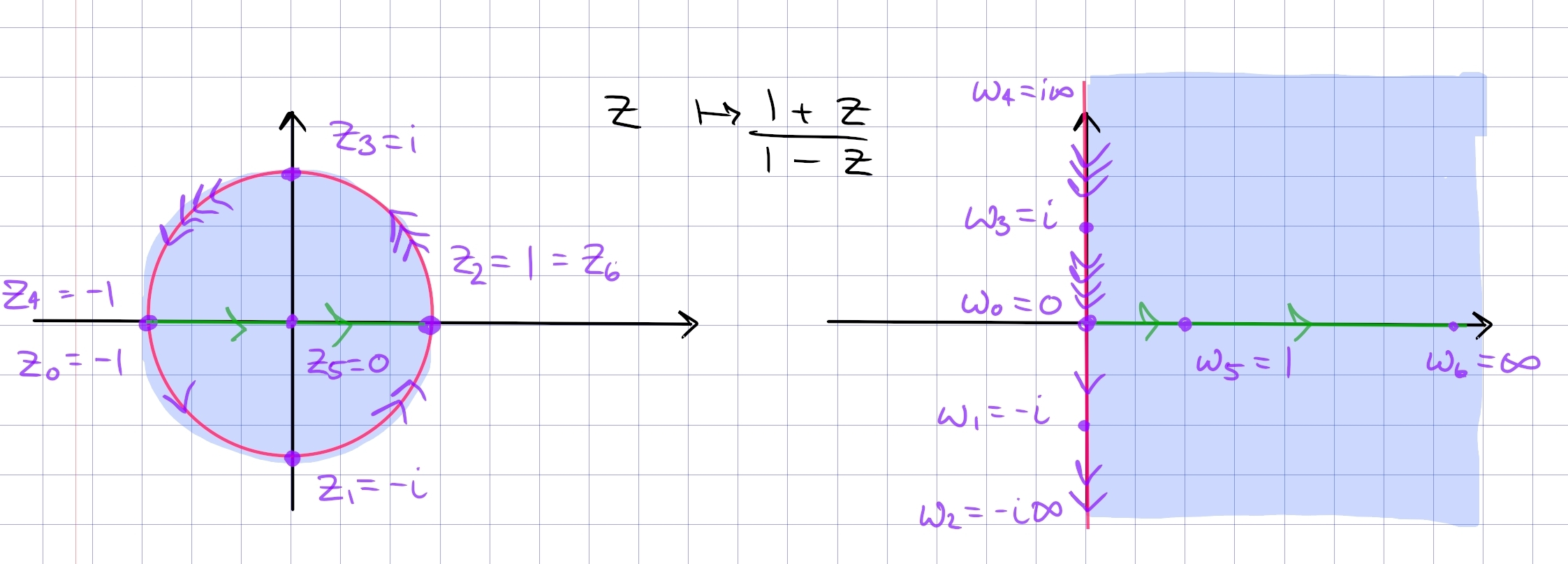
Note that \(\Psi\) inverse from above can be recovered by post-composing with a rotation by \(\pi/2\): \begin{align*} \Psi^{-1}(z) = i\qty{1+z\over1-z} = i \cdot F(z) && {\mathbb{D}}\xrightarrow{F} Q_{12} \xrightarrow{\cdot i} {\mathbb{H}} ,\end{align*} and up to a negative sign, we can recover \(\Psi\) by recomposition with a rotation by \(-\pi/2\): \begin{align*} F(-iz) = {1+ iz \over 1-iz} = {-i + z \over -i-z} = -{z-i\over z+i} = -\Psi(z) && {\mathbb{H}}\xrightarrow{\cdot -i} Q_{12} \xrightarrow{F} {\mathbb{D}} .\end{align*}
This restricts to a map \(F: {\mathbb{D}}\cap{\mathbb{H}}\to Q_1\):
-
Why this lands in the first quadrant:
- Use that squares are non-negative and \(z=x+iy\in {\mathbb{D}}\implies x^2 + y^2 < 1\): \begin{align*} f(z)=\frac{1-\left(x^{2}+y^{2}\right)}{(1-x)^{2}+y^{2}}+i \frac{2 y}{(1-x)^{2}+y^{2}} .\end{align*}
-
Why the inverse lands in the unit disc:
- For \(w\) in Q1, the distance from \(w\) to 1 is smaller than from \(w\) to \(-1\).
- Check that if \(w=u+iv\) where \(u, v>0\), the imaginary part of the image is positive:
` \begin{align*} {w-1 \over w+1} &= { (w-1) \mkern 1.5mu\overline{\mkern-1.5mu(w+1)\mkern-1.5mu}\mkern 1.5mu \over {\left\lvert {w+1} \right\rvert}^2}\ &={ \qty{u-1 + iv} \qty{u+1-iv} \over (u+1)^2 + v^2 } \ &= {u^2 + v^2 + 1 \over (u+1)^2 + v^2}
- i\qty{ 2v \over (u+1)^2 + v^2} .\end{align*} `{=html}
Boundary behavior:
- On the upper half circle \(\left\{{ e^{it } {~\mathrel{\Big\vert}~}t\in (0, \pi) }\right\}\), write \begin{align*} f(z)=\frac{1+e^{i \theta}}{1-e^{i \theta}}=\frac{e^{-i \theta / 2}+e^{i \theta / 2}}{e^{-i \theta / 2}-e^{i \theta / 2}}=\frac{i}{\tan (\theta / 2)} ,\end{align*} so as \(t\) ranges \(0\to \pi\) we have \(f(z)\) ranging from \(0\to i\infty\) along the imaginary axis.
Sectors
\begin{align*} F: \left\{{z{~\mathrel{\Big\vert}~}\operatorname{Arg}(z) \in \qty{0, {\pi \over n}} }\right\} &\to {\mathbb{H}}\\ z &\mapsto z^n \\ w^{1\over n} &\mapsfrom w .\end{align*}
More generally, for \(0 < \alpha < 2\), \begin{align*} F: {\mathbb{H}}&\to \left\{{z{~\mathrel{\Big\vert}~}\operatorname{Arg}(z) \in \qty{0, \alpha} }\right\} \\ z &\mapsto z^{\alpha\over \pi} \\ w^{\pi \over \alpha} &\mapsfrom w .\end{align*}
Logs and Exponentials
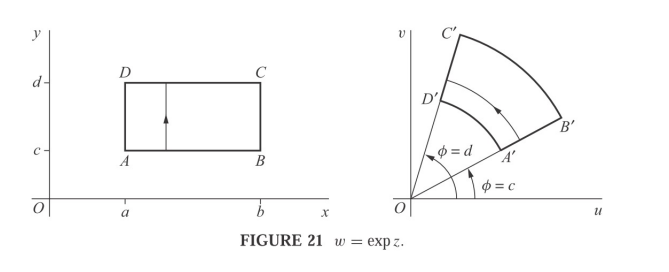
The exponential generally sends boxes to sectors, so \begin{align*} \left\{{z {~\mathrel{\Big\vert}~}\Re(z) \in [a, b], \Im(z)\in [c, d]}\right\}\mapsto \left\{{Re^{i\theta} {~\mathrel{\Big\vert}~}R \in [e^a, e^b], \theta\in [c, d]}\right\} .\end{align*}
Pictures of the situation:
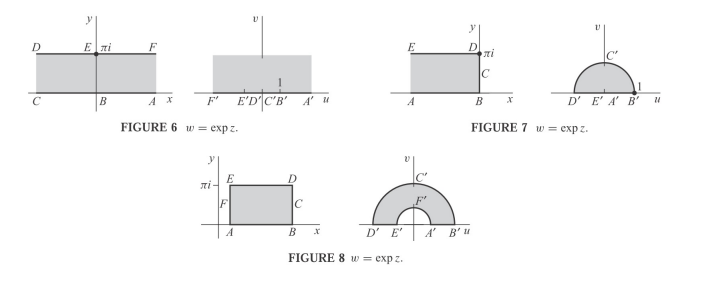
\begin{align*} F: {\mathbb{H}}&\to {\mathbb{R}}\times i(0, \pi) \\ z &\mapsto \operatorname{Log}(z) \\ e^w &\mapsfrom w .\end{align*}
- Why this lands in a strip: use that \(\arg(z) \in (0, \pi)\) and \(\log(z) = {\left\lvert {z} \right\rvert} + i\arg(z)\).
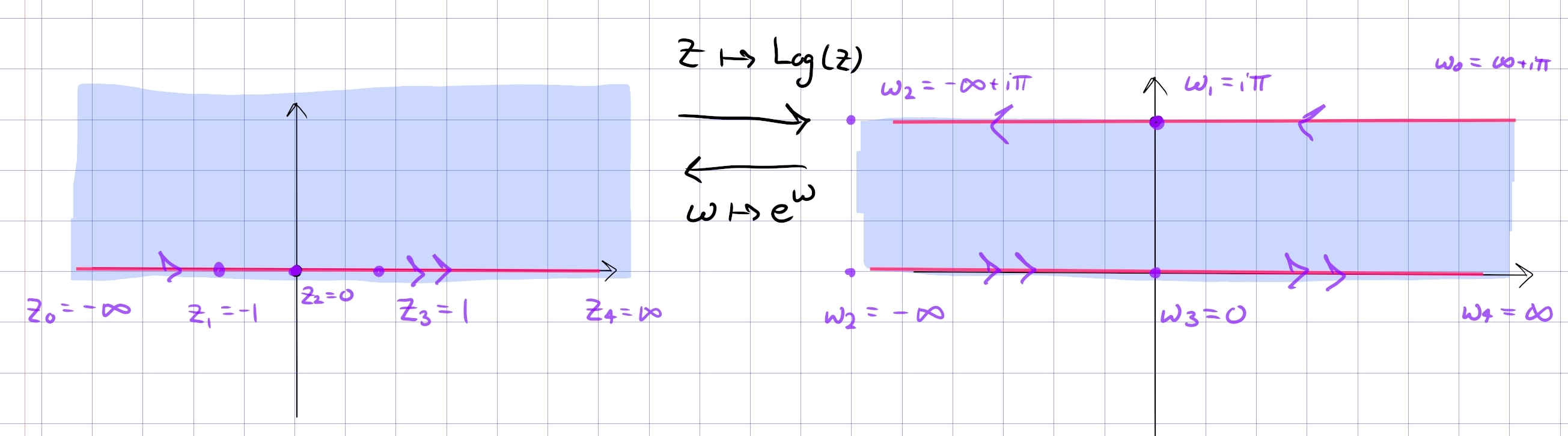
\begin{align*} F: {\mathbb{C}}\setminus{\mathbb{R}}_{\leq 0} &\to {\mathbb{R}}\times i(-\pi, \pi) \\ z &\mapsto \operatorname{Log}(z) .\end{align*}
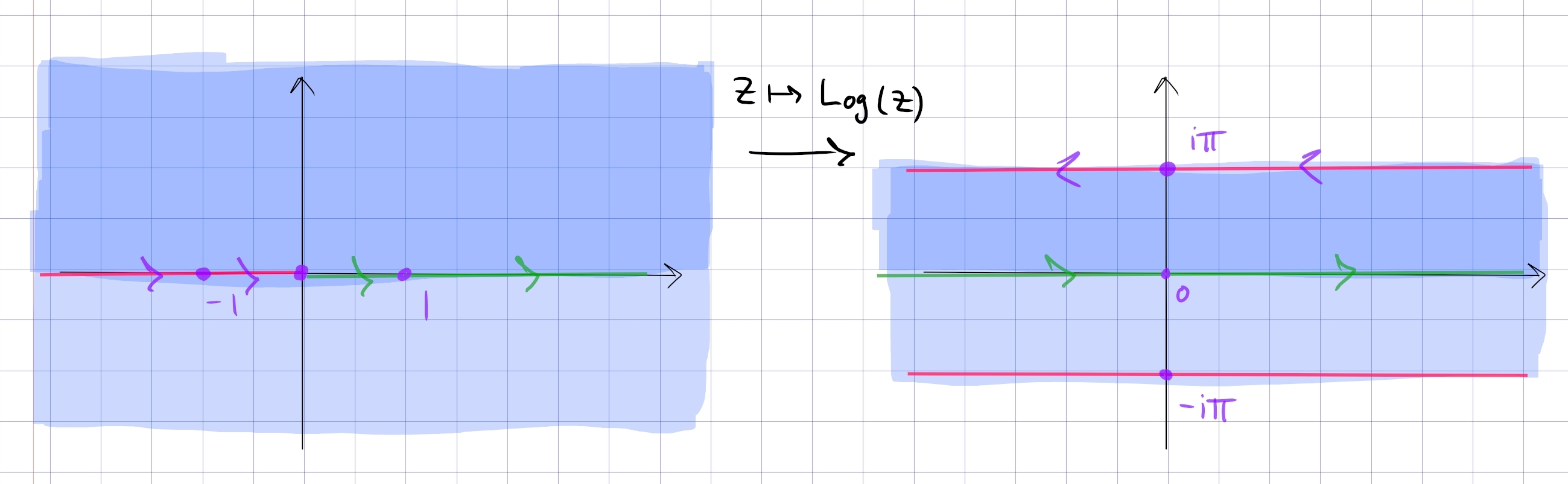
- Circles of radius \(R\) are mapped to vertical line segments connecting \(\ln(R) + i\pi\) to \(\ln(R) - i\pi\), and rays are mapped to horizontal lines.
- Inverse is useful: \(z\mapsto e^z\) sends \(\left\{{ {\left\lvert { \Re(z) } \right\rvert} < \pi/2 }\right\}\) to \(Q_{14}\), the right half-plane.
\begin{align*} F: {\mathbb{D}}\cap{\mathbb{H}}&\to {\mathbb{R}}_{<0} \times i (0, i\pi) \\ z &\mapsto \operatorname{Log}(z) \\ e^w &\mapsfrom w .\end{align*}
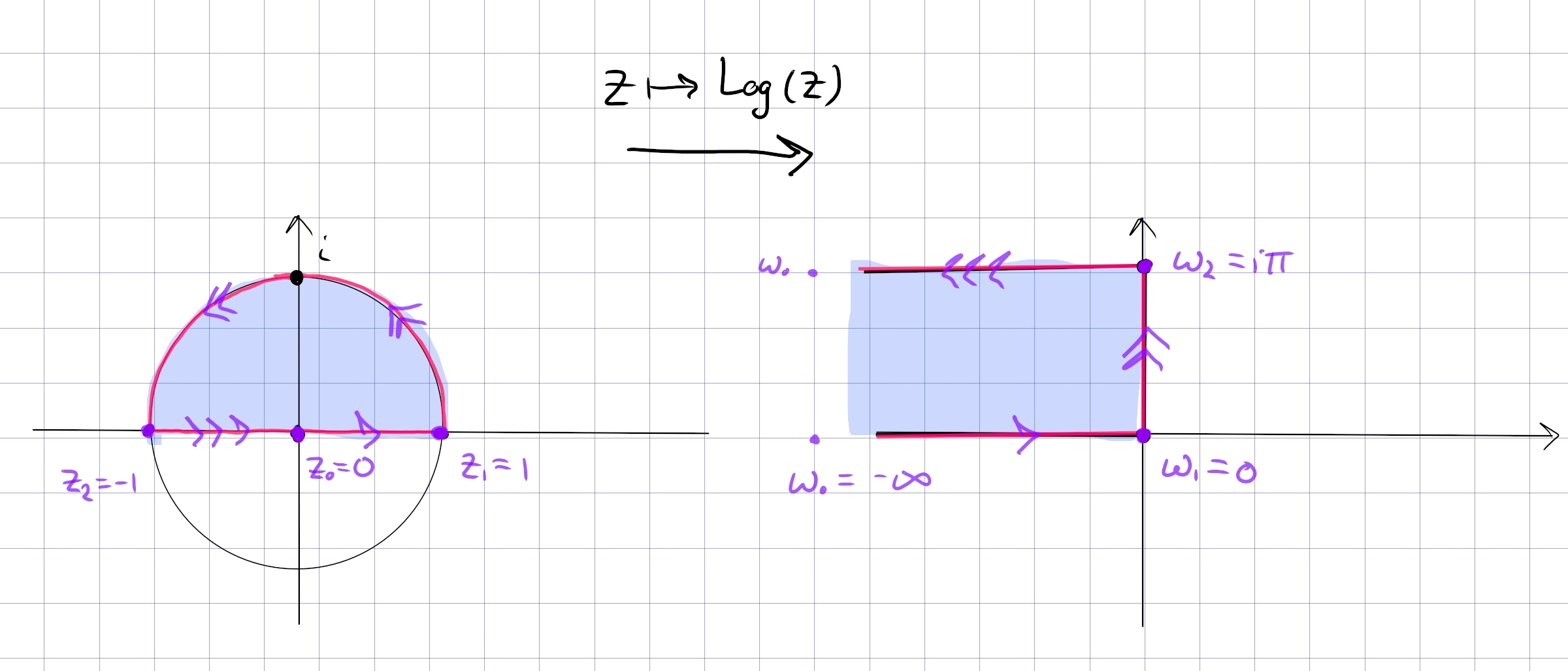
In general,
- \({\mathbb{D}}\cap{\mathbb{H}}\) maps to a half-strip in \(Q_2\)
- \({\mathbb{D}}\cap Q_{34}\) maps to a half-strip in \(Q_1\).
- \({\mathbb{D}}^c \cap{\mathbb{H}}\) maps to a half-strip in \(Q_1\)
- \({\mathbb{D}}^c \cap Q_{34}\) maps to a half-strip in \(Q_4\)
\begin{align*} F: \qty{-{\pi \over 2}, {\pi \over 2}} \times i{\mathbb{R}}&\to {\mathbb{D}}\cap\left\{{\Re(z) > 0}\right\} \\ z &\mapsto e^{iz} \\ -i\operatorname{Log}(w) &\mapsfrom w .\end{align*}
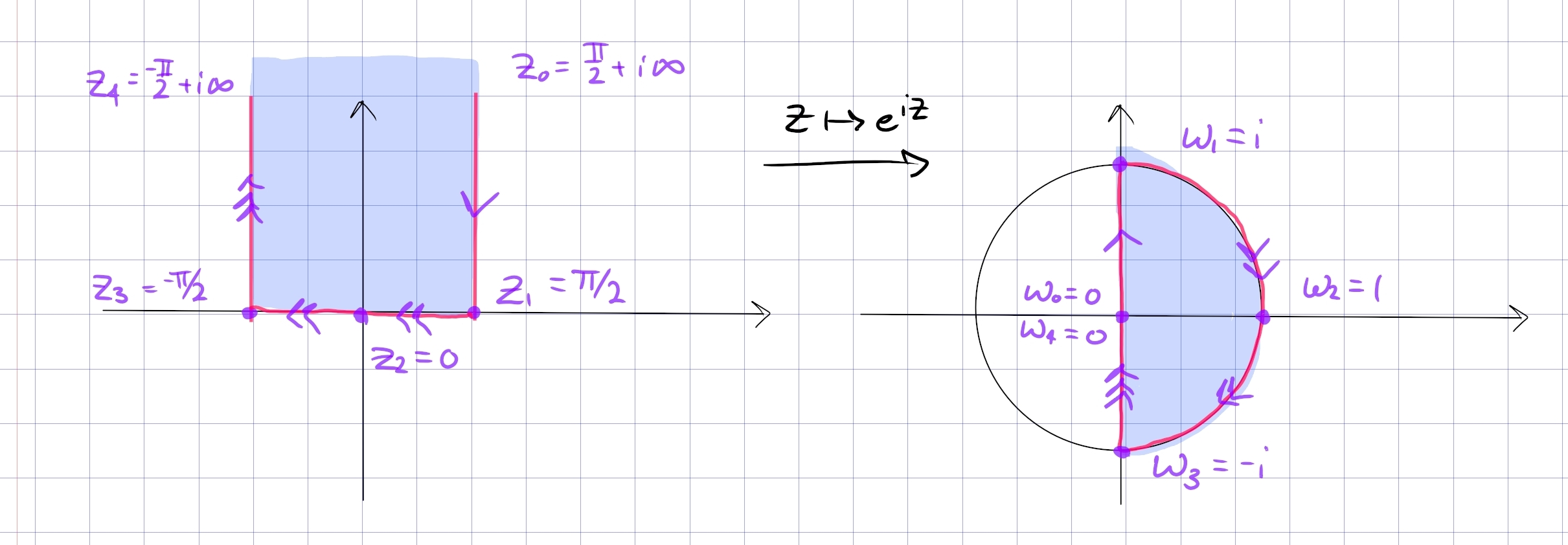
This is essentially polar coordinates: write \(e^z = e^{-y} e^{ix}\), then \(x\in (-\pi/2, \pi/2)\) and \(y\in (0, \infty)\) so this fills out a half-disc as \(x,y\) vary.
Joukowski Maps
A nice resource: https://complex-analysis.com/content/joukowsky_airfoil.html

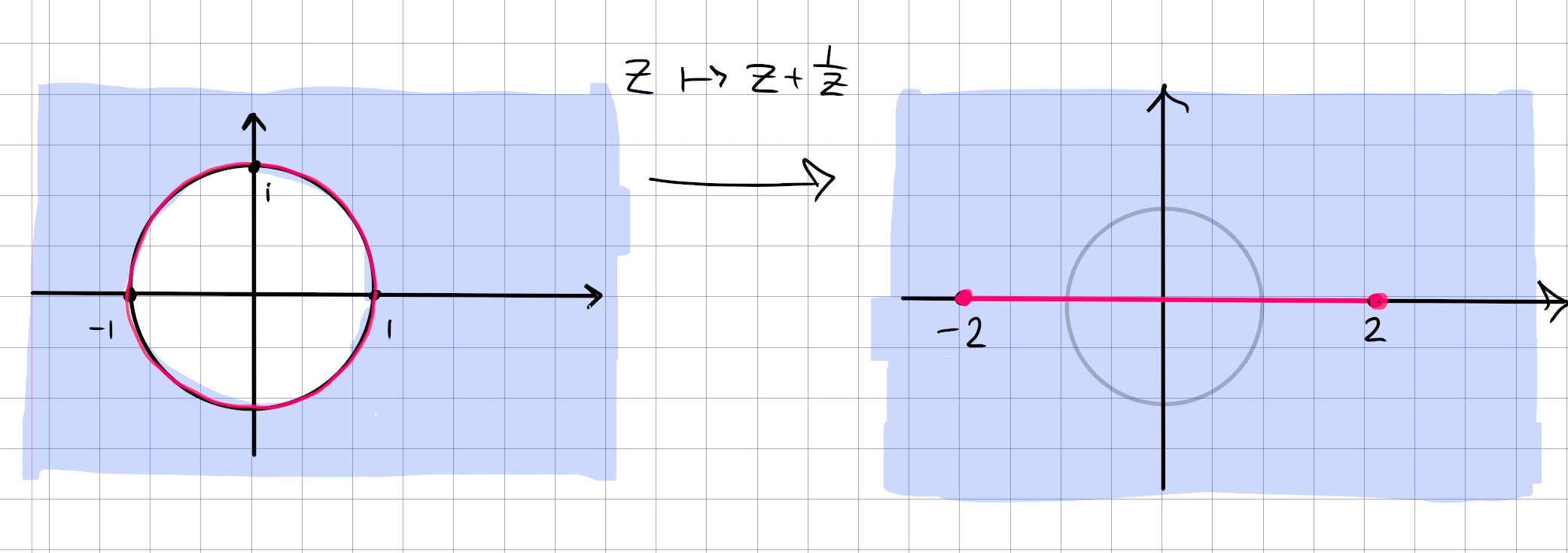
In general, \(z\mapsto z+z^{-1}\) has the following effects:
- \({\left\lvert {z} \right\rvert} = 1\) is mapped onto \([-2, 2]\)
- \({\mathbb{D}}\cap{\mathbb{H}}\) is mapped to \(Q_{34}\)
- \({\mathbb{D}}^c \cap{\mathbb{H}}\) is mapped to \({\mathbb{H}}\)
- \({\mathbb{D}}^c\) is mapped to \({\mathbb{C}}\setminus[-2, 2]\)
\begin{align*} F: {\mathbb{D}}^c \cap{\mathbb{H}}&\to {\mathbb{C}}\setminus[-2, 2] \\ z &\mapsto z+ z^{-1} .\end{align*}
\begin{align*} F: {\mathbb{D}}\cap{\mathbb{H}}&\to {\mathbb{H}}\\ z & \mapsto -{1\over 2}\qty{ z + z^{-1}} .\end{align*}
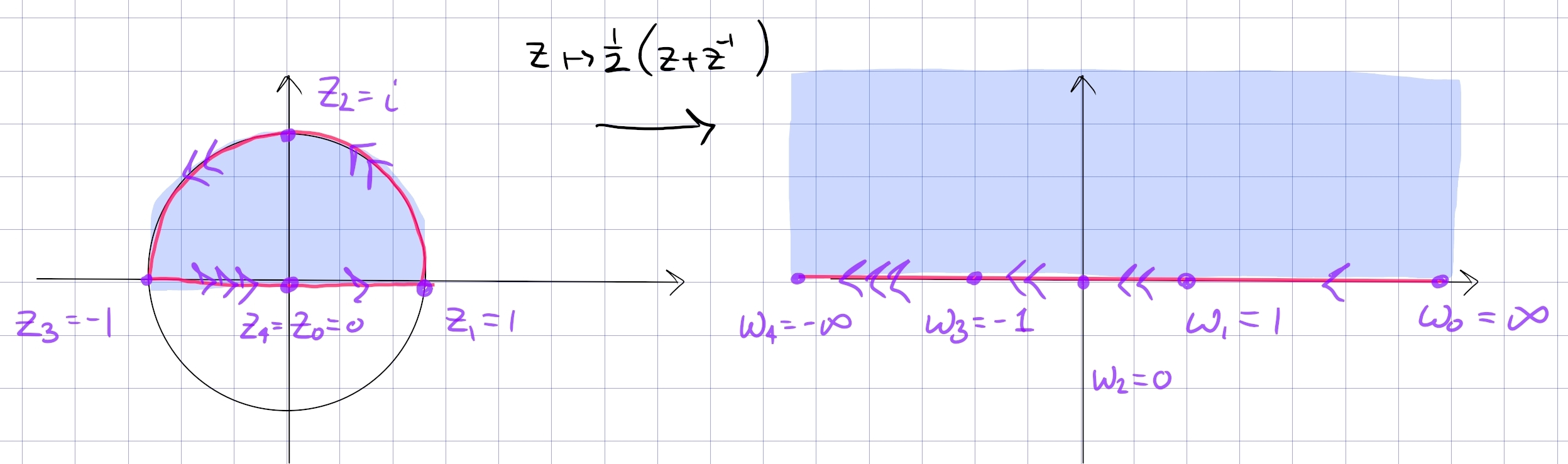
- It additionally maps \({\mathbb{D}}^c\to {\mathbb{R}}\setminus[-1, 1]\).
- A similar variant: \(z\mapsto {1\over 2i}(z+z^{-1})\) sends \(Q_{14}\) to \({\mathbb{C}}\setminus\left\{{t\in {\mathbb{R}}{~\mathrel{\Big\vert}~}{\left\lvert {t} \right\rvert} \geq 1}\right\}\), the plane with a slit on \({\mathbb{R}}\) through infinity (i.e. a doubly slit plane).
This is sometimes referred to as a Joukowski map.o The inverse is a bit complicated.
\begin{align*} F: {\mathbb{H}}&\to \qty{-{\pi \over 2}, {\pi \over 2}} \times i{\mathbb{R}}\\ z &\mapsto \sin(z) .\end{align*}
The mapping \(z\mapsto \sin(z)\): 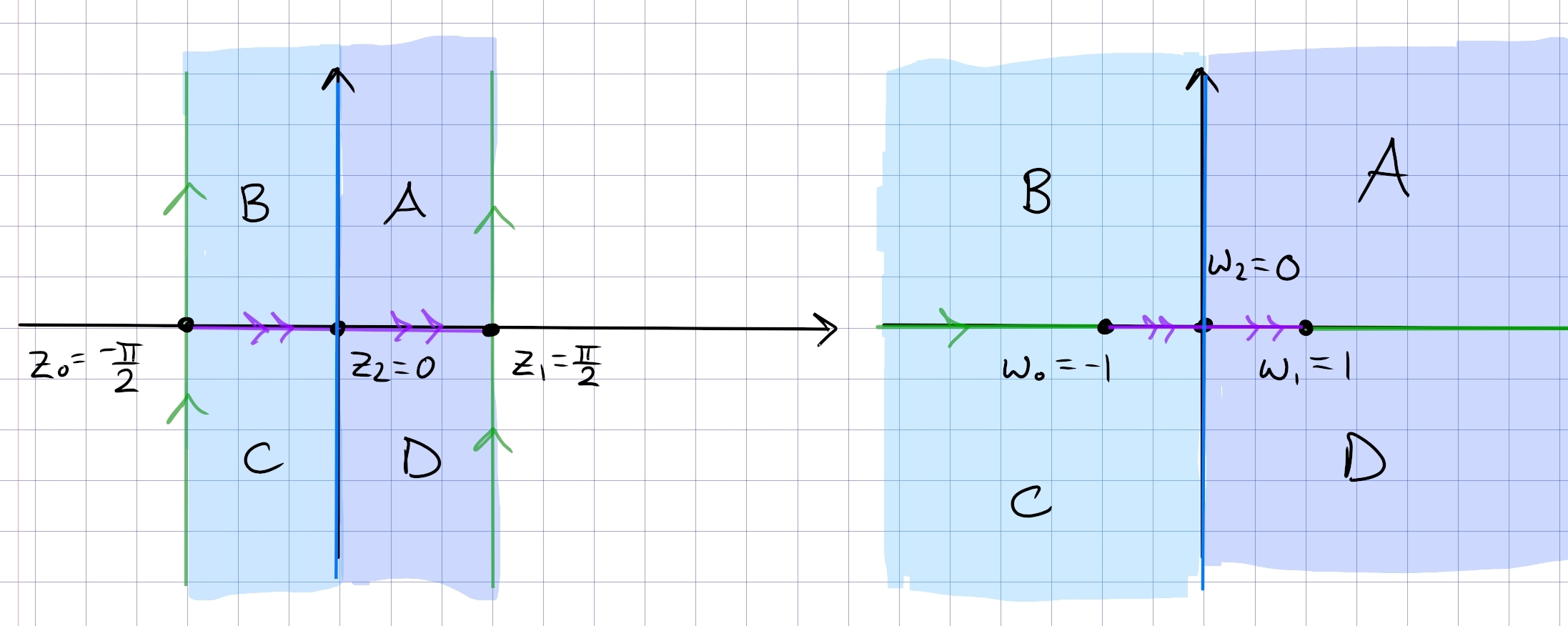
- As \(z\) travels from \(i\infty \to i0\), \(\sin(iz) = i\sinh(z)\) also traverses \(i\infty\to i0\)
- For \(z\in[-\pi/2, \pi/2]\), \(\sin(z)\) is real and in \([-1, 1]\).
- As \(z\) travels along \(\pi/2 + it\) for \(t\in [0, \infty)\), \(\sin(\pi/2 + it) = \cosh(t)\) traverses \(1\to \infty\) along \({\mathbb{R}}\)
Note that this isn’t new: set \(w \coloneqq e^{iz}\), then \begin{align*} \sin(z) = -{1\over 2}\qty{iw + {1\over iw}} ,\end{align*} which is the composition \begin{align*} \qty{z \mapsto e^{z} } \circ \qty{z\mapsto iz} \circ \qty{z\mapsto {1\over 2}(z+z^{-1})} .\end{align*}