Exercises: Conformal Maps

Use cross ratios: set \(T(z) \coloneqq(z;,1,i,2)\) and \(S(w) = (w;,3,0,-1)\) and solve \(T(z) = S(w) \implies w = (S^{-1}T)(z)\): \begin{align*} {z-i \over z-2}{1-2\over 1-i} &= {w-0\over w+1}{3+1 \over 3-0} \\ \implies -\frac{\left(i + 1\right) \, {\left(z - i\right)}}{2 \, {\left(z - 2\right)}} &= \frac{4 \, w}{3 \, {\left(w + 1\right)}} \\ \implies w &= -\frac{3 \, {\left(\left(i + 1\right) \, z - i + 1\right)}}{\left(3 i + 11\right) \, z - 3 i - 13} \\ &= - {3z - 3i \over {3i+11\over i+1}z + {-3i-13 \over 3i+11}} \\ &= - {3z - 3i \over (7-4i) z + {-8+5i} } \\ &= \frac{-3 z+3 i}{(7-4 i) z+(-8+5 i)} .\end{align*}

Idea: all cross-ratios send the complement of a positively oriented region \((a,b,c)\) to the half-hemisphere \((1,0,\infty)\) on \({\mathbb{CP}}^1\). So take \((i, -1, 1)\to (1,0,\infty)\):

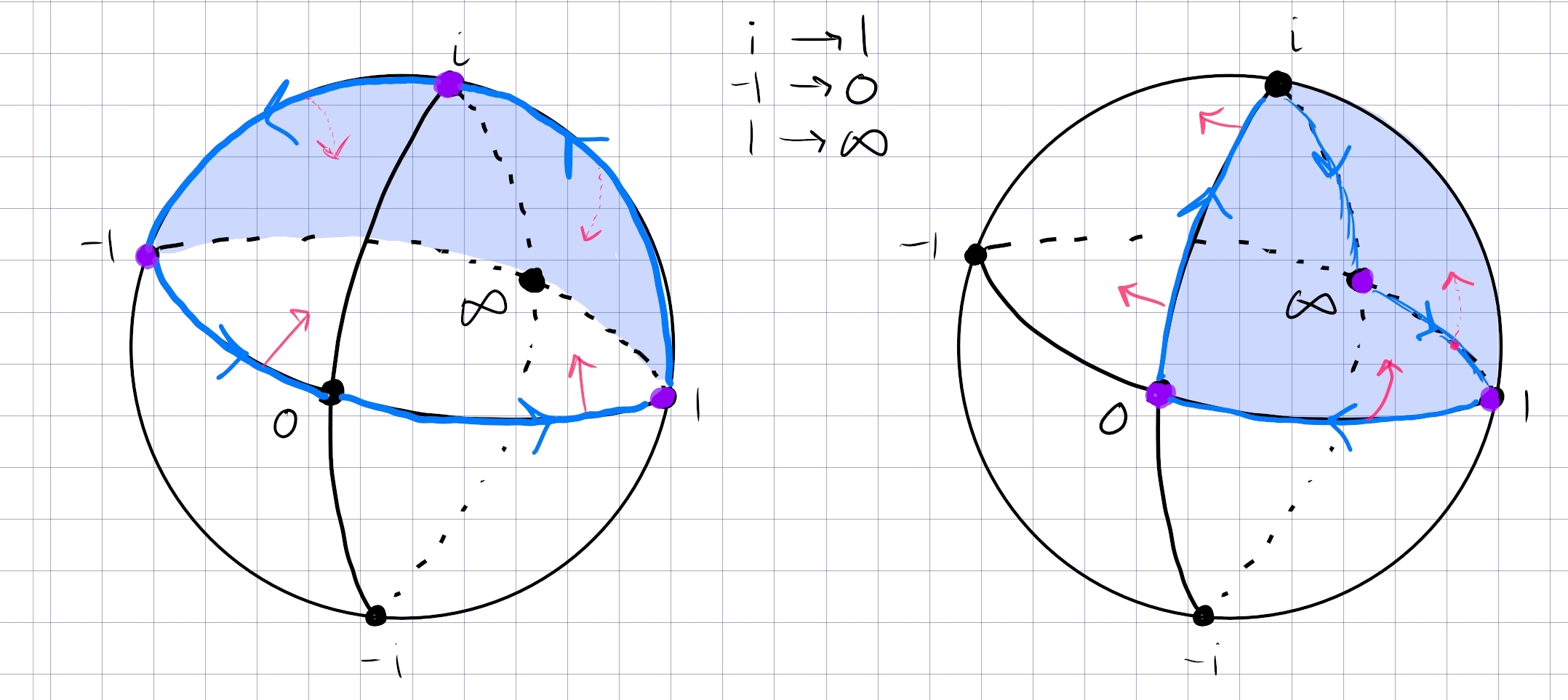
This is the cross-ratio \begin{align*} f(z) = {z+1\over z-1} {i-1\over i+1} .\end{align*}

The image of \({\mathbb{D}}^c \cap{\mathbb{H}}\) is the 1st quadrant \({\mathbb{H}}\cap\Re(z) > 0\). Send this to \({\mathbb{H}}\) with \(z\mapsto z^2\).

Unclear to me how to motivate this formula, but choose \(f(z) = {z-i\over z+i}\). Note that

• \(f(-1) = i\)
• \(f(0) = -1\)
• \(f(1) = -i\),

so \({\mathbb{R}}\) oriented from \(-\infty\to\infty\) is sent to \(S^1\) oriented counterclockwise. Since this is conformal, it preserves handedness – noting that \({\mathbb{H}}\) is on the left with respect to \({\mathbb{R}}\), it gets mapped to the left of \(S^1\) with its induced orientation, i.e. the interior of \({\mathbb{D}}\). How to remember: \({\left\lvert {z-i} \right\rvert}<{\left\lvert {z+i} \right\rvert}\) in \({\mathbb{H}}\), since points are closer to \(i\) than \(-i\).

The image of the first quadrant: the claim is that this is \({\mathbb{D}}\cap Q_{34}\). Note that parameterizing seems hard! The naive idea would be to check the image of horizontal lines \(t + ci\) for \(c\) fixed heights and \(t\in (0, \infty)\) the parameterization. Instead consider handedness and where sub-regions go:

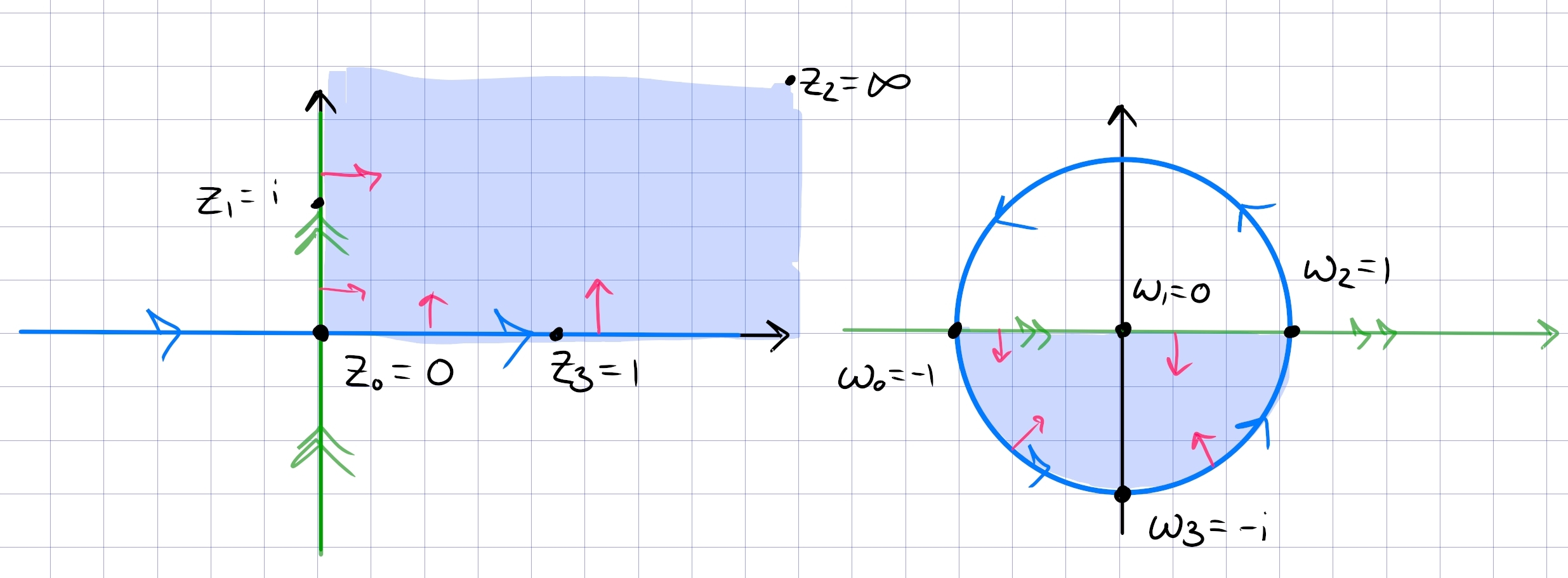
Noting that \(Q_1\) is the bigon enclosed by \(0, \infty\), this maps to a bigon spanned by \(-1, 1\). By handedness, since \(Q_1\) is to the left of \({\mathbb{R}}\), it gets mapped to the left of the image of \({\mathbb{R}}_{>0}\), which is the lower half of the circle.

Idea: rotate the upper hemisphere \(({\mathbb{H}})\) of \({\mathbb{CP}}^1\) to make the equator \({{\partial}}{\mathbb{D}}\), “zoom” by placing \(i\) at the center so \(0\to i\mapsto -1\to 0\) and \(i\to \infty\mapsto 0\to 1\). Accomplish this by sending

• \(\infty\to 1\)
• \(i\to 0\)
• \(-i\to \infty\)

Use the cross-ratio \begin{align*} R(z) \coloneqq(z, \infty, i, -i) = {z-i \over z-(-i)} {\infty - (-i) \over \infty - i} = {z-i\over z+i} .\end{align*}

Checking that this works:

• If \(z\in {\mathbb{R}}\) then \({\left\lvert {z-i} \right\rvert} = {\left\lvert {z+i} \right\rvert}\) so \({\left\lvert {F(z)} \right\rvert} = 1\).
• If \(z\in {\mathbb{H}}\) then \({\left\lvert {z-i} \right\rvert}\leq {\left\lvert {z+i} \right\rvert}\) so \({\left\lvert {F(z)} \right\rvert}< 1\).

Note that the standard Cayley map \(f(z)\coloneqq{z-i\over z+i}\) sends \({\mathbb{H}}\to {\mathbb{D}}\). Why this is true: \({\left\lvert {f(z)} \right\rvert} < 1\), since \({\left\lvert {z-i} \right\rvert} < {\left\lvert {z+i} \right\rvert}\) for \(z\in {\mathbb{H}}\). Finding an explicit inverse: \begin{align*} w &= {z-i\over z+i} \\ \implies w(z+i) - (z-i) &= 0 \\ \implies z &= -i {w+1\over w-1} ,\end{align*} which is the desired map. Why the image is in \({\mathbb{H}}\): it suffices to show that \(\Im(f(z)) > 0\) for all \(z\in {\mathbb{D}}\). Write \(z = x+iy\) and note that \(\Im(iz) = \Re(z)\), then \begin{align*} \Im(f(z)) &= \Re\qty{1-z\over 1+z} \\ &= \Re\qty{1-x-iy \over 1+x+iy} \\ &= \Re\qty{1-x^2-y^2 - i2y \over 1+x^2 + y^2} \\ &= {1-(x^2+y^2) \over 1+(x^2+y^2) } \\ &> 0 ,\end{align*} since \(x^2+y^2<1\) for \(x+iy \in {\mathbb{D}}\).

Note that \(z\mapsto z^2\) doesn’t actually work, because the image is \({\mathbb{D}}\setminus{\mathbb{R}}_{\geq 0}\) and has a slit deleted. Instead compose:

• \(z\mapsto i{z-1\over z+1}\), which maps \({\mathbb{D}}\to {\mathbb{H}}\) and restricts to map \({\mathbb{D}}\cap{\mathbb{H}}\to Q_1\).
• \(z\mapsto z^2\), which maps \(Q_1\to {\mathbb{H}}\)
• \(z\mapsto {z-i\over z+i}\) which maps \({\mathbb{H}}\to {\mathbb{D}}\).

In parts:

• Use \(z\mapsto z^{-1}\) to send \({\mathbb{H}}\cap{\mathbb{D}}\) to \(Q_{34} \cap{\mathbb{D}}^c\).
• Use \(z\mapsto -z\) to map this to \({\mathbb{H}}\cap{\mathbb{D}}^c\)
• Use \(z\mapsto {1\over 2}(z+z^{-1})\) to map \({\mathbb{H}}\cap{\mathbb{D}}^c\) to \({\mathbb{H}}\)
• Then use the Cayley map \(z\mapsto {z-i\over z+i}\) to map \({\mathbb{H}}\to {\mathbb{D}}\).

• \(z\mapsto {1+z\over 1-z}\) is a standard map \({\mathbb{D}}\to Q_{14}\) which restricts to \({\mathbb{D}}\cap{\mathbb{H}}\to Q_1\)
• \(z\mapsto z^2\) unwraps \(Q_1\to {\mathbb{H}}\).

Claim: the map \(f(z) \coloneqq z+z^{-1}\) works. Consider the images of circles \(\gamma_r(t) \coloneqq rei^{t}\) where \(t\in [-\pi, \pi]\). For \(r=1\), \begin{align*} f(\gamma_1(t)) = e^{it} + e^{-it} = 2\cos(t) ,\end{align*} which sweeps out \([-2, 2]\) twice. For arbitrary \(r\), \begin{align*} f(\gamma_r(t)) = re^{it} + r^{-1}e^{-it} = (r+r^{-1})\cos(t) +i(r-r^{-1})\sin(t) ,\end{align*} which sweeps out an ellipse with horizontal radius \(r+r^{-1}\) and vertical radius \(r-r^{-1}\). For \(1<r<\infty\), these sweep out all of \({\mathbb{C}}\setminus{\mathbb{D}}\). Restricting \(t\in [0, \pi]\), the \(\gamma_r(t)\) are top halves of circles which cover all of \({\mathbb{H}}\setminus{\mathbb{D}}\), and the images \(f(\gamma_r(t))\) are top halves of ellipses which sweep out all of \({\mathbb{H}}\). This includes points inside of \({\mathbb{D}}\cap{\mathbb{H}}\) – this is because for any \(t\in (0, \infty)\), there is always a solution \(r\) to \(t=r-r^{-1}\): \begin{align*} t = r-r^{-1}\implies r^2-tr-1 \implies r = {t \pm \sqrt{t^2+4}\over 2} .\end{align*} So there is an image ellipse at that vertical height. Since every point \(z_0\in {\mathbb{H}}\) is on an ellipse of some vertical height \(t\), \({\mathbb{H}}\) is in the image.

That this map is conformal: a computation shows \(f'(z) = 1 + {1\over r^2}\), which vanishes only at \(z=\pm 1\). Since these are not in the domain, the derivative is nonvanishing, making \(f\) conformal.

The picture:

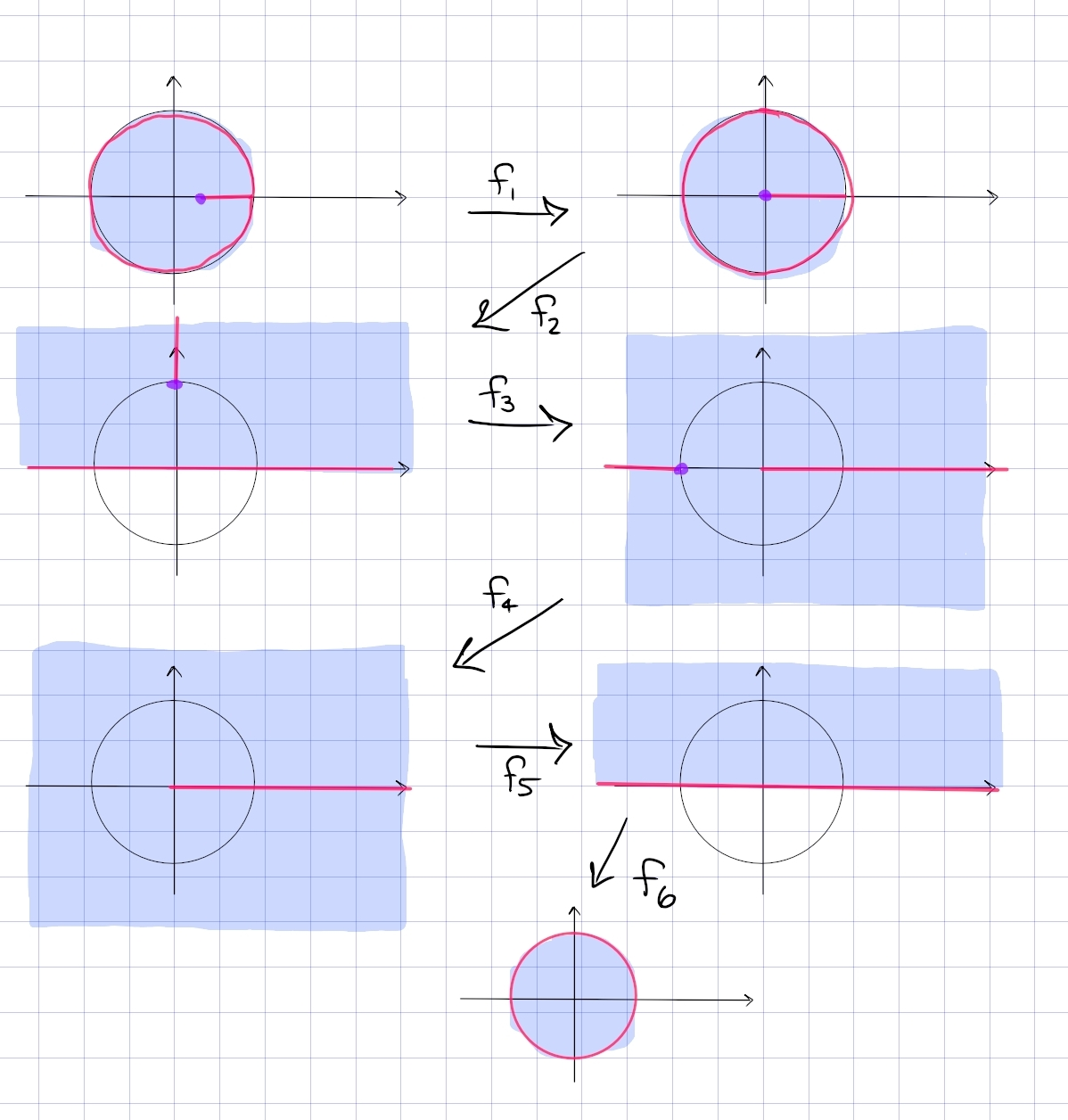
In steps:

• \(f_1\): send \(1/2\to 0\) and \(1\to 1\) in order to lengthen the slit. Mobius transformations preserve lines, so take \(f_1(z) = {z-1/2 \over 1-1/2}\). New domain: \({\mathbb{D}}\setminus[0, 1)\).

• \(f_2\): send \({\mathbb{D}}\to {\mathbb{H}}\) and keep track of the slit. Use the standard inverse to the Cayley transform, \(f_2(z) = i{1-z\over 1+z}\). New domain: \({\mathbb{H}}\setminus[i, i\infty)\), noting that \({\mathbb{H}}\) is the open half-plane.

• \(f_3\): rotate the slit so it becomes a line segment from \(-1\) to \(1\) passing through \(\infty\). Use \(f_3(z) = z^2\). New domain: \({\mathbb{C}}\setminus\qty{(-\infty, 1] \cup[1, \infty) }\)

• \(f_4\): move the slit off to infinity to be left with a ray, so send \(-1\to \infty\) and \(0\to 0\). Take \(f_4(z) = {z\over z+1}\), the new domain is \({\mathbb{C}}\setminus[0, \infty)\).

• \(f_5\): fold it back. Branch cut log along \([0, \infty)\) to define \(f_5(z) = z^{1\over 2}\), so the new domain is \({\mathbb{H}}\).

• \(f_6\): apply the standard Cayley transform \(f_6(z) = {i-z\over i+z}\)

In steps:

• Dilate by \(z\mapsto \pi z\) to get \(0<\Im(z) < \pi\).
• Exponentiate by \(z\mapsto e^z\) to get \({\mathbb{H}}\).

Why \(e^z\) works: apply \(\operatorname{Log}\) to \({\mathbb{H}}\), use polar coordinates to write \(w=re^{i\theta}\) with \(0<\theta<\pi\) and note \begin{align*} \operatorname{Log}(w) = \ln{\left\lvert {w} \right\rvert} +i\operatorname{Arg}(w) = \ln(r) + i\theta ,\end{align*} and noting that the image of \(\ln({-})\) is all of \({\mathbb{R}}\).

The key insight: for lunes, map the corners to \(0\) and \(\infty\); this yields a sector. Here we want \(-1\mapsto 0\) and \(1\mapsto \infty\), so \(f(z) = {z+1\over z-1}\) gets things started.

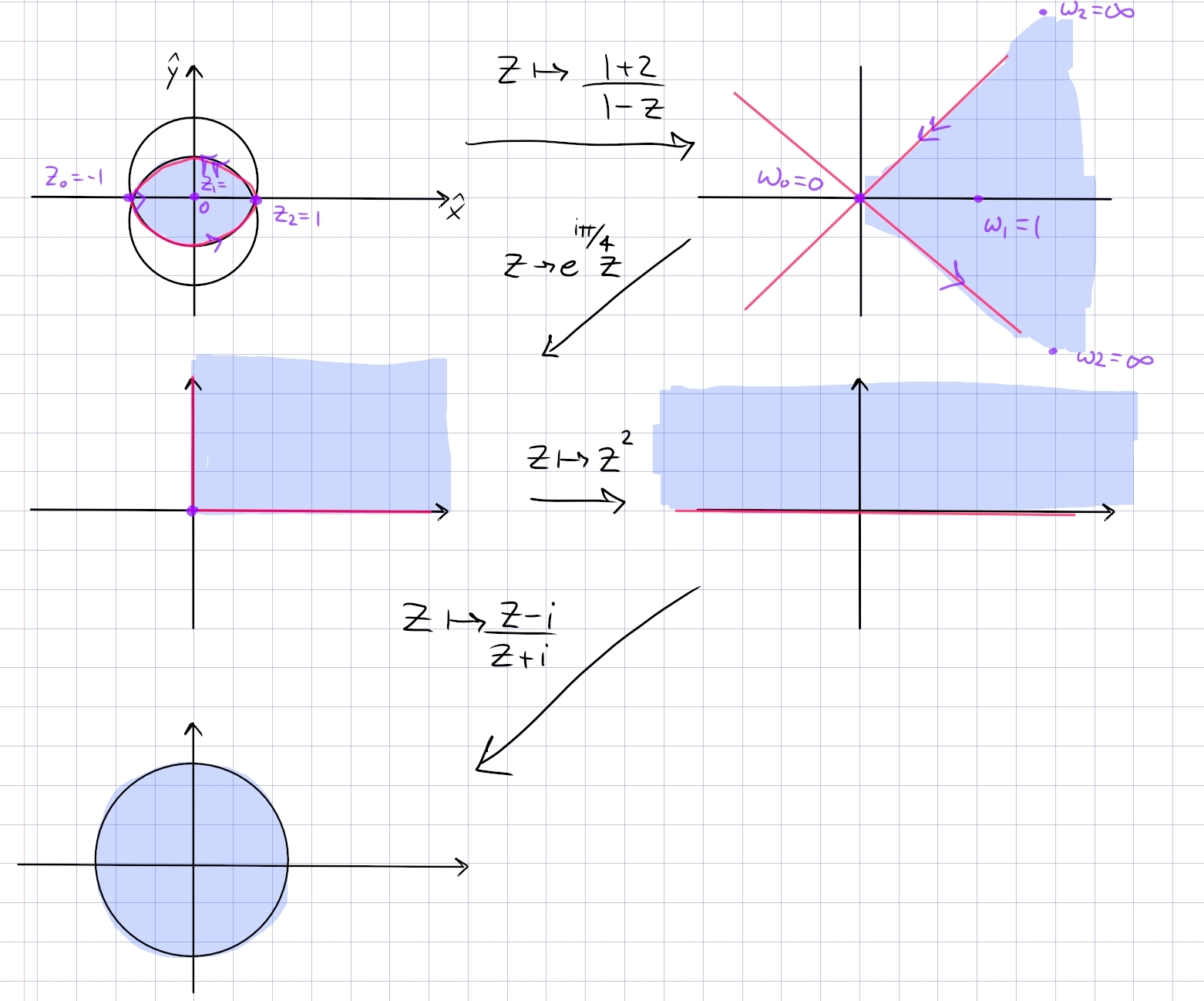
In steps:

• \(z\mapsto {1+z\over 1-z}\) sends the lune to the sector \(\operatorname{Arg}(z) \in (-\pi/4, \pi/4)\), since it fixes and must be symmetric about the real axis, and preserves the right angle between the circles at \(z=-1\).
• \(z\mapsto e^{i\pi/4}z\) to rotate this into \(Q_1\).
• \(z\mapsto z^2\) to dilate into \({\mathbb{H}}\).
• \(z\mapsto {z-i\over z+i}\) the standard Cayley map \({\mathbb{H}}\to{\mathbb{D}}\).

The picture:

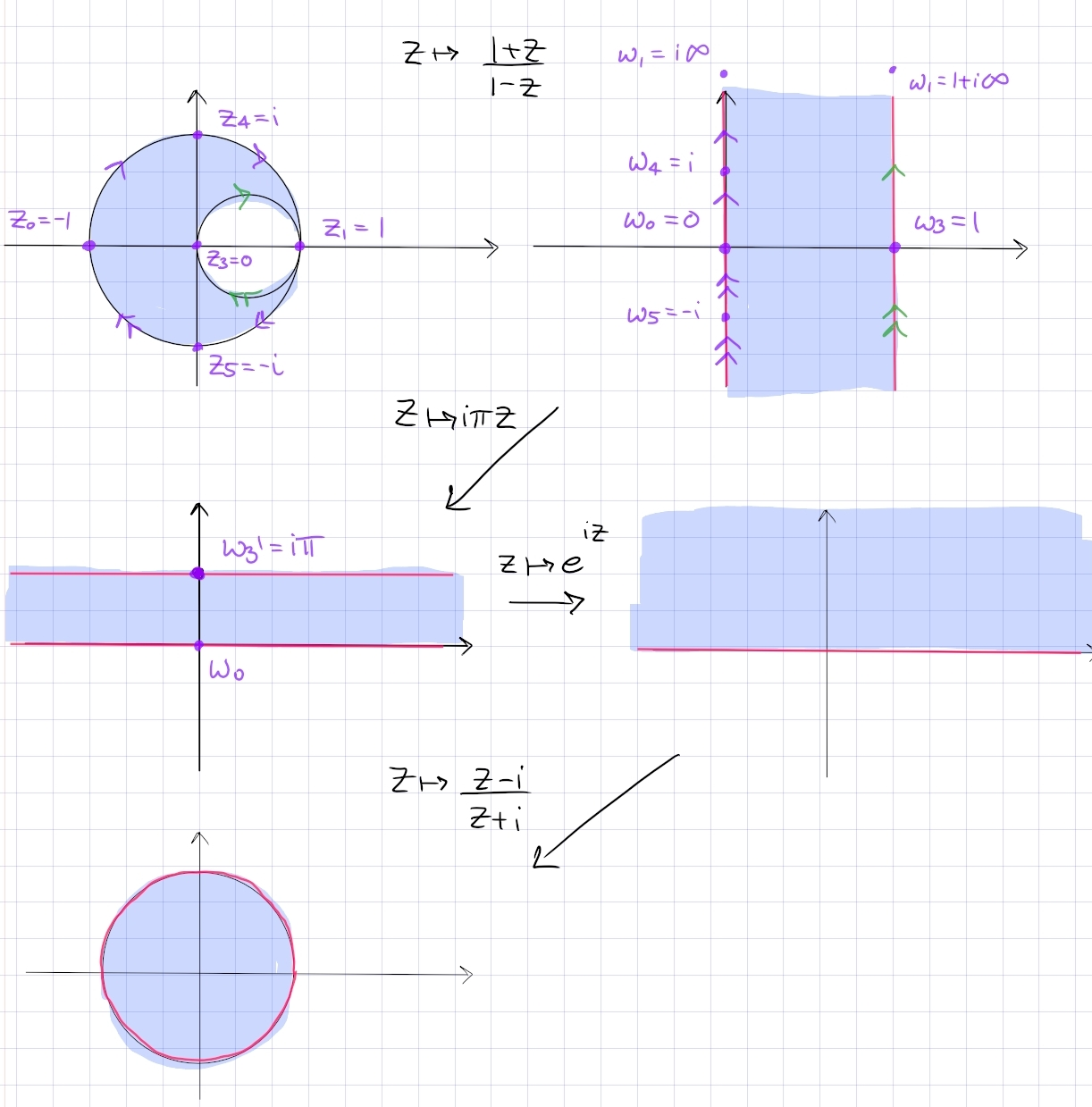
• Key insight: send the point of tangency to \(\infty\) to get parallel lines. Send \(z\mapsto {1+z \over 1-z}\) to send \(-1\to 0, 0\to 1, 1\to \infty\) to get a vertical strip.

• Rotate and dilate: \(z\mapsto i\pi z\) to get a strip \({\mathbb{R}}\times i(0, \pi)\).

• Standard exponential \(z\mapsto e^{iz}\) sends this to \({\mathbb{H}}\).

• Standard Cayley \(z\mapsto {z-i \over z+i}\) sends this to \({\mathbb{D}}\).

The picture:

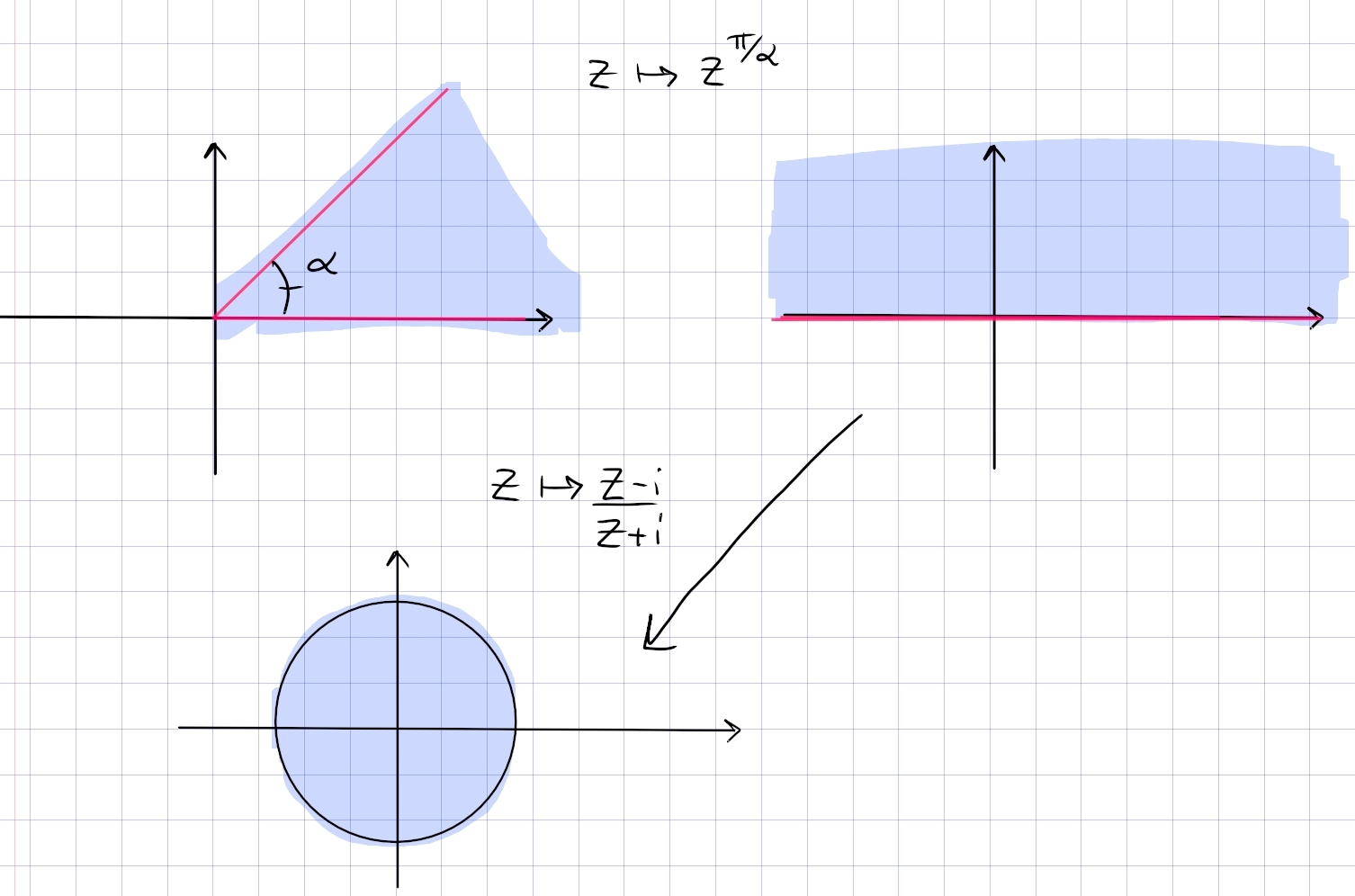
In steps:

• Map the sector to \({\mathbb{H}}\) using \(z\mapsto z^{\pi/\alpha}\), choosing a branch cut for \(\operatorname{Log}\) along \({\mathbb{R}}_{\leq 0}\).
• Map \({\mathbb{H}}\to {\mathbb{D}}\) using the standard \(z\mapsto {z-i\over z+i}\).

In steps:

• Send \(-1\to 0\) and \(1\to \infty\) with \(z\mapsto {z+1\over z-1}\). Checking that \(f(0) = -1\), this yields \({\mathbb{C}}\setminus{\mathbb{R}}_{\leq 0}\).

• Unwrap with \(z\mapsto \sqrt{z}\) to obtain the right half-plane \(-\pi/2<\operatorname{Arg}(z) < \pi/2\).

• Apply the rotated Cayley map \(z\mapsto {z-1\over z+1}\) to map this to \({\mathbb{D}}\).

Note that the composition is \begin{align*} {\sqrt{z+1\over z-1} -1 \over \sqrt{z+1\over z-1} +1} &= { \qty{ \sqrt{z+1} - \sqrt{z-1}}^2 \over (z+1)-(z-1) } \\ &= z - \sqrt{z^2-1} ,\end{align*} which has inverse \(z\mapsto {1\over 2}\qty{z+{1\over z}}\).

Idea: need the line \(-i\infty\to 0 \to i\infty\) to get mapped to a circle \(0\to 1\to 0\):

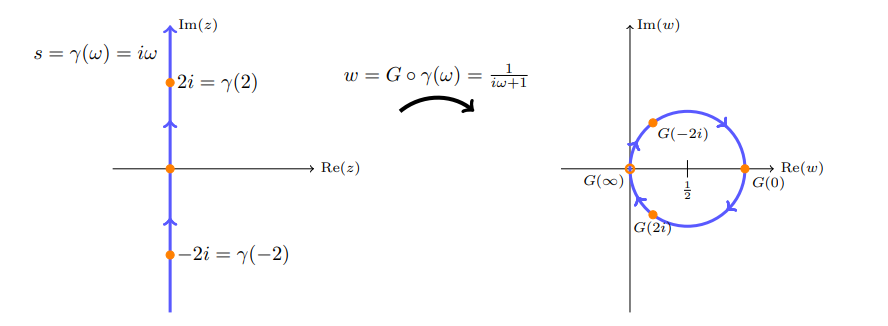
Take the cross ratio \(R(z) = (z, 0, \infty, -1)\) to send

• \(0\to 1\)
• \(\infty\to 0\)
• \(-1\to \infty\)

This yields \begin{align*} R(z) = {z-\infty \over z+1}{0+1\over 0-\infty} = {1\over z+1} .\end{align*} Some deductions:

• \(R\) preserves circles, so \({\mathbb{R}}\mapsto {\mathbb{R}}\).
  • The segment \(0\to\infty\mapsto 1\to 0\)
  • The ray \(-1\to 0 \to \infty \mapsto \infty\to 1\to 0\)
  • The ray \(-\infty \to -1 \mapsto 0\to -\infty\)
• \(R\) preserves angles, to at \(w=0\), the image of \(i{\mathbb{R}}\) must be orthogonal to \({\mathbb{R}}\), so it’s either a circle or \(i{\mathbb{R}}\) itself.
• Check \(-i\infty \to 0 \to -\infty\mapsto 0\to 1\to 0\), so the image is a circle.
• Parameterize \(i{\mathbb{R}}= \left\{{it{~\mathrel{\Big\vert}~}t\in {\mathbb{R}}}\right\}\), then compute the image \begin{align*} f(i{\mathbb{R}}) &= \left\{{{1\over 1+it}}\right\} \\ &= \left\{{1+t\over 1+t^2}\right\} \\ &= \left\{{{1\over 1+t^2} + i {t\over 1+t^2}}\right\} \\ &= \left\{{{1\over 2} \qty{ 1 + {1-t^2\over 1+t^2} } + i{1\over 2}\qty{2t\over 1+t^2}}\right\} \\ &= \left\{{{1\over 2}\qty{1 + \cos(2t) + i\sin(2t)}}\right\} \\ &= \left\{{{1\over 2} + {1\over 2}e^{2it} }\right\} ,\end{align*} which is a circle of radius \(1/2\) about \(1/2\).

Conclusion:

• \(i{\mathbb{R}}\to \left\{{{\left\lvert {z-{1\over 2}} \right\rvert} = {1\over 2} }\right\}\) by \(z\to {1\over 1+z}\).
• The reverse map: \(w\mapsto {1-w\over w}\).

Compose to get: \begin{align*} {1\over z}{z + z^{-1}} .\end{align*}