If \(\Omega \subseteq {\mathbb{C}}\) with \(\pi_1 \Omega = 1\) then \(\Omega\) is biholomorphic to \({\mathbb{D}}\).
If \(\Omega\) is simply connected, nonempty, and not all of \({\mathbb{C}}\), then for every \(z_{0}\in \Omega\) there exists a unique conformal map \(F:\Omega \to {\mathbb{D}}\). Moreover, it can be arranged so that \(F(z_{0}) = 0\) and \(F'(z_{0}) > 0\).
Thus any two such sets \(\Omega_{1}, \Omega_{2}\) are conformally equivalent.
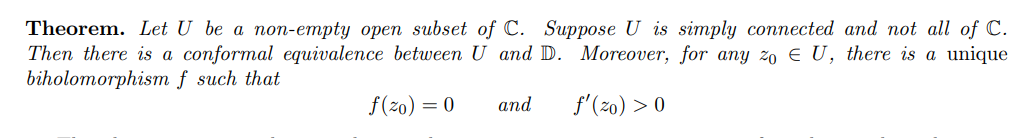
Necessity of hypothesis:
- Not all of \({\mathbb{C}}\): \(F: {\mathbb{C}}\to \Omega\) with \(\Omega\) bounded implies \(F\) is constant by Liouville.
- Simply connected: since \(\pi_1 {\mathbb{D}}= 1\), any closed curve in \(\Omega\) is nullhomotopic by finding \(F\) and composing \(F^{-1}\) with a homotopy in \({\mathbb{D}}\).
The basic idea:
- Consider the set \({\mathcal{F}}\) of conformal \(h: \Omega\to {\mathbb{D}}\) with \(h(z_0) = 0\) and \(h'(z_0) > 0\) which are not necessarily surjective.
- Show there is a maximal \(f\in {\mathcal{F}}\), and show \(f\) is surjective.
More details:
-
Fix some \(z_0\in \Omega\) and set \({\mathcal{F}}= \left\{{f\in \mathop{\mathrm{Hol}}(\Omega, {\mathbb{D}}) {~\mathrel{\Big\vert}~}f(z_0) = 0, f \text{ injective }}\right\}\). A lemma will show \({\mathcal{F}}\) is nonempty.
-
Define the hyperbolic translations and compute \begin{align*} h_w(z) &\coloneqq{z-w \over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \in \mathop{\mathrm{Hol}}({\mathbb{D}}) h'_w(0) &= 1 - {\operatorname{ab}}{w}^2 \\ h'_w(w) &= {1\over 1 - {\left\lvert {w} \right\rvert}^2} .\end{align*}
-
Show that if \(f\in {\mathcal{F}}\) is not surjective, one can find another member with a larger derivative of \(z_0\), say \(g\) with \({\left\lvert {g'(z_0)} \right\rvert} > {\left\lvert {f'(z_0)} \right\rvert}\).
-
Show that \({\mathcal{F}}\) is uniformly bounded and thus normal by Montel.
-
Define \(m\coloneqq\sup_{f\in {\mathcal{F}}} {\left\lvert {f'(z_0)} \right\rvert}\), noting that \(0<m<\infty\) since the maps are conformal and the Cauchy estimate supplies an upper bound: \begin{align*} {\left\lvert {f'(z_0)} \right\rvert} \leq \max_{{\left\lvert {z-z_0} \right\rvert} = R} { {\left\lvert {f(z)} \right\rvert} \over R} \leq {1\over R} .\end{align*}
-
Produce a sequence \(\tilde {\mathcal{F}}= \left\{{f_k}\right\}\) such that \({\left\lvert {f_k'(z_0)} \right\rvert} \overset{k\to\infty}\longrightarrow m\).
-
Apply Montel to \(\tilde {\mathcal{F}}\) which are uniformly bounded by 1 to extract a subsequence that converges locally uniformly to some \(h\).
-
Show \(h\in {\mathcal{F}}\) by showing \(h(z_0) = 0\), is analytic, and non-constant. Apply Hurwitz’s theorem to conclude \(h\) is injective as a uniform limit of injective functions.
-
Show \(h\) is surjective by showing \({\left\lvert {h'(z_0)} \right\rvert} \geq {\left\lvert {g'(z_0)} \right\rvert}\) (contrapositive to earlier step).
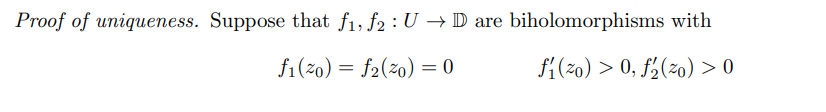
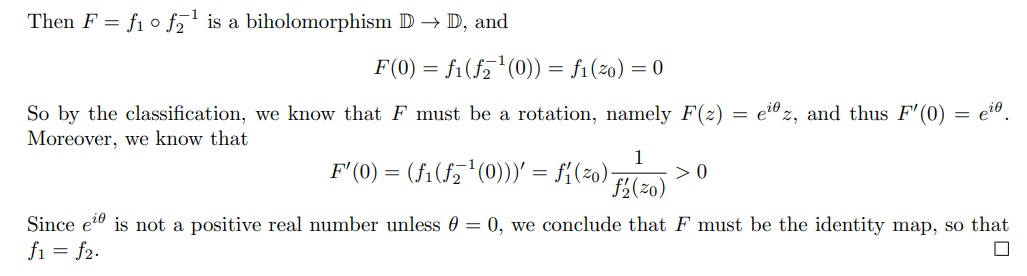


A simply connected nonempty domain \(\Omega \subseteq {\mathbb{C}}\) is conformally equivalent to exactly one of
- \({\mathbb{CP}}^1\),
- \({\mathbb{C}}\), or
- \({\mathbb{D}}\).
Prove that if \(f:U\to V\) is holomorphic and injective then \(f'(z)\neq 0\) on \(U\).
-
Idea: Rouché to get multiple roots, and translate a bit to make sure they’re distinct.
-
Toward a contradiction suppose \(f'(z_0)=0\).
-
Taylor expand and rearrange: \begin{align*} f(z) &= f(z_0) + f'(z_0)(z-z_0) + f''(z_0)(z-z_0)^2 + \cdots \\ \implies f(z) - f(z_0) &= \sum_{j\geq 1} f^{(j)}(z_0)(z-z_0)^j = a(z-z_0)^k + (z-z_0)^{k+1}H(z) ,\end{align*} where \(k\geq 2\) is the first nonvanishing derivative and \(a\coloneqq f^{(k)}(z_0)\).
-
So we can write \begin{align*} f(z) - f(z_0) \coloneqq F_1(z) + G(z) && F_1(z) \coloneqq f^{(k)}(z_0)(z-z_0)^k ,\end{align*} where \(G\) vanishes to order at least \(k+1\) near \(z_0\).
-
For \({\left\lvert {z-z_0} \right\rvert}\) small, note that \(\deg F_1 = k\) and \(\deg G \geq k+1\), so there is some neighborhood \(N\) about \(z_0\) where \({\left\lvert {F_1(z)} \right\rvert} > {\left\lvert {G(z)} \right\rvert}\).
-
Subtract off a small \(w\): \begin{align*} f(z) - f(z_0) - w = F(z) + G(z) && F(z) \coloneqq a(z-z_0)^k - w .\end{align*}
Since \({\left\lvert {F_1} \right\rvert} > {\left\lvert {G} \right\rvert}\), picking \(w\) small enough preserves this inequality, so \({\left\lvert {F} \right\rvert} > {\left\lvert {G} \right\rvert}\) on \(N\).
-
Apply Rouché: \({\sharp}Z(F) = {\sharp}Z(F+G) = {\sharp}Z(f(z) - f(z_0) - w)\).
-
But \(F(z) = a(z-z_0)^k - w\) has exactly \(k\) zeros, and \(k\geq 2\). It only remains to check if they are distinct: \(F'(z) = f'(z)\), and the claim is that we can choose a small enough neighborhood \(N'\) of \(z_0\) so that \(f'(z)\neq 0\) for \(z\neq z_0\), so \(F\) and \(f\) have distinct roots here. This would contradict injectivity.
-
Toward a contradiction, suppose no such \(N'\) exists. Form a sequence of shrinking neighborhoods \(N_j\) about \(z_0\).
-
For each \(N_j\), find a \(z_j\) and \(w_j\) such that \(f(z_j) - w_j = 0\), so \(f(z_j) = w_j\) with multiplicity at least 2 and \(f'(z_j) = 0\).
-
Choose them so that \({\left\lvert {w_{j+1}} \right\rvert} < {\left\lvert {w_j} \right\rvert}\) so \(\left\{{w_j}\right\}\to 0\). But then \(\left\{{z_j}\right\}\to z_0\) with the \(z_j\) distinct, making it a set with an accumulation point. By the identity principal, \(f' \equiv 0\), again contradicting injectivity.
If \(f:U\to V\) is holomorphic and injective, then \(f\) is invertible on its image.
- Idea: show that the usual formula from Calculus will work by defining \((f^{-1})'\) directly.
- By the proposition, \(f'(z) \neq 0\) for \(z\neq z_0\) in \(U\).
- Write \(g\coloneqq f^{-1}\) on \(\operatorname{im}f\), and without loss of generality, replace \(V\) by \(\operatorname{im}f\).
- For \(w, w_0\in V\) with \(0 < {\left\lvert {w-w_0} \right\rvert}\) small, write \(w = f(z)\) and \(w_0 = f(z_0)\) for \(z, z_o\in U\).
- Check the formula for \(g'(w_0)\) and use that \(f'(z_0)\neq 0\): \begin{align*} \frac{g(w)-g\left(w_{0}\right)}{w-w_{0}}=\frac{1}{\frac{w-w_{0}}{g(w)-g\left(w_{0}\right)}}=\frac{1}{\frac{f(z)-f\left(z_{0}\right)}{z-z_{0}}} \overset{z\to z_0}\longrightarrow {1\over f'(z_0) } = {1\over f'(g(w_0))} .\end{align*}