Transforms
\begin{align*} \widehat{f}(\xi) \coloneqq\int_{\mathbb{R}}e^{-i\xi x} f(x)\,dx\\ f(x) = {1\over 2\pi}\int_{\mathbb{R}}e^{i\xi x} \widehat{f}(\xi) \,d\xi .\end{align*}

The Gamma Function
\begin{align*} \Gamma(z) = \int_0^\infty t^{z-1}e^{-t} \,dt .\end{align*}
Some interesting properties of \(\Gamma\): \(\Gamma(z+1) = z\Gamma(z)\) and has simple poles at \(z=0,-1,-2,\cdots\) with residues \(\mathop{\mathrm{Res}}_{z=-m} \Gamma(z) = (-1)^m/m!\). There is also a factorization \begin{align*} \Gamma(z) = {1 \over ze^{\gamma z} \prod_{n=1}^\infty \qty{1 + {z\over n}}e^{-z\over n} } \end{align*} where \(\gamma \coloneqq\lim_{N\to\infty } \sum_{n=1^N} {1\over n} - \log(N)\)
\begin{align*} \Gamma(z) \Gamma(1-z) = {\pi \over \sin(\pi z)} ,\end{align*} which yields a product factorization for \(\sin(\pi z)\).
\({\mathcal{L}}(t^{z-1}, s=1) = \Gamma(z)\) and \({\mathcal{L}}(t^n, s=1) = \Gamma(n+1)\).
The residues:
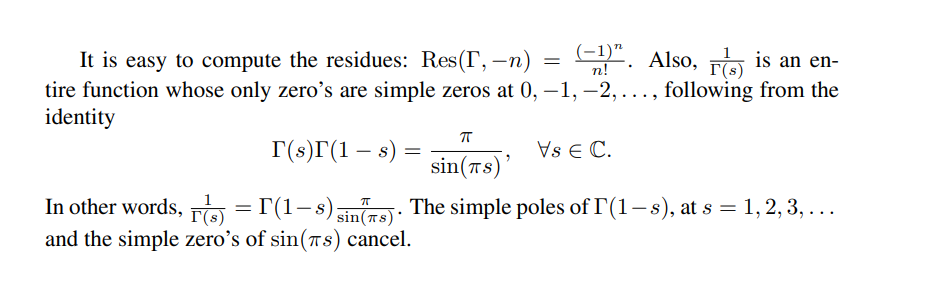

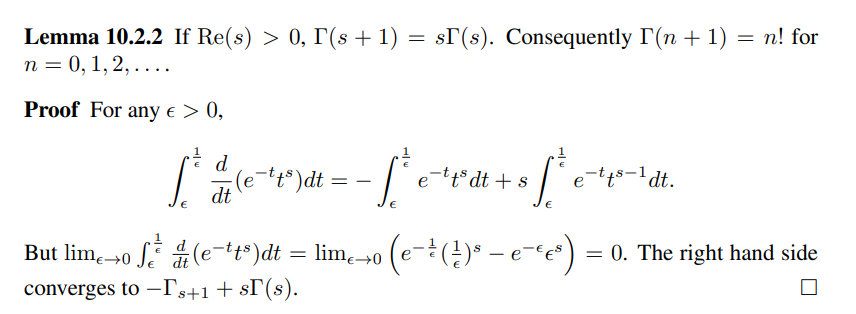

The Beta Function
\begin{align*} B(z, w)=\int_{0}^{1} t^{z-1}(1-t)^{w-1} \mathrm{~d} t .\end{align*}
Show that \begin{align*} B(z, w) = {\Gamma(z) \Gamma(w) \over \Gamma(z+w)} .\end{align*}
Hint: find \({\mathcal{L}}(t^{z-1})\) and \({\mathcal{L}}(t^{z-1}\ast t^{w-1})\).
Riemann Zeta
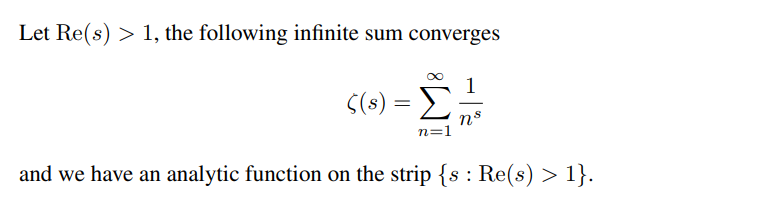
There is a product expansion \begin{align*} \zeta(s) = \prod_{p\in \operatorname{Spec}{\mathbb{Z}}} {1\over 1-p^{-s}} ,\end{align*} where \(\operatorname{Spec}{\mathbb{Z}}\) are the primes of \({\mathbb{Z}}\).

There is a functional equation:
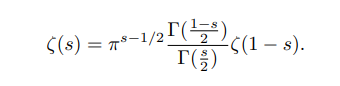

Weierstrass \(\wp\)


Elliptic Functions
Infinite Series and Products
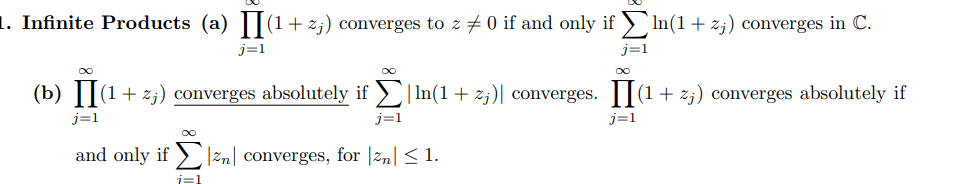
Write \begin{align*} E_{p}(z)= \begin{cases} 1-z & n=0 \\ (1-z) \exp \left(z+\frac{z^{2}}{2}+\cdots+\frac{z^{n}}{n}\right) & \text { otherwise } \end{cases} ,\end{align*} and define the order of an entire function \(f\) to be the infimum over \(p\) where there exists some \(R\) such that \({\left\lvert {f(z)} \right\rvert} \leq e^{{\left\lvert {z} \right\rvert}^p}\) for \({\left\lvert {z} \right\rvert} > R\). Suppose \(f\) is entire of order \(p\), write \(\left\{{z_k}\right\}_{k\leq n}\) for its set of nonzero zeros repeated with multiplicity, and suppose \(z=0\) is a zero of \(f\) of order \(m\). Then there is a decomposition \begin{align*} f(z) = z^m e^{g(z)}\prod_{k\geq 1} E_p\qty{z\over z_k} ,\end{align*} where \(\deg(g) \leq p\).
Find a Hadamard expansion of \(\sin(\pi z)\).
\(\sin(\pi z)\) has order 1, and its zero set is \(z_k = k\) for \(k\in {\mathbb{Z}}\). So one can write \begin{align*} \sin(\pi z) = ze^{az+b} \prod_{k\in {\mathbb{Z}}\setminus\left\{{0}\right\}} \qty{1 - {z\over k}}e^{z\over k} = ze^{az+b} \prod_{k\geq 1}\qty{1 - {z^2\over k^2}} .\end{align*} Determine \(e^b = \pi\) by considering \(\sin(\pi z)/z\) as \(z\to 0\), and use that \(\sin(\pi z)\) is odd and the product factor is even to conclude \(e^{az}\) is even and thus equal to 1. This yields \begin{align*} \sin(\pi z) = \pi z \prod_{k\geq 1}{1- {z^2\over k^2}} .\end{align*}
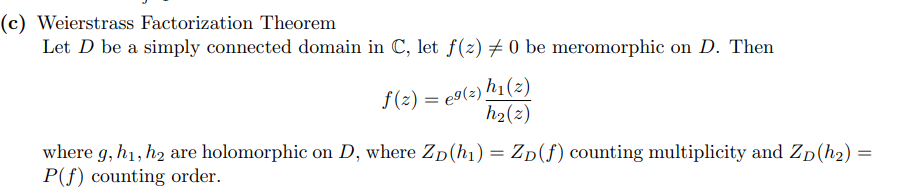
An interesting way to sum infinite series:
\begin{align*} \sum_{n=-\infty}^{\infty} f(n) &=-(\operatorname{sum} \quad \text { of } \quad \text { residues } \quad \text { of } \quad \pi \cot \pi z f(z)) \\ \sum_{n=-\infty}^{\infty}(-1)^{n} f(n) &=-(\operatorname{sum} \quad \text { of } \quad \text { residues } \quad \text { of } \quad \pi \csc \pi z f(z)) \\ \sum_{n=-\infty}^{\infty} f\left(\frac{2 n+1}{2}\right) &=(\operatorname{sum} \quad \text { of } \quad \text { residues of } \quad \pi \tan \pi z f(z)) \\ \sum_{n=-\infty}^{\infty}(-1)^{n} f\left(\frac{2 n+1}{2}\right) &=(\operatorname{sum} \quad \text { of residues of } \pi \sec \pi z f(z)) . .\end{align*}
Show that \begin{align*} \sum_{k\in {\mathbb{Z}}}{1\over (z-k)^2} = (\pi \csc(\pi z))^2 .\end{align*}
Show \begin{align*} \sum_{n \geq 1} \frac{1}{n^{2}}=\frac{\pi^{2}}{6} \end{align*} by integrating \(\pi \cot(\pi z)z^{-2}\).
Show that \begin{align*} \sum_{k\in {\mathbb{Z}}} {1\over k^2 + a^2} = {\pi \coth(\pi a) \over a} \qquad\text{for } a>0 .\end{align*}
Show that \begin{align*} \sum_{k\geq 1}{1\over k^2 + a^2} = {1\over 2}{\pi \coth(\pi a)\over a} - {1\over 2a^2} \qquad a>0 .\end{align*}
Show that \begin{align*} \sum_{k\in {\mathbb{Z}}} {1\over \qty{ k - {1\over 2}}^2 } = \pi^2 .\end{align*}
Show that \begin{align*} \sim_{k\in {\mathbb{Z}}} { (-1)^k \over (k+a)^2} = \pi^2 \cos(\pi a)\csc^2(\pi a) && \text{for } a\in {\mathbb{R}}\setminus{\mathbb{Z}} .\end{align*}
By computing \begin{align*} {1\over 2\pi i}\oint {\cot(\pi z)\over z^2}\,dz ,\end{align*} say using a large rectangle, show that \begin{align*} \zeta(2) = \sum_{k\geq 0} {1\over k^2} = {\pi^2\over 6} .\end{align*}