Show that if \(f_k\to f\) uniformly on \(\Omega\) with \(f_k\) holomorphic then \(f\) is holomorphic.
Alternatively,

Show that if \(f_k \to f\) uniformly with \(f\) holomorphic then every \(n\)th derivative satisfies \(f_k^{(n)}\to f^{(n)}\) uniformly.
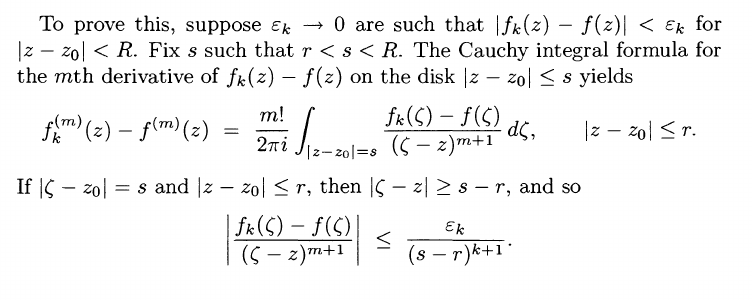
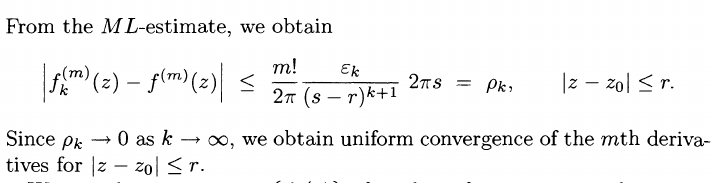
Alt:

Show that if \(f\) is holomorphic on \({\mathbb{D}}\) then \(f\) has a power series expansion that converges uniformly on every compact \(K\subset {\mathbb{D}}\).
Show that any holomorphic function \(f\) can be uniformly approximated by polynomials.
Show that if \(f\) is holomorphic on a connected region \(\Omega\) and \(f'\equiv 0\) on \(\Omega\), then \(f\) is constant on \(\Omega\).
Show that if \({\left\lvert {f} \right\rvert} = 0\) on \({{\partial}}\Omega\) then either \(f\) is constant or \(f\) has a zero in \(\Omega\).
Show that if \(\left\{{f_n}\right\}\) is a sequence of holomorphic functions converging uniformly to a function \(f\) on every compact subset of \(\Omega\), then \(f\) is holomorphic on \(\Omega\) and \(\left\{{f_n'}\right\}\) converges uniformly to \(f'\) on every such compact subset.
Show that if each \(f_n\) is holomorphic on \(\Omega\) and \(F \coloneqq\sum f_n\) converges uniformly on every compact subset of \(\Omega\), then \(F\) is holomorphic.
Show that if \(f\) is once complex differentiable at each point of \(\Omega\), then \(f\) is holomorphic.
Polynomials
Show that if \(f\) is entire and \(f(z) \overset{z\to\infty}\longrightarrow \infty\) then \(f\) is a polynomial.
- Set \(g(z) \coloneqq f(1/z)\), so \(g(z) \overset{z\to 0}\longrightarrow \infty\) making \(z=0\) a singularity.
- This is not an essential singularity by Casorati-Weierstrass.
- So this is a pole and \(g(z) = \sum_{-N\leq k \leq 0} c_k z^k\) for \(N\) the order of the pole
- Thus \(f(z) = \sum_{0<k<N}c_k z^k\) is a polynomial.