Some Geometry
Let \(z_{k}(k=1, \cdots, n)\) be complex numbers lying on the same side of a straight line passing through the origin. Show that
\begin{align*} z_{1}+z_{2}+\cdots+z_{n} \neq 0, \quad 1 / z_{1}+1 / z_{2}+\cdots+1 / z_{n} \neq 0 \end{align*}
Hint: Consider a special situation first.
Images of circles
Let \(f(z)=z+1 / z\). Describe the images of both the circle \(|z|=r\) of radius \(r(r \neq 0)\) and the ray \(\arg z=\theta_{0}\) under \(f\) in terms of well known curves.
Geometric Identities
Prove that \(\left|z_{1}+z_{2}\right|^{2}+\left|z_{1}-z_{2}\right|^{2}=2\left(\left|z_{1}\right|^{2}+\left|z_{2}\right|^{2}\right)\) for any two complex numbers \(z_{1}, z_{2}\), and explain the geometric meaning of this identity
Geometric Identities
Use \(n\)-th roots of unity (i.e. solutions of \(z^{n}-1=0\) ) to show that
\begin{align*} \cos \frac{2 \pi}{n}+\cos \frac{4 \pi}{n}+\cos \frac{6 \pi}{n}+\cdots+\cos \frac{2(n-1) \pi}{n}+=-1 \text { and } \\ \sin \frac{2 \pi}{n}+\sin \frac{4 \pi}{n}+\sin \frac{6 \pi}{n}+\cdots \frac{2(n-1) \pi}{n}=0 \end{align*}
Hint: If \(z^{n}+c_{1} z^{n-1}+\cdots+c_{n-1} z+c_{n}=0\) has roots \(z_{1}, z_{2}, \ldots, z_{n}\), then \begin{align*} z_{1}+z_{2}+\cdots+z_{n}=-c_{1} \\ z_{1} z_{2} \cdots z_{n}=(-1)^{n} c_{n} \text { (not used) } \end{align*}
Geometry from equations
Describe each set in the \(z\)-plane in (a) and (b) below, where \(\alpha\) is a complex number and \(k\) is a positive number such that \(2|\alpha|<k\).
-
\(|z-\alpha|+|z+\alpha|=k\);
-
\(|z-\alpha|+|z+\alpha| \leq k\).
Spring 2020.1, Spring 2020 HW 1.4 #complex/qual/completed
-
Prove that if \(c>0\), \begin{align*} {\left\lvert {w_1} \right\rvert} = c{\left\lvert {w_2} \right\rvert} \implies {\left\lvert {w_1 - c^2 w_2} \right\rvert} = c{\left\lvert {w_1 - w_2} \right\rvert} .\end{align*}
-
Prove that if \(c>0\) and \(c\neq 1\), with \(z_1\neq z_2\), then the following equation represents a circle: \begin{align*} {\left\lvert {z-z_1 \over z-z_2} \right\rvert} = c .\end{align*} Find its center and radius.
Hint: use part (a)
\begin{align*} {\left\lvert {w_1 - c^2 w_2} \right\rvert}^2 &= (w_1 - c^2 w_2) ( \mkern 1.5mu\overline{\mkern-1.5muw_1\mkern-1.5mu}\mkern 1.5mu - c^2 \mkern 1.5mu\overline{\mkern-1.5muw_2\mkern-1.5mu}\mkern 1.5mu ) \\ &= {\left\lvert {w_1} \right\rvert}^2 + c^4 {\left\lvert {w_2} \right\rvert}^2 - 2c^2 \Re(w_1 \mkern 1.5mu\overline{\mkern-1.5muw_2\mkern-1.5mu}\mkern 1.5mu) \\ &= {\color{green} c^2 {\left\lvert {w_2} \right\rvert}^2 } + c^4 {\left\lvert {w_2} \right\rvert}^2 - 2c^2 \Re(w_1 \mkern 1.5mu\overline{\mkern-1.5muw_2\mkern-1.5mu}\mkern 1.5mu) \\ &= c^2 {\left\lvert {w_2} \right\rvert}^2 + {\color{green} c^2 {\left\lvert {w_1} \right\rvert}^2 } - 2c^2 \Re(w_1 \mkern 1.5mu\overline{\mkern-1.5muw_2\mkern-1.5mu}\mkern 1.5mu) \\ &= c^2 {\left\lvert {w_1 - w_2} \right\rvert} ,\end{align*} where we’ve applied the assumption \({\left\lvert {w_1} \right\rvert} = c{\left\lvert {w_2} \right\rvert}\) twice.
Using part 1: \begin{align*} w_1\coloneqq z-z_1, w_2 \coloneqq z-z_2 \implies {\left\lvert {w_1} \right\rvert} &= c{\left\lvert {w_2} \right\rvert} \\ \implies {\left\lvert {w_1 - c^2 w_2} \right\rvert} &= c {\left\lvert {w_1 - w_2} \right\rvert} \\ \implies {\left\lvert { z-z_1 - c^2 (z-z_2) } \right\rvert} &= {\left\lvert {(z-z_1) - (z-z_2)} \right\rvert} \\ \implies {\left\lvert {(1-c^2) z - z_3} \right\rvert} &= {\left\lvert { z_2 - z_1 } \right\rvert} \\ \implies {\left\lvert {z-z_4} \right\rvert} &= r ,\end{align*} where the \(z_i\) and \(r\) are all constant, so this is the equation of a circle.
Spring 2020 HW 1.1 #complex/exercise/completed
Geometrically describe the following subsets of \({\mathbb{C}}\):
- \({\left\lvert {z-1} \right\rvert} = 1\)
- \({\left\lvert {z-1} \right\rvert} = 2{\left\lvert {z-2} \right\rvert}\)
- \(1/z = \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu\)
- \(\Re(z) = 3\)
- \(\Im(z) = a\) with \(a\in {\mathbb{R}}\).
- \(\Re(z) > a\) with \(a\in {\mathbb{R}}\).
- \({\left\lvert {z-1} \right\rvert} < 2{\left\lvert {z-2} \right\rvert}\)
-
A circle of radius 1 about \(z=1\).
-
A circle, using that Apollonius circles are characterized as the locus of distances whose ratios to some fixed points \(A, B\) are constant. To actually compute this: \begin{align*} {\left\lvert {z-1} \right\rvert}^2 &= 4{\left\lvert {z-2} \right\rvert}^2 \\ \implies (x-1)^2 + y^2 - 4\qty{(x-2)^2 + y^2 } &=0 \\ -3x^2 + 14x - 3y^2 - 15 &= 0 && \star\\ \implies x^2 - {14\over 3}x + y^2 + 5 &= 0 \\ \implies (x- {14\over 2\cdot 3})^2 - {14\over 2\cdot 3}^2 + y^2 + 5 &= 0 \\ \implies (x-{14\over 6})^2 + y^2 = \qty{2\over 3}^2 ,\end{align*} which is a circle of radius \(2/3\) with center \(\qty{{14\over 6}, 0}\). To avoid the calculation, use \begin{align*} Ax^2 + Bxy + Cy + \cdots = 0,\quad A=1, B=0, C=1 \implies \Delta \coloneqq B^2 - 4AC < 0 ,\end{align*} which is an ellipse, and since \(A=C\) it is in fact a circle.
-
\(S^1\), using that \({1\over z} = {\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu \over z\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu} = {\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu\over {\left\lvert {z} \right\rvert}^2}\) and if this equals \(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu\), then \({\left\lvert {z} \right\rvert}^2=1\). Alternatively, \(1 = \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5muz = {\left\lvert {z} \right\rvert}^2\).
-
Vertical line through \(z=3\).
-
Horizontal line through \(z=ia\).
-
Region to the right of the vertical line through \(z=a\).
-
Exterior of a circle: same calculation is (2), replacing \(=0\) with \(<0\). Note that the line marked \(\star\) involves dividing by a negative, so this flips the sign, and we get \(\cdots > \qty{2\over 3}^2\) at the end.
Fixed argument exercise #complex/exercise/completed
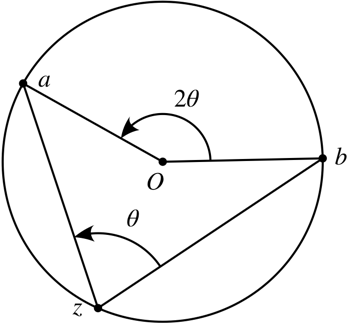
Fix \(a,b\in {\mathbb{C}}\) and \(\theta\), and describe the locus \begin{align*} \left\{{z{~\mathrel{\Big\vert}~}\operatorname{Arg}\qty{z-a\over z-b} = \theta}\right\} .\end{align*}
The geometry at hand:
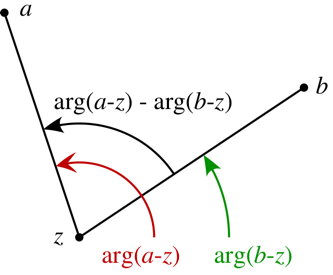
By the inscribed angle theorem, this locus is an arc of a circle whose center \(O\) is the point for which the angle \(aOb\) is \(2\theta\):
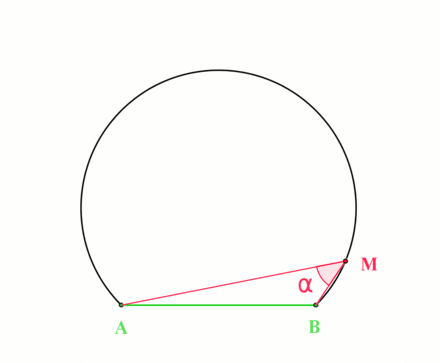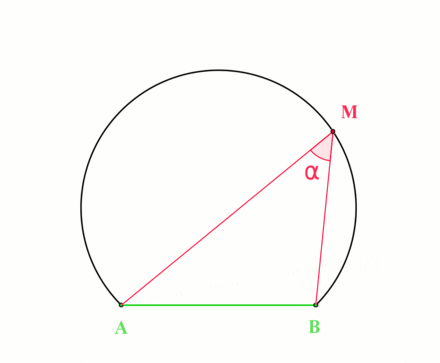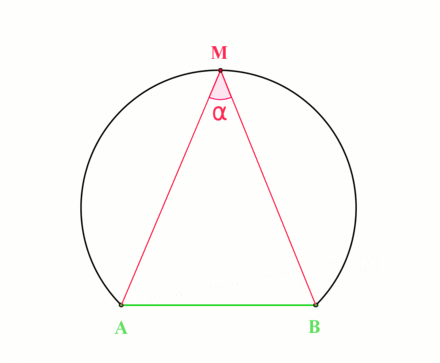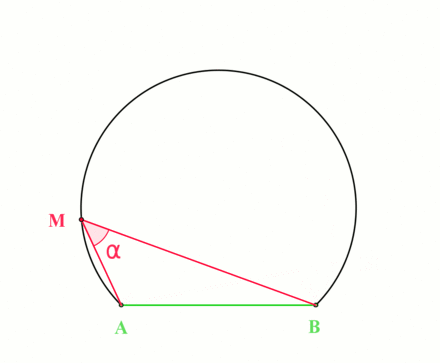
Fall 2019.2, Spring 2020 HW 1.11 #complex/qual/completed
Prove that the distinct complex numbers \(z_1, z_2, z_3\) are the vertices of an equilateral triangle if and only if \begin{align*} z_{1}^{2}+z_{2}^{2}+z_{3}^{2}=z_{1} z_{2}+z_{2} z_{3}+z_{3} z_{1} .\end{align*}
\(\implies\): Write the vertices as \(z_1, z_2, z_3\) and the sides as
- \(s_1 \coloneqq z_2-z_1\)
- \(s_2 \coloneqq z_3 - z_2\)
- \(s_1 \coloneqq z_1 -z_3\)
Note that \(s_i = \pm \zeta_3 s_{i-1}\), dividing yields \begin{align*} {s_2 \over s_3} &= {s_1\over s_2} \\ &\iff s_2^2 - s_1 s_3 = 0 \\ &\iff \left(z_{2}-z_{3}\right)^{2}-\left(z_{2}-z_{1}\right)\left(z_{1}-z_{3}\right)=0 \\ &\iff \left(z_{2}^{2}+z_{3}^{2}-2 z_{2} z_{3}\right)-\left(z_{2} z_{1}-z_{2} z_{3}-z_{1}^{2}+z_{1} z_{3}\right)=0 \\ &\iff z_{1}^{2}+z_{2}^{2}+z_{3}^{2}-\left(z_{1} z_{2}+z_{2} z_{3}+z_{3} z_{1}\right)=0 .\end{align*}
\(\impliedby\): We still have \(s_i = \theta_i s_{i-1}\) for some angles \(\theta_i\) We have
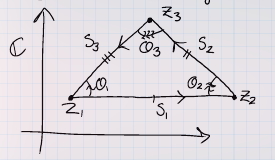
and \begin{align*} {s_1\over s_2} &= {\theta_1 \over \theta_2} \cdot {s_3\over s_1} \\ {s_2\over s_3} &= {\theta_2 \over \theta_3} \cdot {s_1\over s_2} \\ {s_3\over s_1} &= {\theta_3 \over \theta_1} \cdot {s_2\over s_3} .\end{align*}
Running the above calculation backward yields \(s_2/s_3 = s_1/s_2\), and by the 2nd equality above, this forces \(\theta_2 = \theta_3\). Similar arguments show \(\theta_1=\theta_2 = \theta_3\) which forces \(s_1=s_2 = s_3\).
Complex Arithmetic
Sum of Sines
Use de Moivre’s theorem (i.e. \(\left(e^{i \theta}\right)^{n}==\cos n \theta+i \sin n \theta\), or \(\left.(\cos \theta+i \sin \theta)^{n}=\cos n \theta+i \sin n \theta\right)\) to find the sum
\begin{align*} \sin x+\sin 2 x+\cdots+\sin n x \end{align*}
Solving Equations
Characterize positive integers \(n\) such that \((1+i)^{n}=(1-i)^{n}\)
Characters
Let \(n\) be a natural number. Show that
\begin{align*} [1 / 2(-1+\sqrt{3} i)]^{n}+[1 / 2(-1-\sqrt{3} i)]^{n} \end{align*}
is equal to 2 if \(n\) is a multiple of 3 , and it is equal to \(-1\) otherwise.
Spring 2019.3 #complex/qual/stuck
Let \(R>0\). Suppose \(f\) is holomorphic on \(\left\{{z{~\mathrel{\Big\vert}~}{\left\lvert {z} \right\rvert} < 3R}\right\}\). Let \begin{align*} M_{R}:=\sup _{|z| \leq R}|f(z)|, \quad N_{R}:=\sup _{|z| \leq R}\left|f^{\prime}(z)\right| \end{align*}
-
Estimate \(M_{R}\) in terms of \(N_{R}\) from above.
-
Estimate \(N_{R}\) in terms of \(M_{2 R}\) from above.
First note that by the maximum modulus principal, it suffices to consider sups on the boundary, i.e. \begin{align*} M_R = \sup_{{\left\lvert {z} \right\rvert} = R}{\left\lvert {f(z)} \right\rvert}, \qquad N_R = \sup_{{\left\lvert {z} \right\rvert} = R} {\left\lvert {f'(z)} \right\rvert} .\end{align*}
The first estimate: stuck!
The second estimate: suppose \(z_0 \in {\mathbb{D}}_R(0)\), then any \(D_R(z_0)\) is contained in \(D_{2R}(0)\), So for any such \(z_0\), apply Cauchy’s integral formula centered at \(z_0\): \begin{align*} f^{(1)}(z_0) &= {1\over 2\pi i }\oint_{{{\partial}}{\mathbb{D}}_{R}(z_0)} {f(\xi)\over (\xi-z_0)^2 }\,d\xi\\ \implies {\left\lvert { f^{(1)}(z_0)} \right\rvert} &\leq {1\over 2\pi} \oint_{{{\partial}}{\mathbb{D}}_{R}(z_0)} {\left\lvert {f(\xi)\over (\xi-z_0)^2 } \right\rvert}\,d\xi\\ &= {1\over 2\pi} \oint_{{{\partial}}{\mathbb{D}}_R(z_0)} { {\left\lvert {f(\xi)} \right\rvert} \over {\left\lvert {\xi-z_0} \right\rvert}^2 } \,d\xi\\ &= {1\over 2\pi} \oint_{{{\partial}}{\mathbb{D}}_R(z_0)} { {\left\lvert {f(\xi)} \right\rvert} \over R^2 } \,d\xi\\ &\leq {1\over 2\pi} R^{-2} \oint_{{{\partial}}{\mathbb{D}}_R(z_0)} { \sup_{z\in {{\partial}}{\mathbb{D}}_{R}(z_0) } {\left\lvert {f(z)} \right\rvert} } \,d\xi\\ &= {1\over 2\pi} R^{-2} \sup_{{{\partial}}{\mathbb{D}}_R(z_0) } {\left\lvert {f(z)} \right\rvert} \cdot 2\pi R \\ &= R^{-1}\sup_{{{\partial}}{\mathbb{D}}_R(z_0) } {\left\lvert {f(z)} \right\rvert} \\ &\leq R^{-1}M_{2R} ,\end{align*} where we’ve used in the last step that \({\mathbb{D}}_R(z_0) \subseteq {\mathbb{D}}_{2R}(0)\), and sups can only get larger when taken over larger sets. Since this was an arbitrary \(z_0\in {\mathbb{D}}_R(0)\), this holds for all \(z\) with \({\left\lvert {z} \right\rvert} \leq R\). Since taking sups preserves inequalities, we have \begin{align*} {\left\lvert {f'(z_0)} \right\rvert} \leq R^{-1}M_{2R}\, \forall {\left\lvert {z} \right\rvert} \leq R \implies N_R\coloneqq\sup_{{\left\lvert {z} \right\rvert} \leq R}{\left\lvert {f'(z)} \right\rvert} \leq R^{-1}M_{2R} .\end{align*}
Spring 2021.1 #complex/qual/completed
The question as written on the original qual has several errors. What is below is the correct version of the inequality.
- Let \(z_{1}\) and \(z_{2}\) be two complex numbers.
-
Show that \begin{align*} \left|1-\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu_{1} z_{2}\right|^{2}-\left|z_{1}-z_{2}\right|^{2}=\left(1-\left|z_{1}\right|^{2}\right)\left(1-\left|z_{2}\right|^2\right) \end{align*}
-
Show that if \(\left|z_{1}\right|<1\) and \(\left|z_{2}\right|<1\), then \(\left|\frac{z_{1}-z_{2}}{1-\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu_{1} z_{2}}\right|<1 .\)
- Assume that \(z_{1} \neq z_{2}\). Show that \(\left|\frac{z_{1}-z_{2}}{1-\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu_{1} z_{2}}\right|=1\) if only if \(\left|z_{1}\right|=1\) or \(\left|z_{2}\right|=1\).
Part 1: For ease of notation, let \(z=z_1\) and \(w=z_2\) We want to show \begin{align*} {\left\lvert {1- z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu} \right\rvert} - {\left\lvert {z-w} \right\rvert}^2 = \qty{{1 - {\left\lvert {z} \right\rvert}^2 }} \qty{{1 - {\left\lvert {w} \right\rvert}^2}} .\end{align*}
So write \begin{align*} {\left\lvert {1- z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu} \right\rvert} - {\left\lvert {z-w} \right\rvert}^2 &= (1-z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu)(1-\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w) - (z-w)(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu) \\ &= 1 - z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu - \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w - {\left\lvert {z} \right\rvert}^2{\left\lvert {w} \right\rvert}^2 - {\left\lvert {z} \right\rvert}^2 - {\left\lvert {w} \right\rvert}^2 + w\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu + z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu \\ &= 1 - {\left\lvert {z} \right\rvert}^2{\left\lvert {w} \right\rvert}^2 - {\left\lvert {z} \right\rvert}^2 - {\left\lvert {w} \right\rvert}^2 \\ &=(1-{\left\lvert {z} \right\rvert}^2)(1-{\left\lvert {w} \right\rvert}^2) .\end{align*}
Part 2 and 3: \begin{align*} {\left\lvert {z-w \over 1 - \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w} \right\rvert}^2 \leq 1 &\iff 0 \leq {\left\lvert {1 - \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w} \right\rvert}^2 - {\left\lvert {z-w} \right\rvert}^2 \\ &\iff 0 \leq (1 - {\left\lvert {z} \right\rvert}^2 )(1 - {\left\lvert {w} \right\rvert}^2) ,\end{align*} where we’ve used part 1. But this is clearly true when \({\left\lvert {z} \right\rvert}, {\left\lvert {w} \right\rvert} < 1\), so the RHS is positive. Moreover if \({\left\lvert {z} \right\rvert} = {\left\lvert {w} \right\rvert} = 1\), the RHS is zero, yielding equalities at every step instead.
Spring 2020 HW 1.5 #complex/qual/completed
-
Let \(z, w \in {\mathbb{C}}\) with \(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w \neq 1\). Prove that \begin{align*} {\left\lvert {w-z \over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} < 1 \quad\text{ if } {\left\lvert {z} \right\rvert}<1,~ {\left\lvert {w} \right\rvert} < 1 \end{align*} with equality when \({\left\lvert {z} \right\rvert} = 1\) or \({\left\lvert {w} \right\rvert} = 1\).
-
Prove that for a fixed \(w\in {\mathbb{D}}\), the mapping \(F: z\mapsto {w-z \over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}\) satisfies
- \(F\) maps \({\mathbb{D}}\) to itself and is holomorphic.
- \(F(0) = w\) and \(F(w) = 0\).
- \({\left\lvert {z} \right\rvert} = 1\) implies \({\left\lvert {F(z)} \right\rvert} = 1\).
- \(F\) is a bijection.
Part 1: See Spring 2021.1 above.
Part 2, holomorphicity: This is clearly meromorphic, as it’s a rational function, and has a singularity only at \(z\) such that \(\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z = 1\). This can only happen if \(z, w \in S^1\): taking the modulus yields \begin{align*} \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z = 1 \implies {\left\lvert {w} \right\rvert}^2{\left\lvert {z} \right\rvert}^2 = 1 ,\end{align*} and moreover since \({\left\lvert {w} \right\rvert}^2 \leq 1\) and \({\left\lvert {z} \right\rvert}^2\leq 1\), the only way this product can be one is when \({\left\lvert {w} \right\rvert}^2 = {\left\lvert {z} \right\rvert}^2 = 1\). This also forces \(z=1/\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu\).
The claim is that the singularity \(1/\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu\) is removable. Note that \(1\over w = \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu\) on the circle, so \(1/\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu = \mkern 1.5mu\overline{\mkern-1.5mu\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu\mkern-1.5mu}\mkern 1.5mu = 2\), so \begin{align*} \qty{ z- \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu^{-1}} \qty{w-z \over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} &= \qty{\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z - 1 \over \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu} \qty{w-z \over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \\ &= \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu^{-1}(w-z) \\ &= w(w-z) \\ &\overset{z\to \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu^{-1}=w }\to 0 .\end{align*}
Part 2, being a bijection: This follows from finding an explicit inverse, using that \(F^2 = \operatorname{id}\): \begin{align*} F(F(z)) &= \frac{w- \qty{ \frac{w-z}{1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} } }{1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu \qty{ \frac{w-z}{1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} } } \\ &= \frac{w(1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z)-(w-z)}{q-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu(w-z)} \\ &= \frac{w-|w|^{2} z-w+z}{1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z-|w|^{2}+\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \\ &= \frac{z\left(1-|w|^{2}\right)}{1-|w|^{2}} \\ &= z .\end{align*}
Part 2, being an involution: A direct check shows that \(F(w) = 0\), since the numerator vanishes, and \(F(0) = {w - 0 \over 1 - 0} = w\).
Part 3, preserving the circle: Follows from the estimate in part 1.
Spring 2020 HW 1.2 #complex/qual/completed
Prove the following inequality, and explain when equality holds: \begin{align*} {\left\lvert {z-w} \right\rvert} \geq {\left\lvert { {\left\lvert {z} \right\rvert} - {\left\lvert {w} \right\rvert} } \right\rvert} .\end{align*}
\begin{align*} {\left\lvert {z-w} \right\rvert}^2 &= (z-w)(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu) \\ &= {\left\lvert {z} \right\rvert}^2 + {\left\lvert {w} \right\rvert}^2 - z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu - \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w \\ &= {\left\lvert {z} \right\rvert}^2 + {\left\lvert {w} \right\rvert}^2 - 2\Re(\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z) \\ &\geq {\left\lvert {z} \right\rvert}^2 + {\left\lvert {w} \right\rvert}^2 - 2{\left\lvert {\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu } \right\rvert}{\left\lvert {z} \right\rvert} \\ &\geq \qty{ {\left\lvert {z} \right\rvert} - {\left\lvert {w} \right\rvert} }^2 ,\end{align*} and taking square roots introduces an absolute value on the final term. Here we’ve used the basic estimate \begin{align*} \Re(z) \leq {\left\lvert {z} \right\rvert} \implies -\Re(z) \geq -{\left\lvert {z} \right\rvert} .\end{align*}
Fall 2020.1, Spring 2020 HW 1.6 #complex/qual/completed
Use \(n\)th roots of unity to show that \begin{align*} 2^{n-1} \sin\qty{\pi \over n} \sin\qty{2\pi \over n} \cdots \sin\qty{(n-1)\pi \over n} = n .\end{align*}
Hint: \begin{align*} 1 - \cos(2\theta) &= 2\sin^2(\theta) \\ 2 \sin(2\theta) &= 2\sin(\theta) \cos(\theta) .\end{align*}
- \(\zeta_n \coloneqq e^{2\pi i \over n}\)
- \(\Phi_n(z) \coloneqq\prod_{1\leq j \leq n-1}(z-\zeta_n^j)\)
- \(\Phi_n(1) = n\), since \(\Phi_n(z) = {z^n-1\over z-1} = \sum_{0\leq j\leq n-1} z^j\).
- \(\sin(z) = \qty{e^{iz} - e^{-iz} \over 2i}\).
- \(\prod_k \exp(c_k) = \exp\qty{\sum_k c_k}\).
\begin{align*} \prod_{1\leq k \leq n-1} \sin\qty{k\pi\over n} &= \prod_{1\leq k \leq n-1} {\omega_n^k - \omega_n^{-k} \over 2i} \\ &= \qty{1\over 2i}^{n-1} \prod_{1\leq k \leq n-1} \omega_n^{k} \qty{1 - \zeta_n^{-k}} \\ &= \qty{1\over 2i}^{n-1} \prod_{1\leq k \leq n-1} \exp\qty{i\pi k\over n} \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{-k}} \\ &= \qty{1\over 2i}^{n-1} \exp\qty{ {i\pi\over n} \displaystyle\sum_{1\leq k \leq n-1} k } \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{-k}} \\ &= \qty{1\over 2i}^{n-1} e^{i\pi n(n-1)\over 2n} \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{-k}} \\ &= \qty{1\over 2}^{n-1}\qty{1\over i}^{n-1} \qty{ e^{i\pi \over 2} }^{n-1} \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{-k}} \\ &= 2^{1-n} \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{-k}} \\ &= 2^{1-n} \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{k}} \\ &= 2^{1-n} { \Phi_n(z) \over z-1}\Big|_{z=1} \\ &= 2^{1-n} \qty{ \sum_{0\leq k \leq n-1} z^k}\Big|_{z=1} \\ &= n2^{1-n} .\end{align*}
\begin{align*} \prod_{1\leq j\leq n-1} \sin \left(\frac{j \pi}{n}\right) &=\prod_{1\leq j\leq n-1} \frac{1}{2 i} \qty{\zeta_n^{j\over 2} - \zeta_n^{- {j \over 2} }} \\ &=\left(\frac{1}{2 i}\right)^{n-1} \prod_{1\leq j\leq n-1} \zeta_n^{j\over 2} \prod_{1\leq j \leq n-1} \qty{1 - \zeta_n^{-j}} \\ &=\left(\frac{1}{2 i}\right)^{n-1} \prod_{1\leq j\leq n-1} \exp\qty{ij\pi \over n} \prod_{1\leq j \leq n-1} \qty{1 - \zeta_n^{-j}} \\ &=\left(\frac{1}{2 i}\right)^{n-1} \exp \left(\sum_{1\leq j\leq n-1} \frac{i j \pi}{n}\right) \Phi_{n}(1)\\ &=\left(\frac{1}{2 i}\right)^{n-1} \exp \left(\frac{(n-1) i \pi}{2}\right) \Phi_{n}(1)\\ &=\left(\frac{1}{2 i}\right)^{n-1}\left(e^{i \pi / 2}\right)^{n-1} \Phi_{n}(1)\\ &=\left(\frac{1}{2 i}\right)^{n-1} i^{n-1} \Phi_{n}(1)\\ &=\left(\frac{1}{2}\right)^{n-1} \Phi_{n}(1)\\ &=\frac{n}{2^{n-1}} .\end{align*}
Spring 2020 HW 1.5 #complex/qual/completed
-
Let \(z, w \in {\mathbb{C}}\) with \(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w \neq 1\). Prove that \begin{align*} {\left\lvert {w-z \over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} < 1 \quad\text{ if } {\left\lvert {z} \right\rvert}<1,~ {\left\lvert {w} \right\rvert} < 1 \end{align*} with equality when \({\left\lvert {z} \right\rvert} = 1\) or \({\left\lvert {w} \right\rvert} = 1\).
-
Prove that for a fixed \(w\in {\mathbb{D}}\), the mapping \(F: z\mapsto {w-z \over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}\) satisfies
- \(F\) maps \({\mathbb{D}}\) to itself and is holomorphic.
- \(F(0) = w\) and \(F(w) = 0\).
- \({\left\lvert {z} \right\rvert} = 1\) implies \({\left\lvert {F(z)} \right\rvert} = 1\).
\begin{align*} 0 &\leq (1 - {\left\lvert {w} \right\rvert}^2)(1-{\left\lvert {z} \right\rvert}^2) \\ \implies {\left\lvert {w} \right\rvert}^2 + {\left\lvert {z} \right\rvert}^2 &\leq 1 + {\left\lvert {w} \right\rvert}^2 {\left\lvert {z} \right\rvert}^2 \\ \implies {\left\lvert {w} \right\rvert}^2 + {\left\lvert {z} \right\rvert}^2 - 2\Re(\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z) &\leq 1 + {\left\lvert {w} \right\rvert}^2 {\left\lvert {z} \right\rvert}^2 - 2\Re(\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z) \\ \implies {\left\lvert {w-z} \right\rvert}^2 &\leq {\left\lvert {1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5muz} \right\rvert}^2 .\end{align*} Note that if either \({\left\lvert {w} \right\rvert}^2 = 1\) or \({\left\lvert {z} \right\rvert}^2 = 1\) then the first line is an equality, yielding equality in the final line.
-
That \(F: {\mathbb{D}}\to {\mathbb{D}}\): follows from the inequality, since \({\left\lvert {z} \right\rvert}, {\left\lvert {w} \right\rvert} < 1\) for \(z,w\in {\mathbb{D}}\). Holomorphicity: follows from the fact that rational expressions of holomorphic functions are holomorphic away from where the denominators vanish.
-
Then just note that \({\left\lvert {\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} \lleq {\left\lvert {w} \right\rvert}{\left\lvert {z} \right\rvert} < 1\), so \({\left\lvert {1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} > 0\).
-
\(F(0) = {w-0 \over 1-0} = w\)
-
\(F(w) = {w-w\over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu w} = 0\)
-
\({\left\lvert {z} \right\rvert} = 1\) yields equality in part 1.
Other notes: \(F\) is bijective on \({\mathbb{D}}\): \begin{align*} F(F(z)) &= {w - \qty{w-z\over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu\qty{w-z\over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} } \\ &= {w(1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z) - (w-z) \over (1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z) - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu (w-z)} \\ &= {z-{\left\lvert {w} \right\rvert}^2 z \over 1 - {\left\lvert {w} \right\rvert}^2 }\\ &= z .\end{align*}