Rational, wedge
Fall 2021.3 #complex/exercise/completed
Suppose \(n \geq 2\). Use a wedge of angle \(\frac{2 \pi}{n}\) to evaluate the integral \begin{align*} I=\int_{0}^{\infty} \frac{1}{1+x^{n}} d x \end{align*}
By the ML estimate, \(\int_{C_R} f \to 0\).
The residue contribution: note the simple pole at \(\omega_n \coloneqq e^{i\pi \over n}\), \begin{align*} \mathop{\mathrm{Res}}_{z=\omega_n} f(z) = {1\over n\omega_n^{n-1}} = {\omega \over n\omega^n} = -{\omega_n \over n} .\end{align*}
The segment contributions: \(\int_{\gamma_1}f\to I\), and \begin{align*} \int_{\gamma_2}f(z) \,dz= \int_\infty^0 {1\over 1 + (\zeta_nt)^n} \zeta_n \,dt= -\zeta_n I ,\end{align*} so the contour contributions sum to \((1-\zeta_n)I\).
Solving: \begin{align*} I = -{2\pi i \omega_n\over n(1-\zeta_n)} = -2\pi i {1\over \omega_n^{-1}- \omega_n} = -2\pi i {1\over 2i \sin\qty{\pi \over n}} = {\pi \over n} \csc\qty{\pi \over n} .\end{align*}
Write \(\omega_{n, k} = \exp\qty{(2k+1)i\pi \over n}\) and factor \(z^n+1\) as \begin{align*} z^n+1 = \prod_{1\leq k \leq n}(z-\omega_{n, k}) = (z-e^{i\pi \over n})(z-e^{3i\pi \over n}) \cdots (z-e^{(2n-1)i\pi \over n}) .\end{align*} Note that only the root \(e^{i\pi\over n}\) lies in the \(2\pi/n\) wedge, so it is the only (simple) pole of \(f(z) \coloneqq{1\over 1+z^n}\) in this region. Since the pole is simple, we can compute the residue easily. Write \(r_0 \coloneqq e^{e\pi\over n}\), then By L’Hopital, \begin{align*} \mathop{\mathrm{Res}}_{z = r_0} {1\over 1+z^n} &= \lim_{z\to r_0} {z-r_0 \over 1 + z^n} \\ &= \lim_{z\to r_0} {1\over nz^{n-1}} \\ &= {1\over nr_0^{n-1}} \\ &= {1\over n e^{i\pi (n-1) \over n}} \\ &= n^{-1}{\exp\qty{-i\pi (n-1)\over n }} .\end{align*}
Take a contour \(\Gamma\) comprised of
- \(\gamma_1 = [0, R] \subseteq {\mathbb{R}}\)
- \(\gamma_2 = \left\{{Re^{it} {~\mathrel{\Big\vert}~}t\in [0, 2\pi/n]}\right\}\)
- \(\gamma_3 = \zeta_n [0, R]\)
By the residue theorem \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=r_0} f(z) = I \coloneqq\int_\Gamma f = \qty{\int_{\gamma_1} + \int_{\gamma_2} + \int_{\gamma_3}}f .\end{align*}
Taking orientations into account, \begin{align*} \int_{\gamma_3} f = -\zeta_n \int_{\gamma_1} f .\end{align*}
\begin{align*} \int_{\gamma_2}f\overset{R\to\infty}\longrightarrow 0 .\end{align*}
so in the limit we have \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=r_0}f(z) &= \qty{1 - \zeta_n}\int_{\gamma_1}f \\ \implies \int_{\gamma_1} f &= {2\pi i \mathop{\mathrm{Res}}_{z=r_0}f(z) \over 1 - \zeta_n}\\ &= {2\pi i e^{-\pi (n-1) \over n} \over n\qty{1-e^{2\pi i \over n}}} \\ &= {2\pi i \over n} \left[ e^{i\pi} e^{-i\pi \over n}\qty{1 - e^{2\pi i \over n}} \right]^{-1}\\ &= {2\pi i \over n} \left[ -1\qty{e^{-i\pi \over n} - e^{\pi i \over n}} \right]^{-1}\\ &= {2\pi i \over n} \left[ 2i \sin\qty{\pi\over n} \right]^{-1}\\ &= {\pi \over n\sin\qty{\pi \over n}} .\end{align*}
Parameterize the curves:
- \(\gamma_1 \coloneqq\left\{{t {~\mathrel{\Big\vert}~}t\in [0, R]}\right\}, \,dz= \,dt\)
- \(\gamma_3 \coloneqq\left\{{t\zeta_n {~\mathrel{\Big\vert}~}t\in [0, R]}\right\}, \,dz= \zeta_n \,dt\)
Then, a direct check: \begin{align*} \int_{\gamma_3}f(z) \,dz &= \int_0^R {1\over 1 + (\zeta_n t)^n}\zeta_n \,dt\\ &= \zeta_n\int_0^R {1\over 1 + t^n}\,dt\\ &= \zeta_n \int_{\gamma_1}f(z) \,dz .\end{align*}
Parameterize \(\gamma_2 = \left\{{Re^{it} {~\mathrel{\Big\vert}~}t\in [0, 2\pi/n]}\right\}\) and apply the ML estimate: \begin{align*} {1\over 1 + (Re^{it})^n} \leq {1\over R^n - 1} \implies \int_{\gamma_2}f \leq {1\over R^n - 1} \qty{{2\pi R \over n}} = { \mathsf{O}} (R^{n-1})\overset{R\to\infty}\longrightarrow 0 .\end{align*}
Spring 2020 HW 3, SS 3.8.2 #complex/exercise/work
Evaluate the integral \begin{align*} \int_\mathbb{R} {dx \over 1 + x^4} .\end{align*}
What are the poles of \({1\over 1 + z^4}\) ?
Spring 2020 HW 3, SS 3.8.6 #complex/exercise/work
Show that \begin{align*} \int_{-\infty}^{\infty} \frac{d x}{\left(1+x^{2}\right)^{n+1}}=\frac{1 \cdot 3 \cdot 5 \cdots(2 n-1)}{2 \cdot 4 \cdot 6 \cdots(2 n)} \cdot \pi .\end{align*}
Quadratic over quartic #complex/exercise/work
Let \(a>0\) and calculate \begin{align*} \int_0^\infty {x^2 \over (x^2 + a^2)^2} \, dx .\end{align*}
Rational function #complex/exercise/work
Calculate \begin{align*} \int_{-\infty}^\infty {1+x^2 \over 1+x^4}\, dx .\end{align*}
Denominator polynomial #complex/exercise/work
Calculate \begin{align*} \int_0^\infty {1 \over (1+z)^2 (z+9x^2)} \, dx .\end{align*}
Rational, branch cut
Standard example #complex/exercise/work
Show that \begin{align*} \int_{{\mathbb{R}}_{\geq 0}}{x^{-s} \over x+1} = {\pi \over \sin(\pi s)} .\end{align*}
Sketch: see here.
Fall 2019.1 #complex/qual/work
Show that \begin{align*} \int_{0}^{\infty} \frac{x^{a-1}}{1+x^{n}} d x=\frac{\pi}{n \sin \frac{a \pi}{n}} \end{align*} using complex analysis, \(0<a<n\). Here \(n\) is a positive integer.
Spring 2020 HW 3.7 #complex/exercise/work
Let \(0<a<4\) and evaluate \begin{align*} \int_0^\infty \frac{x^{\alpha-1}}{1+x^3} ~dx \end{align*}
Tie’s Extra Questions: Fall 2011, Spring 2015 #complex/qual/work
Show that \begin{align*} \displaystyle \int_0^\infty \frac{x^{a-1}} {1+x^n} \,dx=\frac{\pi}{n\sin \frac{a\pi}{n}} .\end{align*} using complex analysis, \(0< a < n\). Here \(n\) is a positive integer.
Fall 2020.3, Spring 2019.2 #complex/qual/completed
Let \(a \in \mathbb{R}\) with \(0<a<3\). Evaluate \begin{align*} \int_{0}^{\infty} \frac{x^{a-1}}{1+x^{3}} d x .\end{align*}
Write \(I\) for the integral, \(\zeta_3\coloneqq e^{2\pi i\over 3}, \omega_3 \coloneqq e^{i\pi\pver 3}\). Take a indented semicircular wedge \(\Gamma\) at an angle of \(2\pi/3\), noting the pole at \(\omega_3 \coloneqq e^{i \pi \over 3}\):
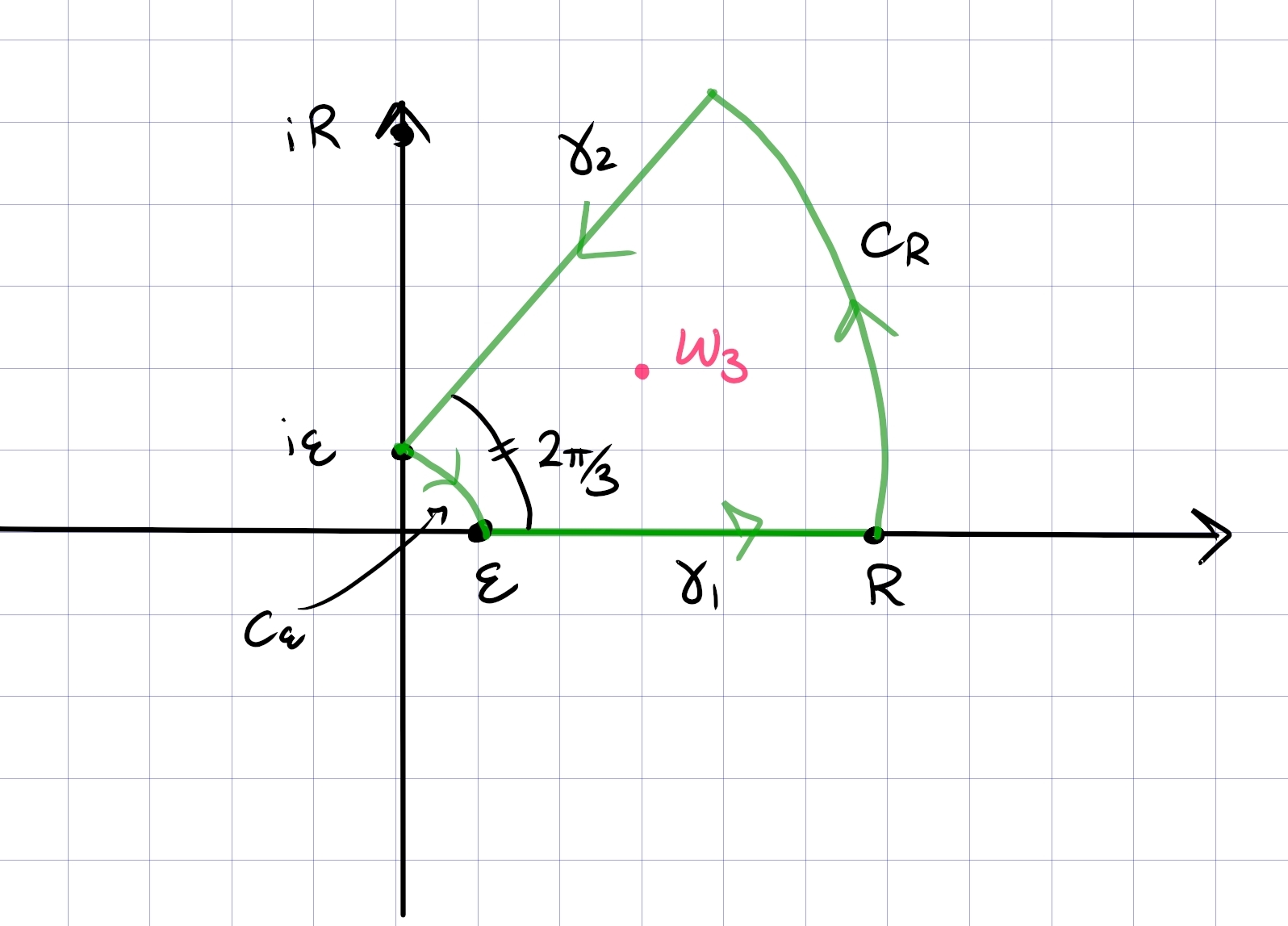
Choosing a branch cut of \(\log\) along \(\theta = -\pi/2\), so \(\arg(z) \in (-\pi/2, 3\pi/2)\), this makes \(f(z) \coloneqq z^{\alpha-1}/(1+z^3)\) meromorphic on \(\Gamma\).
By the ML estimate, the integrals along \(C_{\varepsilon}, C_R\) will vanish in the limit.
The contribution from the contour: parameterize \(\gamma_2\) as \(\left\{{\zeta_3 t{~\mathrel{\Big\vert}~}t\in [{\varepsilon}, R]}\right\}\), then \begin{align*} \int_{\gamma_2}f(z) \,dz &= \int_R^{\varepsilon}{(\zeta_3 t)^{\alpha - 1} \over 1 + (\zeta_3 t)^3} \zeta_3\,dt\\ &= \zeta_3 \zeta_3^{\alpha-1}\int_R^{\varepsilon}{t^{\alpha-1} \over 1 + t^3}\,dt\\ &\to -\zeta_3^\alpha I ,\end{align*} so the total contribution is \begin{align*} \oint_\Gamma f \to \qty{\int_{\gamma_1} + \int_{\gamma_2}}f = (1-\zeta_3^{\alpha}) I .\end{align*}
Computing the contributions from residues: \begin{align*} \mathop{\mathrm{Res}}_{z=\omega_3} f(z) &= \lim_{z\to \omega_3} {(z-\omega_3) z^{\alpha-1} \over 1+z^3} \\ &{ \overset{\scriptscriptstyle\text{LH}}{=} }\lim_{z\to\omega_3} {z^{\alpha-1} \over 3z^2} \\ &= {1\over 3} \omega_3^{\alpha-3} \\ &= -{1\over 3}\omega_3^\alpha .\end{align*}
Combining it all using the residue theorem: \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=\omega_3} f(z) &= \oint_\gamma f \\ \implies I &= {-2\pi i\over 3} {\omega_3^\alpha \over 1-\zeta_3^\alpha } \\ &= {-2\pi i\over 3} {1 \over \omega_3^{-\alpha} - \omega_3^\alpha } \\ &= {-2\pi i\over 3} {1 \over -2i\sin\qty{\pi\alpha\over 3} } \\ &= {\pi\over 3}\csc\qty{\alpha\pi\over 3} .\end{align*}
Rational Functions of \(\sin\) or \(\cos\)
Cosine in denominator #complex/exercise/work
Show \begin{align*} \int_0^{2\pi} {1\over a + \cos(\theta)} \,d\theta= {2\pi \over \sqrt{a^2-1}}, && a> 1 .\end{align*}
Sketch:
-
Set \(z=e^{i\theta}\) to get \begin{align*} \frac{2}{i} \int_{|z|=1} \frac{\mathrm{d} z}{z^{2}+2 a z+1} .\end{align*}
-
Factor into two roots \(r_1, r_2\). Use that without loss of generality, \(r_1\in {\mathbb{D}}\) and \(r_2\in {\mathbb{D}}^c\), with neither on \(S^1\) to compute the residue \(4\pi/(r_1 -r_2)\)
Spring 2020 HW 2, SS 2.6.1 #complex/exercise/work
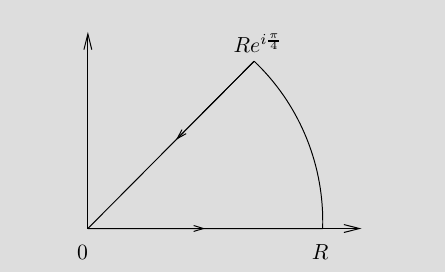
Show that \begin{align*} \int_{0}^{\infty} \sin \left(x^{2}\right) d x=\int_{0}^{\infty} \cos \left(x^{2}\right) d x=\frac{\sqrt{2 \pi}}{4} .\end{align*}
Hint: integrate \(e^{-x^2}\) over the following contour, using the fact that \(\int_{-\infty}^{\infty} e^{-x^{2}} d x=\sqrt{\pi}\):
 \
\
Spring 2020 HW 3, SS 3.8.8 #complex/exercise/work
Show that if \(a,b\in {\mathbb{R}}\) with \(a > {\left\lvert {b} \right\rvert}\), then \begin{align*} \int_{0}^{2 \pi} \frac{d \theta}{a+b \cos \theta}=\frac{2 \pi}{\sqrt{a^{2}-b^{2}}} .\end{align*}
Fresnel #complex/exercise/work
Suppose \(a>b>0\) and calculate \begin{align*} \int_0^{2\pi} {1 \over (a+b\cos(\theta))^2} \,d\theta .\end{align*}
Fresnel #complex/exercise/work
Let \(n\in {\mathbb{Z}}^{\geq 1}\) and \(0<\theta<\pi\) and show that \begin{align*} {1\over 2\pi i} \int_{{\left\lvert {z} \right\rvert} = 2} {z^n \over 1 -3z\cos(\theta) + z^2} \,dz = {\sin(n\theta) \over \sin(\theta)} .\end{align*}
Spring 2020 HW 3.10 #complex/exercise/work
For \(a> 0\), evaluate \begin{align*} \int_0^{\pi/2} \frac{d\theta}{a + \sin^2 \theta} \end{align*}
Spring 2020 HW 3, SS 3.8.7 #complex/exercise/work
Show that \begin{align*} \int_{0}^{2 \pi} \frac{d \theta}{(a+\cos \theta)^{2}}=\frac{2 \pi a}{\left(a^{2}-1\right)^{3 / 2}}, \quad \text { whenever } a>1 .\end{align*}
Rectangles
Spring 2021.2 #complex/qual/completed
Let \(\xi\in {\mathbb{R}}\), evaluate \begin{align*} \int_{\mathbb{R}}{e^{i\xi x} \over \cosh(x)} \,dx .\end{align*}
Note \(\cosh(z) \coloneqq{1\over 2}(e^z + e^{-z})\), and \begin{align*} \cosh(z) &= 0 \\ \iff e^z + e^{-z} &= 0 \\ \iff e^{-z}(e^{2z} + 1) &= 0 \\ \iff e^{2z} &= -1 \quad \text{since }{\left\lvert {e^{-z}} \right\rvert} = e^{\Re(z)} > 0 \\ \iff 2z &= (2k+1)i\pi \\ \iff z &\in \left\{{\cdots, {-3i\pi \over 2}, {-i\pi \over 2}, {i\pi \over 2}, {3i\pi \over 2}, \cdots}\right\} .\end{align*} So take the following rectangular contour enclosing the singularity \(z= i\pi/2\):
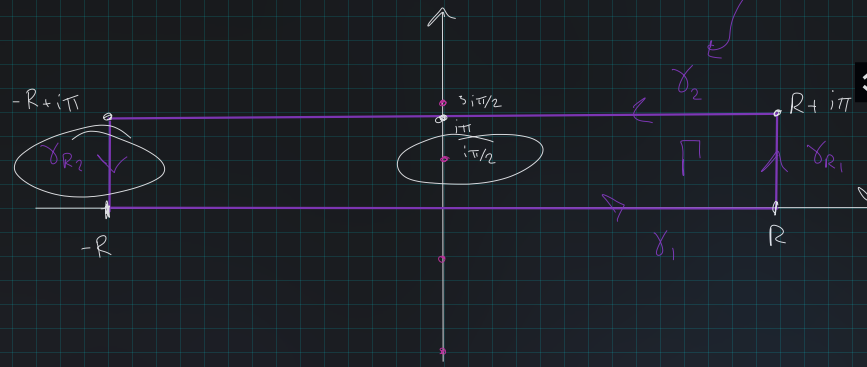
Then letting \(\Gamma\) be the entire contour and \(I\) be the desired integral, we can solve for \(I\): \begin{align*} \int_\Gamma f &= \int_{-R}^R f + \int_{\gamma_{R_1}} f + \int_{\gamma_2}f + \int_{\gamma_{R_2}} f \\ \int_\Gamma f &= I + \int_{\gamma_{R_1}} f + \int_{\gamma_2}f + \int_{\gamma_{R_2}} f \\ \\ I &= \int_{\gamma_{R_1}} f + \int_{\gamma_2}f + \int_{\gamma_{R_2}} f - \int_\Gamma f ,\end{align*} being very sloppy about the fact that we’re going to take \(R\to \infty\).
Computing the residue term \(\int_\Gamma f = 2\pi i \mathop{\mathrm{Res}}_{z=i\pi/2} f(z)\): \begin{align*} {1\over 2\ pi i } \int_\Gamma f &= \mathop{\mathrm{Res}}_{z = i\pi/2} f(z)\\ &= \mathop{\mathrm{Res}}_{z = i\pi/2} {e^{i\xi z} \over \cosh(z) } \\ &= {e^{i\xi z} \over {\frac{\partial }{\partial t}\,} \cosh(z) } \Big|_{i\pi/2}\\ &= {e^{i\xi \cdot i\pi/2} \over \sinh(i\pi/2)} \\ &= {e^{-\xi \pi/ 2} \over i} \\ \implies 2\pi i \mathop{\mathrm{Res}}_{z=i\pi/2} f(z) &= 2\pi e^{-\xi \pi/ 2} .\end{align*} using that \(2\sinh(i\pi/2) = e^{i\pi/2} - e^{-i\pi/2} = i-(-i) = 2i\).
The \(\gamma_2\) term: parameterize \(\gamma_2 = \left\{{t + i\pi {~\mathrel{\Big\vert}~}t\in [-R, R]}\right\}\), then \begin{align*} \int_{\gamma_2} f &= -\int_{-\gamma_2} f \\ &= -\int_{-R}^{R} { e^{iz} \over \cosh(t + i\pi) } \,dz, \quad z = t+i\pi, \,dz= \,dt\\ &= -\int_{-R}^{R} { e^{i\xi(t+i\pi)} \over \cosh(t + i\pi) }\,dt\\ &= -e^{-\xi \pi} \int_{-R}^R {e^{i\xi t} \over \cosh(t+i\pi)} \,dt\\ &= e^{-\xi \pi} \int_{-R}^R {e^{i\xi t} \over \cosh(t)} \,dt\\ &\coloneqq e^{-\xi \pi} I ,\end{align*} using that \(\cosh(z + i\pi) = -\cosh(z)\).
The two \(\gamma_{R_i}\) terms: the claim is that these vanish in the limit \(R\to \infty\). Parameterize \(\gamma_{R_2} = \left\{{R = i \pi t {~\mathrel{\Big\vert}~}t\in [0, 1]}\right\}\), then \begin{align*} {\left\lvert {\int_{\gamma_{R_2}} f} \right\rvert} &= {\left\lvert { \int_0^1 {e^{i\xi(R+i\pi t)} \over \cosh(R + i\pi t)} \,dt} \right\rvert} \\ &= {\left\lvert { 2e^{i\xi R} \int_0^1 {e^{-\xi \pi t } \over {e^{R+ i\pi t} + e^{-R - i\pi t}} } \,dt} \right\rvert} \\ &\leq 2 \int_0^1 {\left\lvert { {e^{-\xi \pi t } \over {e^{R+ i\pi t} + e^{-R - i\pi t}} } } \right\rvert} \,dt\\ &\leq 2 \int_0^1 {e^{-\xi \pi t } \over { {\left\lvert { e^{R+ i\pi t} } \right\rvert} - {\left\lvert { e^{-R - i\pi t} } \right\rvert} } }\,dt\\ &= 2 \int_0^1 {e^{-\xi\pi t} \over e^R - e^{-R} } \\ &= { 2\over e^R - e^{-R}} \int_0^1 e^{-\xi \pi t} \,dt\\ &= {2\over e^R - e^{-R}} \qty{-1\over \xi \pi} e^{\xi \pi t}\Big|_{t=0}^{t=1} \\ &= {2\over e^R - e^{-R}} \qty{1 - e^{-\pi \xi } \over \xi \pi} \\ &\overset{R\to\infty}\longrightarrow 0 .\end{align*}
Putting it all together: \begin{align*} (1 + e^{-\xi \pi}) I &= 2\pi e^{-\xi \pi / 2} \\ \implies I &= {2\pi e^{-\xi \pi / 2} \over 1 + e^{-\xi \pi }} \\ &= {2\pi \over e^{\xi\pi/2} (1 + e^{-\xi \pi })} \\ &= {2\pi \over e^{\xi\pi/2} + e^{-\xi\pi/2} } \\ &= {2\pi \over 2\cosh(\xi\pi/2)} \\ &= {\pi \over \cosh\qty{\xi\pi\over 2}} \\ \\ &= \pi \operatorname{sech}\qty{\xi\pi\over 2 } .\end{align*}
Spring 2020 HW 3, SS 3.8.9 #complex/exercise/work
Show that \begin{align*} \int_{0}^{1} \log (\sin \pi x) d x=-\log 2 .\end{align*}
Hint: use the following contour.

Branch Cuts
Tie’s Extra Questions: Spring 2015 #complex/exercise/work
Compute the following integrals:
- \(\displaystyle \int_0^\infty \frac{x^{a-1}}{1 + x^n} \, dx\), \(0< a < n\)
- \(\displaystyle \int_0^\infty \frac{\log x}{(1 + x^2)^2}\, dx\)
Spring 2020 HW 3, SS 3.8.10 #complex/exercise/work
Show that if \(a>0\), then \begin{align*} \int_{0}^{\infty} \frac{\log x}{x^{2}+a^{2}} d x=\frac{\pi}{2 a} \log a .\end{align*}
Hint: use the following contour.

Spring 2020.2 #complex/qual/work
Compute the following integral carefully justifying each step:
\begin{align*} \int_{0}^{\infty} \frac{\log x}{1+x^{3}} \text {. } \end{align*}
Square root in numerator #complex/exercise/work
Calculate \begin{align*} \int_0^\infty {\sqrt x \over (x+1)^2} \,dx .\end{align*}
Square root #complex/exercise/work
Calculate \begin{align*} \int_0^\infty {\sqrt x \over 1 + x^2} \, dx .\end{align*}
Trigonometric transforms
Spring 2020 HW 3, SS 3.8.4 #complex/exercise/work
Show that \begin{align*} \int_{-\infty}^{\infty} \frac{x \sin x}{x^{2}+a^{2}} d x=\pi e^{-a}, \quad \text { for all } a>0 .\end{align*}
Spring 2020 HW 2, 2.6.2 #complex/exercise/work
Show that
\begin{align*} \int_{0}^{\infty} \frac{\sin x}{x} d x=\frac{\pi}{2} .\end{align*}
Hint: use the fact that this integral eexercises \(\frac{1}{2 i} \int_{-\infty}^{\infty} \frac{e^{i x}-1}{x} d x\), and integrate around an indented semicircle.
Spring 2020 HW 3, SS 3.8.5 #complex/exercise/work
Show that if \(\xi\in {\mathbb{R}}\), then \begin{align*} \int_{-\infty}^{\infty} \frac{e^{-2 \pi i x \xi}}{\left(1+x^{2}\right)^{2}} d x=\frac{\pi}{2}(1+2 \pi|\xi|) e^{-2 \pi|\xi|} .\end{align*}
\(\sin\) in numerator #complex/exercise/work
Let \(a>0\) and calculate \begin{align*} \int_0^\infty {x\sin(x) \over x^2 + a^2} \,dx .\end{align*}
\(\sin\) in numerator #complex/exercise/work
Calculate \begin{align*} \int_0^\infty {\sin(x) \over x(x^2+1)}\, dx .\end{align*}
\(\operatorname{sinc}\) #complex/exercise/work
Calculate \begin{align*} \int_0^\infty {\sin(x) \over x}\, dx .\end{align*}
\(\cos\) in numerator #complex/exercise/work
Let \(a>0\) and calculate \begin{align*} \int_0^\infty {\cos(x) \over (x^2 + a^2)^2}\, dx .\end{align*}
\(\sin\) in numerator #complex/exercise/work
Calculate \begin{align*} \int_0^\infty {\sin^3(x) \over x^3} \, dx .\end{align*}
\(\sin\) in numerator #complex/exercise/work
Evaluate \begin{align*} \displaystyle{ \int_{0}^{\infty}\frac{x\sin x}{x^2+a^2} \, dx } .\end{align*}
Tie’s Extra Questions: Fall 2009
Evaluate \begin{align*}\displaystyle{ \int_{0}^{\infty}\frac{x\sin x}{x^2+a^2} \, dx }.\end{align*}
Cosine over quadratic #complex/exercise/completed
Show that \begin{align*} \int_0^{\infty} {\cos(x) \over x^2 + b^2}\,dx= {\pi e^{-b} \over 2b} .\end{align*}
-
Let \(I\) be the integral over \({\mathbb{R}}\). Since \(f(x)\) is even, the original integral is \({1\over 2}I\).
-
Write \(f(z) = e^{iz} / (z^2 + b^2)\). Take a semicircular contour \(\Gamma \coloneqq\gamma_1 + \gamma_2\) where \(\gamma_1\) is \([-R, R]\) on \({\mathbb{R}}\) and \(\gamma_2\) is the usual half-circle of radius \(R\).
-
Claim: \(\int_{\gamma_2} f \overset{R\to\infty}\longrightarrow 0\), so \(\int_\Gamma \to \int_{\mathbb{R}}f(z)\).
- Easy estimate, just be careful with the \(i\) in the exponent: \begin{align*} {\left\lvert {f} \right\rvert} = { {\left\lvert {e^{iz} } \right\rvert} \over {\left\lvert {z^2 + b^2} \right\rvert} } = {e^{-\Re z} \over {\left\lvert {z^2 + b^2} \right\rvert} } \leq {1\over {\left\lvert {z^2 + b^2} \right\rvert}} \overset{R\to\infty}\longrightarrow 0 .\end{align*}
-
Compute \(\int_\Gamma f\) by residues: factor \(z^2 + b^2 = (z+ib)(z-ib)\), so the contour only contains the order 1 pole \(z_0 = ib\).
-
Compute the residue: \begin{align*} \mathop{\mathrm{Res}}_{z=ib}f = \lim_{z\to ib} (z-ib) {e^{iz} \over (z+ib)(z-ib) } = { e^{iz} \over z+ib} \Big|_{z=ib} = {e^{i(ib)} \over 2ib} = {e^{-b} \over 2ib} .\end{align*}
-
So the intermediate integral is \(I\) is \(2\pi i\) times this, i.e. \(I = \pi e^{-b} / b\).
-
And the original integral is \({1\over 2}I = \pi e^{-b} \over 2b\).
Tie’s Extra Questions: Fall 2016
Compute the integral \(\displaystyle{\int_{-\infty}^{\infty} \frac{e^{-2\pi ix\xi}}{\cosh\pi x}dx}\) where \(\displaystyle{\cosh z=\frac{e^{z}+e^{-z}}{2}}\).
Tie’s Extra Questions: Fall 2015 #complex/exercise/work
Prove by justifying all steps that for all \(\xi \in {\mathbb C}\) we have \(\displaystyle e^{- \pi \xi^2} = \int_{- \infty}^\infty e^{- \pi x^2} e^{2 \pi i x \xi} dx \; .\)
Hint: You may use that fact in Example 1 on p. 42 of the textbook without proof, i.e., you may assume the above is true for real values of \(\xi\).
Multiple cosines in numerator #complex/exercise/work
Calculate \begin{align*} \int_0^\infty {\cos(x) - \cos(4x) \over x^2} \, dx .\end{align*}
Tie’s Extra Questions: Fall 2011
Evaluate \(\displaystyle{ \int_{0}^{\infty}\frac{x\sin x}{x^2+a^2} \,dx}\).
Unsorted
Spring 2020 HW 3.6 #complex/exercise/work
-
Show (without using 3.8.9 in the S&S) that \begin{align*} \int_0^{2\pi} \log{\left\lvert {1 - e^{i\theta}} \right\rvert}~d\theta = 0 \end{align*}
-
Show that this identity is equivalent to S&S 3.8.9: \begin{align*} \int_0^1 \log(\sin(\pi x)) ~dx = -\log 2 .\end{align*}
Tie’s Extra Questions: Spring 2015 #complex/exercise/work
Compute the following integrals.
-
\(\displaystyle \int_0^\infty \frac{1}{(1 + x^n)^2} \, dx\), \(n \geq 1\)
-
\(\displaystyle \int_0^\infty \frac{\cos x}{(x^2 + a^2)^2} \, dx\), \(a \in \mathbb R\)
-
\(\displaystyle \int_0^\pi \frac{1}{a + \sin \theta} \, d \theta\), \(a>1\)
-
\(\displaystyle \int_0^{\frac{\pi}{2}} \frac{d \theta}{a+ \sin ^2 \theta},\) \(a >0\).
-
\(\displaystyle \int_{|z|=2} \frac{1}{(z^{5} -1) (z-3)} \, dz\)
-
\(\displaystyle \int_{- \infty}^{\infty} \frac{\sin \pi a}{\cosh \pi x + \cos \pi a} e^{- i x \xi} \, d x\), \(0< a <1\), \(\xi \in \mathbb R\)
-
\(\displaystyle \int_{|z| = 1} \cot^2 z \, dz\).
Conceptual
Spring 2020 HW 3, SS 3.8.1 #complex/exercise/work
Use the following formula to show that the complex zeros of \(\sin(\pi z)\) are exactly the integers, and they are each of order 1: \begin{align*} \sin \pi z=\frac{e^{i \pi z}-e^{-i \pi z}}{2 i} .\end{align*}
Calculate the residue of \({1\over \sin(\pi z)}\) at \(z=n\in {\mathbb{Z}}\).
Zeros using residue theorem #complex/exercise/work
Suppose that \(f\) is an analytic function in the region \(D\) which contains the point \(a\). Let \begin{align*}F(z)= z-a-qf(z),\quad \text{where}\quad q \ \text{is a complex parameter}.\end{align*}
-
Let \(K\subset D\) be a circle with the center at point \(a\) and also we assume that \(f(z)\not =0\) for \(z\in K\). Prove that the function \(F\) has one and only one zero \(z=w\) on the closed disc \(\mkern 1.5mu\overline{\mkern-1.5muK\mkern-1.5mu}\mkern 1.5mu\) whose boundary is the circle \(K\) if \begin{align*} \displaystyle{ |q|<\min_{z\in K} \frac{|z-a|}{|f(z)|}.} .\end{align*}
-
Let \(G(z)\) be an analytic function on the disk \(\mkern 1.5mu\overline{\mkern-1.5muK\mkern-1.5mu}\mkern 1.5mu\). Apply the residue theorem to prove that \begin{align*} \displaystyle{ \frac{G(w)}{F'(w)}=\frac{1}{2\pi i}\int_K \frac{G(z)}{F(z)} dz,} \end{align*} where \(w\) is the zero from (1).
Tie’s Extra Questions: Fall 2009 #complex/exercise/work
Suppose that \(f\) is an analytic function in the region \(D\) which contains the point \(a\). Let \begin{align*}F(z)= z-a-qf(z),\quad \text{where}~ q \ \text{is a complex parameter}.\end{align*}
-
Let \(K\subset D\) be a circle with the center at point \(a\) and also we assume that \(f(z)\not =0\) for \(z\in K\). Prove that the function \(F\) has one and only one zero \(z=w\) on the closed disc \(\mkern 1.5mu\overline{\mkern-1.5muK\mkern-1.5mu}\mkern 1.5mu\) whose boundary is the circle \(K\) if \(\displaystyle{ |q|<\min_{z\in K} \frac{|z-a|}{|f(z)|}.}\)\
-
Let \(G(z)\) be an analytic function on the disk \(\mkern 1.5mu\overline{\mkern-1.5muK\mkern-1.5mu}\mkern 1.5mu\). Apply the residue theorem to prove that \(\displaystyle{ \frac{G(w)}{F'(w)}=\frac{1}{2\pi i}\int_K \frac{G(z)}{F(z)} dz,}\) where \(w\) is the zero from (1).\
-
If \(z\in K\), prove that the function \(\displaystyle{\frac{1}{F(z)}}\) can be represented as a convergent series with respect to \(q\): \(\displaystyle{ \frac{1}{F(z)}=\sum_{n=0}^{\infty} \frac{(qf(z))^n}{(z-a)^{n+1}}.}\)
Tie’s Extra Questions: Spring 2015 #complex/exercise/completed
Let \(\displaystyle{\psi_{\alpha}(z)=\frac{\alpha-z}{1-\mkern 1.5mu\overline{\mkern-1.5mu\alpha\mkern-1.5mu}\mkern 1.5muz}}\) with \(|\alpha|<1\) and \(\mathbb D = \{z:\ |z|<1\}\). Prove that
-
\begin{align*} \displaystyle{\frac{1}{\pi}\iint_{{\mathbb D}} |\psi'_{\alpha}|^2 dx dy =1} .\end{align*}
-
\begin{align*} \displaystyle{\frac{1}{\pi}\iint_{{\mathbb D}} |\psi'_{\alpha}| dx dy =\frac{1-|\alpha|^2}{|\alpha|^2} \log \frac{1}{1-|\alpha|^2}} .\end{align*}
Part 1: S&S claim this can be done without a calculation – maybe \({\left\lvert {\psi_a'(z)} \right\rvert}^2\) is constant on a circle of radius \(r\)…?
Part 2: \begin{align*} {1\over \pi} \iint_{\mathbb{D}}{\left\lvert {\psi_a'(z)} \right\rvert} \,dz &= {1\over \pi} \iint_{\mathbb{D}}{\left\lvert {1- {\left\lvert {a} \right\rvert}^2 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu z)^2 } \right\rvert} \,dz\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 \int_0^{2\pi} {1 \over {\left\lvert { 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu re^{it} } \right\rvert}^2 } r\,dt\,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 \int_0^{2\pi} {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu re^{it} )(1 - a re^{-it}) } r\,dt\,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 \oint_{{{\partial}}{\mathbb{D}}} {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu rz )(1 - a r \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu) } {r\over iz} \,dz\,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 \oint_{{{\partial}}{\mathbb{D}}} {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu rz )(1 - a r z^{-1}) } {r\over iz} \,dz\,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 {r\over i} \cdot \oint_{{{\partial}}{\mathbb{D}}} {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu rz )(z - a r) } \,dz\,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 {r\over i} \cdot 2\pi i \mathop{\mathrm{Res}}_{z=ar} {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu rz )(z - a r) } \,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 {r\over i} \cdot 2\pi i {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu rz ) }\Big|_{z=ar} \,dr\\ &= {2\pi \qty{ 1- {\left\lvert {a} \right\rvert}^2} \over \pi} \int_0^1 {r \over 1- {\left\lvert {a} \right\rvert}^2r^2 } \,dr\\ &= {1-{\left\lvert {a} \right\rvert}^2 \over {\left\lvert {a} \right\rvert}^2} \log\qty{1 \over 1 - {\left\lvert {a} \right\rvert}^2 } .\end{align*}