Geometry
The sum of the interior angles of an \(n{\hbox{-}}\)gon is \((n-2)\pi\), where each angle is \(\frac{n-2}{n}\pi\).
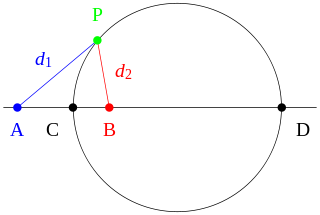
- Circle: \(x^2 + y^2 = r^2\), or equivalently \({\left\lvert {z-a} \right\rvert}=c\) or \({\left\lvert {z-a} \right\rvert} = c{\left\lvert {z-b} \right\rvert}\), the locus of points whose distances to two fixed points \(A, B\) is a constant ratio not equal to 1, so \(d_1/d_2 = c\):
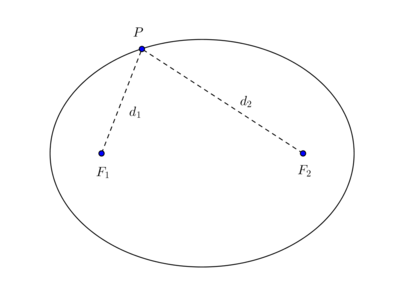
- Ellipse: \(\qty{\frac x a}^2 + \qty{\frac y b}^2 = 1\), or equivalently \({\left\lvert {z-a} \right\rvert} + {\left\lvert {z-b} \right\rvert} = c\) Equivalently, the locus of points whose sums of distances to two fixed points points \(A, B\) is a constant, so \(d_1 + d_2 = c\):
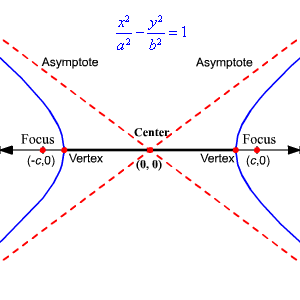
- Hyperbola: \(\qty{\frac x a}^2 - \qty{\frac y b}^2 = 1\) or equivalently \({\left\lvert {z-a} \right\rvert} - {\left\lvert {z-b} \right\rvert} = c\):
- Rectangular Hyperbola: \(xy = \frac{c^2}{2}\).
- Parabola: \(-4ax + y^2 = 0\).
Another way to distinguish: write \(f(x, y) = Ax^2 + Bxy + Cy^2 + \cdots\), then consider the discriminant \(\Delta = B^2 - 4AC\):
-
\(\Delta < 0 \iff\) ellipse
- \(\Delta < 0\) and \(A=C, B=0 \iff\) circle
- \(\Delta = 0 \iff\) parabola
- \(\Delta > 0 \iff\) hyperbola
Some useful parametric equations:
- For ellipses \(\qty{x\over a}^2 + \qty{y\over b}^2 = 1\), take \({\left[ {a\cos(t), b\sin(t)} \right]}\):

-
In complex form: \(\gamma(t) = ae^{it} + be^{-it}\).
-
What the parameters mean:
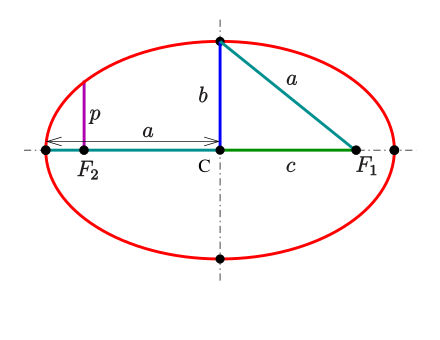
- The foci are at \((\pm c, 0)\) where \(c\coloneqq\sqrt{a^2-b^2}\) assuming \(a\geq b\).
- The vertices are \((\pm a, 0)\) and \((0, \pm b)\).
-
For off-center circles \((x-h)^2 + (y-k)^2 = r^2\), use \({\left[ {r\cos(t) + h, r\sin(t) + k} \right]}\).
- In complex form: \(\gamma(t) = z_0 + re^{it}\) where \(z_0\coloneqq h + ik\).
-
Setting \(u\coloneqq\tan(t/2)\), \begin{align*} \cos(t) = {1-u^2\over 1+u^2} && \sin(t) = {2u\over 1+u^2} .\end{align*}
- Rational parameterization of an ellipse: \begin{align*} {\left[ {a {1-u^2\over 1+u^2} , b {2u\over 1+u^2}} \right]} = a {1-u^2\over 1+u^2} +ib{2u\over 1+u^2} .\end{align*}
- Rational parameterization of a circle: just take \(a=b=R\), \begin{align*} {\left[ {R {1-u^2\over 1+u^2} , R {2u\over 1+u^2}} \right]} = R {1-u^2\over 1+u^2} +iR{2u\over 1+u^2} .\end{align*}
-
Lines: \(\overline{a}z + a\overline{z} + c = 0\).
Algebra
Some useful numerology that comes up when trying to estimate when poles fall within a disc:
- \(\sqrt{2} \approx 1.4142\)
- \(1/\sqrt{2} \approx 0.707\)
- \(\sqrt{3} \approx 1.732\)
- \(1/\sqrt{3} \approx 0.577\)
- \(e\approx 2.718\)
- \(\pi \approx 3.14159\)
\begin{align*} x^2 + bx + c = 0 \iff x^2 + bx {\color{red\, + \qty{b\over 2}^2 - \qty{b\over 2}^2 } + c = 0 \\ \iff \qty{x+ \qty{b\over 2}^2}^2 + \qty{c - \qty{b\over 2}^2} = 0 .\end{align*}
More generally: \begin{align*} ax^2 + bx + c = 0 \iff x^2 + {b\over a}x + {c\over a} = 0 \\ \iff x^2 + {b\over a}x + {\color{red} \qty{b/a \over 2}^2 - \qty{b/a \over 2}^2} + c = 0 \\ \iff (x + {b\over 2a})^2 + \qty{c - \qty{b\over 2a}^2} = 0 .\end{align*}
So given \(ax^2+bx+c=0\), you can always write it as \(a(x+d)^2 + e\) where \(d\coloneqq b/2a\) and \(e\coloneqq c - (b/2a)^2\).