Define \(\qty{n}^{ (k) }\) to be the rising factorial \begin{align*} \qty{n}^{ (k) } = n(n+1)(n+2) \cdots (n+(k-1)) = k! {n+k-1\choose k} ,\end{align*} which has exactly \(k\) terms. Some useful identities: \begin{align*} \qty{n}^{ (k) } &= {(n+k-1)! \over (k-1)!} = {\Gamma(n+k) \over \Gamma(n)} \\ { \qty{n}^{ (k) } \over k!} &= {n+k-1 \choose k} .\end{align*}

Similarly define the falling factorial \begin{align*} \qty{n}_{ (k) } = n(n-1)(n-2)\cdots(n-(k-1)) = k!{n\choose k} ,\end{align*} which again has \(k\) terms. \begin{align*} \qty{n}_{ (k) } &= {n! \over (n-k)!} = {\Gamma(n+1) \over \Gamma(n - (k-1))}\\ { \qty{n}_{ (k) } \over k!} &= {n\choose k} .\end{align*}

Where this comes up most often: \begin{align*} \qty{{\frac{\partial }{\partial z}\,}}^k z^n = \qty{n}_{ (k) } \, z^{n-k} .\end{align*}

Extend the binomial coefficients to negative numbers in the following way: \begin{align*} {-n \choose k} &\coloneqq(-n)(-(n+1))\cdots (-(n + (k-1))) \cdot {1\over k!} = (-1)^k {n+k-1 \choose k} .\end{align*} Then \begin{align*} (x+y)^n = \sum_{k\geq 0} {n\choose k} x^{k}y^{n-k} .\end{align*}

\begin{align*} \sum_{k=1}^{n} k &=\frac{n(n+1)}{2} \\ \sum_{k=1}^{n} k^{2} &=\frac{n(n+1)(2 n+1)}{6} \\ \sum_{k=1}^{n} k^{3} &=\frac{n^{2}(n+1)^{2}}{4} \\ \sum_{0\leq k \leq N} z^k &= {1 - z^{N+1} \over 1-z} \\ {1\over 1-z} &= \sum_{k\geq 0} z^k \\ e^z &= \sum_{k\geq 0} {z^k \over k!} \\ \sin(z) &= \sum_{\substack{ k \geq 1 \\ \text{odd} }} (-1)^{k+1 \over 2} {z^k \over k!} \\ &= z - {1\over 3!}z^3 + {1\over 5!}z^5 + \cdots \\ \\ \cos(z) &= \sum_{\substack{ k \geq 0 \\ \text{even}} } (-1)^{k\over 2} {z^k \over k!} \\ &= 1 - {1\over 2!}z^2 + {1\over 4!}z^4 + \cdots \\ \\ \cosh(z) &= \sum_{k\geq 0} { z^{2k} \over (2k)! } \\ &= 1 + {1\over 2!}z^2 + {1\over 4!}z^4 + \cdots \\ \\ \sinh(z) &= \sum_{k\geq 0} { z^{2k+1} \over (2k+1)! } \\ &= z + {1\over 3!}z^3 + {1\over 5!}z^5 + \cdots \\ \\ \log(1-z) &= -1\cdot \sum_{k \geq 1} {z^k\over k} \quad {\left\lvert {z} \right\rvert} < 1 \\ \\ \qty{{\frac{\partial }{\partial z}\,}}^k \sum_{n=0}^\infty c_n z^n &= \sum_{n=k}^\infty (n)_k \, c_n z^{n-k} \\ &= \sum_{n=k}^\infty n(n-1)\cdots(n-k+1) c_n z^{n-k} \\ (1+z)^{1/2} &= \sum_{k\geq 0} {1/2 \choose k}z^k,\qquad {\left\lvert {z} \right\rvert} < 1 \\ &= 1 + (1/2)z + {(1/2)(-1/2) \over 2!}z^2 + {(1/2)(-1/2)(-3/2) \over 3!}z^3 + \cdots \\ &= 1 + {1\over 2}z - {1\over 8}z^2 + {1\over 16}z^3 - \cdots \\ (1+z)^{\alpha} &= \sum_{k\geq 0} {\alpha \choose k}z^k,\qquad {\left\lvert {z} \right\rvert} < 1 \\ {1\over 1+z^n} &= \sum_{k\geq 0} {n+k-1 \choose k} (-z)^k, \qquad {\left\lvert {z} \right\rvert} < 1 \end{align*}

Some other classes of series to remember: \begin{align*} \sum_{k=1}^{n} k &= \frac{n(n+1)}{2} \\ \sum_{k=1}^{n} k(k+1) &= \frac{n(n+1)(n+2)}{3} \\ \sum_{k=1}^{n} k(k+1)(k+2) &= \frac{n(n+1)(n+2)(n+3)}{4} \\ \vdots \quad & \vdots \\ \sum_{k=1}^{n} k^{(p)} &= \frac{n^{(p+1)}}{p+1} && k^{(p)}\coloneqq k(k+1)(k+2) \cdots (k+p-1) .\end{align*} How to remember: compare to the integral \begin{align*} \int_{x=0}^{x=n} x^p \,dx= { n^{p+1} \over p+1} .\end{align*}

Remembering that \(\sum_{1\leq k \leq n} k = n(n+1)/2\): realize as counting a triangle, flip to count an entire rectangle of size \(n\times (n+1)\) and take half:

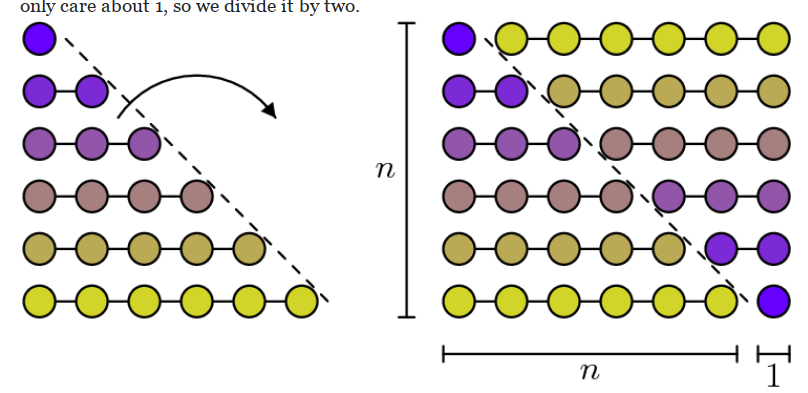
Write \(k^2 = k(k+1) - k\) to get \begin{align*} \sum k^2 = \sum k(k+1) - \sum k = {n(n+1/2)(n+2/2) \over 3} .\end{align*} Similarly \(\sum k^3 = (\sum k )^2\).

For summing the odds, \(\sum_{k\geq 1} (2k-1)\):

For denominators: \begin{align*} \sum_{k=1}^{n} \frac{1}{k(k+1)}=\frac{1}{1}-\frac{1}{n+1} \\ \sum_{k=1}^{n} \frac{2}{k(k+1)(k+2)}=\frac{1}{1 \cdot 2}-\frac{1}{(n+1)(n+2)} \\ \sum_{k=1}^{n} \frac{p}{k^{(p+1)}}=\frac{1}{1^{(p)}}-\frac{1}{(n+1)^{(p)}} ,\end{align*} where \(1^{(p)} \coloneqq p!\). How to remember the last one: \begin{align*} \int_{x=1}^{x=n+1}{p\over x^{p+1}}\,dx= {1\over 1^p} - {1\over (n+1)^p} .\end{align*}

\begin{align*} \sqrt{z} &= \sqrt{z_0 + z - z_0} \\ &= \sqrt{z_0 \qty{ 1 + {z-z_0 \over z} }} \\ &= \sqrt{z_0} \sqrt{1+u},\quad u\coloneqq{z-z_0 \over z} \\ \implies \sqrt{z} &= \sqrt{z_0} \sum_{k\geq 0} {1/2 \choose k} \qty{z- z_0 \over z}^k .\end{align*}

The product of two sequences is given by the Cauchy product \begin{align*} \sum a_kz^k \cdot \sum b_k z^k = \sum c_k z^k,\quad c_k \coloneqq\sum_{j\leq k} a_k b_{k-j} .\end{align*}

Using the general ring theory fact that \(A(z) \coloneqq\sum_{k\geq 0} a_k z^k \in R[[z]]\) is invertible iff \(a_0\) is invertible in \(R\), power series over fields can always be inverted. There is a formula: writing \(B(z) \coloneqq\sum_{k\geq 0 } b_k z^k \coloneqq 1/A(z) \in {\mathbf{C}}[[z]]\), the coefficients can be inductively computed as \begin{align*} b_0 &= a_0^{-1}\\ b_n &= -a_0^{-1}\sum_{1\leq i \leq n} a_i b_{n-i} \\ &= -a_0^{-1}\sum_{0\leq i \leq n-1} a_{n-i}b_i \\ &= -{1\over a_0}\qty{a_nb_0 + a_{n-1}b_1 + \cdots + a_1 b_{n-1} } .\end{align*}

Supposing \(A(z) \coloneqq 1 + a_1 z + a_2z^2 + \cdots\), a direct expansion gives \begin{align*} {1\over A(z)} &= {1\over 1 + \displaystyle\sum_{k\geq 1} a_k z^k }\\ &= 1 - \qty{\sum_{k\geq 1} a_k z^k} \ + \qty{\sum_{k\geq 1} a_k z^k}^2 \ - \qty{\sum_{k\geq 1} a_k z^k}^3 \ + \cdots \\ &= 1 - (A(z) - 1) + (A(z) - 1)^2 - (A(z) - 1)^3 + \cdots ,\end{align*} where to compute the \(z^m\) term you only need to consider the first \(m+1\) summands in this expansion.

Purely formally, we have \begin{align*} {1\over A(z)} = {1 \over 1- (1-A(z))} = \sum_{k\geq 0} (1-A(z))^k z^k .\end{align*}

Polynomial long division basically works for formal power series, and with practice it’s fast enough to just do in your head. Recall the Euclidean algorithm, e.g. for \({z^3+1 \over z+1}\): \begin{align*} z^3 + 1 &= (z+1)(z^2) + (-z^2 + 1) \\ \ -z^2 + 1 &= (z+1)(-z) + (z+1) \\ (z+1) &= (z+1)(1) + 0 \\ \implies {z^3 + 1\over z+1} &= z^2 - z + 1 .\end{align*} This goes by increasing powers, but one can also go by decreasing powers: \begin{align*} 1+z^3 &= (1+z)(1) + (-z+z^3) \\ \ -z+z^3 &= (1+z)(-z) + (z^2 + z^3) \\ z^2 +z^3 &= (1+z)(z^2) + 0 \\ \implies {z^3 + 1\over z+1}&= 1 - z + z^2 ,\end{align*} which is useful for generating the first few low order terms of a series expansion.