There are formulas: \begin{align*} &e^{a i \omega}+e^{b i \omega} &=2 \cos \left(\frac{a-b}{2} \omega\right) e^{\frac{a+b}{2} i \omega} \\ e^{a i \omega}-e^{b i \omega} &=2 i \sin \left(\frac{a-b}{2} \omega\right) e^{\frac{a+b}{2} i \omega} .\end{align*} Why this is useful: you can reduce a sum of two exponentials to a complex scalar times a real trig function, e.g. when computing a residue to get a real number. Why this is true: for the right choice of \(\ell\), \begin{align*} e^{aiw} + e^{biw} = e^{\ell iw} \qty{ e^{(l-a)iw} + e^{(\ell - b)iw} } = e^{\ell i w} \qty{ e^{kiw} + e^{-kiw}} = e^{\ell i w}\cdot 2\cos(kw) .\end{align*} To make this hold, choose
- \(\ell \coloneqq{a+b\over 2}\)
- Then \(\ell - a = {b-a \over 2} \coloneqq k\)
- \(\ell -b = {a-b\over 2} = -k\)
An example: \begin{align*} e^{-i\pi \over 2}+ e^{-3i\pi \over 2} &\coloneqq e^{-iw} + e^{-3iw} \\ &= e^{-2iw} \qty{e^{iw} + e^{-iw}}\\ &= e^{-2iw}\cdot 2\cos(w) \\ &= e^{-2i\cdot {\pi \over 2}}\cdot 2\cos\qty{\pi \over 2} \\ &= -i\cdot 0 = 0 .\end{align*}
\begin{align*} z + \overline{z} &= 2\Re(z) && z - \overline{z} = 2i\Im(z) \\ z\overline{z} &= {\left\lvert {z} \right\rvert}^2 && \operatorname{Arg}(z/w) = \operatorname{Arg}(z) - \operatorname{Arg}(w) \\ \Re(z) &= { z + \overline{z} \over 2} && \Im(z) = {z - \overline{z} \over 2i} \\ {1\over i} &= -i = i^3 && {1\over i^3} = i .\end{align*}
Exponential forms of cosine and sine, where it’s sometimes useful to set \(w\coloneqq e^{iz}\): \begin{align*} \cos(z) &= \frac 1 2 \qty{e^{iz} + e^{-iz}} = {1\over 2}(w+ w^{-1})\\ \sin(z) &= \frac{1}{2i}\qty{e^{iz} - e^{-iz}} = {1\over 2i}(w-w^{-1}) .\end{align*}
Exponential forms of hyperbolic cosine and sin: \begin{align*} \cosh(z) &= \cos(iz) = {1\over 2}\qty{e^z + e^{-z}} \\ \sinh(z) &= -i \sin(iz) = {1\over 2}\qty{e^z - e^{-z}} .\end{align*}
Some other useful facts about the hyperbolic exponentials:
- They are periodic with period \(2\pi i\).
- \({\frac{\partial }{\partial z}\,}\cosh(z) = \sinh(z)\) and \({\frac{\partial }{\partial z}\,}\sinh(z) = \cosh(z)\).
- \(\sinh\) is odd and \(\cosh\) is even.
- \(\cosh(z + i\pi) = -\cosh(z)\) and \(\sinh(z + i\pi) = -\sinh(z)\).
- \(\cosh\) has zeros at \(\left\{{i\pi\qty{2k+1\over 2}}\right\} = \left\{{i \qty{\pi/2 + k\pi}}\right\}\), i.e. \(\cdots, -\pi/2, \pi/2, 3\pi/2,\cdots\), the half-integers.
- \(\sinh\) has zeros at \(\left\{{i\pi k}\right\}\), i.e. the integers.
- \(\sinh(z)\) has a particularly nice formula for derivatives: \begin{align*} f(z) &\coloneqq\cosh(z) \implies f^{(n)}(z) = {e^z + (-1)^n e^{-z}\over 2} \\ f(z) &\coloneqq\sinh(z) \implies f^{(n)}(z) = {e^z - (-1)^{n} e^{-z}\over 2} .\end{align*}
Some computations that come up frequently: \begin{align*} {\left\lvert {z \pm w} \right\rvert}^2 &= {\left\lvert {z} \right\rvert}^2 + {\left\lvert {w} \right\rvert}^z + 2\Re(\overline{w}z) \\ (a+bi)(c+di) &= (ac - bd) + (ad + bc) \\ {1\over {\left\lvert {a+b} \right\rvert}} &\leq {1 \over {{\left\lvert {a} \right\rvert} - {\left\lvert {b} \right\rvert}}} && {\left\lvert {e^{z}} \right\rvert} = e^{\Re(z)}, \quad \arg(e^z) = \Im(z) .\end{align*}
The inversion \(z\to 1/z\) is easiest to understand in polar coordinates, \(Re^{i\theta}\mapsto {1\over R}e^{-i\theta}\):
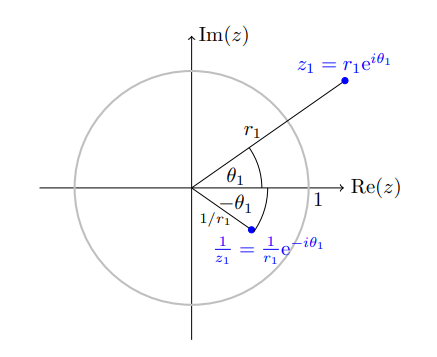
Exercises
Solve \(z^4=i\).
First find a principal root: \(z^4=i = e^{i\pi\over 2} \implies z_0 = e^{i\pi \over 8}\). Now all of the roots are \(\left\{{z_k = z_0 \zeta_4^k {~\mathrel{\Big\vert}~}k=0,1,2,3}\right\}\) where \(\zeta_4=e^{2\pi i \over 4} = e^{i\pi \over 2}\), so
- \(z_0 = e^{i\pi \over 8} e^{0i\pi \over 4} = e^{i\pi \over 8}\) corresponding to \({1\over 8} + {0\over 4}\),
- \(z_1 = e^{i\pi \over 8} e^{1i\pi \over 4} = e^{3i\pi \over 8}\) corresponding to \({1\over 8} + {1\over 4} = {3\over 8}\),
- \(z_2 = e^{i\pi \over 8} e^{2i\pi \over 4} = e^{5i\pi \over 8}\) corresponding to \({1\over 8} + {2\over 4} = {5\over 8}\),
- \(z_3 = e^{i\pi \over 8} e^{3i\pi \over 4} = e^{7i\pi \over 8}\) corresponding to \({1\over 8} + {3\over 4} = {7\over 8}\).
Find \(\Re\qty{z+2\over z-1}\).
\begin{align*} {z+2\over z-1}\cdot{\overline{z-1} \over \overline{z-1}} &= {(z+2)\overline{z-1} \over {\left\lvert {z-1} \right\rvert}^2} \\ &= {((z-1) + 3)\overline{z-1} \over {\left\lvert {z-1} \right\rvert}^2} \\ &= {{\left\lvert {z-1} \right\rvert}^2 + 3\overline{z} -3 \over {\left\lvert {z-1} \right\rvert}^2} \\ &= {(x-1)^2 + y^2 + 3(x-iy) - 3 \over (x-1)^2 + y^2} \\ &= {(x-1)^2 + 3x - 3 + y^2\over (x-1)^2 + y^2} + i{-3y\over (x-1)^2 + y^2} \\ &= {(x-1)(x+2) + y^2\over (x-1)^2 + y^2} + i{-3y\over (x-1)^2 + y^2} .\end{align*}
Find an identity for \(\cos(4\theta)\) in terms of \(\sin(\theta)\) and \(\cos(\theta)\).
Write \(x=\cos(\theta), y= \sin(\theta)\), so \(e^{i\theta} = x+iy\). Then \begin{align*} \cos(4\theta) + i\sin(4\theta) &= e^{4i\theta } \\ &= (x+iy)^4 \\ &= \sum_{0\leq k \leq 4} {4\choose k} x^k (iy)^{4-k} \\ &= x^4 + 4ix^3y - 6x^2y^2 - 4ixy^3 + y^4 \\ &= (x^4 - 6x^2y^2 + y^4) + i(4x^3y - 4xy^3) .\end{align*} So \begin{align*} \cos(4\theta) &= \cos^4(\theta) - 6\cos^2(\theta)\sin^2(\theta) + \sin^4(\theta)\\ \sin(4\theta) &= \cos^3(\theta)\sin(\theta) + \cos(\theta)\sin^3(\theta) .\end{align*}
Show that \({\left\lvert {e^z} \right\rvert} = e^{\Re(z)}\).
Write \(z=x+iy\), so \(\Re(z) = x\). Then \begin{align*} {\left\lvert {e^z} \right\rvert} = {\left\lvert {e^{x+iy}} \right\rvert} = {\left\lvert {e^x} \right\rvert}{\left\lvert {e^{iy}} \right\rvert} = {\left\lvert {e^x} \right\rvert} ,\end{align*} using that \(e^x>0\) for all \(x\in {\mathbf{R}}\).
Show that \({z-1\over z+1}\) is purely imaginary \(\iff z\in S^1\).
Hint: \(z\) is real iff \(\overline{z} = z\) and purely imaginary iff \(\overline{z} = -z\).
\begin{align*} {z-1\over z+1} = -\qty{\overline{z} - 1 \over \overline{z} + 1} \iff (z-1)(1+z) = (1-\overline{z})(1+\overline{z}) \iff2-2{\left\lvert {z} \right\rvert}^2 = 0 \iff {\left\lvert {z} \right\rvert}^2 = 1 .\end{align*}