Any \(z\neq 0\) can be written in the form \begin{align*} z = {\left\lvert {z} \right\rvert} e^{i\arg(z)} ,\end{align*} where \(\arg(z)\) is the multivalued function \(\arg(z) = \operatorname{Arg}(z) + 2\pi n\) where \(\operatorname{Arg}(z)\in (-\pi, \pi]\) is the principal value of the argument. Note that it’s not necessarily true that if \(z=x+iy\) that \(\operatorname{Arg}(z) = \arctan\qty{y\over x}\), because \(\arctan\) is also multivalued. There is a formula based on which quadrant \(z\) is in:

Note that \(\operatorname{Arg}(0)\) is undefined, so that \(\operatorname{Arg}(z)\) makes sense on \({\mathbf{C}}\setminus(-\infty, 0]\), where \((\infty, 0]\) is a branch cut. Any choice of interval \((\theta_0, \theta_0 + 2\pi]\) yields a different branch cut.
Since \(\log(z)\) and \(z^\alpha\) are defined in terms of \(\operatorname{Arg}\), this is where most branching issues come from!
There are two ways to define \(z^{1\over 2}\):
- \(f_1(z) = \sqrt{{\left\lvert {z} \right\rvert}} e^{i{ \operatorname{Arg}(z) \over 2} } = \sqrt{r}\cos\qty{\theta\over 2} + i\sqrt{r} \sin\qty{\theta\over 2}\).
- \(f_2(z) = \sqrt{{\left\lvert {z} \right\rvert}} e^{i{ \operatorname{Arg}(z) + 2\pi \over 2} } = \sqrt{r}\cos\qty{\theta + 2\pi \over 2} + i\sqrt{r} \sin\qty{\theta + 2\pi \over 2}\).
Note that \begin{align*} f_2(z) = \sqrt{r}e^{i{\operatorname{Arg}(z) + 2\pi \over 2} } = \sqrt{r} e^{i{\operatorname{Arg}(z) \over 2}}e^{i\pi} = -\sqrt{r}e^{i{\operatorname{Arg}(z) \over 2}} = -f_1(z) .\end{align*}
Let \(z_0 = r_0e^{i\pi} \in (-\infty, 0) \subseteq {\mathbf{R}}\), and show that \(z^{1\over 2}\) is not continuous along \((-\infty, 0)\) by computing \begin{align*} \lim_{z\in \gamma_1} f_1(z) &= i\sqrt{r_0} \\ \lim_{z\in \gamma_2} f_1(z) &= -i\sqrt{r_0} ,\end{align*}
where
- \(\gamma_1 = \left\{{r_0 e^{it} {~\mathrel{\Big\vert}~}t\in (0, \pi) }\right\}\),
- \(\gamma_2 = \left\{{r_0 e^{-it} {~\mathrel{\Big\vert}~}t\in (\pi, 0) }\right\}\)
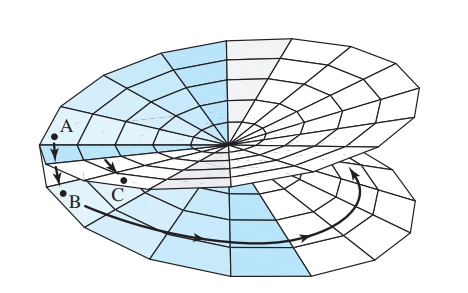
\begin{align*} \lim _{(r, \theta) \rightarrow\left(r_{0}, \pi\right)} f_{1}\left(r e^{i \theta}\right) &=\lim _{(r, \theta) \rightarrow\left(r_{0}, \pi\right)} r^{\frac{1}{2}}\left(\cos \frac{\theta}{2}+i \sin \frac{\theta}{2}\right)=i r_{0}^{\frac{1}{2}}, \quad \text { and } \\ \lim _{(r, \theta) \rightarrow\left(r_{0},-\pi\right)} f_{1}\left(r e^{i \theta}\right) &=\lim _{(r, \theta) \rightarrow\left(r_{0},-\pi\right)} r^{\frac{1}{2}}\left(\cos \frac{\theta}{2}+i \sin \frac{\theta}{2}\right)=-i r_{0}^{\frac{1}{2}} . .\end{align*}
Define \begin{align*} \log(z) \coloneqq\ln\qty{{\left\lvert {z} \right\rvert}} + i\operatorname{Arg}(z) ,\end{align*} where \(\operatorname{Arg}(z)\) is the principal argument in \((-\pi, \pi]\). Note that this is sometimes written \begin{align*} \log(z) \coloneqq\ln\qty{{\left\lvert {r} \right\rvert}} + i\theta .\end{align*}
\begin{align*} \log(1+i) = \ln\qty{\sqrt 2} + \qty{{\pi\over 4} + 2k\pi}i .\end{align*} Note that this assigns an infinite number of complex numbers to \(1+i\), all on the line \(\Re(z) = \ln\qty{\sqrt 2}\) with imaginary parts differing by multiples of \(2\pi\).
The principal branch of \(\operatorname{Log}\) is defined so that \(\operatorname{Log}(1) = 0\), and can be written as \begin{align*} \operatorname{Log}(z) = \int_\gamma {1\over \xi} \,d\xi \end{align*} where \(\gamma\) is any piecewise smooth path connecting 1 to \(z\).
Define \begin{align*} z^\alpha \coloneqq e^{\alpha \log(z)} ,\end{align*} where some branch of \(\log\) (usually the principal branch) is implicitly chosen.
If \(\Omega\) is a connected domain with \(f\in {\mathcal{O}}^{\times}(\Omega)\) an invertible regular function with \begin{align*} \int_\gamma {f'\over f} = 0 \end{align*} for all \(\gamma \subseteq \Omega\), then
-
There exists a holomorphic \(g:\Omega\to {\mathbf{C}}\) such that \(g = \log(f)\) and \(e^g = f\).
-
\(g' = {f'\over f}\), yielding an explicit formula \begin{align*} g(z) = g(z_0) + \int_{z_0}^z {f'(\xi) \over \xi}\,d\xi .\end{align*}
\(\operatorname{Log}(f(z))\) has branch points at the zeros of \(f\).
Common trick: \begin{align*} f^{1/n} = e^{{1\over n} \log(f)} ,\end{align*} taking (say) a principal branch of \(\log\) given by \({\mathbf{C}}\setminus(-\infty, 0] \times 0\).
Suppose \(\Omega\) is a simply-connected region such that \(1\in \Omega, 0\not\in\Omega\). Then there exists a branch of \(F(z) \coloneqq\operatorname{Log}(z)\) such that
- \(F\) is holomorphic on \(\Omega\),
- \(e^{F(z)} = z\) for all \(z\in \Omega\)
- \(F(x) = \log(x)\) for \(x\in {\mathbf{R}}\) in a neighborhood of \(1\).
Show that
- \(\log(zw)\neq \log(z)\log(w)\)
- \(\log(\exp(z))\neq z\)
Counterexamples:
-
Take \(z=\zeta_4^3\) and \(w=\zeta_4^2\), noting that \(\operatorname{Arg}(z) = {3\pi \over 4}\) and \(\operatorname{Arg}(w) = {\pi \over 2}\) Then \(zw = e^{5\pi \over 4}\) but \(\operatorname{Arg}(zw) = {-3\pi \over 4}\) because we are forced to use the domain \((-\pi, \pi]\).
-
Showing that \(\log(\exp(z))\) is a countably infinite set in \({\mathbf{C}}\): \begin{align*} \log(\exp(z)) &= \log(\exp(x+iy)) \\ &= \ln\qty{e^x} + (y+2k\pi)i \\ &= (x+iy) + 2k\pi i \\ &= z + 2k\pi .\end{align*}
\begin{align*} \operatorname{Log}(zw) &\neq \operatorname{Log}(z) + \operatorname{Log}(w) \\ \operatorname{Log}(e^z) &\neq z .\end{align*}
For counterexamples, take \(z=\zeta_4^3=\exp(3\pi i / 4\) and \(w=\zeta_4^2 = \exp(\pi i/2)\). Then \(zw= \exp(-3 \pi i /4)\), using that the domain of \(\operatorname{Arg}\) is \((-\pi, \pi]\).
Note the problem: for \(z\coloneqq x+i0 \in {\mathbf{R}}^{\leq 0}\), just above the axis consider \(z_+ \coloneqq x + i{\varepsilon}\) and \(z_- \coloneqq x-i{\varepsilon}\). Then
- \(\log(z_+) = \log{\left\lvert {x} \right\rvert} + i\pi\), and
- \(\log(z_-) = \log{\left\lvert {x} \right\rvert} - i\pi\).
So \(\log\) can’t even be made continuous if one crosses the branch. The issue is the branch point or branch singularity at \(z=0\).
If \(f\) is holomorphic and nonvanishing on a simply-connected region \(\Omega\), then there exists a holomorphic \(G\) on \(\Omega\) such that
\begin{align*} f(z) = e^{G(z)} .\end{align*}
The complex exponential is \(2\pi i\) periodic, and invertible on any horizontal strip of the form \begin{align*} S_\alpha \coloneqq\left\{{z\in {\mathbf{C}}{~\mathrel{\Big\vert}~}\Im(z) \in [\alpha, \alpha+2\pi] }\right\} .\end{align*}
Generally choose branch cuts that are slits between branch points to prevent monodromy around those points. One can find branch points for \(\log(f(z))\) by noting that \(\log\) should be a primitive of \({\frac{\partial }{\partial z}\,}\log(f(z))\).
-
\(\log(z^2-1)\) has branch points at \(z=\pm 1,\ infty\). To see \(\infty\) is a branch point: by differentiating, the log should be a primitive of \({2z\over z^2-1}\). Taking a large curve, each term contributes \(2\pi i\) with the same sign, so the value jumps.
So a cut like \((-\infty, +1]\) works, and an explicit formula may be obtained by taking:
- \(\log(z+1) + \log(z-1) = (r_1 + i\theta_1) + (r_2 + i\theta_2)\).
-
\(\log\qty{z+1\over z-1}\): needs to be a primitive for \({1\over z+1} + {1\over z-1}\), so \(\pm 1\) are branch points. \(z=\infty\) is not a branch point, because integrating over a large curve yields \(+2\pi i - 2\pi i = 0\), so no monodromy.
- So a cut like \([-1, 1]\) works, with a formula \(\log(z+1) - \log(z-1) = (r_1 + i\theta_1) - (r_2 + i\theta_2)\).
Prove that if \(D\) is a simply connected domain and \(f(z)\) is holomorphic and nonzero on \(D\), then \(f(z)=e^{g(z)}\), where \(g(z)\) is holomorphic on \(D\).
