See reference
Suppose \(f\) is holomorphic on \(\Omega\), then for any \(z_0 \in \Omega\) and any open disc \(\overline{D_R(z_0)}\) such that \(\gamma \coloneqq{{\partial}}\overline{D_R(z_0)} \subseteq \Omega\), \begin{align*} f(z_0) = {1 \over 2\pi i} \int_{\gamma} {f(\xi) \over \xi-z_0}\ \,d\xi \end{align*} and \begin{align*} f^{(n)}(z_0) = {n! \over 2\pi i} \int_{\gamma} {f(\xi) \over (\xi - z_0)^{n+1}} \,d\xi .\end{align*} As a consequence, if \(f(z) \sum_{k\geq 0} c_k (z-z_0)^k\), \begin{align*} c_k = {f^{(n)}(z_0) \over n!} = {1\over 2\pi i} \int_\gamma { f(\xi) \over (\xi - z_0)^{n+1} } \,d\xi .\end{align*}



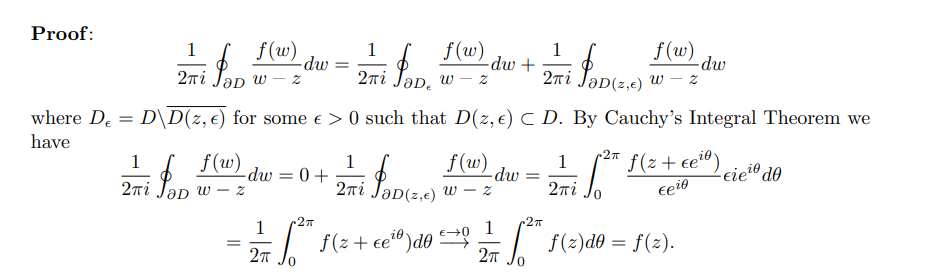
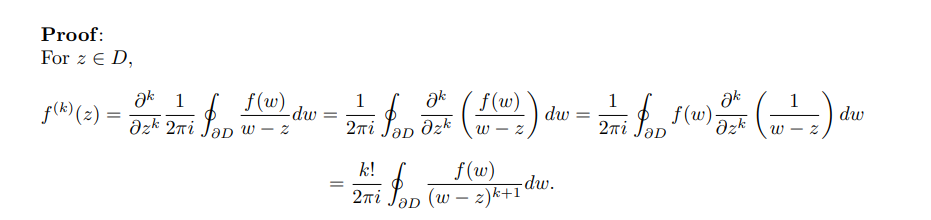
Exercises
Compute \begin{align*} \int_{{{\partial}}{\mathbb{D}}} {e^z\over z^2}\,dz .\end{align*}
By Cauchy’s formula, \begin{align*} \int {f(z) \over (z-0)^2}\,dz= 2\pi i f^{(1)}(0) = 2\pi i .\end{align*}
Without using the residue formula, compute \begin{align*} \int_{\mathbf{R}}f(x) \,dx&& f(x) \coloneqq{1\over x^4 + 16} .\end{align*}
Use a semicircular contour, noting the poles are at \(\pm \sqrt 2 \pm i\sqrt 2\). Write
- \(f_1(z) \coloneqq(\sqrt 2 + i\sqrt 2)f(z)\)
- \(f_2(z) \coloneqq(-\sqrt 2 + i\sqrt 2) f(z)\).
Break the curve up into two integrals \(I_1, I_2\) enclosing the poles, by Cauchy one gets
- For the loop around the right pole: \(I_1 = 2\pi i f_1(\sqrt 2 + i\sqrt 2) = {\pi \sqrt{2}(1-i) \over 32}\)
- For the loop around the left pole: \(I_2 = 2\pi i f_2(\sqrt 2 - i\sqrt 2) = {\pi \sqrt 2(1+i) \over 32}\).
Now show that \(\int_{C_R}\) vanishes: parameterize as \(\gamma(t) = Re^{it}\) and use the reverse triangle inequality: \begin{align*} {\left\lvert { \int_{C_R} f} \right\rvert} \leq \int_0^\pi {1\over R^4 - 16} = {\pi R \over R^4-16}\to 0 .\end{align*}
Suppose \(f\) is holomorphic on \(\Omega\), a simply connected region, and suppose \(\gamma \subseteq \Omega\). Using the Cauchy integral formula, show that \begin{align*} \int_\gamma {f'(z) \over z-a}\,dz= \int_\gamma {f(z) \over (z-a)^2 }\,dz .\end{align*} Also prove this when \(\Omega\) is not simply connected.
Use the integral formula directly: \begin{align*} \int_\gamma {f'(z) \over z-a}\,dz= 2\pi i f'(a) .\end{align*}
On the other hand, use Cauchy’s formula for derivatives: \begin{align*} \int_\gamma {f(z) \over (z-a)^2}\,dz= 2\pi i f^{(1)}(a) ,\end{align*} and these values are equal.
If \(\Omega\) is not simply connected, note that by the quotient rule \begin{align*} {\frac{\partial }{\partial z}\,} {f(z) \over z-a} = {f'(z)\over z-a} - {f(z) \over (z-a)^2} .\end{align*}
Thus \begin{align*} \int_\gamma {f'(z) \over z-a} - \int_\gamma {f(z) \over (z-a)^2}\,dz &= \int_\gamma \qty{ {f'(z) \over z-a} - {f(z) \over (z-a)^2} }\,dz\\ &= \int_\gamma {\frac{\partial }{\partial z}\,} {f(z) \over z-a} \,dz\\ &= G(\gamma(1)) - G(\gamma(0)) \\ &= G(p) - G(p) \\ &= 0 ,\end{align*} where \(G(z) \coloneqq{f(z) \over z-a}\) is a primitive for the integrand by definition.
Evaluate the following integrals using Cauchy’s integral formula:
\begin{align*} \int_{S^1} {\cos(z) \over z} \,dz&\\ \int_{S^1} {\sin(z) \over z}\,dz&\\ \int_{{\left\lvert {z} \right\rvert} = 2} {z^2\over z-1} \,dz&\\ \int_{S^1} {e^z \over z^2} \,dz&\\ \int_{{\left\lvert {z} \right\rvert} = 2} {z^2 - 1 \over z^2 + 1}\,dz&\\ \int_{{\left\lvert {z} \right\rvert} = 2} {1\over z^2 + z + 1}\,dz& .\end{align*}
\begin{align*} \int_{S^1} {\cos(z) \over z} \,dz &= 2\pi i \cos(0) \\ &= 2\pi i \\ \\ \int_{S^1} {\sin(z) \over z}\,dz &= 2\pi i \sin(0) \\ &= 0 \\ \\ \int_{{\left\lvert {z} \right\rvert} = 2} {z^2\over z-1} \,dz &= 2\pi i z^2\Big|_{z=1} \\ &= 2\pi i \\ \\ \int_{S^1} {e^z \over z^2} \,dz &= 2\pi i {\frac{\partial }{\partial z}\,} e^z\Big|_{z=0} \\ &= 2\pi i \\ \\ \int_{{\left\lvert {z} \right\rvert} = 2} {z^2 - 1 \over z^2 + 1}\,dz &= \int_{{\mathbb{D}}+ i} {(z^2 -1)/(z+i) \over z-i}\,dz+ \int_{{\mathbb{D}}- i} {(z^2-1)/(z-i) \over z+i} \,dz\\ &= 2\pi i \qty{z^2-1\over z+i}\Big|_{z=i} + 2\pi i \qty{z^2-1 \over z-i}\Big|_{z=-i} \\ &= 2\pi i \qty{-2\over 2i} + 2\pi i \qty{-2\over -2i} \\ &= 0 \\ \\ \int_{{\left\lvert {z} \right\rvert} = 2} {1\over z^2 + z + 1}\,dz &= \int {1\over (z-\zeta_3) (z- \overline{\zeta_3} )} \,dz\\ &= \int_{{\mathbb{D}}+ \overline{ \zeta_3} } {1/(z-\zeta_3) \over (z- \overline{\zeta_3} )} \,dz+ \int_{{\mathbb{D}}+ {\zeta_3} } {1/(z- \overline{ \zeta_3} ) \over (z- {\zeta_3} )} \,dz\\ &= 2\pi i \qty{1\over z-\zeta_3}\Big|_{z=\overline{\zeta_3}} + 2\pi i \qty{1\over z-\overline{\zeta_3}}\Big|_{z=\zeta_3} \\ &= 2\pi i \qty{ {1\over \overline{\zeta_3} - \zeta_3 } + {1\over \zeta_3 - \overline{\zeta_3}} }\\ &= 2\pi i \qty{ {1\over \overline{\zeta_3} - \zeta_3 } - {1\over \overline{\zeta_3} - {\zeta_3}} } \\ &= 0 ,\end{align*} where for the last we note that \(\zeta_3 = e^{2\pi i \over 3} = -1 + i\sqrt 3\) and \(\zeta_3 \overline{\zeta_3} = 2\Re(\zeta_3) = 2\cdot {1\over 2} = 1\), yielding the factorization of the denominator.