If \(f\) is entire and bounded, \(f\) is constant.
- Since \(f\) is bounded, \(f(z) \leq M\) uniformly on \({\mathbf{C}}\).
- Apply Cauchy’s estimate for the 1st derivative: \begin{align*} {\left\lvert {f'(z)} \right\rvert} \leq { 1! {\left\lVert {f} \right\rVert}_{C_R} \over R } \leq {M \over R}\overset{R\to\infty}\longrightarrow 0 ,\end{align*} so \(f'(z) = 0\) for all \(z\).
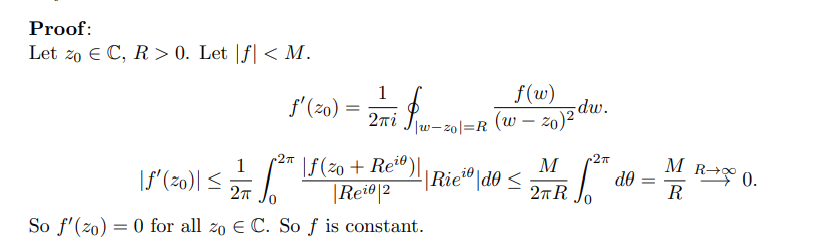
Suppose \(f\) is entire and bounded. Under an affine change of variables in the domain and range, \(f(0) = 0\) and \({\left\lvert {f(z)} \right\rvert} \leq 1\), the claim is that \(f\equiv 0\). The function \(g(z) \coloneqq f(Rz)\) satisfies the Schwarz lemma, so \({\left\lvert {f(Rz)} \right\rvert} \leq {\left\lvert {z} \right\rvert} \implies {\left\lvert {f(w)} \right\rvert} \leq {\left\lvert {w} \right\rvert}/R\overset{R\to\infty}\longrightarrow 0\).
Exercises
Show that an entire doubly periodic function is constant.
Show that if \(f, g\) are entire with \({\left\lvert {f(z)} \right\rvert}\leq {\left\lvert {g(z)} \right\rvert}\), then \(f(z) = cg(z)\) for some constant \(c\).
Write \(h \coloneqq f/g\), so \(h\) is meromorphic with \({\left\lvert {h} \right\rvert} \leq 1\). Moreover, \(h\) can only have singularities where \(g (z_k) = 0\), but is bounded by 1 in punctured neighborhoods about any such \(z_k\). So any such singularities are removable, and \(h\) extends over the singularities by Riemann’s removable singularity theorem to give an entire function. Now \(h\) is bounded and entire, thus constant, so \(c = h = f/g \implies f=cg\).
Show that if \({\left\lvert {f(z)/z^n} \right\rvert}\) is bounded for \({\left\lvert {z} \right\rvert}\geq R\), then \(f\) is a polynomial of degree at most \(n\). What happens if this bound holds on all of \({\mathbf{C}}\)?
Use that \(f\) is entire to Laurent expand at \(z=0\) to get \(f(z) = \sum_{k\geq 0}c_k z^k\) everywhere. Claim: \(c_{n+k} = 0\) for all \(k\geq n+1\) By the formula for Taylor coefficients, it suffices to show \(f^{(n+k)}(0) = 0\) for all \(k\geq n+1\). Apply the Cauchy estimate on a curve of radius \(R\gg 1\): \begin{align*} {\left\lvert { f^{n+k} (0)} \right\rvert} &\leq {(n+k)! \over 2\pi} \int_{{\left\lvert {z} \right\rvert} = R} {\left\lvert {f(\xi) \over \xi^{n+k+1}} \right\rvert}\,d\xi\\ &\leq {(n+k)! \over 2\pi} \int_{{\left\lvert {z} \right\rvert} = R} {\left\lvert {M \over \xi^n \xi^{k+1}} \right\rvert}\,d\xi\\ &= {(n+k)! \over 2\pi} \int_{{\left\lvert {z} \right\rvert} = R} {\left\lvert {M \over R ^{k+1}} \right\rvert}\,d\xi\\ &= {(n+k)! \over 2\pi} {M\over R^{k+1}} \cdot 2\pi R \\ &= { \mathsf{O}}(1/R) \to 0 .\end{align*}
If this holds on all of \({\mathbf{C}}\), then \(h(z) \coloneqq f(z)/z^n\) is constant and thus \(f(z) = cz^n\).
Find all entire functions \(f\) satisfying \begin{align*} {\left\lvert {f(z)} \right\rvert} \geq {\left\lvert {z} \right\rvert} + 1 &&\forall z\in {\mathbf{C}} .\end{align*}
The inequality implies \(f\) has no zeros, so \(g(z) \coloneqq 1/f(z)\) is entire. Moreover it is bounded on \({\mathbf{C}}\), since \begin{align*} {\left\lvert {g(z)} \right\rvert} \leq {1\over {\left\lvert {z} \right\rvert} + 1} \leq 1 ,\end{align*} so \(g\equiv c\) is constant by Liouville. This means \(f\equiv c\) is constant, but \(\lim_{z\to \infty}g(z) = 0\) forces \(c=\infty\), so there are no such entire functions.
Let \(f\) be entire and suppose that for \({\left\lvert {z} \right\rvert} \geq M\), \begin{align*} {\left\lvert {f} \right\rvert} \leq A + B{\left\lvert {z} \right\rvert}^k \end{align*} for some constants \(A, B\) and \(k\). Show that \(f\) is a polynomial of degree at most \(k\).
Apply a Cauchy estimate over a contour of radius \(R> M\) to obtain \begin{align*} {\left\lvert {f^{(n)}(0)} \right\rvert} \leq n!{A+B R^k \over R^n} \ll 1/R^{n-k} ,\end{align*} and if \(n>k\) then this goes to zero in \(R\) and \(c_n = 0\) for all \(n>k\).
Suppose \({\left\lvert {f(z)} \right\rvert}\leq {\left\lvert {g(z)} \right\rvert}\) for all \(z\). What conclusion can you draw?
Write \(h(z) \coloneqq f(z)/g(z)\), then \({\left\lvert {f} \right\rvert}\leq 1\) is bounded. Provided the zeros of \(g\) do not have a limit point, the singularities of \(h\) are isolated and thus removable. By Riemann’s removable singularity theorem, \(h\) extends to an entire function. By continuity, \({\left\lvert {h(z)} \right\rvert}\leq 1\) on \({\mathbf{C}}\) and is thus bounded. By Liouville \(h\) is constant, making \(f = cg\) for some \(c\).
Suppose \(f\) is entire and for every \(z\), \begin{align*} {\left\lvert {f(z)} \right\rvert}\leq {\left\lvert {\sin(z)} \right\rvert} .\end{align*} Characterize all possibilities for \(f\).
Write \(g(z) \coloneqq f(z) / \sin(z)\), which is meromorphic with singularities at the zeros of \(\sin(z)\) and bounded by 1. By boundedness, these singularities are removable, so \(g\) extends to a bounded entire and thus constant function. So \(f(z) = c\sin(z)\) where \({\left\lvert {c} \right\rvert} \leq 1\).
Let \(f\) be entire with \(\operatorname{im}(f) \cap{\mathbb{D}}_r(z_0)\) empty. Show \(f\) must be constant without using the Casorati-Weierstrass or Picard theorems.
Write \(g(z) \coloneqq f(z) - z_0\), so \({\left\lvert {g(z)} \right\rvert} \geq r\). Now \({\left\lvert {1/g(z)} \right\rvert} \leq 1/r\) for all \(z\), so \(1/g\) is bounded. Moreover it is entire since \(f(z) \neq z_0\) for any \(z\), and so \(1/g = c\) is constant. Now unwind to get \(f(z) = z_0 + {1\over c}\), which is also constant.
Show that if \(f\) is entire and \({\left\lvert {f(z)} \right\rvert} > 1\) for all \(z\), then \(f\) is constant.
The inequality forces \(f\neq 0\) anywhere, so \(1/f\) is entire and bounded by 1. By Liouville, \(1/f\) is constant, and thus so is \(f\).
Let \(f\) be an entire function. Assume that for some \(k \in \mathbb{N}\), and sufficiently large \(|z|\), we have that \(|f(z)| \leq A+B|z|^{k}\). Prove that \(f\) is a polynomal of degree at most \(k\).
By induction on \(k\), suppose that if \(f\) is degree \(k-1\) with \({\left\lvert {f} \right\rvert} \leq A + B{\left\lvert {z} \right\rvert}^{k-1}\) outside of a large enough disc. Let \(f\) be degree \(k\), and consider \begin{align*} g(z) \coloneqq \begin{cases} f'(0) & z=0 \\ {f(z) - f(0) \over z-0} & z=0. \end{cases} .\end{align*} Then outside of a large enough disc, \begin{align*} {\left\lvert {g} \right\rvert} \sim {A+B{\left\lvert {z} \right\rvert}^k \over {\left\lvert {z} \right\rvert}} \leq_{\sim} B{\left\lvert {z} \right\rvert}^{k-1} ,\end{align*} and moreover by the MMP \(g\) is bounded inside such a disc. So \(g\) is a polynomial of degree at most \(k-1\) by hypothesis, making \(f\) degree at most \(k\).
Show that if \(f:{\mathbf{C}}\to {\mathbf{C}}\) is nonconstant and entire then \(f({\mathbf{C}})\) is dense in \({\mathbf{C}}\).
Supposing not, then there is some \({\mathbb{D}}_R(w) \cap f({\mathbf{C}})\) empty. Then \(g(z) \coloneqq{1\over f(z) - w}\) is bounded in this disc and reflects to an entire bounded function, thus constant. Then if \(g\) is constant, \(f\) is constant.