The logarithmic derivative is defined as \begin{align*} { {\partial}^{\scriptsize \log} }f \coloneqq{f' \over f} .\end{align*}
It converts all poles and zeros of meromorphic \(f\) into simple poles of \({ {\partial}^{\scriptsize \log} }f\). If \(z_0\) is a root of \(f\) of multiplicity \(m\), write \(f(z) = (z-z_0)^m g(z)\) with \(g\) holomorphic and nonzero near \(z_0\). Then take log derivatives: \begin{align*} { {\partial}^{\scriptsize \log} }f(z) &= { {\partial}^{\scriptsize \log} }(z-z_0)^m g(z) \\ &= { {\partial}^{\scriptsize \log} }(z-z_0)^m + { {\partial}^{\scriptsize \log} }g(z) \\ &= {m\over (z-z_0)} + {g'(z) \over g(z)} .\end{align*}
Then if \(g\) is holomorphic and nonzero away from \(z_0\), so is \(g'/g\). So the only contribution to \(\mathop{\mathrm{Res}}_{z=z_0} { {\partial}^{\scriptsize \log} }f\) is \(m\).
Note that the logarithmic derivative picks up the \(p{\hbox{-}}\)adic valuation for \(\left\langle{x-p}\right\rangle \in {\mathbf{C}}[x]\) a point: \begin{align*} d \qty{ \log(f) } = {f'\over f}\,dz\implies \mathop{\mathrm{Res}}_{z=p}(d \log(f) ) = v_p(f) .\end{align*}
For \(\gamma \subseteq \Omega\) a closed curve not passing through a point \(z_0\), the winding number of \(\gamma\) about \(z_0\) (or the index) is defined as \begin{align*} \mathop{\mathrm{Index}}_{z=z_0}(\gamma) \coloneqq{1\over 2\pi i} \int_\gamma {1\over \xi -z_0}\,d\xi .\end{align*}
For \(f\) meromorphic in \(\Omega\) with multisets of zeros \(Z_f \coloneqq\left\{{ z_j }\right\}\) and poles \(P_f\coloneqq\left\{{ p_k }\right\}\) (so repeated with multiplicity) for \(\gamma \coloneqq{{\partial}}\Omega\) not intersecting any of the zeros/poles,
\begin{align*} {1\over 2\pi i} \int_\gamma { {\partial}^{\scriptsize \log} }f(z) \,dz \coloneqq{1\over 2\pi i} \int_\gamma {f'(z) \over f(z)} \,dz= &= {\sharp}Z_f - {\sharp}P_f ,\end{align*} where \({\sharp}Z_f\) and \({\sharp}P_f\) are the number of zeros and poles respectively, counted with multiplicity. If \(f\) is holomorphic, then \begin{align*} {1\over 2\pi i} \oint_{{{\partial}}\Omega} {f'(z) \over f(z)}\,dz &= \sum_{z_k\in f^{-1}(0) \cap\Omega} \mathrm{mult}(f, z_k) \\ {1\over 2\pi i} \oint_{{{\partial}}\Omega} {zf'(z) \over f(z)}\,dz &= \sum_{z_k\in f^{-1}(0) \cap\Omega} f(z_k) \mathrm{mult}(f, z_k) \\ .\end{align*}
-
If \(z_0\) is a zero of \(f\) of order \(m\), write \(f(z) = (z-z_0)^m g(z)\) with \(g(z)\) holomorphic and nonzero on some neighborhood of \(z_0\).
-
Compute \begin{align*} { {\partial}^{\scriptsize \log} }f(z) &= \frac{m\left(z-z_{0}\right)^{m-1} g(z)+\left(z-z_{0}\right)^{m} g^{\prime}(z)}{\left(z-z_{0}\right)^{m} g(z)} \\ &= {m \over z-z_0} + { {\partial}^{\scriptsize \log} }g(z) ,\end{align*} so \(z_0\) is a simple pole of \({ {\partial}^{\scriptsize \log} }f\) and \(\operatorname{res}_{z=z_0} { {\partial}^{\scriptsize \log} }f = m\).
-
If \(z_0\) is a pole of \(f\) of order \(m\), write \(f(z) = (z-z_0)^{-m} g(z)\), then \begin{align*} { {\partial}^{\scriptsize \log} }f = {-m \over z-z_0} + { {\partial}^{\scriptsize \log} }g ,\end{align*} so \(z_0\) is a simple pole and \(\mathop{\mathrm{Res}}_{z=z_0} {\partial}_{\log f} = -m\).
-
Now apply the residue theorem, and group residues according to sign: \begin{align*} {1\over 2\pi i } \int_{\gamma} {\partial}_{\log }f(z) \,dz &= \sum_{z_i \in P_{{ {\partial}^{\scriptsize \log} }f}} \mathop{\mathrm{Res}}_{z=z_i} { {\partial}^{\scriptsize \log} }f(z)\\ &= \sum_{z_k \in Z_f} \mathop{\mathrm{Res}}_{z=z_k} f(z) - \sum_{z_j \in P_f} \mathop{\mathrm{Res}}_{z=z_j} f(z) .\end{align*}
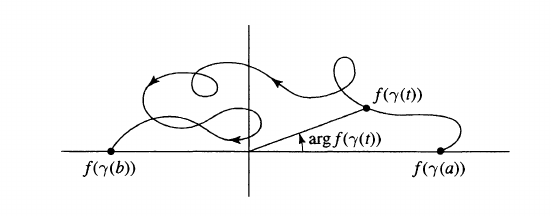
With the same setup as above, \begin{align*} {1\over 2\pi i} \int_\gamma { {\partial}^{\scriptsize \log} }f(z) \,dz &= \mathop{\mathrm{Index}}_{w=0}(f\circ \gamma)(w) .\end{align*}
Make the change of variables \(w = f(z)\), then \(z=\gamma(t) \mapsto w = (f\circ \gamma)(t)\) and \(\,dw= f'(z) \,dz\), so \begin{align*} {1\over 2\pi i }\int_{\gamma} { {\partial}^{\scriptsize \log} }f(z) \,dz = {1\over 2\pi i} \int_{f\circ \gamma} {1\over w} \,dw\coloneqq\mathop{\mathrm{Index}}_{w=0} (f\circ \gamma)(w) .\end{align*}
Let \(f(z) = z^2 + z = z(z+1)\).
- \(\gamma_1 \coloneqq\left\{{{\left\lvert {z} \right\rvert} = 2}\right\}\) contains 2 zeros and 0 poles, so \(f\circ \gamma\) winds twice around zero counterclockwise.
- \(\gamma_2 \coloneqq\left\{{{\left\lvert {z} \right\rvert} = {1\over 2}}\right\}\) contains 1 zero and 0 poles, so \(f\circ \gamma\) winds once.
You can track the change in argument by just breaking a curve up into sub-curves and evaluating a branch of the \(\arg\) function at the endpoints. For example, in this picture, the change in argument is \(\pi\) no matter what the curve does in \({\mathbb{H}}\):
The integral function \begin{align*} F(w) \coloneqq{1\over 2\pi i} \oint_{{{\partial}}\Omega} {f'(z) \over f(z) - w} \,dw \end{align*} counts the number of solutions to \(f(z) = w\) in \(\Omega\), since it’s of the form \(\int_\gamma { {\partial}^{\scriptsize \log} }g_w(z)\,dz\) for \(g_w(z) \coloneqq f(z) - w\). This is continuous provided \(f(z) \neq w\) on \({{\partial}}\Omega\) and is \({\mathbf{Z}}{\hbox{-}}\)valued, thus constant on connected components.
Also useful: zeros of \(f\) with multiplicity \(m\geq 2\) are zeros of \(f'\). This also holds for \(f(z) -a\).
Exercises
Show that \({ {\partial}^{\scriptsize \log} }(fg) = { {\partial}^{\scriptsize \log} }f + { {\partial}^{\scriptsize \log} }g\), i.e. \begin{align*} { (fg)' \over fg} = {f'\over f} + {g' \over g} .\end{align*}
\begin{align*} {(fg)' \over fg} = { f'g + fg' \over fg} = {f'g \over fg} + {fg' \over fg} = {f'\over f} + {g' \over g} .\end{align*}
Show that if \(z_0\) is a zero of \(f'\) of order \(n-1\), then \(f\) is \(n\)-to-one in a neighborhood of \(z_0\).
Wlog, assume \(z_0 = 0\). We want to show that there exists discs \(U = {\mathbb{D}}_r(0)\) and \(W = {\mathbb{D}}_R(0)\) such that the fiber of \(f:U\to W\) has exactly \(n\) distinct points. Since \(0\) is a zero of order \(n\), expand \(f\) as \(\sum_{k\geq n} c_k z^k = z^n\sum_{k\geq 0} c_{k+n}z^k\). By dividing coefficients through, we may assume \(c_n = 1\), so \begin{align*} f(z) = z^n + \qty{ c_{n+1} z^{n+1} + c_{n+2}z^{n+2} + \cdots} = z^n + z^{n+1} \sum_{k\geq 0} c_{k+n+1}z^k \coloneqq z^n + g(z) .\end{align*}
By Rouché, \(f(z)\) and \(z^n\) have the same number of zeros in a small disc \({\mathbb{D}}_\rho(0)\).
Write \(m(z) = \sum_{k\geq 0}c_{k+n}z^k\) and \(M(z) = z^n\); then if \({\left\lvert {m(z)} \right\rvert} < {\left\lvert {M(z)} \right\rvert}\) for any circle \({\left\lvert {z} \right\rvert} = \rho\) with \(\rho< 1\) then \(M\) and \(m+M = f\) will have the same number of zeros (\(n\) with multiplicity).
Bounding \(m\), the tail of the Laurent series of \(f\): by Cauchy’s integral formula, on a disc of radius \(R\), \begin{align*} c_k = {f^{(n)}(z_0) \over n!} = {1\over 2\pi i} \oint_{{\left\lvert {\xi} \right\rvert} = R} { f(\xi) \over (\xi - z_0)^{n+1} } \,d\xi ,\end{align*} so \begin{align*} {\left\lvert {c_k} \right\rvert} \leq \max_{{\left\lvert {\xi} \right\rvert} = R}{\left\lvert {f(\xi)} \right\rvert} R^{-k} \coloneqq{M_R \over R^{k}} .\end{align*}
We can now estimate \(g\): \begin{align*} {\left\lvert {g(z)} \right\rvert} &= {\left\lvert {z^n \sum_{k\geq 0} c_{k+n+1} z^k} \right\rvert} \\ &\leq {\left\lvert {z} \right\rvert}^n \sum_{k\geq 0} {\left\lvert { c_{k+n+1}} \right\rvert} {\left\lvert {z} \right\rvert}^k \\ &\leq \sum_{k\geq 0} {M_R \over R^{k+n+1}} \rho^k \\ &= {\left\lvert {z} \right\rvert}^n {M_R \over R^{n+1}} \sum_{k\geq 0} \qty{\rho\over R}^k \\ &= {\left\lvert {z} \right\rvert}^n {M_R \over R^{n+1}} \qty{1\over 1- {\rho \over R}} \\ &= {\left\lvert {z} \right\rvert}^n {M_R \over R^{n+1}} {R\over R-\rho} \\ &= {\left\lvert {z} \right\rvert}^n \qty{ {M_R\over R^n( R-\rho)} } \\ &\coloneqq{\left\lvert {z} \right\rvert}^n C_{R, \rho} ,\end{align*} and \(R, \rho\) can be chosen such that \(C_{R, \rho} < 1\).
Thus on \({\left\lvert {z} \right\rvert} = \rho\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {g(z) } \right\rvert} \leq C_{R, \rho} {\left\lvert {z} \right\rvert} < {\left\lvert {z} \right\rvert} = {\left\lvert {M(z)} \right\rvert} .\end{align*}
So the fiber above \(z=0\) is of size \(n\), the claim is that this is also true in a neighborhood of zero. The above estimate also shows that for \(0 < {\left\lvert {z} \right\rvert}\leq \rho\), \({\left\lvert {g(z)} \right\rvert} \leq {\left\lvert {z^n} \right\rvert}\), and so \begin{align*} {\left\lvert {g(z)} \right\rvert} = {\left\lvert {g(z) - z^n + z^n} \right\rvert} \geq {\left\lvert { {\left\lvert {g(z) - z^n} \right\rvert} - {\left\lvert {z^n} \right\rvert} } \right\rvert} > 0 ,\end{align*} so \(g\) is nonzero on \({\mathbb{D}}_\rho(0)\setminus\left\{{0}\right\}\). For the zero-counting function \begin{align*} F(w) \coloneqq{1\over 2\pi i} \oint_{{\left\lvert {\xi} \right\rvert} = \rho'} {f'(\xi) \over f(\xi) - w }\,d\xi .\end{align*} Taking \(\rho ' < \min_{{\left\lvert {\xi} \right\rvert} = \rho} {\left\lvert {f(z)} \right\rvert}\) makes this a holomorphic function of \(w\) on \({\mathbb{D}}_{\rho'}(0)\), and as a continuous \({\mathbf{Z}}{\hbox{-}}\)valued function it is constant. Since \(F(0) = n\), this forces \(F(w) = n\) for all \({\left\lvert {w} \right\rvert} < \rho'\), so there are \(n\) solutions to \(f(z) = w\) in these discs. After shrinking these discs if necessary, \(f'\neq 0\) is nonvanishing on a punctured disc, so \(f\) is injective there and these solutions are distinct.