Idea: maximum modulus plus Rouche.
Open Mapping Theorem
Any holomorphic non-constant map is an open map.



Exercises
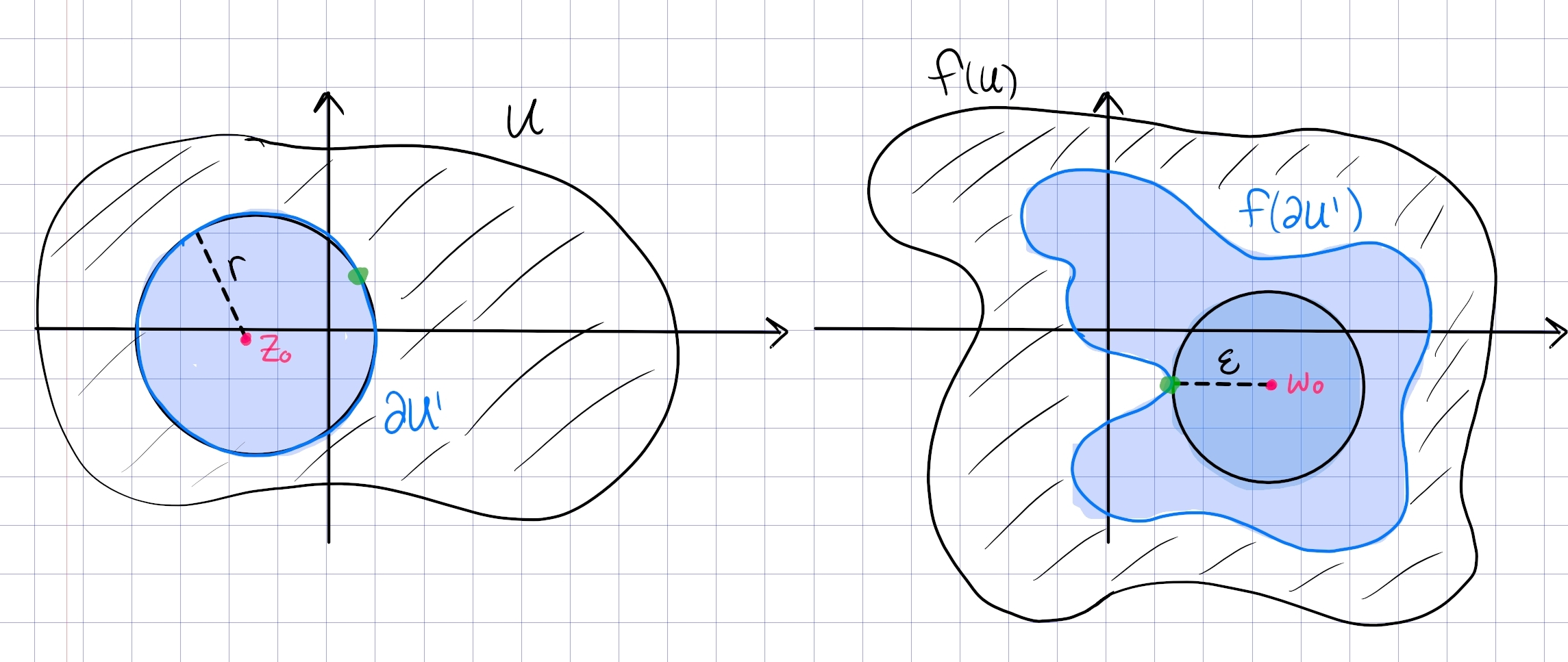
Show that there is no bijective conformal map from \(A\coloneqq\left\{{0< {\left\lvert {z} \right\rvert} < 1}\right\}\) to \(B\coloneqq\left\{{1<{\left\lvert {z} \right\rvert} < 2}\right\}\).
Suppose toward a contradiction that such an injective map \(f: A\to B\). Since \(f(A) \subseteq B\) which is bounded, \(f\) is bounded and thus any singularities in \(A\) are removable. So \(f\) extends holomorphically to \(F: {\mathbb{D}}\to \overline{B}\), and since \(F\) is an open map, \(F({\mathbb{D}}) \subseteq B\). Write \(w_0 \coloneqq F(0) \in B\), then by surjectivity there is a \(z_0\in A\) such that \(f(z_0) = w_0\). Since \(F = f\) on \(A\), we also have \(F(z_0) = w_0\). Since \(A\) is open, \(z_0\) is interior, and since \(z_0\neq 0\) we can separate \(z_0\) and zero by disjoint open sets \(U\) and \(V\). Since \(F\) is open, \(F(U), F(V)\) are open in \(B\) and contain \(w_0\). Then \(F(U) \cap F(V)\) is an open set containing \(w_0\), so there is a disc \(D_{\varepsilon}(w_0)\) in \(F(U)\) and \(F(V)\). But then \(F({\mathbb{D}}_{\varepsilon}(w_0))\) is an open set intersecting \(U\) and \(V\), contradicting that they were disjoint.
Prove that if \(f\) is holomorphic on a connected open set \(\Omega\) and \(f^2(z) = \overline{f(z)}\) then \(f\) is constant.
Write \(F(z) \coloneqq f^3(z)\) so that \begin{align*} F(z) = f^2(z) f(z) = \overline{f(z)}f(z) = {\left\lvert {f(z)} \right\rvert}^2 .\end{align*} Since \(F\) is also holomorphic on \(\Omega\) and this calculation shows \(F(\Omega) \subseteq \Omega\), \(F\) must be constant by the open mapping theorem. So \(f^3(z) = c\) for some \(c\), forcing \(f\) to be constant as well.