On strategy: see https://www.damtp.cam.ac.uk/user/reh10/lectures/nst-mmii-chapter5.pdf
A quick shortcut (?) for the quotient rule: \begin{align*} {\frac{\partial }{\partial z}\,} {p(z) \over q(z)} = {p'(z)\over q(z)} - {p(z)q'(z) \over q^2(z)} .\end{align*} Useful when taking \(z\to z_0\) with \(z_0\) a root of \(p, p', q'\).
Pedantic warning: \(\mathop{\mathrm{Res}}_{z=p}(f)\) should really be \(\mathop{\mathrm{Res}}_{z=p}(df)\) for \(df = f(z) \,dz\), since it’s only an invariant of the 1-form \(df\) and not necessarily \(f\) itself. We freely abuse notation!
Check: do you need residues at all?? You may be able to just compute an integral!
-
If the integrand is holomorphic throughout the region enclosed by \(\gamma\), \(\int_\gamma f = 0\)
-
If \(f\) has a well-defined primitive \(F\) on \(\gamma\), then \begin{align*} \int_\gamma f = \int_\gamma F' = F(\gamma(1)) - F(\gamma(0)) = 0 .\end{align*}
-
Use Cauchy’s theorem when applicable: \begin{align*} \int_\gamma {f(z) \over (z-a)^n} = 2\pi i f^{(n-1)}(a) .\end{align*}
-
Compute directly by parameterization: \begin{align*} \int_\gamma f \,dz= \int_a^b f(z(t))\, z'(t) \,dt&& \text{for } z(t) \text{ a parameterization of } \gamma ,\end{align*}
- Note: you can parameterize a circle around \(z_0\) using \begin{align*} z= z_0 + re^{i \theta } .\end{align*}
Residue Formulas
Let \(f\) be meromorphic on a region \(\Omega\) with poles \(\left\{{ { {z}_1, {z}_2, \cdots, {z}_{N}} }\right\}\). Then for any \(\gamma \in \Omega\setminus\left\{{ { {z}_1, {z}_2, \cdots, {z}_{N}} }\right\}\), \begin{align*} {1 \over 2\pi i } \int_\gamma f(z) \,dz= \sum_{j=1}^N n_\gamma(z_j) \mathop{\mathrm{Res}}_{z=z_j} f .\end{align*} If \(\gamma\) is a toy contour with winding number 1 about each pole, then \begin{align*} {1\over 2\pi i}\int_\gamma f\,dz= \sum_{j=1}^N \mathop{\mathrm{Res}}_{z=z_j}f .\end{align*}
If \(f\) has a pole \(z_0\) of order \(n\), then \begin{align*} \mathop{\mathrm{Res}}_{z=z_0} f = \lim_{z\to z_0} {1 \over (n-1)!} \qty{{\frac{\partial }{\partial z}\,}}^{n-1} (z-z_0)^n f(z) .\end{align*}
As a special case, if \(z_0\) is a simple pole of \(f\), then \begin{align*} \mathop{\mathrm{Res}}_{z=z_0}f = \lim_{z\to z_0} (z-z_0) f(z) .\end{align*}
If additionally \(f=g/h\) where \(h(z_0) = 0\) and \(h'(z_0)\neq 0\), \begin{align*} \mathop{\mathrm{Res}}_{z=z_0} {g(z) \over h(z)} = {g(z_0) \over h'(z_0)} .\end{align*}
Note that if \(f(z) = 1/h(z)\) and \(z_0\) is a simple pole, this reduces to \begin{align*} \mathop{\mathrm{Res}}_{z=z_0}{1\over h(z)} = {1\over h'(z_0)} .\end{align*}
Note that only the denominator gets differentiated, not the numerator! To remember this, just rederive the equation from L’Hopital’s rule and use the product rule on \((z-z_0)g(z)\).
Apply L’Hopital: \begin{align*} (z-z_0) {g(z) \over h(z)} = {(z-z_0) g(z) \over h(z) } \overset{LH}{=} {g(z) + (z-z_0) g'(z) \over h'(z)} \overset{z\to z_0}\longrightarrow{g(z_0) \over h'(z_0)} .\end{align*}
\begin{align*} \mathop{\mathrm{Res}}_{z=\infty}f(z) = \mathop{\mathrm{Res}}_{z=0} g(z) && g(z) \coloneqq-{1 \over z^2}f\qty{1\over z} .\end{align*}
Note on where this weird formula comes from: residues are associated not to function \(f\) but to differential forms \(f(z)\,dz\), and inversion sends \(f(z) \,dz\to f(1/z)d(1/z) = f(1/z)\cdot -{1\over z^2}\,dz\). This residue can alternatively be calculated for \(f\) by taking \(\gamma\) a contour enclosing all singularities of \(f\) and computing \begin{align*} \mathop{\mathrm{Res}}_{z=\infty}f(z) = -{1\over 2\pi}\int_\gamma f(z) \,dz .\end{align*}
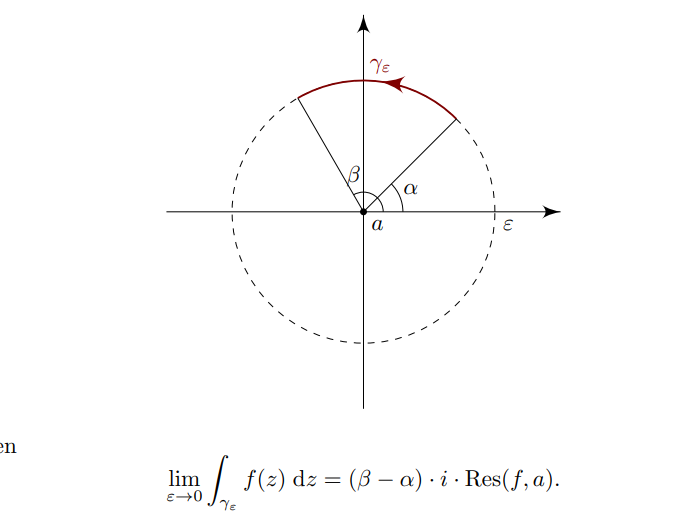
If \(z_0\) is an order 1 pole of \(f\) and \(\gamma_{{\varepsilon}, \theta}\) is an arc of the circle \(C_{\varepsilon}\coloneqq\left\{{ {\left\lvert {z-z_0} \right\rvert} = {\varepsilon}}\right\}\) subtending an angle of \(\theta\), then \begin{align*} \lim_{{\varepsilon}\to 0} \int_{\gamma_{{\varepsilon}, \theta}} f(z) \,dz= i\theta \mathop{\mathrm{Res}}_{z = z_0}f(z) .\end{align*}

Exercises
Avoiding Residue Formulas
Show that \begin{align*} \int_{S^1}z^k \,dz= \begin{cases} 2\pi i & k=-1 \\ 0 & \text{else}. \end{cases} ,\end{align*} and thus \begin{align*} \int \sum_{k\geq -M} c_k z^k = \sum_{k\geq -M} \int c_k z^k = 2\pi i c_{-1} ,\end{align*} i.e. the integral picks out the \(c_{-1}\) coefficient in a Laurent series expansion.
\begin{align*} \int_\gamma z^k \,dz= \int_0^{2\pi} e^{ik\theta} ie^{i\theta } \,d\theta= i\int_0^{2\pi} e^{i(k+1)\theta \,d\theta} = \begin{cases} 2\pi i & k=-1 \\ 0 & \text{else}. \end{cases} \end{align*}
Compute the following integrals: \begin{align*} \int_{{\left\lvert {z-1} \right\rvert} = 1} {1\over z^2-1} \,dz\\ \int_{{\left\lvert {z-0} \right\rvert} = 2} {1\over z^2-1} \,dz\\ .\end{align*} Compute the 2nd integral by finding a primitive.
For the first integral: \begin{align*} \int_\gamma{1\over z^2-1}\,dz &= {1\over 2}\int_\gamma {1\over z-1} + {1\over z+1}\,dz\\ &= {1\over 2}\int_\gamma {1\over z-1} \\ &= {1\over 2}\cdot 2\pi i \mathop{\mathrm{Res}}_{z=1}f(z) \\ &= {1\over 2}\cdot 2\pi i \cdot 1 \\ &= \pi i ,\end{align*} using that \(f(z) = {1\over z-1}\) is already an expansion of \(f\) about \(z=1\) since it is a Laurent series in \((z-1)^k\), so the residue is \(1\).
For the second integral: attempt to define a primitive \begin{align*} F(z) \coloneqq{1\over 2}\log\qty{z-1\over z+1} \implies F'(z) = {1\over z^2-1} .\end{align*} If this primitive is well-defined on \(\gamma\), the integral will vanish because this is a closed curve. Choose the branch cut \({\mathbf{C}}\setminus(-\infty, 0]\) and define \(g(z) = {z-1\over z+1}\), so that \(F(z) = {1\over 2}\log(g(z))\). Then then \(g(z)\in (-\infty, 0] \iff z\in [-1, 1]\), and this is well-defined on \(\gamma\) since \([-1, 1]\) does not intersect \(\gamma\).
Thus for \(\gamma\) any parameterization of \({\left\lvert {z} \right\rvert} = 2\), \begin{align*} \int_{{\left\lvert {z} \right\rvert} = 2} f(z) \,dz = \int_{{\left\lvert {z} \right\rvert} = 2} F'(z)\,dz = F(\gamma(0)) - F(\gamma(1)) = 0 .\end{align*}
Compute \begin{align*} \int_{S^1} {2 \sinh(z) \over z^n}\,dz .\end{align*}
Write \(f(z) = 2\sinh(z) = e^{z} - e^{-z}\) and apply the generalized Cauchy formula: \begin{align*} f^{(n-1)}(0) &= {(n-1)! \over 2\pi i} \int_{S^1} {f(z) \over (z-0)^n}\,dz\\ \\ \implies \int_{S^1}{f(z)\over z^n}\,dz &= {2\pi i \over (n-1)!} f^{(n-1)}(0) \\ &= {2\pi i\over (n-1)!} 2\cdot \qty{e^z - (-1)^{n-1} e^z \over 2}\Big|_{z=0} \\ &= {2\pi i\over (n-1)!} 2\cdot \qty{1 + (-1)^{n} \over 2} \\ &= \begin{cases} {2\pi i \over (n-1)!} & n \text{ even } \\ 0 & n \text{ odd }. \end{cases} .\end{align*}
Compute \begin{align*} \int_\gamma {z^2+1 \over z(z^2 + 4)}\,dz \end{align*} for
- A circle of radius \(1\),
- A circle of radius \(2+{\varepsilon}\),
For the smaller circle, use Cauchy’s formula \begin{align*} \int_{{\left\lvert {z} \right\rvert} = 1} f(z) \,dz &= \int_{{\left\lvert {z} \right\rvert} = 1} { {z^2 + 1 \over z^2 + 4} \over z} \,dz\\ &= 2\pi i \qty{z^2 + 1 \over z^2 + 4} \Big|_{z=0} \\ &= {i\pi \over 2} .\end{align*} .
For the larger circle, break into principal parts. Write \begin{align*} {z^2 + 1 \over z(z^2+4)} = {a\over z} + {b\over z+2i} + {c\over z-2i} ,\end{align*} and use PFD/cover-up method/finding residues:
- \(a = \qty{z^2+1\over z^2+4}\Big|_{z=0} = {1\over 4}\)
- \(b= \qty{z^2 + 1 \over z(z-2i)}\Big|_{z=-2i} = {-4+1\over -2i(-4i)} = {3\over 8}\)
- \(c = \qty{z^2 + 1 \over z(z+2i)}\Big|_{z=2i} = {-4+1 \over 2i(4i)} = {3\over 8}\)
Thus \begin{align*} \int_\gamma f(z) \,dz &= \int_\gamma \qty{ {1/4\over z} + {3/8\over z+2i} + {3/8 \over z-2i} } \,dz\\ &= 2\pi i\qty{ {1\over 4} + {3\over 8} + {3\over 8}} .\end{align*}
Find all residues of the following function by writing it as a sum of principal parts at its poles: \begin{align*} f(z) = {z^3 \over z^2 + 1} .\end{align*}
Use polynomial long division to write \begin{align*} z^3 = z(z^2+1) - z \implies {z^3 \over z^2 + 1} = z - {z\over z^2 + 1} .\end{align*} Factor the latter part: \begin{align*} {z\over z^2 + 1} = {a\over z+i} + {b\over z-i} \implies a(z-i) + b(z+i) = z ,\end{align*} evaluate at \(z=i\) to get \(b=1/2\), and at \(z=-i\) to get \(a=1/2\). Thus \begin{align*} f(z) = z - {1/2 \over z+i} - {1/2 \over z-i} = P_\infty + P_{-i} + P_{i} ,\end{align*} yielding poles at \(\pm i\) with residues \begin{align*} \mathop{\mathrm{Res}}_{z=\infty} f(z) &= -1 \\ \mathop{\mathrm{Res}}_{z = i} f(z) &= -1/2 \\ \mathop{\mathrm{Res}}_{z = -i} f(z) &= -1/2 \\ .\end{align*}
Use a direct Laurent expansion to show \begin{align*} \mathop{\mathrm{Res}}_{z=0} {1\over z-\sin(z)} = {3! \over 5\cdot 4} .\end{align*}
Note the necessity: one doesn’t know the order of the pole at zero, so it’s unclear how many derivatives to take.
Expand: \begin{align*} {1\over z - \sin(z)} &= z^{-1}\qty{1 - z^{-1}\sin(z) }^{-1}\\ &= z^{-1}\qty{1 - z^{-1}\qty{ z - {1\over 3!}z^3 + {1\over 5!} z^5 - \cdots}}^{-1}\\ &= z^{-1}\qty{1 - \qty{ 1 - {1\over 3!}z^2 + {1\over 5!} z^4 - \cdots}}^{-1}\\ &= z^{-1}\qty{{1\over 3!}z^2 - {1\over 5!}z^4 + \cdots}^{-1}\\ &= z^{-1}\cdot 3! z^{-2} \qty{1 - {1\over 5!/3!}z^2 + \cdots}^{-1}\\ &= {3!\over z^3} \qty{1 \over 1 - \qty{ {1\over 5\cdot 4}z^2 + \cdots}} \\ &= {3!\over z^3}\qty{1 + \qty{{1\over 5\cdot 4}z^2} + \qty{{1\over 5\cdot 4}z^2}^2 + \cdots} \\ &= 3! z^{-3} + {3!\over 5\cdot 4}z^{-1}+ O(z) \\ .\end{align*}
Compute \begin{align*} \mathop{\mathrm{Res}}_{z=0} {1\over z^2 \sin(z)} .\end{align*}
First expand \((\sin(z))^{-1}\): \begin{align*} {1\over \sin(z)} &= \qty{z - {1\over 3!}z^3 + {1\over 5!}z^5 -\cdots }^{-1}\\ &= z^{-1}\qty{1 - {1\over 3!}z^2 + {1\over 5!}z^4 - \cdots }^{-1}\\ &= z^{-1}\qty{1 + \qty{{1\over 3!}z^2 - {1\over 5!} z^4 + \cdots} + \qty{{1\over 3!}z^2 - \cdots}^2 + \cdots } \\ &= z^{-1}\qty{1 + {1\over 3!}z^2 \pm O(z^4) } ,\end{align*} using that \((1-x)^{-1}= 1 + x + x^2 + \cdots\).
Thus \begin{align*} z^{-2}\qty{\sin(z)}^{-1} &= z^{-2} \cdot z^{-1}\qty{1 + {1\over 3!}z^2 \pm O(z^4) } \\ &= z^{-3} + {1\over 3!}z^{-1}+ O(z) .\end{align*}
Applying the formulas
Use the rational function formula to compute the residues at \(z=\pm i\) of \begin{align*} f(z) \coloneqq{1\over z^2 + 1} .\end{align*}
Applying the rational function formula: \begin{align*} \mathop{\mathrm{Res}}_{z=z_0}{1\over 1+z^2} &= {1\over 2z}\Big|_{z= z_0} \implies\\ \mathop{\mathrm{Res}}_{z=i}f(z) &= {1\over 2i} = -{i\over 2} \\ \mathop{\mathrm{Res}}_{z=-i}f(z) &= -{1\over 2i} = {i\over 2} .\end{align*}
Find the residue at \(\omega_n \coloneqq e^{\pi i \over n}\) of \begin{align*} f(z) = {1\over z^n + 1} .\end{align*}
Check that \({\frac{\partial }{\partial z}\,} z^n+1 = nz^{n-1}\neq 0\) for \(z\neq 0\), so this has no repeated roots since \(z=0\) is not a root. Thus all of the poles are simple, so apply the rational function formula: \begin{align*} \mathop{\mathrm{Res}}_{z=\zeta_{m}} {1\over z^n + 1} &= {1 \over nz^{n-1}}\Big|_{z=\omega_n} \\ &= {1\over n\omega_n^{n-1}} \\ &= {\omega_n^{1-n}\over n} \\ &= -{\omega_n \over n} ,\end{align*} which follows from expanding \begin{align*} \omega_n^{1-n} = e^{i\pi (1-n) \over n} = e^{i\pi\over n}e^{-i\pi n \over n} = e^{i\pi \over n}\cdot (-1) = -\omega_n .\end{align*} .
Compute \begin{align*} &\mathop{\mathrm{Res}}_{z=\infty}e^z\\ &\mathop{\mathrm{Res}}_{z=\infty}{z-1\over z+1} .\end{align*}
In parts:
-
For \(e^z\):
- Integral formula: \(\mathop{\mathrm{Res}}_{z=\infty}f(z) = -{1\over 2\pi }\int_\gamma f(z)\,dz\) where \(\gamma\) encloses all singularities of \(f\), but \(e^z\) is entire, so this integral is zero and thus the residue is zero.
- Inversion formula: expand \(z^{-2}f(1/z)\) about \(z=0\) to obtain \begin{align*} {1\over z^2}e^{1\over z} = z^{-2}\sum_{k\geq 0}z^{-k}/k! = \sum_{k\geq 0}z^{-k-2}/k! = z^{-2} + z^{-3} + {1\over 2!}z^{-4} + { \mathsf{O}}(z^{-5}) ,\end{align*} so the residue is zero.
-
For \({z+1\over z-1}\):
- Integral formula: \begin{align*} \mathop{\mathrm{Res}}_{z=\infty} &= -{1\over 2\pi}\int_{{\left\lvert {z} \right\rvert} = 2} {z-1\over z+1}\,dz\\ &= - \mathop{\mathrm{Res}}_{z=-1} {z-1\over z+1} \\ &= - (-2) \\ &= 2 .\end{align*}
- Inversion formula: \begin{align*} {1\over z^2}{ z^{-1}- 1 \over z^{-1}+ 1} &= z^{-2}{1 - z \over 1 + z} \\ &= z^{-2}(z-1)\sum_{k\geq 0} (-z)^k \\ &= z^{-2} + 2z^{-1}-2 + 2z - { \mathsf{O}}(z^2) ,\end{align*} which has residue 2.