Residues
Use residues at infinity to evaluate \begin{align*} \int_{|z|=1} \frac{1}{(z-2)(1+2 z)^{4}(1-3 z)^{7}} \,dz .\end{align*}
Rational Functions
Superlinear Decay
\begin{align*} \int_{\mathbf{R}}{1 \over x^4 + 1} = {\pi \sqrt{2} \over 2} = {\pi \over \sqrt 2} .\end{align*}
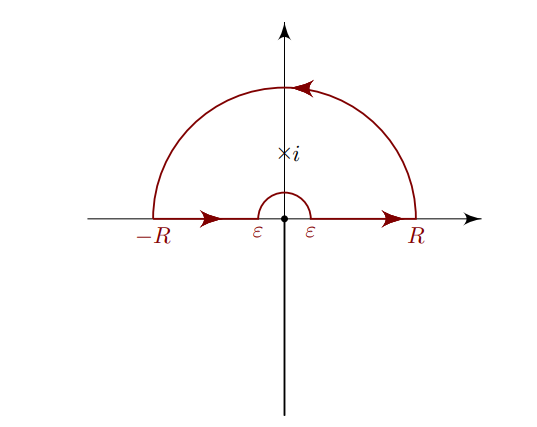
The integrand \(f\in { \mathsf{O}}\qty{1\over z^4} \subseteq { \mathsf{O}}\qty{1\over z^{1+{\varepsilon}}}\), so a semicircular contour works. Factoring the denominator: find a principal root \begin{align*} \omega^4 = -1 = e^{i\pi} \implies \omega = e{i\pi\over 4} ,\end{align*} so \begin{align*} z^4 + 1 = (z-\omega)(z-\omega\zeta_4)(z-\omega\zeta_4^2)(z-\omega\zeta_4^3) \leadsto {\pi \over 4}, {3\pi \over 4}, {5\pi \over 4}, {7\pi \over 4} .\end{align*} So there are two simple poles in \({\mathbb{H}}\):

Write them as \(z_1 = e^{i\pi \over 4}\) and \(z_2 = e^{3 i \pi \over 4}\). Computing the residues: \begin{align*} \mathop{\mathrm{Res}}_{z=z_k} f(z) &= \lim_{z\to z_k} {z-z_k \over z^4 + 1} \\ &{ \overset{\scriptscriptstyle\text{LH}}{=} }\lim_{z\to z_k} {1\over 4z^3} \\ &= {4z^{-3} }\Big|_{z=z_k} ,\end{align*} so \begin{align*} 2\pi i \sum \mathop{\mathrm{Res}}_{z=z_k} &= {2\pi i \over 4}\qty{z_1^{-3} + z_2^{-3}} \\ &= {\pi i \over 2}\qty{e^{-3 i \pi \over 4} + e^{-9 i \pi \over 4}} \\ &= {\pi i \over 2}\qty{e^{-3 i \pi \over 4} + e^{-i \pi \over 4}} \\ &= {\pi i \over 2}\cdot e^{-2i\pi \over 4}\qty{e^{- i \pi \over 4} + e^{i \pi \over 4}} \\ &= \pi i\, {1\over i} \cos\qty{\pi \over 4} \\ &= {\pi \sqrt 2 \over 2} .\end{align*}
\begin{align*} I \coloneqq\int_0^\infty {1\over x^4 + 1 }\,dx= {\pi \over 2\sqrt 2} .\end{align*}
Note that the function is even, so \begin{align*} \int_{0^\infty} f(x) \,dx= {1\over 2} \int_{\mathbf{R}}f(x)\,dx= {1\over 2} {\pi \over \sqrt 2} = {\pi \over 2 \sqrt 2} ,\end{align*} using the solution from a previous problem.
A sector will work, since there is a symmetry under \(z\to \zeta_4 z\) and \(f(z) \sim z^{-4}\), so the semicircular piece will vanish. Take the contour \(\Gamma\) comprised of
- \(\gamma_1: \left\{{t + 0i {~\mathrel{\Big\vert}~}t\in [0, R]}\right\}\),
- \(C_R: \left\{{Re^{it}{~\mathrel{\Big\vert}~}t\in [0, \pi/2]}\right\}\),
- \(\gamma_2: \left\{{0 + it {~\mathrel{\Big\vert}~}t\in [0, R]}\right\}\),
oriented counter-clockwise. Note that \(z^4+1 = \prod_{k=0}^3 (z-\omega \zeta_4)\) where \(\omega = e^{i\pi \over 4}\) and \(\zeta_4 = e^{2\pi i\over 4} = i\), so there is only one pole at \(z_0 \coloneqq e^{i\pi\over 4}\) within this contour.
Computing the symmetry: \begin{align*} \int_{\gamma_2} f(z) \,dz &= \int_R^0 {i \over (ti)^4 + 1}\,dt\qquad z=ti,\, \,dz= i\,dt\\ &= -i \int_0^R {1\over t^4 + 1}\,dt\\ &= -i \int_{\gamma_1} f(z) \,dz ,\end{align*} so applying the residue theorem and noting that \(\int_{C_R}f\to 0\), \begin{align*} 2\pi \mathop{\mathrm{Res}}_{z=z_0} f(z) = \int_\Gamma f(z) \,dz= \qty{\int_{\gamma_1} + \int_{C_R} + \int_{\gamma_2}}f \longrightarrow(1-i) I .\end{align*} Computing the residue: \begin{align*} \mathop{\mathrm{Res}}_{z=z_0}f(z) &= {1\over 4z^3}\Big|_{z= e^{i\pi \over 4}} \\ &= {1\over 4}e^{-3i\pi \over 4} \\ &= {1\over 4}e^{5i\pi \over 4} .\end{align*}
Thus \begin{align*} I &= (1-i)^{-1}2\pi i \mathop{\mathrm{Res}}_{z=z_0} f(z) \\ &= \qty{\overline{1-i} \over {\left\lvert {1-i} \right\rvert}^2} 2\pi i \cdot {1\over 4}e^{5i\pi \over 4} \\ &= {1+i \over 2} {\pi i \over 2}e^{5i\pi \over 4} \\ &= {e^{i\pi \over 4} \over \sqrt{2} } {\pi i \over 2}e^{5i\pi \over 4} \\ &= {\pi i \over 2\sqrt{2}}e^{6i\pi \over 4} \\ &= {\pi i \over 2\sqrt{2}}(-i) \\ &= {\pi \over 2\sqrt{2}} .\end{align*}
Consider the auxiliary function \(g(z) \coloneqq\log(z) f(z)\), and take a keyhole contour:
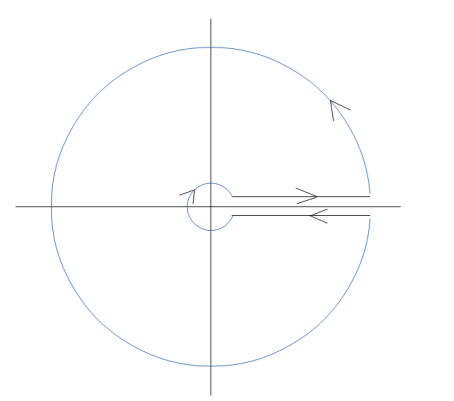
Let \(\Gamma\) be the counterclockwise contour consisting of
- \(C_{\varepsilon}= \left\{{{\varepsilon}e^{it}{~\mathrel{\Big\vert}~}t\in [0+{\varepsilon}, 2\pi - {\varepsilon}]}\right\}\)
- \(\gamma_+ = \left\{{x+i{\varepsilon}{~\mathrel{\Big\vert}~}x\in [{\varepsilon}, R]}\right\}\)
- \(C_R= \left\{{R e^{it}{~\mathrel{\Big\vert}~}t\in [0+{\varepsilon}, 2\pi - {\varepsilon}]}\right\}\)
- \(\gamma_- = \left\{{x-i{\varepsilon}{~\mathrel{\Big\vert}~}x\in [{\varepsilon}, R]}\right\}\)
Computing the symmetry: \begin{align*} \int_{\gamma_-}{\log(z) \over z^{4} + 1} \,dz &= \int_{R}^{\varepsilon}{\log(x-i{\varepsilon}) \over (x-i{\varepsilon})^4 + 1} \,dx\qquad z=x-i{\varepsilon}, \,dz= \,dx\\ &\to - \int_{{\varepsilon}}^R {\log(x) + 2\pi i\over x^4 + 1}\,dz\\ &= -\int_{\gamma_+} {\log(z) \over z^4+1}\,dz- 2\pi i\int_{\gamma_+} {1\over z^4+1} \,dz ,\end{align*} so \begin{align*} \int_{\gamma_+} f + \int_{\gamma_-}f \longrightarrow-2\pi i I .\end{align*} By the ML estimate, since \(\log(z)/z^4\to 0\) as \({\left\lvert {z} \right\rvert}\to \infty\), \(\int_{C_R}g(z) \to 0\). Similarly, since \(\log(z) / (z^4+1)\to 0\) as \({\left\lvert {z} \right\rvert}\to 0\), \(\int_{C_{\varepsilon}}\to 0\). We’re then left with the sum of residues at \(e^{k i \pi \over 4}\) for \(k = 1,3,5,7\). We have \begin{align*} \mathop{\mathrm{Res}}_{z=z_k} f(z) &= {1\over 4z^3}\Big|_{z=z_k} \\ &= {z\over 4z^4}\Big|_{z=z_k} \\ &= - {z\over 4}\Big|_{z=z_k} \qquad \text{ since } z_k^4 = -1 \\ &= -{z_k \over 4} ,\end{align*} so \begin{align*} \mathop{\mathrm{Res}}_{z=z_k}g(z) = -{z_k \over 4}\log(z_k) .\end{align*}
Now use that in the limit, \begin{align*} 2\pi i \sum_k \mathop{\mathrm{Res}}_{z=z_k}g(z) &= \int_\Gamma g(z) \,dz\\ &= \qty{\int_{\gamma_+} + \int_{\gamma_i}} f \\ &= -2\pi i I ,\end{align*} so \(I = -\sum_k \mathop{\mathrm{Res}}_{z=z_k} g(z)\).
Being very careful to note that we’ve chosen a branch of \(\log\) where \(\operatorname{Arg}(z) \in (0, 2\pi)\) in order to get the signs right, \begin{align*} -\sum_k \mathop{\mathrm{Res}}(z=z_k) g(z) &= {1\over 4}\qty{ z_1\log(z_1) + z_2\log(z_2)+z_3\log(z_3)+z_4\log(z_4) } \\ &= {1\over 4}\qty{ z_1 {i\pi \over 4} + z_2 {3i\pi \over 4} + z_3 {5i\pi \over 4}+ z_4 {7i\pi \over 4} } \\ &= {i\pi \over 16}\qty{ z_1 + 3z_2 + 5z_3+ 7z_4 } \\ &= {i\pi \over 16}\qty{ \omega \zeta_4^0 + 3\omega\zeta_4^1 + 5\omega\zeta_4^2+ 7\omega \zeta_4^3 } \\ &= {i\pi \omega \over 16}\qty{ 1 + 3i + -5 + -7i } \\ &= {i\pi \omega \over 16}(-4-4i) \\ &= -{i\pi \omega \over 4}(1+i) \\ &= -{i\pi \omega \over 2}{ \omega \over \sqrt{2} } \\ &= -i\omega^2 {\pi \over 2 \sqrt 2} \\ &= {\pi \over 2\sqrt{2} } ,\end{align*} using that \({\sqrt 2\over 2}(1+i) = e^{i\pi \over 4} = \omega\) and \(\omega^2 = i\).
\begin{align*} \int_{\mathbf{R}}{1 \over (1+x^2)^2} = {\pi \over 2} .\end{align*}
Use that \(f(z) \sim 1/z^4\):

Then \begin{align*} \int_{C_1 + C_R} f = \int_{C_1} f + \int_{C_R} f = 2\pi i \mathop{\mathrm{Res}}_{z=i} {1\over (1+z^2)^2} .\end{align*}
Note \(f\) factors: \begin{align*} f(z) = {1 \over \qty{(z-i)(z+i)}^2 } ,\end{align*} so \(z=i\) is a pole of order 2.
Compute the residue within the contour: \begin{align*} \mathop{\mathrm{Res}}_{z=i} f(z) = \lim_{z\to i} {\frac{\partial }{\partial z}\,} {1\over (z+i)^2} = - {2 \over (z+i)^3 }\Big|_{z=i} = - {2\over (2i)^3 } = {1\over 4i} = -{i\over 4} .\end{align*}
Now solve: \begin{align*} 2\pi i \qty{- {i\over 4}} = \int_{C_1}f + \int_{C_R} f \coloneqq I_R + \int_{C_R}f \implies I_R = {\pi \over 4} - \int_{C_R} f .\end{align*}
Note \(I_R \overset{R\to \infty}\longrightarrow I \coloneqq\int_{\mathbf{R}}f\), so it suffices to show the semicircular error term vanishes as \(R\to \infty\). Parameterize \(C_R = \left\{{z=R e^{it} {~\mathrel{\Big\vert}~}t\in [0, \pi]}\right\}\), so \({\left\lvert {z} \right\rvert} = R\) on \(C_R\). Letting \(z=e^{it}\), \(\,dz=iR e^{it}\,dt\), \begin{align*} {\left\lvert {\int_{C_R} f(z) \,dz} \right\rvert} &= {\left\lvert {\int_{C_R} {1\over (1+z^2)^2} \,dz} \right\rvert} \\ &\leq \int_{C_R}{\left\lvert { {1\over (1+z^2)^2} } \right\rvert} \,dz\\ &= \int_{C_R} {1\over {\left\lvert {1+z^2} \right\rvert}^2 } \,dz\\ &\leq \int_{C_R} {1\over \qty{1 - {\left\lvert {z} \right\rvert}^2 }^2 } \,dz\\ &= \int_{C_R} {1\over \qty{1 - R^2 }^2 } \,dz\\ &= {1\over \qty{1 - R^2 }^2 } \int_{C_R} \,dz\\ &= {1\over \qty{1 - R^2 }^2 } \cdot \mathop{\mathrm{length}}(C_R) \\ &= {1\over \qty{1 - R^2 }^2 } \cdot \qty{1\over 2}2\pi R \\ &= {\pi R \over R^4 + O(R^3)} \\ &= \pi\qty{ 1 \over R^3 + O(R^2)} \\ &\overset{R\to\infty}\longrightarrow 0 ,\end{align*} where we’ve used a variant of the triangle inequality: \begin{align*} {\left\lvert {a\pm b} \right\rvert} \geq {\left\lvert { {\left\lvert {a} \right\rvert} - {\left\lvert {b} \right\rvert} } \right\rvert} \implies {1\over {\left\lvert {a \pm b} \right\rvert}} \leq {1\over {\left\lvert {a} \right\rvert} - {\left\lvert {b} \right\rvert} } .\end{align*}
- Factor \((1+z^2)^2 = ((z-i)(z+i))^2\), so \(f\) has poles at \(\pm i\) of order 2.
- Take a semicircular contour \(\gamma \coloneqq I_R \cup D_R\), then \(f(z) \approx 1/z^4 \to 0\) for large \(R\) and \(\int_{D_R} f \to 0\).
- Note \(\int_{I_R} f \to \int_{\mathbf{R}}f\), so \(\int_\gamma f \to \int_{\mathbf{R}}f\).
- \(\int_\gamma f = 2\pi i \sum_{z_0} \mathop{\mathrm{Res}}_{z=z_0} f\), and \(z_0 = i\) is the only pole in this region.
- Compute \begin{align*} \mathop{\mathrm{Res}}_{z=i} f &= \lim_{z\to i} {1\over (2-1)!} {\frac{\partial }{\partial z}\,} (z-i)^2 f(z) \\ &= \lim_{z\to i} {\frac{\partial }{\partial z}\,} {1\over (z+i)^2 } \\ &= \lim_{z\to i} {-2 \over (z+i)^3 } \\ &= -{2 \over (2i)^3 } \\ &= {1\over 4i} \\ \\ \implies \int_\gamma f &= {2\pi i \over 4i} = \pi/2 ,\end{align*}
\begin{align*} I \coloneqq\int_{-\infty}^{\infty} \frac{d x}{\left(1+x^{2}\right)^{n+1}}=\frac{(2 n) !}{4^{n}(n !)^{2}} \pi . \end{align*}
Note that this solution can be written many ways: \begin{align*} I = {2n \choose n} {\pi \over 4^n} = { \qty{2n}_{ (n) } \over n!} {\pi \over 4^n} = {(2n)(2n-1)\cdots(n+1)\over n!} {\pi \over 4^n} .\end{align*}
The integrand is \(f\in { \mathsf{O}}\qty{1\over z^{2n+2}} \subseteq { \mathsf{O}}\qty{1\over z^{1+{\varepsilon}}}\), so a semicircular contour will work:
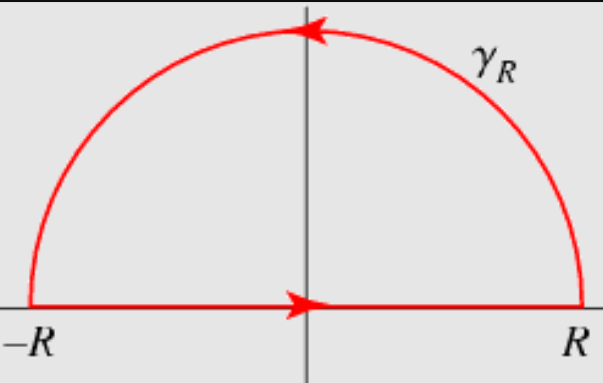
Thus \begin{align*} I &= 2\pi i \sum_{z_k \in {\mathbb{H}}} \mathop{\mathrm{Res}}_{z=z_k} {1\over (1+z^2)^{n+1}} \\ &= 2\pi i \mathop{\mathrm{Res}}_{z=i} {1\over (z+i)^{n+1}(z-i)^{n+1} } \\ &= 2\pi i \lim_{z\to i}{1\over n!}\qty{{\frac{\partial }{\partial z}\,}}^n (z+i)^{-(n+1)} \\ &= 2\pi i \lim_{z\to i}{1\over n!}\qty{{\frac{\partial }{\partial z}\,}}^{n-1} -(n+1)(z+i)^{-(n+2)} \\ &= 2\pi i \lim_{z\to i}{1\over n!}\qty{{\frac{\partial }{\partial z}\,}}^{n-2} -(n+1) \cdot -(n+2) (z+i)^{-(n+3)} \\ &= \qquad \vdots \\ &= 2\pi i \lim_{z\to i}{1\over n!}\qty{{\frac{\partial }{\partial z}\,}}^{n-k} (-1)^k (n+1)(n+2)\cdots(n+k) (z+i)^{-(n+k-1)} \\ &= \qquad \vdots \\ &= 2\pi i \lim_{z\to i} {1 \over n!}(-1)^n (n+1)(n+2)\cdots(2n)(z+i)^{-(2n-1)} \\ &= { \qty{2n}_{ (n) } \over n!} 2\pi i (-1)^n (2i)^{-(2n-1)} \\ &= { \qty{2n}_{ (n) } \over n!} 2\pi i (-1)^n {1\over 2^{2n+1} i^{2n+1}} \\ &= { \qty{2n}_{ (n) } \over n!} \pi (-1)^n {1\over 4^n i^{2n}} \\ &= { \qty{2n}_{ (n) } \over n!} \pi (-1)^n {1\over 4^n (-1)^n } \\ &= { \qty{2n}_{ (n) } \over n!} {\pi \over 4^n } .\end{align*}
\begin{align*} I\coloneqq\int_{\mathbf{R}}{x\over (x^2 + 4x+13)^2}\,dx .\end{align*}
Write the integrand as \(f\).
\(f\in { \mathsf{O}}\qty{1\over z^{3}} \subseteq { \mathsf{O}}\qty{1\over z^{1+{\varepsilon}}}\) means that a semicircular contour will work:
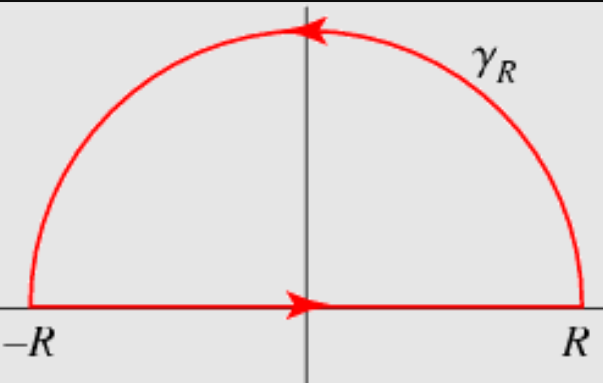
A quick justification: for \(R>1\), if \(n>k\) then \({\left\lvert {z} \right\rvert}^n > {\left\lvert {z} \right\rvert}^k\), so using the reverse triangle inequality, \begin{align*} {\left\lvert {z\over (z^2 + 4z + 13)^2} \right\rvert} &= {\left\lvert {z\over z^4 + 8z^3 + 42z^2 + 104z + 169} \right\rvert}\\ &\leq {\left\lvert {z\over {\left\lvert {z} \right\rvert}^4 - 8{\left\lvert {z} \right\rvert}^3 - 42{\left\lvert {z} \right\rvert}^2 - 104{\left\lvert {z} \right\rvert} - 169} \right\rvert}\\ &\leq {\left\lvert {z\over {\left\lvert {z} \right\rvert}^4 - 8{\left\lvert {z} \right\rvert}^4 - 42{\left\lvert {z} \right\rvert}^4 - 104{\left\lvert {z} \right\rvert}^4 - 169{\left\lvert {z} \right\rvert}^4} \right\rvert}\\ &= {\left\lvert {z\over {\left\lvert {z} \right\rvert}^4( 1 - 8 - 42 - 104 - 169)} \right\rvert}\\ &= 322 {{\left\lvert {z} \right\rvert} \over {\left\lvert {z} \right\rvert}^4} \\ &= 322 {\left\lvert {z} \right\rvert}^{-3} \\ &= 322 R^{-3} \to 0 \text{ as } R\to\infty .\end{align*}
Factor the denominator: \begin{align*} x^2 + 4x + 13 = 0 &\implies x^2 + 4x + \qty{4\over 2}^2 = -13 + \qty{4\over 2}^2 \\ &\implies (x+2)^2 = -9 \\ &\implies x = -2 \pm 3i ,\end{align*} one of which is in \({\mathbb{H}}\). Write these as \begin{align*} z_1 \coloneqq-2+3i && z_2 \coloneqq-2 - 3i .\end{align*}
So let \(\Gamma\) be comprised of
- \(C_1 = [-R,R]\),
- \(C_2 = \left\{{Re^{it} {~\mathrel{\Big\vert}~}t\in [0, \pi]}\right\}\),
- \(\Gamma = C_1 + C_2\), then \begin{align*} 2\pi i \sum_{z_k\in {\mathbb{H}}} \mathop{\mathrm{Res}}_{z=z_k}f(z) = \int_\Gamma f = \qty{\int_{C_1} + \int_{C_2}}f ,\end{align*} where \(\int_{C_2} f\to 0\) and \(\int_{C_1} f\to I\). So in the limit, \(I = 2\pi i \mathop{\mathrm{Res}}_{z=z_1} f(z)\). Computing this residue: note \(z_1\) is a pole of order 2, so \begin{align*} \mathop{\mathrm{Res}}_{z=z_1} &= \lim_{z\to z_1} {\frac{\partial }{\partial z}\,} (z-z_1)^2f(z) &= \lim_{z\to z_1} {\frac{\partial }{\partial z}\,} {z \over (z-z_2)^2} \\ &= \lim_{z\to z_1} { (z-z_2)^2 - 2z(z-z_2 ) \over (z-z_2)^4} \\ &= \lim_{z\to z_1} { (z-z_2) - 2z \over (z-z_2)^3} \\ &= \lim_{z\to z_1} -{ z+z_2 \over (z-z_2)^3} \\ &= - {z_1 + z_2 \over (z_1 - z_2)^2}\\ &= - {z_1 + \overline{z_1} \over (z_1 - \overline{z_1} )^2}\\ &= - {2\Re(z_1) \over (2i\Im(z_1))^3} \\ &= - {2\cdot (-2) \over (2i\cdot 3) ^3} \\ &= {4\over 2^3 \cdot 3^3 \cdot i^3} \\ &= {-i \over 2 \cdot 3^3 i^2} \\ &= {i\over 54} ,\end{align*} so \begin{align*} I = 2\pi i \cdot {i\over 54} = -{\pi \over 27} .\end{align*}
\begin{align*} I \coloneqq\int_{0}^{\infty} \frac{\cos (x)}{x^{2}+b^{2}} d x=\frac{\pi \mathrm{e}^{-b}}{2 b} .\end{align*}
The integrand is even, so \begin{align*} I = \Re{1\over 2} \tilde I \coloneqq{1\over 2} \int_{\mathbf{R}}{e^{iz} \over (z+ib)(z-ib)} \end{align*}
Since \(f \sim 1/x^2\), the ML estimate on a semicircular contour works:

Then \(\int_{C_R} f\to 0\) and \(\int_{C_1} f\to \tilde I\). Thus \begin{align*} \tilde I &= 2\pi i \mathop{\mathrm{Res}}_{z=ib} \\ &= 2\pi i \lim_{z\to ib}{e^{iz}\over (z+ib)} \\ &= 2\pi i {e^{-b} \over 2i b} \\ &= {\pi e^{-b} \over b} \end{align*} and \begin{align*} I = \Re {1\over 2} \tilde I = {\pi e^{-b} \over 2b} .\end{align*}
Linear or sublinear decay
\begin{align*} I = \int_{\mathbf{R}}{x\sin(x) \over 1 + x^2}\,dx .\end{align*}
Write \(f(z) = {ze^{iz} \over 1+z^2}\), and note that \(f\in { \mathsf{O}}\qty{1\over z}\), so the usual semicircular contour with the ML estimate won’t work. Claim: a semicircular contour with a better estimate will work:

Writing \(f(z) = e^{iz}g(z)\) where \(g(z) \coloneqq{z\over 1 + z^2}\), we have \(g\in { \mathsf{O}}\qty{1\over z} \to 0\) as \({\left\lvert {z} \right\rvert}\to \infty\), so Jordan’s lemma applies. Write \(C_1 = [-R, R]\) and \(C_R = \left\{{Re^{it} {~\mathrel{\Big\vert}~}t\in [0, \pi]}\right\}\), then \begin{align*} {\left\lvert {\int_{C_R} e^{iz} g(z)\,dz} \right\rvert}\leq \pi M_R,\, \qquad M_R \coloneqq\sup_{z\in C_R}{\left\lvert {z\over 1+z^2} \right\rvert} .\end{align*} Now use that \({z+1\over z^2}\leq M{\left\lvert {z} \right\rvert}\) for \({\left\lvert {z} \right\rvert}\) large enough to conclude this integral goes to zero. By the residue theorem, \begin{align*} 2\pi i \sum_{z_k\in {\mathbb{H}}}\mathop{\mathrm{Res}}_{z=z_k}f(z) = \int_{C_1 + C_R} f = \qty{\int_{C_1} + \int_{C_R}}f \overset{R\to\infty} \int_{C_1} f = I ,\end{align*} so it suffices to compute the residues of \(f\). Check that \(1+z^2 = (1+i)(1-i)\), so \(z_1 = i \in {\mathbb{H}}\) is a simple pole and \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=i} f(z) &= 2\pi i \lim_{z\to i} {e^{iz} \over z+i} \\ &= 2\pi i {i\over 2ei} = {\pi \over e} ,\end{align*} so \begin{align*} I = {\pi \over e} .\end{align*}
\begin{align*} I \coloneqq\int_{\mathbf{R}}{\cos(x) \over x+i}\,dx .\end{align*}
Note that the usual thing won’t work, since \({\cos(z) \over z+i}\neq \Re\qty{e^{iz}\over z+i};\) the complex constant in the denominator throws this off! Instead, use \(\cos(z) = {1\over 2}(e^{iz} + e^{-iz})\) to decompose into two integrals: \begin{align*} I \coloneqq\int_{\mathbf{R}}{\cos(z) \over z+i} = {1\over 2} \int_{\mathbf{R}}{e^{iz} \over z+i} + {1\over 2}\int_{\mathbf{R}}{e^{-iz} \over z+i} \coloneqq\int_{\mathbf{R}}f_1 + \int_{\mathbf{R}}f_2 ,\end{align*} These both have \(\deg(f_i) = -1\), so Jordan’s lemma on semicircular contours will work. For \(e^{i\alpha z}\), one needs to take the upper half-plane for \(\alpha>0\) (so \(f_1\)) and the lower for \(\alpha<0\) (for \(f_2\)). For \(f_1\), use the upper contour:

Then by Jordan’s lemma, since \(f(z) = e^{iz}g(z)\) with \(g(z) \to 0\) as \({\left\lvert {z} \right\rvert}\to \infty\), \(\int_{\gamma_R} f \to 0\) and we’re left with the residues in \({\mathbb{H}}\). Here, the only residue is at \(z=-i\), so this integral is zero. For \(f_2\), use the lower contour:
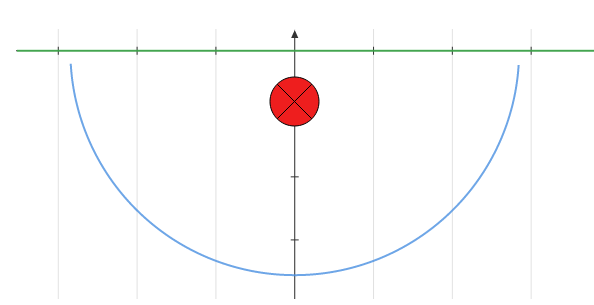
This is parameterized counterclockwise, and so the piece along \({\mathbf{R}}\) converges to \(-I\). By Jordan’s lemma \begin{align*} -I &= 2\pi i \mathop{\mathrm{Res}}_{z=-i} {e^{iz}\over 2(z+i)} \\ &= 2\pi i \lim_{z\to -i} {e^{iz}\over 2} \\ &= \pi i e^{-1} ,\end{align*} so \begin{align*} I = -{i\pi \over e} .\end{align*}
No clear decay
\begin{align*} I \coloneqq\int_{\mathbf{R}}{e^{x\over 2}\over 1+e^x}\,dx .\end{align*}
Replication: find \(b\) such that \(f(z) = f(z+ib)\) and use a rectangle. \begin{align*} f(z+ib) = {e^{z\over 2}e^{ib\over 2} \over 1 + e^{ib}e^z} = e^{ib\over 2} {e^{z\over 2} \over 1 + e^{ib}e^z } = f(z) \impliedby e^{ib} = 1 \impliedby b=2\pi ,\end{align*} in which case \begin{align*} f(z + 2\pi i) = e^{ib\over 2}f(z) = e^{2\pi i \over 2}f(z) = -f(z) .\end{align*}
So take the following rectangle where \(H_-\) is at \(2\pi i\) and \(H_+\) is at 0, with sides at \(\pm R\):
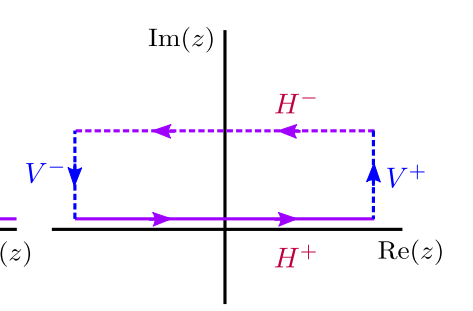
Write \(\Gamma\) for the entire contour. Note that integrating left-to-right on \(H_-\) yields \(-I\), since \(w = z+2\pi i\) for \(w\in H_-\) and \(f(w) = -f(z)\). Then reversing the orientation, going right-to-left yields \(\int_{H_i} f = I\).
Claim: the integrals over the sides \(V_{\pm}\) vanish. For the right, \begin{align*} {\left\lvert {\int_{V_+} f(z) \,dz} \right\rvert} &\leq 2\pi \sup_{t\in [0, 2\pi]} {\left\lvert {e^{R + it\over 2} \over 1 + e^{R + it} } \right\rvert} \\ &\leq 2\pi \sup_t {{\left\lvert { e^{R\over 2} e^{it \over 2} } \right\rvert} \over {\left\lvert {e^{R}e^{it}} \right\rvert} - 1} \\ &\leq 2\pi \sup_t {{\left\lvert { e^{R\over 2} } \right\rvert} \over {\left\lvert {e^{R}} \right\rvert} - 1} \\ &\in { \mathsf{O}}(e^{- {R\over 2} }) \to 0 .\end{align*}
For the left: \begin{align*} {\left\lvert {\int_{V_-} f(z) \,dz} \right\rvert} &\leq \sup_{t\in [0, 2\pi] } {\left\lvert { e^{-R-it\over 2} \over 1 + e^{-R- it}} \right\rvert} \\ &\leq \sup_{t\in [0, 2\pi]}{\left\lvert {e^{-R\over 2} e^{-it\over 2}} \right\rvert} \\ &\leq \sup_{t\in [0, 2\pi]}{\left\lvert {e^{-R\over 2}} \right\rvert} \\ &\in { \mathsf{O}}(e^{- {R\over 2} }) \to 0 ,\end{align*} where we’ve thrown away positive terms in the denominator, which only makes this quantity larger.
Finding the poles within \(\Gamma\): by inspection, there are poles when \(e^z=-1\), so at \(z=(2k+1)\pi i\) for \(k\in {\mathbf{Z}}\). Exactly one falls into this contour, \(z_k = i\pi\). By the residue theorem, \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=i\pi} f(z) = \int_\Gamma f(z) \,dz= \qty{\int_{H_-} + \int_{H_+}} f = 2I \implies I = \pi i \mathop{\mathrm{Res}}_{z=i\pi } f .\end{align*} Computing this residue: \begin{align*} \pi i \mathop{\mathrm{Res}}_{z=i\pi }f(z) &= \pi i \lim_{z\to i\pi} { (z-i\pi) e^{z\over 2}\over e^z + 1} \\ &{ \overset{\scriptscriptstyle\text{LH}}{=} }\pi i \lim_{z\to i\pi} {e^{z\over 2} \over e^z} \\ &= \pi i e^{-i\pi \over 2} \\ &= \pi .\end{align*}
DZG: This is much easier than trying to find the Laurent expansion about \(z=i\pi\) – trust me!
\begin{align*} I \coloneqq\int_{\mathbf{R}}{e^{ax} \over \cosh(x) }\,dx= \pi \sec\qty{a\pi \over 2} && {\left\lvert {\Re(a)} \right\rvert} < 1 .\end{align*}
Heuristically, \(\int e^{ax} { \mathrm{sech} }(x)\) should converge since \({ \mathrm{sech} }(x) \sim e^{-x}\), so \({\left\lvert {f} \right\rvert} \sim {\left\lvert {e^{(a-1)x}} \right\rvert}\sim e^{\Re(a-1)x} \sim e^{-x}\) when \(\Re(a-1)\) is negative, so \(\Re(a) < 1\).
We’ll need a contour along \({\mathbf{R}}\), so immediate options are a semicircular contour or a rectangle. A semicircular contour is not a good idea here, since there are infinitely many poles of this function: \begin{align*} \cosh(z) = 0 \implies e^z + e^{-z} = 0 \implies e^{2z} = -1 \implies z = {i\pi \cdot k \over 2} .\end{align*} It turns out the residues at these poles are all 1, the residue theorem would yield a divergent series. So take the rectangle contour with one side long \({\mathbf{R}}\) and one along \(\left\{{t+ib {~\mathrel{\Big\vert}~}t\in [-R, R]}\right\}\) respectively, where we’ll choose \(ib\) so that the two integrals differ by a scalar. Computing the symmetry by looking at \(f(z+ib)\): \begin{align*} {e^{a(z+ib)} \over \cosh(z+ib)} = e^{aib} {e^{z} \over e^z e^{ib} + e^{-z} e^{-ib} } ,\end{align*} and we now need \(e^{ib} = e^{-ib}\) in order to scale it out. Noting that if \(z\coloneqq e^{ib}\) then \(\overline{z} = e^{-ib}\), this forces \(z\in {\mathbf{R}}\), so \(z=\pm 1\). Taking \(z=+1\) forces \(b=0\), which is the original contour, so taking \(z=-1\) yields \(b=\pi i\). So we take the following contour:
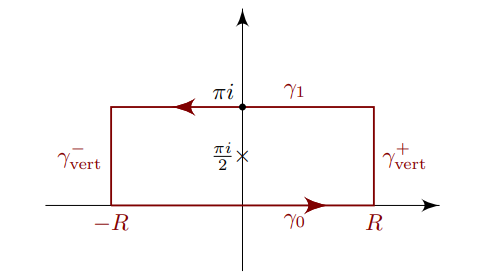
Computing the integral on the upper contour: \begin{align*} \int_{\gamma_1} f(z) \,dz &= \int_R^{-R} f(t+ib) \,dt\qquad z=t+ib, \,dz= \,dt\\ &= - \int_{-R}^R f(t+ib) \,dt\\ &= - \int_{-R}^R {e^{a(t+i\pi)} \over \cosh(t+i\pi ) } \,dt\\ &= - \int_{-R}^R e^{ai\pi} {e^{t} \over e^t e^{i\pi} + e^{-t} e^{-i\pi} } \,dt\\ &= - \int_{-R}^R e^{ai\pi} {e^{t} \over -e^t - e^{-t} } \,dt\\ &= \int_{-R}^R e^{ai\pi} {e^{t} \over e^t + e^{-t} } \,dt\\ &= e^{ai\pi} \int_{-R}^R {e^{t} \over e^t + e^{-t} } \,dt\\ &= e^{ai\pi} \int_{-R}^R {e^{t} \over \cosh(t) } \,dt\\ &= e^{ai\pi} \int_{\gamma_0} f(z) \,dz ,\end{align*} so \begin{align*} \qty{\int_{\gamma_0} + \int_{\gamma_1}} f = (1+e^{ai\pi}) I .\end{align*}
The integrals along the sides vanish as \(R\to\infty\).
The quick argument: \(\cos(z) \sim e^z\) so \({ \mathrm{sech} }(z) \sim e^{-z}\), so \begin{align*} {\left\lvert {f(R+ it)} \right\rvert} &= {\left\lvert {e^{a(R+it)}{ \mathrm{sech} }(R+it)} \right\rvert} \sim {\left\lvert { e^{aR}e^{-R}} \right\rvert} = {\left\lvert { e^{R(a-1)} } \right\rvert} = e^{R\cdot \Re(a-1)} \\ {\left\lvert {f(-R+ it)} \right\rvert} &= {\left\lvert {e^{a(-R+it)}{ \mathrm{sech} }(-R+it)} \right\rvert} \sim {\left\lvert { e^{-aR}e^{R}} \right\rvert} = {\left\lvert { e^{-R(a+1)}} \right\rvert} = e^{-R \cdot \Re(a+1)} ,\end{align*} where the first goes to zero when \(\Re(a)<1\) and the second when \(\Re(a) > -1\).
Parameterize the right contour as \begin{align*} \gamma^+ = \left\{{R+it {~\mathrel{\Big\vert}~}t\in [0, \pi]}\right\} .\end{align*} Then \begin{align*} {\left\lvert { \int_{\gamma^+} f(z) \,dz} \right\rvert} &= {\left\lvert { \int_0^\pi f(R+it) \,dt} \right\rvert} \qquad z=R+it, \,dz=\,dt\\ &= {\left\lvert { \int_0^\pi { e^{a(R+it)} \over \cosh(R+it) } \,dt} \right\rvert} \\ &= {\left\lvert { \int_0^\pi { e^{aR}e^{ait} \over e^Re^{it} + e^{-R} e^{-it} } \,dt} \right\rvert} \\ &\leq \int_0^\pi {\left\lvert {{ e^{aR}e^{ait} \over e^Re^{it} + e^{-R} e^{-it} } } \right\rvert} \,dt\\ &= \int_0^\pi {{ {\left\lvert { e^{aR}e^{ait} } \right\rvert} \over {\left\lvert { e^Re^{it} + e^{-R} e^{-it} } \right\rvert} } } \,dt\\ &\leq c\int_0^\pi {{ {\left\lvert { e^{aR} } \right\rvert} \over {\left\lvert { e^{-R} (e^{2R}e^{it} + e^{-it}) } \right\rvert} } } \,dt\qquad c\coloneqq e^{ait} \\ &= c\int_0^\pi {{ {\left\lvert { e^{(a-1)R} } \right\rvert} \over {\left\lvert {(e^{2R}e^{it} + e^{-it}) } \right\rvert} } } \,dt\\ &\leq c\int_0^\pi {{ {\left\lvert { e^{(a-1)R} } \right\rvert} \over {\left\lvert {e^{2R}e^{it} } \right\rvert} - {\left\lvert {e^{-it} } \right\rvert} } } \,dt\\ &= c\int_0^\pi {{ e^{\Re((a-1)R)} \over e^{2R} - 1 } } \,dt\\ &= {{ c\pi e^{\Re((a-1)R)} \over e^{2R} - 1 } } \\ &\leq {{ c\pi e^{R\cdot \Re((a-1))}} } \end{align*} which goes to zero provide \(\Re(a-1) < 0\), so \(\Re(a) < 1\) (as assumed). Here we’ve thrown out positive denominators, which only makes the terms larger.
Similarly, parameterized the left contour as \begin{align*} \gamma^- = \left\{{-R+it {~\mathrel{\Big\vert}~}t\in [0, \pi]}\right\} ,\end{align*} then \begin{align*} {\left\lvert { \int_{\gamma^-} f(z) \,dz} \right\rvert} &= {\left\lvert { \int_0^\pi f(-R+it) \,dt\qquad z=-R+it, \,dz=\,dt} \right\rvert} \\ &= {\left\lvert { \int_0^\pi { e^{a(-R+it)} \over \cosh(-R+it) } \,dt} \right\rvert} \\ &= {\left\lvert { \int_0^\pi { e^{-aR}e^{ait} \over e^{-R}e^{it} + e^{R} e^{-it} } \,dt} \right\rvert} \\ &\leq \int_0^\pi {\left\lvert {{ e^{-aR}e^{ait} \over e^{-R}e^{it} + e^{R} e^{-it} } } \right\rvert} \,dt\\ &= \int_0^\pi {{ {\left\lvert { e^{-aR}e^{ait} } \right\rvert} \over {\left\lvert { e^{-R}e^{it} + e^{R} e^{-it} } \right\rvert} } } \,dt\\ &\leq c\int_0^\pi {{ {\left\lvert { e^{-aR} } \right\rvert} \over {\left\lvert { e^{-R} (e^{it} + e^{2R}e^{-it}) } \right\rvert} } } \,dt\\ &= c\int_0^\pi {{ {\left\lvert { e^{-R(a+1)} } \right\rvert} \over {\left\lvert {(e^{it} + e^{2R}e^{-it}) } \right\rvert} } } \,dt\\ &\leq c\int_0^\pi {{ {\left\lvert { e^{-R(a+1)} } \right\rvert} \over {\left\lvert {e^{2R}e^{-it} } \right\rvert} - {\left\lvert {e^{it} } \right\rvert} } } \,dt\\ &= c\int_0^\pi {{ e^{\Re(-R(a+1))} \over e^{2R} - 1 } } \,dt\\ &= {{ c\pi e^{\Re(-R(a+1))} \over e^{2R} - 1 } } \\ &\leq {{ c\pi e^{-R \cdot \Re((a+1))}} } ,\end{align*} which now goes to zero provided \(\Re(a+1)>0\), so \(\Re(a) > -1\) (again as assumed).
Given thus, noting that only the pole \(z_0 = {i\pi \over 2}\) is enclosed, the residue theorem yields \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=z_0}f(z) = \int_\Gamma f = (1+e^{ai\pi})I \implies I = {2\pi i \mathop{\mathrm{Res}}_{z=z_0} f(z) \over 1 + e^{ai\pi}} .\end{align*} Computing the residue: \begin{align*} \mathop{\mathrm{Res}}_{z=z_0}f(z) &= \lim_{z\to z_0} {(z-z_0)e^{az} \over \cosh(z)}\\ &{ \overset{\scriptscriptstyle\text{LH}}{=} }\lim_{z\to z_0} {a(z-z_0) e^{az} \over \sinh(z)} + {e^{az}\over \sinh(z)} \\ &= {a \cdot 0 \cdot e^{ai\pi \over 2} \over i \sin\qty{\pi \over 2} } + {e^{a i \pi \over 2} \over i\sin\qty{\pi \over 2}} \\ &= {e^{ai\pi\over 2} \over i} \\ &= -i e^{ai\pi \over 2} ,\end{align*} where we’ve used that \(\sinh(iz) = i\sin(z)\). Putting it all together: \begin{align*} I &= {2\pi i \cdot -i e^{ai\pi \over 2} \over 1 + e^{a i \pi}} \\ &= {2\pi e^{ai\pi \over 2} \over 1 + e^{a i \pi}} \\ &= {2\pi \over e^{-ai\pi \over 2}\qty{ 1 + e^{a i \pi}} } \\ &= {2\pi \over e^{-ai\pi \over 2}+ e^{a i \pi\over 2} } \\ &= {\pi \over \cos\qty{a\pi \over 2}}\\ &= \pi \csc\qty{a\pi \over 2} .\end{align*}
Singularities along \({\mathbf{R}}\), Principal Values
Compute \begin{align*} I_1 \coloneqq\operatorname{PV}\int_{\mathbf{R}}{\sin(x) \over x}\,dx= \pi \\ I_2 \coloneqq\operatorname{PV}\int_{\mathbf{R}}{\cos(x) \over x}\,dx= 0 .\end{align*}
Take \(\Gamma\) an upper-half-plane semicircular contour indented at the origin; considering \(f(z) = e^{iz}\), by Jordan’s lemma \(\int_{C_R}f \to 0\) and the pieces along \({\mathbf{R}}\) converge to \({ \operatorname{PV} }\int f\). The singularity at \(z_0 = 0\) contributes a fractional residue: \begin{align*} \int_{C_{\varepsilon}}f(z)\,dz\to i\pi \mathop{\mathrm{Res}}_{z=z_0} f(z) = i\pi \lim_{z\to 0} {(z-0) e^{iz}\over z} = i\pi \cdot 1 .\end{align*} Thus \begin{align*} I \coloneqq{ \operatorname{PV} }\int_{\mathbf{R}}f(z)\,dz= 0 + i\pi \implies I_1 = \Im(I) = \pi, \quad I_2 = \Re(I) = 0 .\end{align*}
\begin{align*} I \coloneqq\int_{\mathbf{R}}{xe^{2ix} \over x^2-1}\,dx= i\pi \cos(2) .\end{align*}
Factor the denominator as \((z-1)(z+1)\), then there are two poles of order 1 on \({\mathbf{R}}\). Define a contour
- \(C_1: [-R, 1-{\varepsilon}_1]\)
- \(-C_2: -1 + Re^{it}, t \in [0, \pi]\)
- \(C_3: [1-{\varepsilon}, 1+{\varepsilon}]\)
- \(C_4: 1 + Re^{it}, t \in [0, \pi]\)
- \(C_R: Re^{it}, t\in [0, \pi]\)
- \(\Gamma = C_1 + \cdots + C_4 + C_R\)
So this, but with a semicircular contour instead of a rectangle:
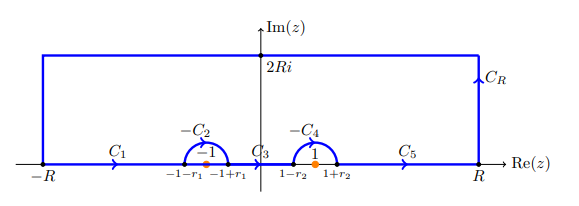
By Jordan’s lemma, \(\int_{C_R}\to 0\), and \(\qty{\int_{C_2} + \int_{C_3} + \int_{C_4}}\to 0\), while \(\int_\Gamma = 0\) since it encloses no singularities. Thus \begin{align*} 0 = \int_{C_2} f + \int_{C_4} f ,\end{align*} which converges to the fractional residues at \(z=\pm 1\).
For \(z=-1\), \begin{align*} \int_{C_2} &\to \pi i \mathop{\mathrm{Res}}_{z=-1} f(z) \\\ &= \pi i \lim_{z\to -1} {e^{2iz} \over z-1} \\ &= \pi i {e^{-2i} \over 2} .\end{align*}
For \(z=-1\): \begin{align*} \int_{C_4} &\to \pi i \mathop{\mathrm{Res}}_{z=1} f(z) \\\ &= \pi i \lim_{z\to 1} {e^{2iz} \over z+1} \\ &= \pi i {e^{2i} \over 2} .\end{align*}
Putting it all together: \begin{align*} I &= \pi i {e^{-2i} \over 2} + \pi i {e^{2i}\over 2} \\ &=\pi i \cos(2) .\end{align*}
Rational functions of \(\cos, \sin\)
\begin{align*} \int_{[-\pi, \pi]} {1\over 1 + \sin^2(\theta)} \,d\theta .\end{align*}
Set \(z=e^{i\theta}\), so \(\sin(\theta) = {z+z^{-1}\over 2i}\) and \(\sin^2(\theta) = -{1\over 4}(z^{-2}-2+z^2)\). Then \begin{align*} I\coloneqq\int_{[-\pi, \pi]} {1\over 1 + \sin^2(\theta)} \,d\theta &= \int_{S^1} {1\over 1 - {1\over 4}(z^{-2} -2 + z^2) } {1\over iz}\,dz\\ &= \int_{S^1} {-4i \over z(4-(z^{-2} -2 + z^2))}\,dz\\ &= \int_{S^1} {-4iz \over z^2(6-z^{-2} - z^2)}\,dz\\ &= \int_{S^1} {4iz \over z^4-6z^2+1}\,dz\\ &= 2\pi i \sum_{z_k\in {\mathbb{D}}} \mathop{\mathrm{Res}}_{z=z_k} {4iz\over z^4-6z^2+1} .\end{align*}
Factoring the denominator: \begin{align*} w^2 - 6w - 1 =0 &\implies w^2 - 6w + \qty{-6\over 2}^2 - \qty{-6\over 2}^2 + 1 =0 \\ &\implies (w - 3)^2 = -1 + 9 = 8 \\ &\implies w-3 = \zeta_2^k \sqrt{8},\, k=0, 1 \\ &\implies w = 3 \pm \sqrt{8} \\ &\implies z= \pm\sqrt{3\pm \sqrt 8} .\end{align*} Write these roots as
- \(z_1 \coloneqq\sqrt{3-\sqrt 8}\)
- \(z_2 \coloneqq-\sqrt{3-\sqrt 8}\)
- \(z_3 \coloneqq\sqrt{3+\sqrt 8}\)
- \(z_4 \coloneqq-\sqrt{3 + \sqrt 8}\)
Some numerology to figure out the modulus of these roots:
- \(3 + \sqrt{8} = 3+2\sqrt{2} 3+2\cdot(1.4) \approx 5.8\), so \({\left\lvert { \pm \sqrt{3+\sqrt 8}} \right\rvert}>\sqrt{4}>2>1\).
- \(3-\sqrt{8} \approx 3-2.8 \approx 0.2\) so \({\left\lvert { \pm \sqrt{3-\sqrt 8} } \right\rvert} < 1\).
So it suffices to compute the residues at \(z_1, z_2 = \pm \sqrt{3-\sqrt 8}\): At \(z_1\): \begin{align*} \mathop{\mathrm{Res}}_{z = z_1} &= \lim_{z\to z_1} {(z-z_1) 4i z \over z^4-6z^2+1 } \\ &\overset{\text{LH}}{=} \lim_{z\to z_1} { 4iz + 4i(z-z_1) \over 4z^3 -12z} \\ &= {4iz_1 \over 4z_1^3 - 12z_1} \\ &= {i\over z_1^2 - 3} \\ &= {i\over (3-\sqrt 8) - 3} \\ &= -{i\over \sqrt 8} .\end{align*} At \(z_2\): \begin{align*} \mathop{\mathrm{Res}}_{z=z_2} &= \lim_{z\to z_2} {(z-z_2) 4i z \over z^4-6z^2+1 } \\ &= {4iz_2\over 4z_2^2 - 12z_2}\\ &= {i \over z_2^2 - 3} \\ &= -{i\over \sqrt 8} .\end{align*}
Thus \begin{align*} I = 2\pi i \cdot -{2i\over \sqrt 8} = {4\pi \over \sqrt{8}} .\end{align*}
\begin{align*} \int_{0}^{2 \pi} \frac{d \theta}{1+a^{2}-2 a \cos (\theta)} = \begin{cases}\frac{2 \pi}{a^{2}-1} & \text { if }|a|>1 \\ \frac{2 \pi}{1-a^{2}} & \text { if }|a|<1\end{cases} .\end{align*}
The usual substitution: \(z=e^{i\theta}, \,dz= (iz)\,d\theta\). \begin{align*} I\coloneqq\int_{[0, 2\pi]} \qty{a^2 - 2a\cos(\theta) + 1}^{-1}\,d\theta &= \oint \qty{a^2-2(z+z^{-1}) + 1}^{-1}(iz)^{-1}\,dz\\ &= -i\oint \qty{za^2 - a(z^2+1) +z}^{-1}\,dz\\ &= -i \oint\qty{-az^2 + (a^2+1)z - a}^{-1}\,dz\\ &= {i\over a}\oint \qty{z^2 - \qty{a^2+a\over a}z + 1}^{-1}\,dz\\ &= {i\over a}\oint (z-a)^{-1}(z-a^{-1})^{-1}\,dz ,\end{align*} noting that \({a^2+a\over a} = a+a^{-1}\). Now there are two cases:
-
\({\left\lvert {a} \right\rvert} < 1\): then \(a\in {\mathbb{D}},a^{-1}\in {\mathbb{D}}^c\), so there is a simple pole at \(a\). Then \begin{align*} I &= {i\over a}\, 2\pi i \mathop{\mathrm{Res}}_{z=a} (z-a)^{-1}(z-a^{-1})^{-1}\\ &= -{2\pi \over a} (z-a^{-1})^{-1}\Big|_{z=a} \\ &= -{2\pi \over a(a-a^{-1})} \\ &= {2\pi \over 1 - a^2} .\end{align*}
-
\({\left\lvert {a} \right\rvert}> 1\): then \(a^{-1}\in {\mathbb{D}}, a\in {\mathbb{D}}^c\) so there is a simple pole at \(a^{-1}\). Then \begin{align*} I &= {i\over a}\, 2\pi i \mathop{\mathrm{Res}}_{z=a^{-1}} (z-a)^{-1}(z-a^{-1})^{-1}\\ &= -{2\pi \over a} (z-a)^{-1}\Big|_{z=a^{-1}} \\ &= -{2\pi \over a(a^{-1}- a)} \\ &= {2\pi \over a^2 - 1} .\end{align*}
\begin{align*} \int_{0}^{2 \pi} \frac{d \theta}{a+b \cos \theta}=\frac{2 \pi}{\sqrt{a^{2}-b^{2}}} .\end{align*}
The usual substitution: \(z=e^{i\theta}, \,d\theta= (iz)^{-1}\,dz\). \begin{align*} \int_{[0, 2\pi]} (a +b\cos(\theta))^{-1}\,d\theta &= \oint \qty{ a + {b\over 2}(z+z^{-1})}^{-1}(iz)^{-1}\,dz\\ &= -i\oint \qty{ za + {b\over 2}(z^2 + 1)} ^{-1}\,dz\\ &= -i \oint \qty{{b\over 2}z^2 + az + {b\over 2} }^{-1}\,dz\\ &= -{2i\over b} \oint \qty{z^2 + {2a\over b}z + 1}^{-1}\,dz\\ &= -{2i\over b}\oint (z-r_1)^{-1}(z-r_2)^{-1}\,dz ,\end{align*} where the roots can just be found using the quadratic formula \begin{align*} z_k &= {1\over 2} \qty{-{2a\over b} \pm \sqrt{\qty{2a\over b}^2 - 4}} \\ &= -{a\over b}\pm {1\over 2}\sqrt{{4a^2 \over b^2} - 4} \\ &= -{a\over b}\pm \sqrt{{a^2 \over b^2} - 1} \\ &= -{a\over b}\pm \sqrt{{a^2 - b^2 \over b^2}} \\ &= -{a\over b}\pm {1\over b } \sqrt{{a^2 - b^2}} .\end{align*} Thus \begin{align*} r_1 &\coloneqq b^{-1}\qty{-a + \sqrt{a^2-b^2}} \\ r_2 &\coloneqq b^{-1}\qty{-a - \sqrt{a^2-b^2}} .\end{align*}
Since \(r_1 r_2 = 1\) and thus \({\left\lvert {r_1 r_2} \right\rvert} = 1\), only one root is in \({\mathbb{D}}\) and this yields one simple pole. Assume \(a>b\). Note that for \(r_2\), \({\left\lvert {a/b} \right\rvert} > 1\) and \({\left\lvert {a^2-b^2} \right\rvert}>0\), so \(r_2 \approx -1 - {\varepsilon}< -1\), so \(r_1\in {\mathbb{D}}\). Computing the residue here: \begin{align*} \mathop{\mathrm{Res}}_{z=r_1} (z-r_1)^{-1}(z-r_2)^{-1} &= (z-r_2)^{-1}\Big|_{z=r_1} \\ &= (r_1 - r_2)^{-1}\\ &= \qty{2b^{-1}\sqrt{a^2-b^2} }^{-1} ,\end{align*} so \begin{align*} I &= 2\pi i \cdot -{2 i \over b}{b\over 2\sqrt{a^2-b^2}} \\ &= {2\pi \over \sqrt{a^2-b^2} } .\end{align*}
Branch Cuts
Logarithms
\begin{align*} I \coloneqq\int_0^\infty {\log(x) \over 1+x^2}\,dx= 0 .\end{align*}
Noting the partial \(\zeta_2 = -1\) symmetry, take a branch cut for \(\log\) along \(\theta = -\pi/2\) and the following semicircular contour:
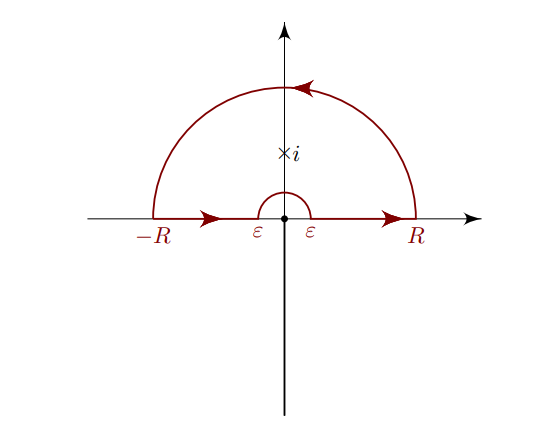
Since \(f(z) \coloneqq{\log(z) \over z^2 + 1}\) goes to zero as \({\left\lvert {R} \right\rvert}\to \infty\) and \({\varepsilon}\to 0\), only the horizontal contours will contribute. Parameterize, oriented counterclockwise:
- \(\gamma_1 \coloneqq\left\{{t+0i {~\mathrel{\Big\vert}~}t\in [{\varepsilon}, R]}\right\}\)
- \(\gamma_2 \coloneqq\left\{{t+0i {~\mathrel{\Big\vert}~}t\in [-{\varepsilon}, -R]}\right\}\)
Then \(\int_{\gamma_1} f(z)\,dz\to I\). Computing the contribution from \(\gamma_2\): \begin{align*} \int_{\gamma_2} f(z) \,dz &= \int_{-R}^{-{\varepsilon}} f(t) \,dt\qquad z=t+0i, \,dz=\,dt\\ &= \int_{-R}^{-{\varepsilon}} {\log(t) \over t^2 + 1}\,dt\\ &= -\int_{R}^{{\varepsilon}} {\log(-x) \over (-x)^2 + 1 }\,dx\qquad t=-x, \,dt= -\,dx\\ &= \int_{{\varepsilon}}^{R} {\log(x) + i\pi \over x^2 + 1 }\,dx\\ &= I + i\pi \cdot {\pi \over 2} \\ &= I + {i\pi^2\over 2} ,\end{align*} using the known antiderivative \(\arctan\).
Note that there are two simple poles at \(\pm i\), so only the residue at \(z_0=i\) contributes: \begin{align*} \mathop{\mathrm{Res}}_{z=i} = \lim_{z\to i} {\log(z) \over (z+i)} = {\log(i) \over 2i} = {i\pi/2 \over 2i} = {\pi \over 4} ,\end{align*} so by the residue theorem, \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=i}f(z) = \int_{\Gamma}f(z) \,dz= \qty{ \int_{\gamma_1} + \int{\gamma_2}}f = 2I + {i\pi^2 \over 2} \\ \implies 2\pi i \cdot {\pi \over 4} = I + {i\pi^2\over 2} \\ \implies {i\pi^2\over 4} = I + {i\pi^2\over 4} \\ \implies I = 0 .\end{align*}
\begin{align*} I\coloneqq\int_0^\infty {\log(x) \over (1+x^2)^2}\,dx= -{\pi \over 4} .\end{align*}
Let \(f\) be the integrand, then \(f\sim \log(z)/(z^4+1)\), so an indented semicircular contour will work since \({\left\lvert {f} \right\rvert}\to 0\) as \({\left\lvert {z\to\infty} \right\rvert}\), and the inner integral will be dominated by a term of the form \({\varepsilon}\log({\varepsilon})/{\varepsilon}^4\to 0\) as \({\varepsilon}\to 0\). So take such a contour, branch cutting along \(\theta = -\pi/2\):

Now consider the contribution from \(\gamma_2\): \begin{align*} \int_{\gamma_2} f(z) \,dz &= \int_{-R}^{-{\varepsilon}} f(t+0i) \,dt\\ &= \int_{-R}^{-{\varepsilon}} {\log(t) \over (t^2 + 1)^2 }\,dt\\ &= -\int_{R}^{{\varepsilon}} {\log(-x) \over ((-x)^2 + 1)^2 }\,dx\\ &= \int_{{\varepsilon}}^{R} {\ln{\left\lvert {x} \right\rvert} + i\pi \over (x^2 + 1)^2 }\,dx\\ &\to I + i\pi \int_{0}^\infty {1\over (x^2 + 1)^2}\,dx .\end{align*} This auxiliary integral can be handled easily with a usual semicircular contour, since the integrand is \({ \mathsf{O}}(x^4)\): \begin{align*} \int_{0}^\infty {1\over (z^2 + 1)}\,dx &= 2\pi i \sum_{z_k\in {\mathbb{H}}}\mathop{\mathrm{Res}}_{z=z_k} {1\over (z^2 + 1)} \\ &= 2\pi i \mathop{\mathrm{Res}}_{z=i} {1\over (z^2 + 1)} \\ &= 2\pi i \lim_{z\to i} {\frac{\partial }{\partial z}\,} {1\over (z+i)^2} \\ &= 2\pi i \cdot {-2\over (2i)^3 } \\ &= 2\pi i \cdot {-i\over 4} \\ &= {\pi \over 2} .\end{align*} Computing the residue of the main integral: \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=i} f(z) &= 2\pi i \lim_{z\to i} {\frac{\partial }{\partial z}\,} { \log(z) \over (z+i)^2} \\ &= 2\pi i \lim_{z\to i} { (z+i)^2 z^{-1}- 2(z+i)\log(z) \over (z+i)^4 } \\ &= 2\pi i { -i(2i)^2 - 2(2i)\qty{i\pi \over 2} \over (2i)^4 } \\ &= \pi i { 2i + \pi \over 2^2 }\\ &= -{\pi \over 2} + {i\pi^2 \over 4} .\end{align*} Combining all of this: \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=i} f(z) = \int_\Gamma f(z) \,dz= \qty{\int_{\gamma_1} + \int_{ \gamma_2} } f = I + \qty{I + {i\pi^2\over 4}} \\ \implies -{\pi \over 2} + {i\pi^2 \over 4} = 2I + {i\pi^2\over 4} \\ \implies -{\pi\over 2} = 2I \\ implies I = -{\pi \over 4} .\end{align*}
Factor \((1+z^2)^2 = (z+i)^2(z-i)^2\). Apropos of nothing, considering the auxiliary function \begin{align*} g(z) \coloneqq\qty{\log(z) \over 1+x^2}^2 = {\log^2(z) \over (1+x^2)^2} .\end{align*} Use a keyhole contour for a branch cut along \(\theta = -\pi\), so \(\operatorname{Arg}(z) \in (-\pi, \pi)\):
- \(\gamma_+: \left\{{t + i{\varepsilon}{~\mathrel{\Big\vert}~}t \in [-{\varepsilon}, -R]}\right\}\),
- \(\gamma_{{\varepsilon}}: \left\{{{\varepsilon}e^{it} {~\mathrel{\Big\vert}~}t\in [-\pi + {\varepsilon}, \pi - {\varepsilon}] }\right\}\),
- \(\gamma_+: \left\{{t - i{\varepsilon}{~\mathrel{\Big\vert}~}t \in [-{\varepsilon}, -R]}\right\}\),
- \(\gamma_{R}: \left\{{R e^{it} {~\mathrel{\Big\vert}~}t\in [-\pi + {\varepsilon}, \pi - {\varepsilon}] }\right\}\),
and \(\Gamma\) the combined contour oriented counterclockwise. Note the symmetry: \begin{align*} \int_{\gamma_+}g(z) &= \int_{-R}^{-{\varepsilon}} { \log^2(t) \over (t^2 +1)^2 } \,dt\\ &= - \int_{-eps}^{-R} { \log^2(t) \over (t^2 +1)^2 } \,dt\\ &= \int_{{\varepsilon}}^{R} { \log^2(e^{i\pi} s) \over ( ( e^{i\pi} s)^2 +1)^2 } \,ds&& t = e^{i\pi}s,\, \,ds= -\,dt\\ &= \int_{{\varepsilon}}^{R} { \qty{ \log(s) + i\pi}^2 \over (s^2 +1)^2 } \,ds\\ ,\end{align*} and similarly \begin{align*} \int_{\gamma_-}g(z) &= \int_{-{\varepsilon}}^{-R} { \log^2(t) \over (t^2 +1)^2 } \,dt\\ &= -\int_{{\varepsilon}}^{R} { \log^2(e^{-i\pi} s) \over ((e^{-i\pi} s)^2 +1)^2 } \,ds&& t=e^{-i\pi }s,\, \,dt= -\,ds\\ &= -\int_{{\varepsilon}}^{R} { \qty{ \log(s) - i\pi}^2 \over (s^2 +1)^2 } \,dt\\ .\end{align*} Now note that \begin{align*} (\log(s) + i\pi)^2 - (\log(s) - i\pi)^2 &= \cdots \\ &= \qty{\log^2(s) + 2i\pi \log(s) - \pi^2 } - \qty{\log^2(s) -2i\pi\log(s) - \pi^2} \\ &= 4i\pi\log(s) ,\end{align*} and so miraculously \begin{align*} \int_{\gamma_+}f(z)\,dz+ \int_{\gamma_-}f(z)\,dz &= \int_{{\varepsilon}}^{R} { \qty{ \log(s) + i\pi}^2 \over (s^2 +1)^2 } \,ds- \int_{{\varepsilon}}^{R} { \qty{ \log(s) - i\pi}^2 \over (s^2 +1)^2 } \,dt\\ &= \int_{\varepsilon}^R { \qty{ \log(s) + i\pi}^2 - \qty{ \log(s) - i\pi}^2 \over (s^2+1)^2 }\,ds\\ &= 4i\pi \int_{{\varepsilon}}^R {\log(s) \over (s^2+1)^2}\,ds\\ &\longrightarrow 4i \pi I .\end{align*} The contributions from \(\gamma_R\) vanish since \({\log(z) \over z^4}\to 0\) as \({\left\lvert {z} \right\rvert}\to \infty\), and the contribution from \(\gamma_{\varepsilon}\) vanish since \({{\varepsilon}\log({\varepsilon}) \over {\varepsilon}^4+c}\to 0\) as \({\varepsilon}\to 0\) (and applying the ML estimate). Thus \begin{align*} 2\pi i \sum_{z_k\in {\mathbf{C}}}\mathop{\mathrm{Res}}_{z=z_k}g(z) = \int_\Gamma g(z) \,dz= 4i\pi I .\end{align*} Factoring the denominator as \((1+z^2)^2 = (z-i)^2(z+i)^2\), there are two order 2 poles at \(\pm i\). At \(z=i\): \begin{align*} \mathop{\mathrm{Res}}_{z=i}g(z) &= \lim_{z\to i} {\frac{\partial }{\partial z}\,} {\log^2(z) \over (z+i)^2} \\ &= \lim_{z\to i} {(z+i)^2 2\log(z)z^{-1}- \log^2(z) 2(z+i) \over (z+i)^4} \\ &= 2^{-4}\qty{(2i)^2 \cdot 2 \cdot {i\pi \over 2} {1\over i} - \qty{i\pi \over 2}^2 \cdot 2 \cdot 2i} \\ &= 2^{-4}\qty{2^3 i^2 {\pi \over 2} - 2^{-2}i^2 \pi^2 2^2 i} \\ &= 2^{-4}\qty{-2^2\pi + i\pi ^2} \\ &= r_1 \coloneqq- {\pi \over 4} + i {\pi^2\over 16} .\end{align*} Similarly, \begin{align*} \mathop{\mathrm{Res}}_{z=-i}g(z) &= \lim_{z\to -i} {\frac{\partial }{\partial z}\,} {\log^2(z) \over (z+i)^2} \\ &= \lim_{z\to -i} {(z-i)^2 2\log(z) z^{-1}- \log^2(z) 2(z-i) \over (z-i)^4} \\ &= 2^{-4} \qty{ (-2i)^2 \cdot 2 \qty{-i\pi \over 2}{1\over -i} - \qty{-i\pi\over 2}^2 \cdot 2(-2i) } \\ &= 2^{-4} \qty{ 2^2 i^2 \pi - 2^{-2} \pi^2 (-4i) }\\ &= 2^{-4}\qty{-2^2\pi - \pi^2} \\ &= r_2 \coloneqq-{\pi \over 4} - i {\pi^2\over 16} .\end{align*} Solving for \(I\) above, we have \begin{align*} I &= {2\pi i \over 4\pi i}(r_1 + r_2) \\ &= {1\over 2} \qty{- {\pi \over 4} - {\pi \over 4}} \\ &= -{\pi \over 4} .\end{align*}
\begin{align*} \int_0^\infty {\log(x) \over x^2+a^2}\,dx&= {\pi\log(a)\over 2a} && a>0 .\end{align*}
Note that the poles are at \(z=\pm ia\), and since \(\lim_{{\left\lvert {z} \right\rvert}\to\infty}f(z) = 0\) and \(\lim{R\to 0} {R\log(R)\over R^2 + a^2} = 0\), an indented semicircular contour will work.
Computing the contribution from the residues: \begin{align*} \mathop{\mathrm{Res}}_{z=ia}f(z) &= \lim_{z\to ia }{\log(z) \over (z+ia)} \\ &= {\log(ia) \over 2ia} \\ &= {\log(a) + i\pi/2 \over 2ia} \\ &= {\pi \over 4a} + {\log(a) \over 2ia} \\ \\ \implies 2\pi i \mathop{\mathrm{Res}}_{z=ia}f(z) &= {i\pi^2 \over 2a} + {\pi\log(a) \over a} .\end{align*} The contribution from the integrals will come from \(\qty{\int_{\gamma_1} + \int_{\gamma_2}}f\) where
- \(\gamma_1 \coloneqq\left\{{tR + (1-t){\varepsilon}{~\mathrel{\Big\vert}~}t\in [{\varepsilon}, R] }\right\}\)
- \(\gamma_2 \coloneqq\left\{{t(-{\varepsilon}) + (1-t)(-R) {~\mathrel{\Big\vert}~}t\in [{\varepsilon}, R] }\right\}\),
so that the overall contour is oriented counterclockwise. Noting that \(\int_{\gamma_1}f(z)\,dz\to I\) the desired integral, the other contribution is \begin{align*} \int_{\gamma_2}f(z)\,dz &= \int_{-R}^{-{\varepsilon}} {\log(t)\over t^2 + a^2}\,dt\\ &= - \int_{-{\varepsilon}}^{-R} {\log(t) \over t^2+a^2} \,dt\\ &= \int_{{\varepsilon}}^{R} {\log(-x) \over x^2+a^2} \,dt\qquad x=-t,\, \,dx= -\,dt\\ &= \int_{\varepsilon}^R {\log(x) \over x^2 + a^2}\,dx+ i\pi \int_{\varepsilon}^R {1\over x^2 +a^2}\,dx\\ &= I + i\pi\qty{\pi \over 2a} .\end{align*} In the limit, by the residue theorem we have \begin{align*} {i\pi^2 \over 2a} + {\pi\log(a) \over a} &= 2I + i\pi\qty{\pi \over 2a} \\ \implies I &= {\pi \log(a) \over 2a} .\end{align*}
\begin{align*} I\coloneqq\int_0^\infty {\log(x) \over 1+x^a}\,dx &= - \qty{\pi \over a}^2\cos\qty{\pi\over a}\csc^2\qty{\pi \over a} \\ &= - {\pi^2\over a^2} {\cos\qty{\pi\over a} \over \sin^2\qty{\pi\over a}} .\end{align*}
For the usual reasons, integrals along semicircles of radius \(R\) and \({\varepsilon}\) go to zero, so noting the poles at \(\omega_a \coloneqq e^{i\pi\over a}\), take an indented sector:
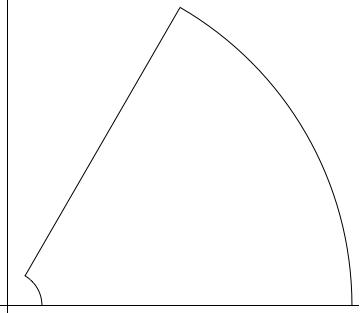
Set \(\zeta_a \coloneqq e^{2\pi i \over a}\). Contributions from the contours: let \(\gamma_1\) be the contour along \({\mathbf{R}}\) and \(\gamma_2\) along \(\zeta_a {\mathbf{R}}\), oriented so the overall contour is counterclockwise. Then \(\int_{\gamma_1}f(z)\,dz\to I\) for \(f(z) \coloneqq{\log(z) \over 1+z^a}\), so compute the monodromy term: parameterize \(\gamma_2 \coloneqq\left\{{\zeta_a t {~\mathrel{\Big\vert}~}t\in [{\varepsilon}, R]}\right\}\), so \begin{align*} \int_{\gamma_2}f(z) \,dz &=\int_R^{\varepsilon}f(\zeta_a t) \zeta_a \,dt\\ &= -\zeta_a \int_{\varepsilon}^R {\log(\zeta_a t) \over (\zeta_a t)^a + 1}\,dt\\ &= -\zeta_a \int_{{\varepsilon}}^R {\log(z) + {2\pi i \over a} \over t^a+1}\,dt\\ &\to -\zeta_a I - \zeta_a {2\pi i \over a} \int_0^\infty {1\over t^a + 1 }\,dt\\ &\coloneqq-\zeta_a I - {2\pi i\over a}\zeta_a I' .\end{align*}
\begin{align*} I' = {\pi\over a}\csc\qty{\pi\over a} .\end{align*}
Computing the auxiliary integral \(I'\): the integrand has the same pole at \(\omega_a\), so apply the same technique. Write \(g(z) \coloneqq{1\over z^a+1}\).
The contributions from the contours: \begin{align*} \qty{ \int_{\gamma_1} + \int_{\gamma_2}} g(z) \to (1-e^{2\pi i })I' = -2i\sin\qty{\pi\over a}e^{i\pi\over a} ,\end{align*} using the exponential balancing trick.
Computing the residue: \begin{align*} \mathop{\mathrm{Res}}_{z=e^{i\pi\over a}}g(z) &= {1\over az^{a-1}}\Big|_{z=e^{i\pi\over a}} = {1\over ae^{i\pi\qty{a-1\over a}}} = {1\over a e^{i\pi} e^{-i\pi\over a}} \\ \implies 2\pi i \mathop{\mathrm{Res}}_{z=e^{i\pi\over a}}g(z) &= -{2\pi i \over a}e^{i \pi \over a} .\end{align*}
Combining and solving: \begin{align*} I' = { - {2\pi i\over a} e^{i\pi \over a} \over -2i\sin\qty{\pi\over a}e^{i\pi\over a}} = {\pi \over a}\csc\qty{\pi \over a} .\end{align*}
Given this, the RHS of the residue theorem limits to \begin{align*} (1-\zeta_a) I - {2\pi i\over a}\zeta_a \qty{ {\pi \over a}\csc\qty{\pi\over a} } = (1-\zeta_a) I - {2\pi^2\over a^2}i\zeta_a \csc\qty{\pi\over a} .\end{align*}
For the LHS, we compute the residue at \(\omega_a\): \begin{align*} \mathop{\mathrm{Res}}_{z=\omega_a} f(z) &= \lim_{z\to \omega_a} {(z-\omega_a) \log(z) \over z^a + 1} \\ &{ \overset{\scriptscriptstyle\text{LH}}{=} }\lim_{z\to \omega_k} {\log(z) \over az^{a-1}}\\ &= {\log\qty{e^{i\pi \over a}} \over ae^{i\pi \qty{a-1\over a}} } \\ &= -{i\pi /a \over ae^{- i\pi \over a} } \\ &= -{i\pi \over a^2} e^{i\pi\over a} ,\end{align*} so \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=\omega_a} f(z) = -2\pi i \qty{i\pi\over a^2}e^{i\pi \over a} = {2\pi^2\over a^2}e^{i\pi\over a} .\end{align*}
After some truly arduous arithmetic, this assembles to: \begin{align*} {2\pi^2\over a^2}e^{i\pi\over a} &= (1-\zeta_a) I - {2\pi^2\over a^2}i\zeta_a \csc\qty{\pi\over a} \\ \\ \implies {2\pi^2\over a^2}e^{i\pi\over a} &= (1-e^{2\pi i\over a}) I - {2\pi^2\over a^2}ie^{2\pi i \over a} \csc\qty{\pi\over a} \\ \\ \implies {2\pi^2\over a^2} &= (e^{-{i\pi\over a}}-e^{\pi i\over a}) I - {2\pi^2\over a^2}ie^{\pi i \over a} \csc\qty{\pi\over a} \\ \\ &= -2i\sin\qty{\pi\over a}I - {2\pi^2\over a^2}ie^{\pi i \over a} \csc\qty{\pi\over a} \\ \\ \implies I &= { {2\pi^2\over a^2} + {2\pi^2\over a^2}ie^{\pi i \over a} \csc\qty{\pi\over a} \over -2i\sin\qty{\pi \over a} } \\\\ &= {2\pi^2\over a^2} \qty{ 1 + ie^{\pi i \over a} \csc\qty{\pi\over a} \over -2i\sin\qty{\pi \over a} } \\ \\ &= -{\pi^2\over a^2}\csc\qty{\pi\over a} \cdot (-i)\qty{1 + ie^{i\pi\over a}\csc\qty{\pi\over a}} \\ \\ &= -{\pi^2\over a^2}\csc\qty{\pi\over a} \qty{ -i + \qty{\cos\qty{\pi\over a} +i\sin\qty{\pi\over a}}\csc\qty{\pi\over a}} \\ \\ &= -{\pi^2\over a^2}\csc\qty{\pi\over a} \qty{-i + \cot\qty{\pi\over a} + i } \\ \\ &= -{\pi^2\over a^2}\csc\qty{\pi\over a} \cot\qty{\pi\over a} \\ &= -{\pi^2\over a^2}\cos\qty{\pi\over a} \csc^2\qty{\pi\over a} \\ .\end{align*}
Power Functions
\begin{align*} I \coloneqq\int_0^\infty {x^\alpha \over (x+1)^2}\,dx&& 0 < \alpha < 2 .\end{align*}
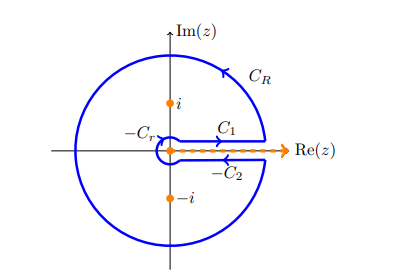
Note the single pole of order 2 at \(z=-1\), and also the branch singularity. Choose a branch cut of \(\log\) by deleting \(\theta=0\), and take a keyhole contour.
Write the contours as
- \(\gamma_{\varepsilon}= \left\{{{\varepsilon}e^{it} {~\mathrel{\Big\vert}~}t\in[0+{\varepsilon}, 2\pi - {\varepsilon}]}\right\}\)
- \(\gamma_+ = \left\{{x+i{\varepsilon}{~\mathrel{\Big\vert}~}x\in [{\varepsilon}, R]}\right\}\)
- \(\gamma_R = \left\{{Re^{it} {~\mathrel{\Big\vert}~}t\in [0+{\varepsilon}, 2\pi - {\varepsilon}]}\right\}\)
- \(\gamma_- = \left\{{x-i{\varepsilon}{~\mathrel{\Big\vert}~}t\in [{\varepsilon}, R]}\right\}\),
all oriented so that the total curve \(\Gamma\) is traversed counter-clockwise.
The claim is that \(\int_{\gamma_{\varepsilon}} f, \int_{\gamma_R} f\to 0\), and \(\int_{\gamma_+} f\) is a multiple of \(\int{\gamma_-} f\). For \(z=x-i{\varepsilon}\) on \(\gamma_-\), we have \begin{align*} \log(z) = \log(x-i{\varepsilon}) = \ln{\left\lvert {x-i{\varepsilon}} \right\rvert} + i\operatorname{Arg}(x-i{\varepsilon})\overset{{\varepsilon}\to 0}\longrightarrow \ln{\left\lvert {x} \right\rvert} + 2\pi i = e^{2\pi i}z ,\end{align*} and \begin{align*} f(e^{2\pi i}z) = {(e^{2\pi i}z)^\alpha \over ((e^{2\pi i}z)^2+1)^2 } = e^{2\pi i\alpha } {z \over z^2+1} = e^{2\pi i\alpha}f(z) .\end{align*} Thus \begin{align*} \int_{\gamma_-} f(z)\,dz &\longrightarrow\int_R^{\varepsilon}f(e^{2\pi i }z)\,dz\\ &= \int_R^{\varepsilon}e^{2\pi i \alpha}f(z)\,dz\\ &= -e^{2\pi i \alpha}\int_{\varepsilon}^R f(z)\,dz\\ &= -e^{2\pi i\alpha}\int_{\gamma_+}f(z)\,dz .\end{align*}
Thus in the limit, \begin{align*} 2\pi i \sum_{z_k\in {\mathbf{C}}\setminus{\mathbf{R}}_{\geq 0}} \mathop{\mathrm{Res}}_{z=z_k}f(z) &= \int_\Gamma f(z)\,dz\\ &= \int_{\gamma_+}f(z)\,dz+ \int_{\gamma_-}f(z)\,dz\\ &= (1-e^{2\pi i\alpha})\int_{\gamma_+}f(z)\,dz\\ &= (1-e^{2\pi i\alpha})\int_{{\mathbf{R}}}f(z)\,dz\\ .\end{align*}
Computing the residue at \(z_0 = -1\): \begin{align*} \mathop{\mathrm{Res}}_{z=-1}f(z) &= \lim_{z\to -1} {\frac{\partial }{\partial z}\,} (z+1)^2 f(z) \\ &= \lim_{z\to -1} {\frac{\partial }{\partial z}\,} z^\alpha \\ &= \alpha (-1)^{\alpha - 1} \\ &= \alpha e^{i\pi(\alpha - 1)} \\ &= -\alpha e^{i\pi \alpha} .\end{align*} Thus \begin{align*} \int_{\mathbf{R}}f(z) \,dz &= 2\pi i \cdot {-\alpha e^{i\pi \alpha}\over 1 - e^{2\pi i \alpha}} \\ &=-2\pi i \alpha {1\over e^{-i\pi\alpha} (1- e^{2\pi i \alpha})} \\ &=-2\pi i \alpha {1\over e^{-i\pi\alpha} - e^{i\pi\alpha}} \\ &=2\pi i \alpha {1\over e^{-i\pi\alpha} - e^{-i\pi\alpha}} \\ &= \pi \alpha \csc(\pi\alpha) .\end{align*}
\begin{align*} I\coloneqq\int_0^\infty {x^{1\over 3} \over 1 + x^2} \,dx= {\pi \over \sqrt 3} .\end{align*}
Write \(f(z) \coloneqq{z^{1\over 3}\over z^2+1}\), the claim is that an indented semicircular contour will work:

Why: after parameterizing \(C_R\), the integrand is approximately \(R\cdot R^{1\over 3}/ R^2 \sim R^{{4\over 3} - 2} = R{-{2\over 3}}\), which goes to zero as \(R\to \infty\). Similarly, on \(C_{\varepsilon}\), the integrand is approximately \({\varepsilon}^{4\over 3}/({\varepsilon}^2+1)\), which goes to zero as \({\varepsilon}\to 0\).
Note the poles at \(z=\pm i\). Computing the residue contribution at \(z=i\): \begin{align*} \mathop{\mathrm{Res}}_{z=i} f(z) &= {i^{1\over 3} \over 2i} = {1\over 2e^{i\pi \over 3}} .\end{align*}
Computing the contribution from the integrals: let \(\gamma_1\) be the contour along \({\mathbf{R}}_{\geq {\varepsilon}}\), and \(\gamma_2\) along \({\mathbf{R}}_{\leq {\varepsilon}}\). Noting that \(I = \int_{\gamma_1}f(z)\,dz\), \begin{align*} \int_{\gamma_2}f(z)\,dz &= \int_{-R}^{-{\varepsilon}} { t^{1\over 3} \over t^2 +1 } \,dt\\ &= -\int_R^{\varepsilon}{(-x)^{1\over 3} \over x^2+1}\,dx\qquad x=-t,\, \,dx= -\,dt\\ &= \int_{\varepsilon}^R {(\zeta_2 x)^{1\over 3} \over x^2+1}\,dx\\ &= \zeta_2^{1\over 3} I \\ &= e^{i\pi\over 3}I ,\end{align*} so \(\qty{\int_{\gamma_1} + \int_{\gamma_2}} f\) contributes \((1+e^{i\pi \over 3})I\). By the residue theorem, \begin{align*} 2\pi i \cdot {1\over 2e^{i\pi \over 3} } &= (1+e^{i\pi \over 3})I \\ \\ \implies I &= {i\pi \over 2e^{i\pi \over 3} (1+e^{i\pi \over 3}) } \\ &= {i\pi \over 2} \qty{ e^{i\pi \over 3} + e^{2i\pi \over 3} }^{-1}\\ &= {i\pi \over 2} \qty{ e^{i\omega} + e^{2i\omega} }^{-1},\qquad \omega={\pi\over 3} \\ &= {i\pi \over 2} \qty{ e^{3i\omega\over 2} \qty{ e^{-i\omega\over 2} + e^{i\omega\over 2}} }^{-1}\\ &= i\pi e^{-3i\omega\over 2}{1\over \cos\qty{\omega\over 2}} \\ &= i\pi e^{-i\pi\over 2 }{1\over \cos\qty{\pi \over 6}} \\ &= {\pi \over \sqrt{3}} ,\end{align*} where we’ve used the “exponential balancing trick” (see complex arithmetic section).
For the same reasons as in the semicircular solution, a keyhole will work:

The contributions from \(C_2\): \begin{align*} \int_{C_2}f(z) \,dz &= \int_R^{\varepsilon}{ (t-i{\varepsilon})^{1\over 3} \over (t-i{\varepsilon})^2 + 1 }\,dt\\ &= - \int^R_{\varepsilon}{ e^{{1\over 3}\qty{\ln{\left\lvert {t-i{\varepsilon}} \right\rvert} + i\operatorname{Arg}(t-i{\varepsilon}) } } \over (t-i{\varepsilon})^2 + 1 }\,dt\\ &\to - \int^R_{\varepsilon}{ e^{{1\over 3}\qty{\ln{\left\lvert {t} \right\rvert} + 2\pi i } } \over t^2 + 1 }\,dt\\ &= -\int_{\varepsilon}^R { e^{2\pi i \over 3} t^{1\over 3} \over t^2 + 1}\,dt\\ &= - \zeta_3 I ,\end{align*} so the contributions from the contours sums to \((1-\zeta_3 I)\).
The contributions from residues: \begin{align*} \mathop{\mathrm{Res}}_{z=\pm i} f(z) &= { (\pm i)^{1\over 3} \over \pm 2i} \cdot \\ &= { (e^{k\pi \over 2})^{1\over 3} \over \pm 2i},\qquad k=1,3\\ &= { e^{k\pi \over 6} \over \pm 2i} \\ &= \begin{cases} { e^{\pi\over 6} \over 2i} & z=i \\ {e^{3\pi \over 6} \over -2i} = -{1\over 2} & z=-i. \end{cases} .\end{align*} So the contribution from the residue theorem is \begin{align*} 2\pi i\qty{ {e^{\pi\over 6} \over 2i} - {i\over 2i} } = \pi\qty{e^{\pi\over 6} - 1} .\end{align*}
Solving for the integral: \begin{align*} I &= {\pi (e^{\pi \over 6} - i) \over 1 - e^{2i\pi \over 3}} \\ &=\pi { e^{i\omega} - e^{3i\omega} \over e^{0i\omega} - e^{4i\omega}},\qquad \omega = {\pi\over 6} \\ &= \pi {e^{2i\omega} \qty{e^{-i\omega} - e^{i\omega} } \over e^{2i\omega}\qty{e^{-2i\omega} - e^{2i\omega} } } \\ &= \pi {-2i\sin(\omega) \over -2i\sin(2\omega)} \\ &= \pi {\sin\qty{\pi\over 6} \over \sin\qty{\pi\over 3}} \\ &= \pi{ 1/2\over \sqrt{3}/2}\\ &= {\pi \over \sqrt 3} .\end{align*}
Square Roots / Slits
- The residue at \(\infty\): if \(\Gamma\) is a positively oriented curve (counterclockwise about \(z=0\)), then \begin{align*} \mathop{\mathrm{Res}}_{z=\infty}f(z) = -{1\over 2\pi i}\oint_\Gamma f(z) \,dz,\quad \mathop{\mathrm{Res}}_{z=\infty}f(z) = \mathop{\mathrm{Res}}_{z=0} -{1\over z^2}f\qty{1\over z} .\end{align*}
-
Slits: for \(f(z) = \sqrt{(z-z_1)(z-z_2)\cdots (z-z_n)}\), one needs to introduce slits that disallow winding around an odd number of the branch points \(z_k\).
- Be sure to check to see if \(z=\infty\) is a branch point!
- A standard argument: for \(f(z) = \sqrt{z}\), take a path \(\gamma(t) = e^{2\pi i t}\) for \(t\in [0, 1]\). Then \(f(\gamma(0)) = f(z)\) and \(f(\gamma(1)) = \sqrt{e^{2\pi i} z} = e^{i\pi}\sqrt{z} = -\sqrt{z}\), so the monodromy/phase factor introduced by square roots is \(-1\).
\begin{align*} I\coloneqq\int_{-1}^1 \sqrt{1-x^2} \,dx= {\pi \over 2} .\end{align*}
Take a branch cut \([-1, 1]\) and \(\Gamma\) the standard dogbone contour:
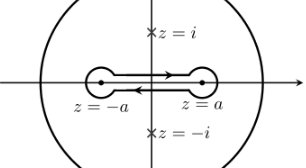
Orient \(\Gamma\) positively about infinity, i.e. counterclockwise.
Contribution from \(\gamma_1 \coloneqq\left\{{t+i{\varepsilon}{~\mathrel{\Big\vert}~}t\in [-1, 1]}\right\}\), the upper horizontal piece: \begin{align*} \int_{\gamma_1}f(z)\,dz\to \int_{-1}^1 \sqrt{1-t^2} \,dt= I .\end{align*}
Contribution from \(\gamma_2\coloneqq\left\{{t-i{\varepsilon}{~\mathrel{\Big\vert}~}t\in [-1, 1]}\right\}\), the lower horizontal piece: note that following \(e^{2\pi i t}z\) to \(t=1\) sends \(\sqrt{z}\) to \(-\sqrt{z}\), so \begin{align*} \int_{\gamma_2}f(z)\,dz\to \int_{1}^{-1} - \sqrt{1-t^2} \,dt= I .\end{align*}
Contributions from the circles: use that \(f(z) \coloneqq\sqrt{z^2-1}\) is a continuous function and these arcs are compact, so they are uniformly bounded. Thus \(\int f\to 0\) by the ML estimate on these arcs.
The total contribution: \begin{align*} \qty{\int_{\gamma_1} + \int_{\gamma_2}} f = 2I .\end{align*}
The residue at infinity: \begin{align*} \mathop{\mathrm{Res}}_{z=\infty}f(z) &= \mathop{\mathrm{Res}}_{z=0} - {1\over z^2}\sqrt{1 - {1\over z^2}} \\ &= \mathop{\mathrm{Res}}_{z=0} - {1\over z^2}\sqrt{z^2-1 \over z^2} \\ &= \mathop{\mathrm{Res}}_{z=0} - {i\over z^3}\sqrt{1-z^2} \\ &= \mathop{\mathrm{Res}}_{z=0} - {i\over z^3}\sum_{k\geq 0} {1/2\choose k}z^{2k} \\ &= \mathop{\mathrm{Res}}_{z=0} - {i\over z^3} \qty{1 - {1\over 2}z^2 - { \mathsf{O}}(z^3) } \\ &= {i\over 2} ,\end{align*} thus \begin{align*} 2\pi i \cdot -{i\over 2} = 2I \implies I = {\pi \over 2} .\end{align*}
\begin{align*} I \coloneqq\int_0^1 {1\over \sqrt{x^2-1}}\,dx= {i\pi \over 2} .\end{align*}
Write \(f(z) = \sqrt{z^2-1} = \sqrt{(z+1)(z-1)}\). First note \(f\) is even, so \begin{align*} I = {1\over 2}I',\qquad I' \coloneqq\int_{-1}^1 {1\over \sqrt{z^2-1}} \,dz .\end{align*}
Each branch point \(\pm 1\) introduces a monodromy factor of \(\sqrt{e^{2i\pi}} = e^{i\pi} = -1\), which cancel provided loops are not able to encircle a single branch point. So take the branch cut to be the slit \([-1, 1]\), forcing any loop to encircle neither or both of \(\pm 1\) – now use a dogbone contour \(\Gamma\) around the slit and apply the residue theorem to the exterior region:
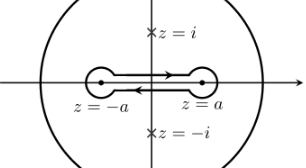
The contribution from the top segment \(\gamma_1\): \begin{align*} \int_{\gamma_1}f(z)\,dz\to \int_1^{-1} {1\over \sqrt{x^2-1}}\,dx= -I' .\end{align*} The contribution from the bottom segment \(\gamma_2\): a monodromy factor of \(-1\) is introduced to \(g(z)\coloneqq\sqrt{z}\) over a path that traces an angle of \(2\pi\), so \begin{align*} \int_{\gamma_2}f(z)\,dz= \int_{-1}^1 {1\over -\sqrt{x^2-1}} = -I' .\end{align*}
These combine to contribute \begin{align*} \qty{\int_{\gamma_1} + \int_{\gamma_2}}f = -2I' .\end{align*}
Note – we’ll want the contour to actually be positively oriented with respect to \(z=\infty\), so we should reverse the orientation of \(\Gamma\) to get a total contribution to \(2I\) instead.
The contribution from the small circles: parameterize the first as \(-1 + R e^{2\pi i t}\), then \begin{align*} {\left\lvert { \int_{C_{\varepsilon}^1}f(z)\,dz} \right\rvert} = {\left\lvert {\int_0^1 {2\pi i R e^{2\pi i t}\over \sqrt{ (-1 + R e^{2\pi i t} )^2 - 1 } } \,dt} \right\rvert} \sim \int_0^1 {R\over \sqrt{R^2-1}} \,dt\overset{R\to 0}\longrightarrow 0 .\end{align*} A similar bound works for the second circle using the parameterization \(1+ Re^{2\pi i t}\).
Contributions from residues: take the residue at infinity, \begin{align*} \mathop{\mathrm{Res}}_{z=\infty}f(z) &= \mathop{\mathrm{Res}}_{z=0}-{1\over z^2}f\qty{1\over z} \\ &= \mathop{\mathrm{Res}}_{z=0} {-1\over z^2\sqrt{z^{-2} - 1 }} \\ &= \mathop{\mathrm{Res}}_{z=0} {-1\over z\sqrt{1-z^2}} \\ &= \lim_{z\to 0} {-1\over \sqrt{1-z^2}}\\ &= -1 .\end{align*}
Putting this together \begin{align*} -2\pi i \mathop{\mathrm{Res}}_{z=\infty}f(z) &= \oint_\Gamma f(z)\,dz= 2I' \\ \implies 2\pi i &= 2I' \\ \implies \pi i &= I' = 2I \\ \implies I &= {i\pi \over 2} .\end{align*}
\begin{align*} I \coloneqq\int_{-1}^1 {1\over (x-a) \sqrt{1-x^2} }\,dx= {\pi \over \sqrt{a^2-1}} .\end{align*}
Note the simple pole at \(x=a\) and the branch points \(x=\pm 1\), coming from factoring \(\sqrt{1-z^2} = \sqrt{(1-z)(1+z)}\). The standard dog bone contour will work, but will involve a residue at \(z=a\) and at \(z=\infty\). Instead of taking the usual branch cut \([-1, 1]\), take instead \((-\infty, -1] \cup[1, \infty)\) and the following T-bone contour (noting that it is oriented negatively):
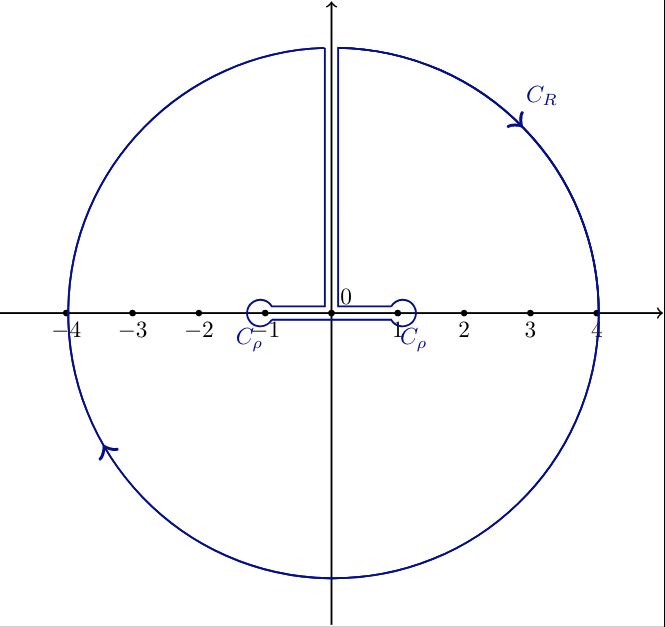
Note that in the limit, the two vertical pieces cancel since there is no phase introduced in \(f\) when taking a path from \(Q_1\) to \(Q_2\), and the two upper horizontal segment limit to \(\gamma_1\coloneqq\left\{{t+i{\varepsilon}{~\mathrel{\Big\vert}~}t\in[-1, 1]}\right\}\). Also note that \(\int_{\gamma_1}f(z)\,dz\to I\).
Let \(\gamma_2\) be the bottom horizontal segment. As in the arguments for the standard bone contour, \begin{align*} \int_{\gamma_2}f(z)\,dz= -\int_{\gamma_1} -f(z)\,dz= I ,\end{align*} so \begin{align*} \qty{\int_{\gamma_1} + \int_{\gamma_2} }f \to 2I .\end{align*}
The contribution from the residue: \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=a} {1\over (z-a) \sqrt{1-z^2} } = {2\pi i \over \sqrt{1-a^2}} = {2\pi \over \sqrt{a^2-1}} ,\end{align*} so \begin{align*} {2\pi \over \sqrt{a^2-1}} = 2I \implies I = {\pi \over \sqrt{a^2-1}} .\end{align*}
\begin{align*} \int_{1}^{\infty} \frac{d x}{x \sqrt{x^{2}-1}} = {\pi \over 2} .\end{align*}
Write \(f(z) \coloneqq(z^2-1)^{-{1\over 2}}/z\). In order for \((z^2-1)^{-{1\over 2}}\) to be well-defined, one needs to introduce a branch cut. Note that \(f\) has a simple pole at \(z=0\) and is holomorphic away from \(z=0\) if \(z^2-1\) is not on the positive real axis, where we’ve chosen the branch cut \(\theta = 0\) for \(\operatorname{Log}(z)\) and define \(z^{1\over 2} = e^{{1\over 2}\operatorname{Log}(z)}\). But \(z^2-1 \in {\mathbf{R}}_{\geq 0} \iff z\in [-1, 1]^c\), which is what we’ve cut.
So take the branch cut \((-\infty, 1] \cup[1, \infty)\) and use the following indented double-keyhole contour:

Contributions along \(C_8\) and \(C_6\): note that \(\int_{C_8}f \to I\), the desired integral. For reference, note that \(z^2-1 = (z+1)(z-1)\), and we can parameterize \begin{align*} C_8 = \left\{{t+1+ i{\varepsilon}{~\mathrel{\Big\vert}~}t\in [{\varepsilon}, R] }\right\} \implies \\ \int_{C_8}f(z)\,dz\to \int_0^\infty t^{-1}(t+2)^{-{1\over 2}} t^{-{1\over 2}} \,dt ,\end{align*} where on \(C_8\) we choose a branch of the square root so that \(\arg(z+1) \in [-\pi, \pi)\) and \(\arg(z-1)\in [-\pi, \pi)\). Now consider \(C_6\). Write \(\zeta_0 \coloneqq e^{2\pi i}\), then \begin{align*} C_6 = \left\{{\zeta_0 t + 1 - i{\varepsilon}{~\mathrel{\Big\vert}~}t\in [{\varepsilon}, R]}\right\} \implies \\ \int_{C_6} f(z)\,dz &\to \int_R^{{\varepsilon}} (\zeta_0 t)^{-1}(\zeta_0 t + 2)^{-{1\over 2}}(\zeta_0 t)^{-{1\over 2}}\,dt\\ &\to -\zeta_0^{-{3 \over 2}} \int_0^\infty t^{-1}(t+2)^{-{1\over 2}} t^{-{1\over 2}}\,dt\\ &= I ,\end{align*} since \(-\zeta_0^{-{3\over 2}} \coloneqq-e^{-3\pi i} = 1\). So in the limit \({\varepsilon}\to 0, R\to\infty\), \begin{align*} \qty{ \int_{C_8} + \int_{C_6}}f \longrightarrow 2I .\end{align*}
The contribution from \(C_2\): parameterize \begin{align*} C_2 = \left\{{s + i{\varepsilon}{~\mathrel{\Big\vert}~}x\in [-R, -1-{\varepsilon}]}\right\} ,\end{align*} which implies \begin{align*} \int_{C_2}f(z)\,dz &= \int_{-\infty}^{-1} {1\over s\sqrt{s^2-1}}\,ds\\ &= - \int_{\infty}^{1} {1\over (-x) \sqrt{(-x)^2-1}}\,dx,\qquad x=-s,\, \,dx= -\,ds\\ &= \int_\infty^1 {1\over (-x) \sqrt{ (-x)^2 - 1} }\,dx\\ &= - \int_\infty^1 {1\over x \sqrt{ x^2 - 1} }\,dx\\ &= \int_1^\infty {1\over x \sqrt{ x^2 - 1} }\,dx\\ &= I ,\end{align*} so the same argument as above shows \begin{align*} \qty{ \int_{C_2} + \int_{C_4}}f \longrightarrow 2I .\end{align*}
Computing the residues: the full contour encloses a simple pole at \(z=0\), so \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=0} f(z) = 2\pi i \lim_{z\to 0} {1\over \sqrt{z^2-1}} = 2\pi \cdot (-i) = 2\pi .\end{align*}
So by the residue theorem, \begin{align*} 2\pi = 2I + 2I \implies I = {\pi \over 2} .\end{align*}
\begin{align*} I\coloneqq\int_{\mathbf{R}}{1\over x^2 + 3x+ 2 }\,dx .\end{align*}
Note that \(f(x) = (x+2)(x+1)\), so the singularities on on \({\mathbf{R}}_{< 0}\). The function isn’t even, so a semicircular contour won’t work. Attempting to find a ray-like symmetry only yields one option: \begin{align*} f(z) = f(e^{i\theta } z) \implies \theta = 2k\pi ,\end{align*} which suggests a keyhole. But since there’s no \(\log\) in \(f\), there’s no monodromy, and the contributions cancel out. So introduce a log with a branch cut along \(\theta = 0\), and consider \begin{align*} \int f(z) \log(z) .\end{align*}
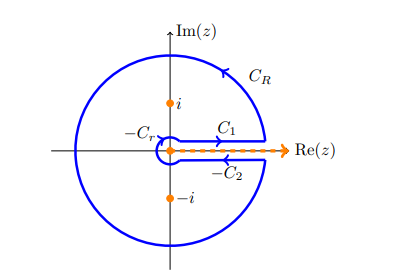
Let \(\gamma_+ = \left\{{t + i{\varepsilon}{~\mathrel{\Big\vert}~}t\geq 0}\right\}\) (right-to left) and \(\gamma_0 = \left\{{t-i{\varepsilon}{~\mathrel{\Big\vert}~}t\geq 0}\right\}\) (left-to-right). Now use the general fact \begin{align*} \int_{\gamma_+}f(z)\log(z) \,dz&= \int_{\varepsilon}^R f(t+i{\varepsilon})\log(t+i{\varepsilon}) \,dt\longrightarrow\int_{\mathbf{R}}f(t)\log(t)\,dt\\ \int_{\gamma_-}f(z)\log(z) \,dz&= \int_R^{\varepsilon}f(t-i{\varepsilon})\log(t-i{\varepsilon}) \,dt\longrightarrow-\int_{\mathbf{R}}f(t)\qty{ \log(t) + 2\pi i} \,dt\\ ,\end{align*} thus \begin{align*} \int_{\gamma_+}f(z)\log(z)\,dz+ \int_{\gamma_-}f(z)\log(z) &\longrightarrow\int_0^\infty f(t)\log(t)\,dt- \int_0^\infty f(t)(\log(t) + 2\pi i) \,dt\\ &= -2\pi i \int_0^\infty f(t) \,dt .\end{align*}
By the ML estimate, the semicircular piece vanishes. Miraculously, since \(\lim_{x\to 0}{ x\log(x) \over x^n+c} = 0\) for any \(c>0\) and \(n\geq 1\), the inner indented pieces goes to zero. Parameterize by \(z= {\varepsilon}e^{it}\) \begin{align*} \int_{C_{\varepsilon}} f(z)\log(z)\,dz &\approx \int_{{\varepsilon}}^{2\pi - {\varepsilon}} {\log({\varepsilon}e^{it}) \over {\varepsilon}^2 + 3{\varepsilon}+ 2} {\varepsilon}e^{it}\,dt\\ &= \int_{{\varepsilon}}^{2\pi - {\varepsilon}} {\log({\varepsilon}) + it \over {\varepsilon}^2 + 3{\varepsilon}+ 2} {\varepsilon}e^{it}\,dt\\ &\approx \int_{\varepsilon}^{2\pi - {\varepsilon}} {{\varepsilon}\log({\varepsilon}) + c_1 \over {\varepsilon}^2 + c_2}\,dt\\ &\overset{{\varepsilon}\to 0}\longrightarrow 0 ,\end{align*} where I’ve been extremely sloppy and left out many negligible \(e^{it}\) terms. By the residue theorem, \begin{align*} 2\pi i \sum_{z_k\in {\mathbf{C}}} \mathop{\mathrm{Res}}_{z=z_k} f(z)\log(z) = \int_\Gamma f(z)\log(z)\,dz= -2\pi i\int_{\mathbf{R}}f(z)\,dz .\end{align*} There are just two simple poles at \(z_1 = -1, z_2 = -2\), so For \(z_1\): \begin{align*} \mathop{\mathrm{Res}}_{z=-1}{\log(z) \over (z+1)(z+2)} = \lim_{z\to -1} {\log(z) \over z+2} = \log(-1) ,\end{align*} and for \(z_2\), \begin{align*} \mathop{\mathrm{Res}}_{z=-2}{\log(z) \over (z+1)(z+2)} = \lim_{z\to -2} {\log(z) \over z+1} = -\log(-2) .\end{align*}
Thus \begin{align*} I &= -(\log(-1) - \log(-2)) \\ &= - (\ln(1) + i\pi) + (\ln(2) + i\pi) \\ &= \ln(2) ,\end{align*} noting that we’ve chosen a branch of \(\log(z) \coloneqq\ln\qty{{\left\lvert {z} \right\rvert}} + i\operatorname{Arg}(z)\) where \(\operatorname{Arg}(z) \in (0, 2\pi)\).