See also [[30_Complex Analysis/999_Quals/105_Conformal Maps|Qual conformal map questions]].
Notation:
- Almost everything is an open set, so don’t include boundaries in definitions.
- \({\mathbb{D}}\coloneqq\left\{{z {~\mathrel{\Big\vert}~}{\left\lvert {z} \right\rvert} < 1}\right\}\) is the open unit disc.
- \({\mathbb{H}}\coloneqq\left\{{z {~\mathrel{\Big\vert}~}\Im(z) > 0}\right\}\) is the open upper half-plane.
- \(Q_i\) is the \(i\)th quadrant, e.g. \(Q_1 \coloneqq\left\{{z {~\mathrel{\Big\vert}~}\Re(z), \Im(z) > 0}\right\}\).
- \(Q_{ij} \coloneqq Q_i \cup Q_j\) is the union of two quadrants. E.g. \({\mathbb{H}}= Q_{23}\), or \(Q_{14}\) is the right half-plane.
Tips:
-
If just mapping the disc to itself, use the hypberolic translations \begin{align*} \psi_a \coloneqq{z-a\over 1-\overline{a} z} .\end{align*}
-
For lunes (regions bounded by arcs): map the cusps to \(0\) and \(\infty\) to get a sector.
-
For discs with slits: aim for \({\mathbf{C}}\setminus[0, \infty) \xrightarrow{\sqrt z} {\mathbb{H}}\).
-
For circles with tangencies: send the tangent point to \(\infty\) to get parallel lines.
-
Remembering the cross ratio: the order \(1,0,\infty\) is very important (as images of \(a, b, c\)).
- Send \(b\to 0\) by including \(z-b\) in the numerator.
- Send \(c\to \infty\) by including \(z-c\) in the denominator.
-
Send \(a\to 1\) by canceling the terms just added:
- Cancel \(z-c\) in the denominator with \(a - c\) in the numerator.
- Cancel \(z-b\) in the numerator with a \(a - b\) in the denominator.
-
Inverting conformal maps: just set \(f(z) = w\) and solve for \(w\).
-
Conformal maps preserve generalized spheres, i.e. circles get mapped to circles (which could be lines on \({\mathbf{CP}}^1\)).
-
Orthogonal circles must go to orthogonal circles.
-
Arcs between two points must go to arcs between their images
-
\({\mathbf{R}}=\left\{{\tan(t) {~\mathrel{\Big\vert}~}t\in (-\pi/2, \pi/ 2)}\right\}\).
Cross-Ratios
Use cross ratios: set \(T(z) \coloneqq(z;,1,i,2)\) and \(S(w) = (w;,3,0,-1)\) and solve \(T(z) = S(w) \implies w = (S^{-1}T)(z)\): \begin{align*} {z-i \over z-2}{1-2\over 1-i} &= {w-0\over w+1}{3+1 \over 3-0} \\ \implies -\frac{\left(i + 1\right) \, {\left(z - i\right)}}{2 \, {\left(z - 2\right)}} &= \frac{4 \, w}{3 \, {\left(w + 1\right)}} \\ \implies w &= -\frac{3 \, {\left(\left(i + 1\right) \, z - i + 1\right)}}{\left(3 i + 11\right) \, z - 3 i - 13} \\ &= - {3z - 3i \over {3i+11\over i+1}z + {-3i-13 \over 3i+11}} \\ &= - {3z - 3i \over (7-4i) z + {-8+5i} } \\ &= \frac{-3 z+3 i}{(7-4 i) z+(-8+5 i)} .\end{align*}
Find a conformal map from \({\mathbb{D}}^c \cap{\mathbb{H}}\) to \({\mathbb{H}}\) using cross-ratios.
Idea: all cross-ratios send the complement of a positively oriented region \((a,b,c)\) to the half-hemisphere \((1,0,\infty)\) on \({\mathbf{CP}}^1\). So take \((i, -1, 1)\to (1,0,\infty)\):
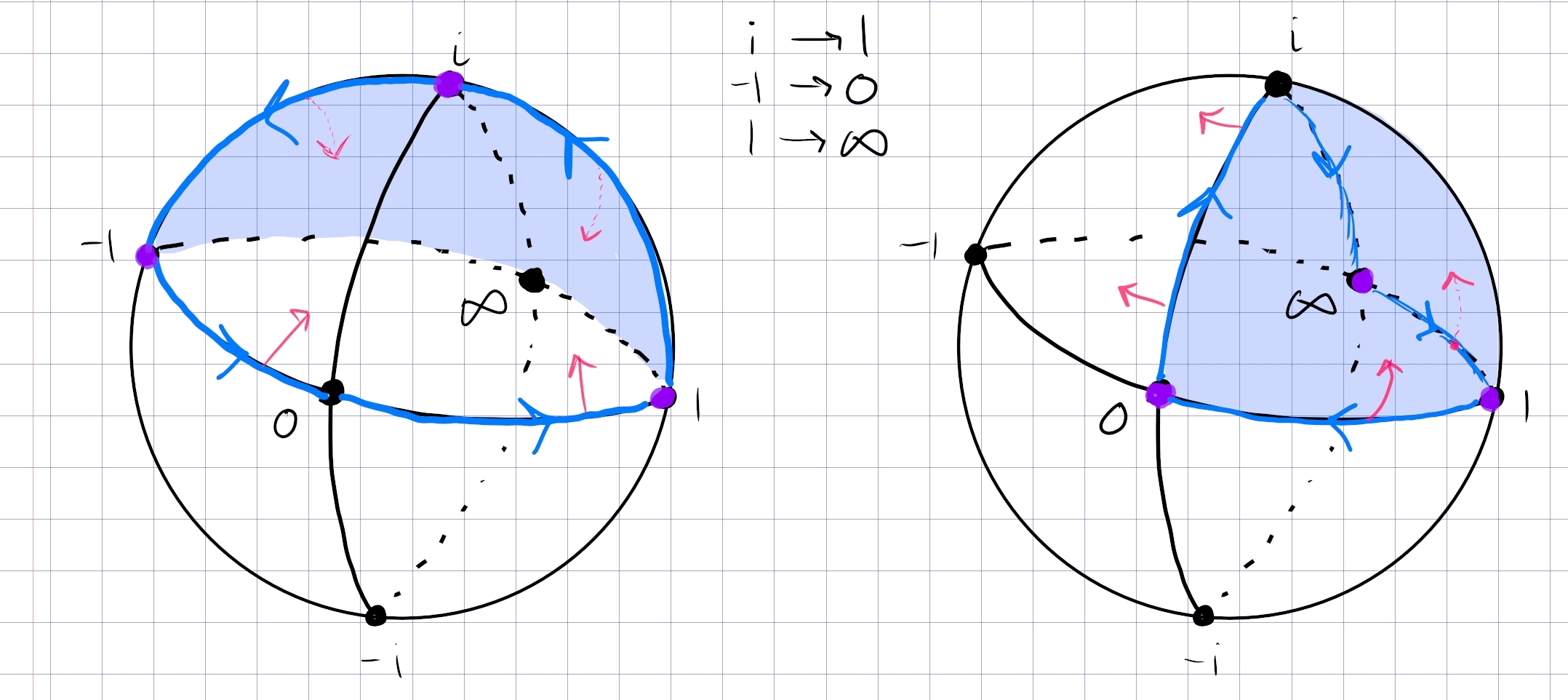
This is the cross-ratio \begin{align*} f(z) = {z+1\over z-1} {i-1\over i+1} .\end{align*}
The image of \({\mathbb{D}}^c \cap{\mathbb{H}}\) is the 1st quadrant \({\mathbb{H}}\cap\Re(z) > 0\). Send this to \({\mathbb{H}}\) with \(z\mapsto z^2\).
Discs and Planes
\({\mathbb{H}}\to{\mathbb{D}}\) #complex/exercise/completed
Find a fractional linear transformation \(T\) which maps \({\mathbb{H}}\) to \({\mathbb{D}}\), and explicitly describe the image of the first quadrant under \(T\).
Unclear to me how to motivate this formula, but choose \(f(z) = {z-i\over z+i}\). Note that
- \(f(-1) = i\)
- \(f(0) = -1\)
- \(f(1) = -i\),
so \({\mathbf{R}}\) oriented from \(-\infty\to\infty\) is sent to \(S^1\) oriented counterclockwise. Since this is conformal, it preserves handedness – noting that \({\mathbb{H}}\) is on the left with respect to \({\mathbf{R}}\), it gets mapped to the left of \(S^1\) with its induced orientation, i.e. the interior of \({\mathbb{D}}\). How to remember: \({\left\lvert {z-i} \right\rvert}<{\left\lvert {z+i} \right\rvert}\) in \({\mathbb{H}}\), since points are closer to \(i\) than \(-i\).
The image of the first quadrant: the claim is that this is \({\mathbb{D}}\cap Q_{34}\). Note that parameterizing seems hard! The naive idea would be to check the image of horizontal lines \(t + ci\) for \(c\) fixed heights and \(t\in (0, \infty)\) the parameterization. Instead consider handedness and where sub-regions go:
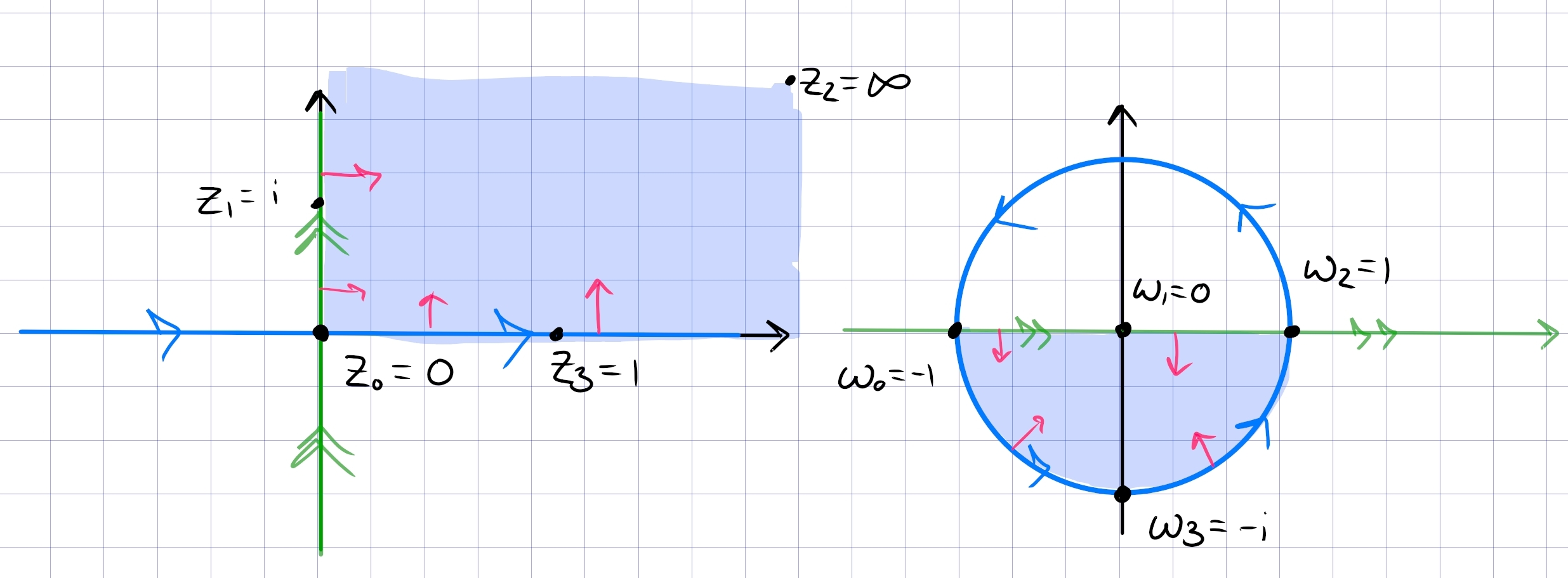
Noting that \(Q_1\) is the bigon enclosed by \(0, \infty\), this maps to a bigon spanned by \(-1, 1\). By handedness, since \(Q_1\) is to the left of \({\mathbf{R}}\), it gets mapped to the left of the image of \({\mathbf{R}}_{>0}\), which is the lower half of the circle.
\({\mathbb{H}}\to{\mathbb{D}}\), cross-ratio #complex/exercise/completed
Find a conformal map \({\mathbb{H}}\to {\mathbb{D}}\) using cross-ratios.
Idea: rotate the upper hemisphere \(({\mathbb{H}})\) of \({\mathbf{CP}}^1\) to make the equator \({{\partial}}{\mathbb{D}}\), “zoom” by placing \(i\) at the center so \(0\to i\mapsto -1\to 0\) and \(i\to \infty\mapsto 0\to 1\). Accomplish this by sending
- \(\infty\to 1\)
- \(i\to 0\)
- \(-i\to \infty\)
Use the cross-ratio \begin{align*} R(z) \coloneqq(z, \infty, i, -i) = {z-i \over z-(-i)} {\infty - (-i) \over \infty - i} = {z-i\over z+i} .\end{align*}
Checking that this works:
- If \(z\in {\mathbf{R}}\) then \({\left\lvert {z-i} \right\rvert} = {\left\lvert {z+i} \right\rvert}\) so \({\left\lvert {F(z)} \right\rvert} = 1\).
- If \(z\in {\mathbb{H}}\) then \({\left\lvert {z-i} \right\rvert}\leq {\left\lvert {z+i} \right\rvert}\) so \({\left\lvert {F(z)} \right\rvert}< 1\).
\({\mathbb{D}}\to{\mathbb{H}}\) #complex/exercise/completed
Find a conformal map from \({\mathbb{D}}\) to \({\mathbb{H}}\).
Note that the standard Cayley map \(f(z)\coloneqq{z-i\over z+i}\) sends \({\mathbb{H}}\to {\mathbb{D}}\). Why this is true: \({\left\lvert {f(z)} \right\rvert} < 1\), since \({\left\lvert {z-i} \right\rvert} < {\left\lvert {z+i} \right\rvert}\) for \(z\in {\mathbb{H}}\). Finding an explicit inverse: \begin{align*} w &= {z-i\over z+i} \\ \implies w(z+i) - (z-i) &= 0 \\ \implies z &= -i {w+1\over w-1} ,\end{align*} which is the desired map. Why the image is in \({\mathbb{H}}\): it suffices to show that \(\Im(f(z)) > 0\) for all \(z\in {\mathbb{D}}\). Write \(z = x+iy\) and note that \(\Im(iz) = \Re(z)\), then \begin{align*} \Im(f(z)) &= \Re\qty{1-z\over 1+z} \\ &= \Re\qty{1-x-iy \over 1+x+iy} \\ &= \Re\qty{1-x^2-y^2 - i2y \over 1+x^2 + y^2} \\ &= {1-(x^2+y^2) \over 1+(x^2+y^2) } \\ &> 0 ,\end{align*} since \(x^2+y^2<1\) for \(x+iy \in {\mathbb{D}}\).
Upper half-disc to \({\mathbb{D}}\) #complex/exercise/completed
Find a conformal map from \(\left\{{z\in {\mathbf{C}}{~\mathrel{\Big\vert}~}{\left\lvert {z} \right\rvert} < 1, \Im(z) > 0}\right\} = {\mathbb{D}}\cap{\mathbb{H}}\) to \({\mathbb{D}}\).
Note that \(z\mapsto z^2\) doesn’t actually work, because the image is \({\mathbb{D}}\setminus{\mathbf{R}}_{\geq 0}\) and has a slit deleted. Instead compose:
- \(z\mapsto i{z-1\over z+1}\), which maps \({\mathbb{D}}\to {\mathbb{H}}\) and restricts to map \({\mathbb{D}}\cap{\mathbb{H}}\to Q_1\).
- \(z\mapsto z^2\), which maps \(Q_1\to {\mathbb{H}}\)
- \(z\mapsto {z-i\over z+i}\) which maps \({\mathbb{H}}\to {\mathbb{D}}\).
In parts:
- Use \(z\mapsto z^{-1}\) to send \({\mathbb{H}}\cap{\mathbb{D}}\) to \(Q_{34} \cap{\mathbb{D}}^c\).
- Use \(z\mapsto -z\) to map this to \({\mathbb{H}}\cap{\mathbb{D}}^c\)
- Use \(z\mapsto {1\over 2}(z+z^{-1})\) to map \({\mathbb{H}}\cap{\mathbb{D}}^c\) to \({\mathbb{H}}\)
- Then use the Cayley map \(z\mapsto {z-i\over z+i}\) to map \({\mathbb{H}}\to {\mathbb{D}}\).
Upper half-disc to \({\mathbb{H}}\) #complex/exercise/completed
Find a conformal map from the upper half-disc to the upper half-plane.
- \(z\mapsto {1+z\over 1-z}\) is a standard map \({\mathbb{D}}\to Q_{14}\) which restricts to \({\mathbb{D}}\cap{\mathbb{H}}\to Q_1\)
- \(z\mapsto z^2\) unwraps \(Q_1\to {\mathbb{H}}\).
\({\mathbb{D}}^c \cap{\mathbb{H}}\to{\mathbb{H}}\) #complex/exercise/completed
Find a conformal map \({\mathbb{D}}^c \cap{\mathbb{H}}\to {\mathbb{H}}\).
Claim: the map \(f(z) \coloneqq z+z^{-1}\) works. Consider the images of circles \(\gamma_r(t) \coloneqq rei^{t}\) where \(t\in [-\pi, \pi]\). For \(r=1\), \begin{align*} f(\gamma_1(t)) = e^{it} + e^{-it} = 2\cos(t) ,\end{align*} which sweeps out \([-2, 2]\) twice. For arbitrary \(r\), \begin{align*} f(\gamma_r(t)) = re^{it} + r^{-1}e^{-it} = (r+r^{-1})\cos(t) +i(r-r^{-1})\sin(t) ,\end{align*} which sweeps out an ellipse with horizontal radius \(r+r^{-1}\) and vertical radius \(r-r^{-1}\). For \(1<r<\infty\), these sweep out all of \({\mathbf{C}}\setminus{\mathbb{D}}\). Restricting \(t\in [0, \pi]\), the \(\gamma_r(t)\) are top halves of circles which cover all of \({\mathbb{H}}\setminus{\mathbb{D}}\), and the images \(f(\gamma_r(t))\) are top halves of ellipses which sweep out all of \({\mathbb{H}}\). This includes points inside of \({\mathbb{D}}\cap{\mathbb{H}}\) – this is because for any \(t\in (0, \infty)\), there is always a solution \(r\) to \(t=r-r^{-1}\): \begin{align*} t = r-r^{-1}\implies r^2-tr-1 \implies r = {t \pm \sqrt{t^2+4}\over 2} .\end{align*} So there is an image ellipse at that vertical height. Since every point \(z_0\in {\mathbb{H}}\) is on an ellipse of some vertical height \(t\), \({\mathbb{H}}\) is in the image.
That this map is conformal: a computation shows \(f'(z) = 1 + {1\over r^2}\), which vanishes only at \(z=\pm 1\). Since these are not in the domain, the derivative is nonvanishing, making \(f\) conformal.
Slits
Find a conformal map \begin{align*} {\mathbb{D}}\setminus\left[ {1\over 2}, 1\right) \to {\mathbb{D}} .\end{align*}
The picture:
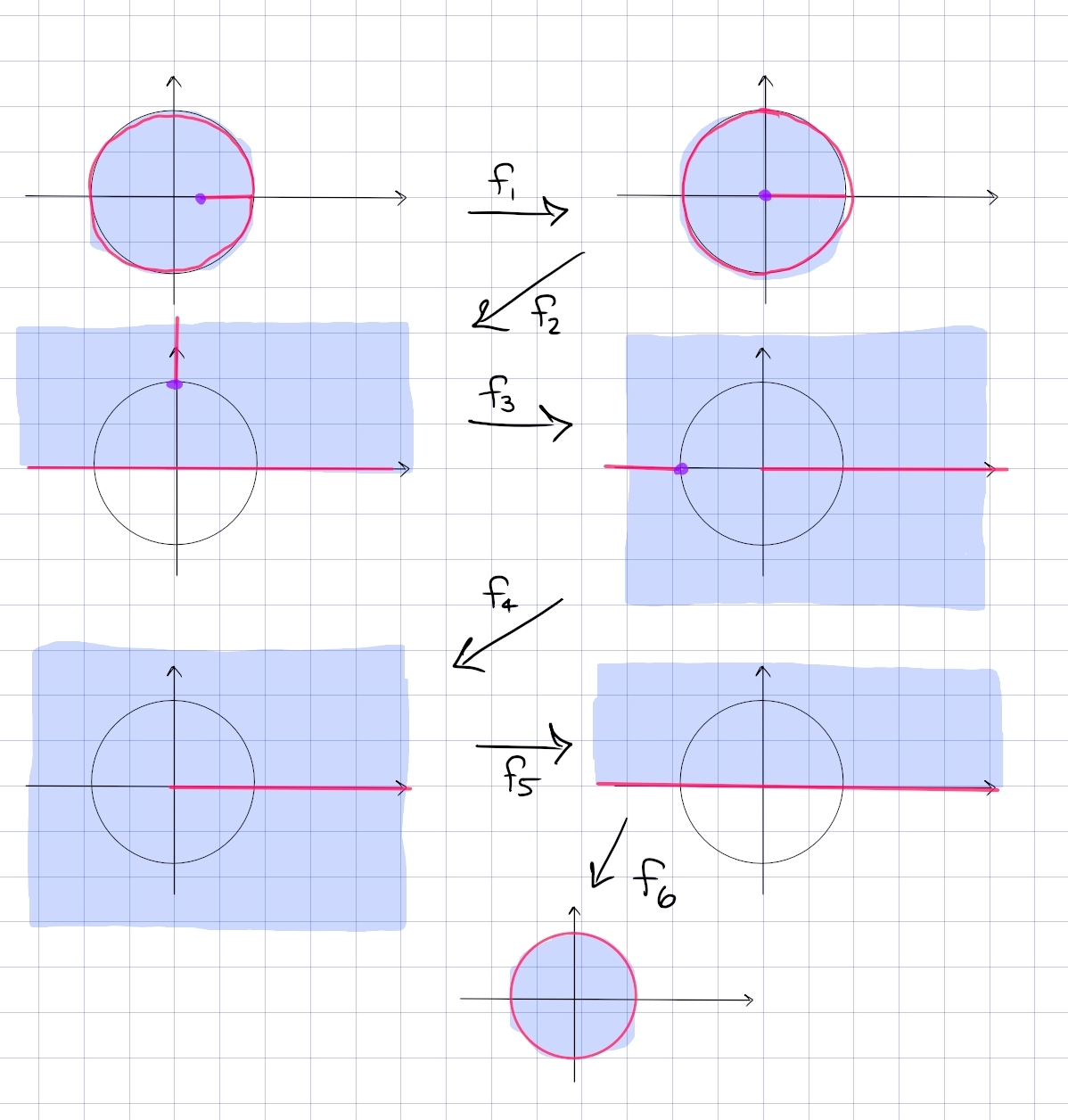
In steps:
-
\(f_1\): send \(1/2\to 0\) and \(1\to 1\) in order to lengthen the slit. Mobius transformations preserve lines, so take \(f_1(z) = {z-1/2 \over 1-1/2}\). New domain: \({\mathbb{D}}\setminus[0, 1)\).
-
\(f_2\): send \({\mathbb{D}}\to {\mathbb{H}}\) and keep track of the slit. Use the standard inverse to the Cayley transform, \(f_2(z) = i{1-z\over 1+z}\). New domain: \({\mathbb{H}}\setminus[i, i\infty)\), noting that \({\mathbb{H}}\) is the open half-plane.
-
\(f_3\): rotate the slit so it becomes a line segment from \(-1\) to \(1\) passing through \(\infty\). Use \(f_3(z) = z^2\). New domain: \({\mathbf{C}}\setminus\qty{(-\infty, 1] \cup[1, \infty) }\)
-
\(f_4\): move the slit off to infinity to be left with a ray, so send \(-1\to \infty\) and \(0\to 0\). Take \(f_4(z) = {z\over z+1}\), the new domain is \({\mathbf{C}}\setminus[0, \infty)\).
-
\(f_5\): fold it back. Branch cut log along \([0, \infty)\) to define \(f_5(z) = z^{1\over 2}\), so the new domain is \({\mathbb{H}}\).
-
\(f_6\): apply the standard Cayley transform \(f_6(z) = {i-z\over i+z}\)
8 #complex/exercise/work
Let \(D\) be the region obtained by deleting the real interval \([0, 1)\) from \({\mathbb{D}}\); find a conformal map from \(D\) to \({\mathbb{D}}\).
9 #complex/exercise/work
Find a conformal map from \({\mathbf{C}}\setminus\left\{{x\in {\mathbf{R}}{~\mathrel{\Big\vert}~}x\leq 0}\right\}\) to \({\mathbb{D}}\).
10 #complex/exercise/work
Find a conformal map from \({\mathbf{C}}\setminus\left\{{x\in {\mathbf{R}}{~\mathrel{\Big\vert}~}x\geq 1}\right\}\) to \({\mathbb{D}}\).
11 #complex/exercise/work
Find a bijective conformal map from \(G\) to \({\mathbb{H}}\), where \begin{align*} G \coloneqq\left\{{z\in {\mathbf{C}}{~\mathrel{\Big\vert}~}{\left\lvert {z-1} \right\rvert} < \sqrt 2,\, {\left\lvert {z+1} \right\rvert} < \sqrt 2}\right\} \setminus [0, i) .\end{align*}
Strips
Horizontal strip to \({\mathbb{H}}\) #complex/exercise/completed
Find a conformal map from the strip \(\left\{{z\in {\mathbf{C}}{~\mathrel{\Big\vert}~}0 < \Im(z) < 1}\right\}\) to \({\mathbb{H}}\).
In steps:
- Dilate by \(z\mapsto \pi z\) to get \(0<\Im(z) < \pi\).
- Exponentiate by \(z\mapsto e^z\) to get \({\mathbb{H}}\).
Why \(e^z\) works: apply \(\operatorname{Log}\) to \({\mathbb{H}}\), use polar coordinates to write \(w=re^{i\theta}\) with \(0<\theta<\pi\) and note \begin{align*} \operatorname{Log}(w) = \ln{\left\lvert {w} \right\rvert} +i\operatorname{Arg}(w) = \ln(r) + i\theta ,\end{align*} and noting that the image of \(\ln({-})\) is all of \({\mathbf{R}}\).
Lunes
Intersection of circles
Find a conformal map \(L\to {\mathbb{D}}\) where \begin{align*} L\coloneqq\left\{{{\left\lvert {z - i } \right\rvert} < \sqrt 2}\right\} \cap\left\{{{\left\lvert {z+i} \right\rvert} < \sqrt 2}\right\} ,\end{align*} i.e. a lune with vertices \(-1\) and \(1\).
The key insight: for lunes, map the corners to \(0\) and \(\infty\); this yields a sector. Here we want \(-1\mapsto 0\) and \(1\mapsto \infty\), so \(f(z) = {z+1\over z-1}\) gets things started.
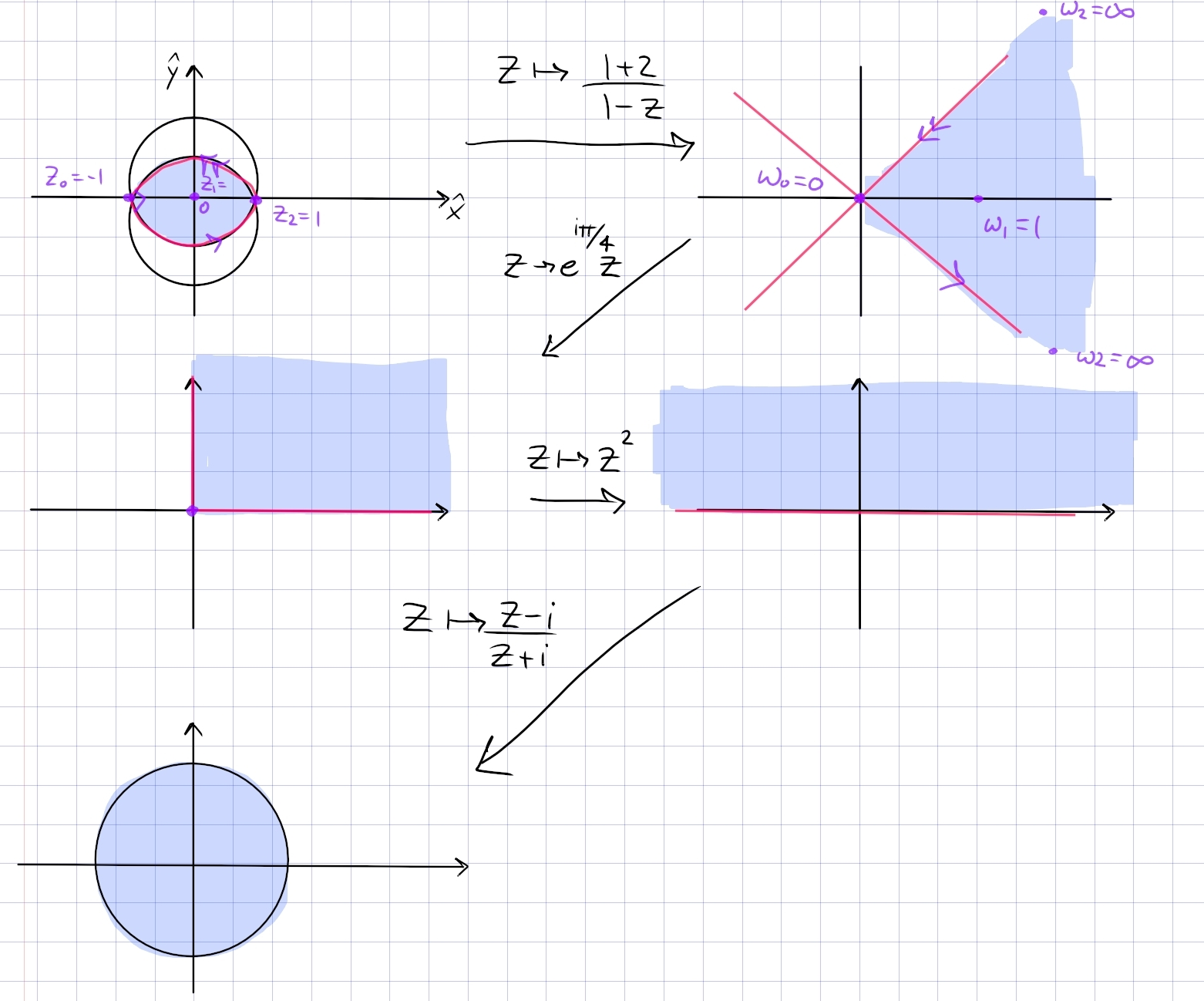
In steps:
- \(z\mapsto {1+z\over 1-z}\) sends the lune to the sector \(\operatorname{Arg}(z) \in (-\pi/4, \pi/4)\), since it fixes and must be symmetric about the real axis, and preserves the right angle between the circles at \(z=-1\).
- \(z\mapsto e^{i\pi/4}z\) to rotate this into \(Q_1\).
- \(z\mapsto z^2\) to dilate into \({\mathbb{H}}\).
- \(z\mapsto {z-i\over z+i}\) the standard Cayley map \({\mathbb{H}}\to{\mathbb{D}}\).
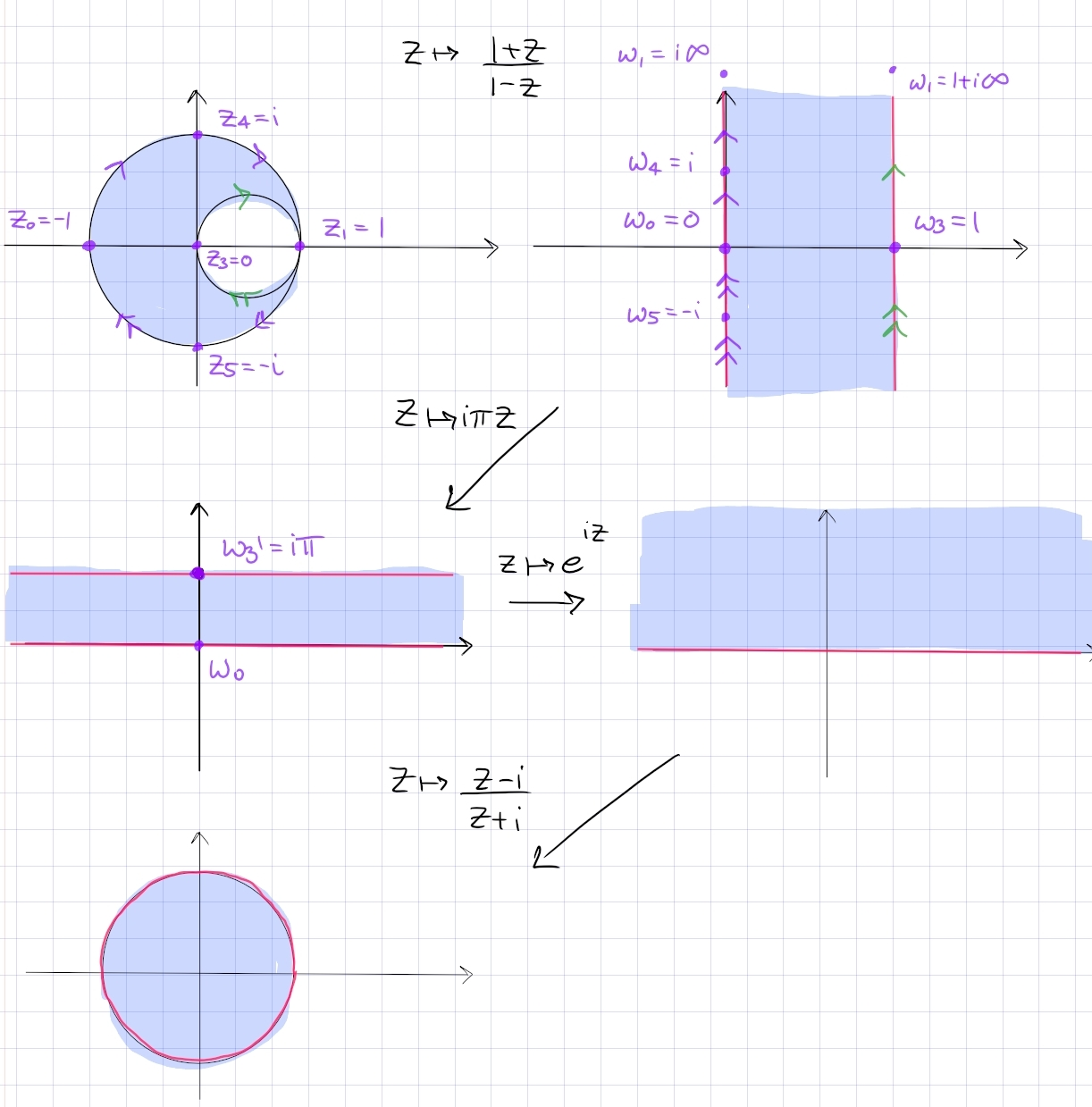
Lune with one intersection point
Find a conformal map: \begin{align*} {\mathbb{D}}\setminus\left\{{{\left\lvert {z - {1\over 2}} \right\rvert} = {1\over 2} }\right\} \to {\mathbb{D}} .\end{align*}
The picture:
-
Key insight: send the point of tangency to \(\infty\) to get parallel lines. Send \(z\mapsto {1+z \over 1-z}\) to send \(-1\to 0, 0\to 1, 1\to \infty\) to get a vertical strip.
-
Rotate and dilate: \(z\mapsto i\pi z\) to get a strip \({\mathbf{R}}\times i(0, \pi)\).
-
Standard exponential \(z\mapsto e^{iz}\) sends this to \({\mathbb{H}}\).
-
Standard Cayley \(z\mapsto {z-i \over z+i}\) sends this to \({\mathbb{D}}\).
4 #complex/exercise/work
Find a conformal map from \(\left\{{z\in {\mathbf{C}}{~\mathrel{\Big\vert}~}{\left\lvert {z-i} \right\rvert} > 1,\, \Re(z) > 0}\right\}\) to \({\mathbb{H}}\).
5 #complex/exercise/work
Find a conformal map from \(\left\{{z\in {\mathbf{C}}{~\mathrel{\Big\vert}~}{\left\lvert {z} \right\rvert} < 1,\, {\left\lvert {z - {1\over 2}} \right\rvert} > {1\over 2} }\right\}\) to \({\mathbb{D}}\).
6 #complex/exercise/work
Find a conformal map from \(\left\{{{\left\lvert {z-1} \right\rvert} < 2}\right\} \cap\left\{{{\left\lvert {z+1} \right\rvert} < 2}\right\}\) to \({\mathbb{H}}\).
13 #complex/exercise/work
Find a conformal map from \(D = \{z :\ |z| < 1,\ |z - 1/2| > 1/2\}\) to the unit disk \(\Delta=\{z: \ |z|<1\}\).
Sectors
Find a conformal map from the sector \(\left\{{\operatorname{Arg}(z) \in (0, \alpha)}\right\} \to {\mathbb{D}}\).
The picture:
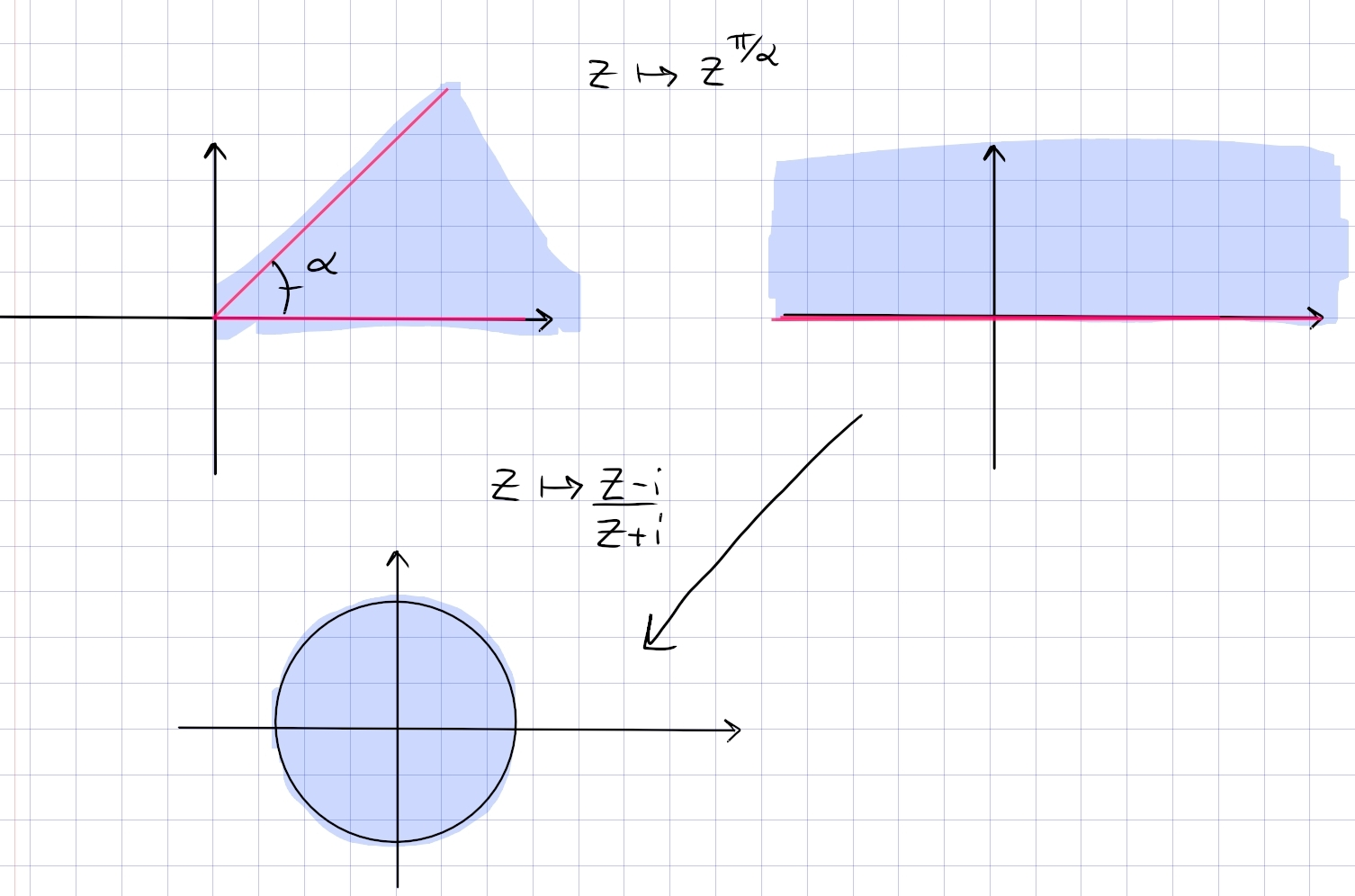
In steps:
- Map the sector to \({\mathbb{H}}\) using \(z\mapsto z^{\pi/\alpha}\), choosing a branch cut for \(\operatorname{Log}\) along \({\mathbf{R}}_{\leq 0}\).
- Map \({\mathbb{H}}\to {\mathbb{D}}\) using the standard \(z\mapsto {z-i\over z+i}\).
Joukowski-Type Regions
Map \({\mathbf{C}}\setminus[-1, 1]\) to \({\mathbb{D}}\).
In steps:
-
Send \(-1\to 0\) and \(1\to \infty\) with \(z\mapsto {z+1\over z-1}\). Checking that \(f(0) = -1\), this yields \({\mathbf{C}}\setminus{\mathbf{R}}_{\leq 0}\).
-
Unwrap with \(z\mapsto \sqrt{z}\) to obtain the right half-plane \(-\pi/2<\operatorname{Arg}(z) < \pi/2\).
-
Apply the rotated Cayley map \(z\mapsto {z-1\over z+1}\) to map this to \({\mathbb{D}}\).
Note that the composition is \begin{align*} {\sqrt{z+1\over z-1} -1 \over \sqrt{z+1\over z-1} +1} &= { \qty{ \sqrt{z+1} - \sqrt{z-1}}^2 \over (z+1)-(z-1) } \\ &= z - \sqrt{z^2-1} ,\end{align*} which has inverse \(z\mapsto {1\over 2}\qty{z+{1\over z}}\).
Misc
Find a conformal map that sends \(i{\mathbf{R}}\) to \({\left\lvert {z-{1\over 2}} \right\rvert} = {1\over 2}\).
-
The double angle formulas: \begin{align*} \sin(2t) = {2\tan(t) \over 1+\tan^2(t)} && \cos(2t) = {1-\tan^2(2t) \over 1+\tan^2(t)} .\end{align*}
-
Parameterize a line by \(x=\tan(t)\) for \(t\in (-\pi/2, \pi/2)\)
-
The methods in SS Theorem 1.2: particularly the boundary behavior of \(F(z) \coloneqq{i-z\over i+z}\), where \(F({\mathbf{R}}) = \left\{{\cos(2t)+i\sin(2t) = e^{2it} {~\mathrel{\Big\vert}~}t\in (-\pi/2, \pi/2)}\right\}\).
-
Nyquist plots: a common applied problem, essentially computing the image \(F(i{\mathbf{R}})\).
Idea: need the line \(-i\infty\to 0 \to i\infty\) to get mapped to a circle \(0\to 1\to 0\):
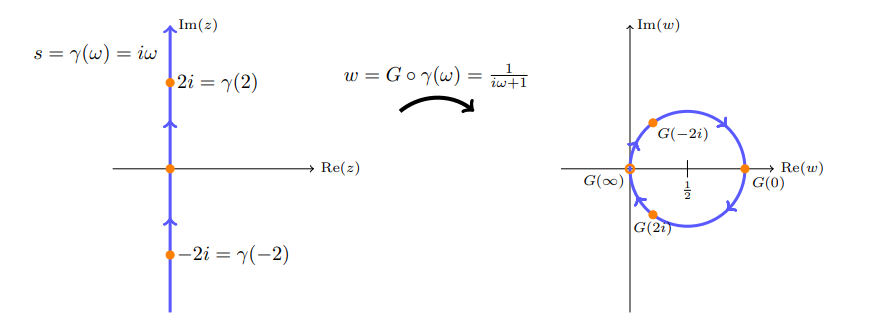
Take the cross ratio \(R(z) = (z, 0, \infty, -1)\) to send
- \(0\to 1\)
- \(\infty\to 0\)
- \(-1\to \infty\)
This yields \begin{align*} R(z) = {z-\infty \over z+1}{0+1\over 0-\infty} = {1\over z+1} .\end{align*} Some deductions:
-
\(R\) preserves circles, so \({\mathbf{R}}\mapsto {\mathbf{R}}\).
- The segment \(0\to\infty\mapsto 1\to 0\)
- The ray \(-1\to 0 \to \infty \mapsto \infty\to 1\to 0\)
- The ray \(-\infty \to -1 \mapsto 0\to -\infty\)
- \(R\) preserves angles, to at \(w=0\), the image of \(i{\mathbf{R}}\) must be orthogonal to \({\mathbf{R}}\), so it’s either a circle or \(i{\mathbf{R}}\) itself.
- Check \(-i\infty \to 0 \to -\infty\mapsto 0\to 1\to 0\), so the image is a circle.
- Parameterize \(i{\mathbf{R}}= \left\{{it{~\mathrel{\Big\vert}~}t\in {\mathbf{R}}}\right\}\), then compute the image \begin{align*} f(i{\mathbf{R}}) &= \left\{{{1\over 1+it}}\right\} \\ &= \left\{{1+t\over 1+t^2}\right\} \\ &= \left\{{{1\over 1+t^2} + i {t\over 1+t^2}}\right\} \\ &= \left\{{{1\over 2} \qty{ 1 + {1-t^2\over 1+t^2} } + i{1\over 2}\qty{2t\over 1+t^2}}\right\} \\ &= \left\{{{1\over 2}\qty{1 + \cos(2t) + i\sin(2t)}}\right\} \\ &= \left\{{{1\over 2} + {1\over 2}e^{2it} }\right\} ,\end{align*} which is a circle of radius \(1/2\) about \(1/2\).
Conclusion:
- \(i{\mathbf{R}}\to \left\{{{\left\lvert {z-{1\over 2}} \right\rvert} = {1\over 2} }\right\}\) by \(z\to {1\over 1+z}\).
- The reverse map: \(w\mapsto {1-w\over w}\).
Map \({\mathbb{D}}^c \cap{\mathbb{H}}\) to \({\mathbb{H}}\), sending
- \(-1\to -1\)
- \(i\to 0\)
- \(1\to 1\)
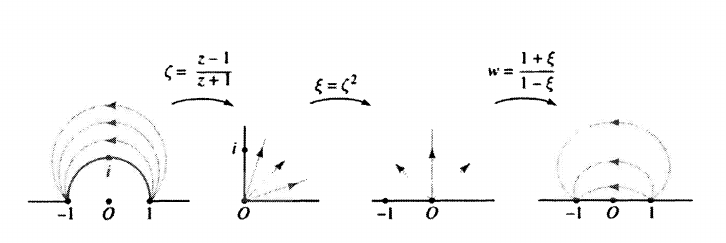
Compose to get: \begin{align*} {1\over z}{z + z^{-1}} .\end{align*}
7 #complex/exercise/work
Let \(\Omega\) be the region inside the unit circle \({\left\lvert {z} \right\rvert} = 1\) and outside the circle \({\left\lvert {z-{1\over 4}} \right\rvert} = {1\over 4}\).
Find an injective conformal map from \(\Omega\) onto some annulus \(\left\{{r < {\left\lvert {z} \right\rvert} < 1}\right\}\) for constant \(r\).
12 #complex/exercise/work
Prove that TFAE for a Möbius transformation \(T\) given by \(T(z) = {az + b \over cz + d}\):
- \(T\) maps \({\mathbf{R}}\cup\left\{{\infty}\right\}\) to itself.
- It is possible to choose \(a,b,c,d\) to be real numbers.
- \(\overline{T(z)} = T(\overline{z})\) for every \(z\in {\mathbf{CP}}^1\).
- There exist \(\alpha\in {\mathbf{R}}, \beta \in {\mathbf{C}}\setminus {\mathbf{R}}\) such that \(T(\alpha) = \alpha\) and \(T(\overline{\beta}) = \overline{T(\beta)}\).