If \(f\) is holomorphic on \(\Omega\setminus\left\{{z_0}\right\}\) where \(z_0\) is an essential singularity, then for every \(V\subset \Omega\setminus\left\{{z_0}\right\}\), \(f(V)\) is dense in \({\mathbf{C}}\).
Equivalently, suppose \(z_{0}\) is an essential isolated singularity of \(f(z)\). Then for every complex number \(w_{0}\), there is a sequence \(z_{n} \rightarrow z_{0}\) such that \(f\left(z_{n}\right) \rightarrow w_{0}\).
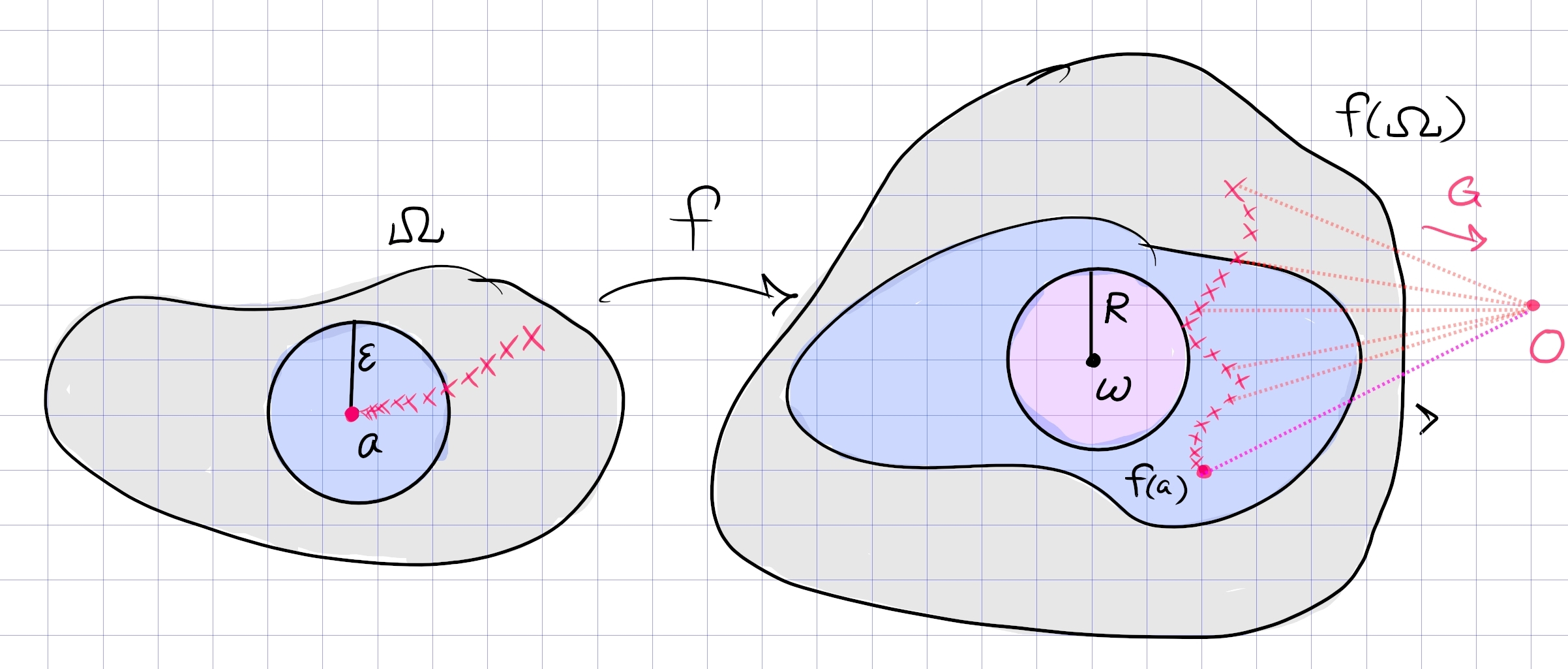
The image of a punctured disc at an essential singularity is dense in \({\mathbf{C}}\).
Let \(f\) have an essential singularity. Suppose toward a contradiction that there exists a \(z_0\in {\mathbf{C}}\), a punctured neighborhood \(\Omega\) of \(z_0\), and \({\varepsilon}> 0\) with \(f(\Omega) \cap{\mathbb{D}}_{\varepsilon}(z_0)\) empty. So \({\left\lvert {f(z) - z_0} \right\rvert}>{\varepsilon}\) for every \(z\in \Omega\). Write \(\tilde \Omega \coloneqq\Omega\cup\left\{{z_0}\right\}\).
Define \(g(z) \coloneqq{1\over f(z) - z_0}\), noting that \(z_0\) is the only singularity of \(g\) in \(\tilde\Omega\), making \(g\) holomorphic on \(\Omega\). We have \({\left\lvert {g(z)} \right\rvert} < {\varepsilon}^{-1}< \infty\) for all \(z\in \Omega\), so \(g\) is bounded in \(\Omega\) and \(z_0\) must be a removable singularity. By Riemann’s removable singularity theorem, \(g\) extends to a holomorphic function on all of \(\tilde\Omega\).
We can now write \(f(z) = {1\over g(z)} + z_0\). If \(g(z_0) = 0\), then it is a zero of some finite order for \(g\), and thus a pole of finite order for \(f\), contradicting that \(z_0\) is essential for \(f\). Otherwise, if \(g(z_0) = w_0\neq 0\), then \begin{align*} {\left\lvert { f(z_0)} \right\rvert} = {\left\lvert { {1\over w_0} + z_0} \right\rvert} \leq {\varepsilon}+ {\left\lvert {z_0} \right\rvert} < \infty ,\end{align*} making \(z_0\) removable and again yielding a contradiction.
Pick \(w\in {\mathbf{C}}\) and suppose toward a contradiction that \(D_R(w) \cap f(V)\) is empty. Consider \begin{align*} g(z) \coloneqq{1\over f(z) - w} ,\end{align*} and use that it’s bounded to conclude that \(z_0\) is either removable or a pole for \(f\).
In detail, from Gamelin:


Exercises
Show that if \(f\) is entire and there exists a disc \({\mathbb{D}}_r(a)\) not intersecting \(f({\mathbf{C}})\), then \(f\) must be constant.
Write \(a\not\in f({\mathbf{C}})\), and replace \(f\) with \(f(z) - a\) so that \(f(a) = 0\) and there is some \({\mathbb{D}}_R(0)\) not intersecting \(f({\mathbf{C}})\). Then \(f(z) \in {\mathbb{D}}_R^c\) for all \(z\in {\mathbf{C}}\), so \({\left\lvert {f(z)} \right\rvert} > R\) for all \(z\). Defining \(G(z) \coloneqq{1\over f(z)}\) yields \({\left\lvert {G(z)} \right\rvert} < R^{-1}\) for all \(z\), making \(G\) bounded. The singularity of \(G\) at \(z=0\) is thus removable, so \(G\) extends to an entire function by Riemann’s removable singularity theorem. By Liouville, \(G\) is constant, so \(f\) is constant.
Find all entire functions \(f\) that satisfy \begin{align*} {\left\lvert {f(z)} \right\rvert} \geq e^{{\left\lvert {z} \right\rvert}} && \forall z\in {\mathbf{C}} .\end{align*}
Claim: there are no such functions. Consider \(g(z) \coloneqq f(z)/e^z\), which is entire since \(e^z\) is nonvanishing. Now \(g\) is entire and \({\left\lvert {g} \right\rvert} \geq 1\) everywhere, so \(\operatorname{im}(g) \cap{\mathbb{D}}\) is empty. This contradicts Casorati-Weierstrass, which requires that \(\operatorname{im}g\) be dense in \({\mathbf{C}}\).
Alternatively, note \(f\neq 0\) by the inequality, so \(1/f\) is bounded and entire and thus constant. However, \(f(z) = c\) contradicts the inequality, since \(e^{{\left\lvert {z} \right\rvert}}\to \infty\) as \({\left\lvert {z} \right\rvert}\to \infty\).
Alternatively, note that \(e^{{\left\lvert {z} \right\rvert}} \geq 1\) for all \(z\), so \(\operatorname{im}(f) \cap{\mathbb{D}}\) is empty, again contradicting Casorati-Weierstrass.
Let \(f\) be entire and define a function \begin{align*} m: [0, \infty) &\to {\mathbf{R}}\\ r &\mapsto \min_{{\left\lvert {z} \right\rvert} = r} {\left\lvert {f(z)} \right\rvert} .\end{align*} Suppose \(\tilde m \coloneqq\lim_{r\to \infty}m(r)\) exists and is a finite positive real number, and show that \(f\) is constant.
Hint: consider \(g(z) \coloneqq f(1/z)\).