Tie’s Extra Questions: Fall 2015 (Computing area) #complex/exercise/completed
Let \(f(z) = \sum_{n=0}^\infty c_n z^n\) be analytic and one-to-one in \(|z| < 1\). For \(0<r<1\), let \(D_r\) be the disk \(|z|<r\). Show that the area of \(f(D_r)\) is finite and is given by \begin{align*} S = \pi \sum_{n=1}^\infty n |c_n|^2 r^{2n} .\end{align*}
Note that in general the area of \(f(D_1)\) is infinite.
Since \(f\) is injective, \(f'\) is nonvanishing in \(\Omega \coloneqq{\left\lvert {z} \right\rvert} \leq r\). A computation: \begin{align*} \mu(f({\mathbb{D}}_r)) &= \int_{{\mathbb{D}}_r} {\left\lvert {f'(z)} \right\rvert}\,dz\\ &= \int_{{\mathbb{D}}_r} f'(z) \overline{f'(z)} \,dz\\ &= \int_{{\mathbb{D}}_r} \qty{\sum_{j\geq 1} jc_j z^{j-1} } \overline{ \qty{\sum_{k\geq 1} kc_k z^{k-1}}} \,dz\\ &= \int_{{\mathbb{D}}_r} \qty{\sum_{j\geq 1} j c_j z^{j-1} } { \qty{\sum_{k\geq 1} k \overline{c_k} \overline{z}^{k-1} }} \,dz\\ &= \int_{{\mathbb{D}}_r} \sum_{j, k\geq 1} jk c_j \overline{c_k} z^{j-1}\overline{z}^{k-1}\,dz\\ &= \int_0^R\int_0^{2\pi} \sum_{j, k\geq 1} jk c_j \overline{c_k} (re^{it})^{j-1} (re^{-it})^{k-1} r\,dr\,dt\\ &= \int_0^R\int_0^{2\pi} \sum_{j, k\geq 1} jk c_j \overline{c_k} r^{j+k-1} e^{i(j-k)t} \,dr\,dt\\ &= \int_0^R \sum_{k\geq 1} k^2 {\left\lvert {c_k} \right\rvert}^2 r^{2k-1} \cdot 2\pi \,dt\\ &= \sum_{k\geq 1} k^2 {\left\lvert {c_k} \right\rvert}^2 {r^{2k} \over 2k}\Big|_{r=0}^R \\ &= \pi \sum_{k\geq 1} k {\left\lvert {c_k} \right\rvert}^2 R^{2k} .\end{align*}
Tie’s Extra Questions: Fall 2015 (Variant) #complex/exercise/completed
Let \(f(z) = \sum_{n= -\infty}^\infty c_n z^n\) be analytic and one-to-one in \(r_0< |z| < R_0\). For \(r_0<r<R<R_0\), let \(D(r,R)\) be the annulus \(r<|z|<R\). Show that the area of \(f(D(r,R))\) is finite and is given by \begin{align*}S = \pi \sum_{n=- \infty}^\infty n |c_n|^2 (R^{2n} - r^{2n}).\end{align*}
See above solution: all goes identically up until the integral over \(r\) values, just replace \(\int_0^R\) with \(\int_r^R\).
Spring 2019.1 #complex/qual/work
Define
\begin{align*} E(z)=e^{x}(\cos y+i \sin y) . \end{align*}
- Show that \(E(z)\) is the unique function analytic on \(\mathbb{C}\) that satisfies
\begin{align*} E^{\prime}(z)=E(z), \quad E(0)=1 . \end{align*}
- Conclude from the first part that \begin{align*} E(z)=\sum_{n=0}^{\infty} \frac{z^{n}}{n !} .\end{align*}
Recurrences #complex/qual/work
Let \(x_0 = a, x_1 = b\), and set \begin{align*} x_n \coloneqq{x_{n-1} + x_{n-2} \over 2} \quad n\geq 2 .\end{align*}
Show that \(\left\{{x_n}\right\}\) is a Cauchy sequence and find its limit in terms of \(a\) and \(b\).
With some substitution, one can compute \begin{align*} {\left\lvert {x_n - x_{n-1}} \right\rvert} = {\left\lvert {{1\over 2} x_{n-1} + {1\over 2} x_{n-2} - x_{n-1}} \right\rvert} = {1\over 2} {\left\lvert {x_{n-1} - x_{n-2}} \right\rvert} ,\end{align*} which holds for all \(n\). This is enough to show that the sequence is contractive, i.e. \begin{align*} {\left\lvert {x_n - x_{n-1}} \right\rvert} = c {\left\lvert {x_{n-1} - x_{n-2}} \right\rvert} && c\in (0, 1) .\end{align*}
Apply this recursively yields \begin{align*} {\left\lvert {x_n - x_{n-1}} \right\rvert} = \qty{1\over 2}^{n-1} {\left\lvert {b-a} \right\rvert} \overset{n\to\infty}\longrightarrow 0 ,\end{align*} since \({\left\lvert {b-a} \right\rvert}\) is a constant. So in fact \(x_n\) is convergent and thus Cauchy convergent.
Note: to compare \({\left\lvert {x_i - x_j} \right\rvert}\) directly, assume \(i>j\) and apply the above estimate \(i-j+1\) on \({\left\lvert {x_i - x_{i-1}} \right\rvert}, {\left\lvert {x_{i-1} - x_{i-2}} \right\rvert}, \cdots\) to reduce to this case. This yields something like \begin{align*} {\left\lvert {x_i - x_j} \right\rvert} = \qty{1\over 2}^{i-j+1}{\left\lvert {x_{j} - x_{j-1}} \right\rvert} = \qty{1\over 2}^{i-j+1} \qty{1\over 2}^{j-1} {\left\lvert {b-a} \right\rvert}\to 0 .\end{align*} One could equivalently use the triangle inequality and a partial geometric sum to write \begin{align*} {\left\lvert {x_i - x_j} \right\rvert} \leq \sum_{j\leq k \leq i-1} {\left\lvert {x_{k+1} - x_{k}} \right\rvert} \implies {\left\lvert {x_i - x_j} \right\rvert} \leq c^j\qty{1\over 1-c}{\left\lvert {b-a} \right\rvert} .\end{align*}
Computing its limit: the usual trick of setting \(L \coloneqq\lim x_n = \lim x_{n-1} = \lim x_{n-2}\) only yields \(L = {L + L \over 2}\) here, and thus no information. Instead assume \(x_n = r^n\) is geometric, then \begin{align*} 2x_n - x_{n-1} - x_{n-2} = 0 \implies 2r^n - r^{n-1} - r^{n-2} = 0 \implies 2r^2 - r - 1 = 0 \iff (2r+1)(r-1) = 0 \implies r = -1/2, 1 .\end{align*} Write a general solution as \begin{align*} x_n = c_1 (-1/2)^n + c_2 (1)^n = c_1 (-1/2)^n + c_2 ,\end{align*} and solve for initial conditions: \begin{align*} x_0: \quad a &= c_1 + c_2 \\ x_1: \quad b &= (-1/2)c_1 + c_2 \\ \\ \implies { \begin{bmatrix} {1} & {1} \\ {-1/2} & {1} \end{bmatrix} } \begin{bmatrix} c_1 \\ c_2 \end{bmatrix} &= \begin{bmatrix} a \\ b \end{bmatrix} \\ \implies \begin{bmatrix} c_1 \\ c_2 \end{bmatrix} &= {1\over 1 + (1/2)} { \begin{bmatrix} {1} & {-1} \\ {1/2} & {1} \end{bmatrix} } \begin{bmatrix} a \\ b \end{bmatrix} \\ &= \qty{1\over 3} { \begin{bmatrix} {2} & {-2} \\ {1} & {2} \end{bmatrix} } \begin{bmatrix} a \\ b \end{bmatrix} \\ &= \qty{1\over 3} \begin{bmatrix} 2a-2b \\ a+b \end{bmatrix} .\end{align*}
So the general solution is \begin{align*} x_n = {2\over 3}(a-b) \qty{-1\over 2}^n + {1\over 3}(a+b)\overset{n\to \infty}\longrightarrow \qty{1\over 3}(a+b) .\end{align*}
Uniform continuity #complex/qual/work
Suppose \(f:{\mathbf{R}}\to{\mathbf{R}}\) is continuous and \(\lim_{x\to \pm \infty} f(x) = 0\). Prove that \(f\) is uniformly continuous.
Fix \({\varepsilon}>0\), we need to find a \(\delta = \delta({\varepsilon})\) such that \begin{align*} {\left\lvert {x-y} \right\rvert}<\delta \implies {\left\lvert {f(x) - f(y)} \right\rvert} < {\varepsilon}&& \forall x, y\in {\mathbf{R}} .\end{align*} Use that \(\lim_x\to \pm \infty f(x) = 0\) to choose \(M\gg 0\) such that \begin{align*} {\left\lvert {x} \right\rvert} \geq M \implies {\left\lvert {f(x)} \right\rvert} \leq {\varepsilon}/2 ,\end{align*} then \begin{align*} {\left\lvert {x} \right\rvert}, {\left\lvert {y} \right\rvert} \geq M \implies {\left\lvert {f(x) - f(y)} \right\rvert} \leq {\left\lvert {f(x)} \right\rvert} + {\left\lvert {f(y)} \right\rvert} \leq {\varepsilon} .\end{align*} So in this region choose (say) \(\delta_1 < {\varepsilon}\) to ensure that \(B_\delta(x), B_\delta(y) \subseteq [-M, M]^c\). On \([-M, M]\), note that this region is compact and \(f\) continuous on a compact set implies uniformly continuous. So use this to choose \(\delta_2 = \delta_2({\varepsilon})\) in this region to ensure \({\left\lvert {f(x) - f(y)} \right\rvert} < {\varepsilon}\).
This handles the cases \(x, y \in (M, M)^c\), or \(x,y\in [M, M]\), so it only remains to handle \(x\in [M, M]\) and \(y\in (M, M)^c\) (wlog, relabeling \(x,y\) if necessary). In this case, use the triangle inequality: \begin{align*} {\left\lvert {f(x) - f(y)} \right\rvert} &= {\left\lvert {f(x) - f(M) + f(M) -f(y)} \right\rvert} \\ &\leq {\left\lvert {f(x) - f(M)} \right\rvert} + {\left\lvert {f(M) -f(y)} \right\rvert} \\ &\leq {\varepsilon}+ {\left\lvert {f(M)} \right\rvert} + {\left\lvert {f(y)} \right\rvert} \\ &\leq {\varepsilon}+ {\varepsilon}+ {\varepsilon} ,\end{align*} where we’ve used that \(M, y\in (M, M)^c\) to apply the first bound and \(M, x\in [M, M]\) to apply the second.
Negating uniform continuity #complex/qual/completed
Tie, Fall 2009
Show that \(f(z) = z^2\) is uniformly continuous in any open disk \(|z| < R\), where \(R>0\) is fixed, but it is not uniformly continuous on \(\mathbb C\).
A direct computation: fix \({\varepsilon}>0\) and suppose \({\left\lvert {z-w} \right\rvert} < R\). Then \begin{align*} {\left\lvert {z^2-w^2} \right\rvert} &= {\left\lvert {z-w} \right\rvert}{\left\lvert {z+w} \right\rvert} \\ &\leq \delta \qty{{\left\lvert {z} \right\rvert} + {\left\lvert {w} \right\rvert}} \\ &\leq \delta \cdot 2R ,\end{align*} so choose \(\delta < { {\varepsilon}\over 2R}\) to get uniform continuity on \({\mathbb{D}}_{R/2}(0)\).
To see \(f\) can’t be uniformly continuous on \({\mathbf{C}}\), take \({\varepsilon}\coloneqq c\) any constant and suppose the appropriate \(\delta\) exists. We’ll look for a bad pair of \(z, w\), so take \(w = z + {1\over 2}\delta\). This would imply \begin{align*} {\left\lvert {z^2 - w^2} \right\rvert} &= {\left\lvert {z^2 - (z+\delta)^2} \right\rvert} \\ &= {\left\lvert {-2z\delta - \delta^2} \right\rvert} \\ &= {\left\lvert {2z\delta + \delta^2} \right\rvert} \\ &= \delta {\left\lvert {2z + \delta} \right\rvert} \\ &\overset{{\left\lvert {z} \right\rvert}\to\infty}\longrightarrow\infty ,\end{align*} using the \(\delta = \delta({\varepsilon})\) can’t depend on \(z\) or \(w\), and is thus constant in this expression. This contradicts that \({\left\lvert {z^2-w^2} \right\rvert} < {\varepsilon}= c < \infty\).
Non-continuously differentiable #complex/qual/completed
Give an example of a function \(f:{\mathbf{R}}\to {\mathbf{R}}\) that is everywhere differentiable but \(f'\) is not continuous at 0.
The standard example: \begin{align*} f(x) \coloneqq \begin{cases} x^2\sin\qty{1\over x} & x\neq 0 \\ 0 & x=0. \end{cases} .\end{align*}
Away from zero, this is clearly differentiable since we can just compute the derivative by the chain rule. It turns out that \begin{align*} f'(x) = \begin{cases} 2x\sin\qty{1\over x} + x^2 \cos\qty{1\over x}\qty{-1\over x^2} = 2x\sin\qty{1\over x} - \cos\qty{1\over x} & x\neq 0 \\ 0 & x=0. \end{cases} .\end{align*} Here we check differentiability and compute the derivative at \(x=0\) directly: \begin{align*} {f(x) - f(0) \over x-0} = {x^2\sin\qty{1\over x} - 0 \over x-0} = x\sin\qty{1\over x} \overset{x\to 0}\longrightarrow 0 ,\end{align*} using that \(-x \leq {\left\lvert {x\sin \qty{1\over x}} \right\rvert}\leq x\).
But now notice that the \(\cos\qty{1\over x}\) term in \(f'\) isn’t enveloped by an \(x^c\) term, so \(\lim_{x\to 0} f'(x)\) does not exist for oscillatory reasons:
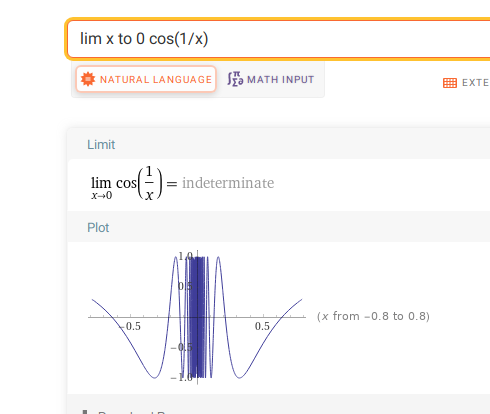
In particular, \(\lim_{x\to 0}f'(x) \neq f'(0) = 0\).
Uniformly convergent + uniformly continuous #complex/qual/completed
Suppose \(\left\{{g_n}\right\}\) is a uniformly convergent sequence of functions from \({\mathbf{R}}\) to \({\mathbf{R}}\) and \(f:{\mathbf{R}}\to {\mathbf{R}}\) is uniformly continuous. Prove that the sequence \(\left\{{f\circ g_n}\right\}\) is uniformly convergent.
Uniformly convergent means that \({\left\lVert {g_i - g_j} \right\rVert}_{\infty} \to 0\), so \(\sup_{x\in X}{\left\lvert {g_i(x)-g_j(x)} \right\rvert} \overset{i, j\to\infty}\longrightarrow 0\). We want to show that given \({\varepsilon}\) we can find \(N_0\) such that \(i, j > N_0\) yields \begin{align*} \sup_{x\in X}{\left\lvert { f\circ g_i(x) - f\circ g_j(x) } \right\rvert} < {\varepsilon} .\end{align*}
Fix \({\varepsilon}> 0\), then choose \(\delta_1 = \delta_1({\varepsilon})\) by uniform continuity of \(f\) to guarantee \begin{align*} {\left\lvert {y_1 - y_2} \right\rvert} \leq \delta_1 \implies {\left\lvert {f(y_1) - f(y_2) } \right\rvert} < {\varepsilon}\, \forall y_1, y_2\in X .\end{align*} Now by uniform convergence of \(\left\{{g_n}\right\}\), choose \(N_0 = N_0(\delta_1)\) such that \begin{align*} i, j \geq N_0 \implies {\left\lvert { g_i(x) - g_j(x) } \right\rvert} < \delta_1 \, \forall x\in X .\end{align*}
Now writing \(y_1 \coloneqq g_i(x), y_2 \coloneqq g_j(x)\), choose \(i, j > N_0\) yields \begin{align*} {\left\lvert {y_1 - y_2} \right\rvert} \coloneqq{\left\lvert {g_i(x) - g_j(x) } \right\rvert} < \delta_1 \\ \implies {\left\lvert {f(y_1) - f(y_2)} \right\rvert} \coloneqq{\left\lvert {f(g_i(x)) - f(g_j(x))} \right\rvert} < {\varepsilon} ,\end{align*} and taking the supremum over \(x\in X\) preserves the inequality since \(\delta_1\) and consequently \(N_0\) only depend on \({\varepsilon}\).
Uniform differentiability #complex/qual/completed
Let \(f\) be differentiable on \([a, b]\). Say that \(f\) is uniformly differentiable iff
\begin{align*} \forall \varepsilon > 0,\, \exists \delta > 0 \text{ such that } \quad {\left\lvert {x-y} \right\rvert} < \delta \implies {\left\lvert { {f(x) - f(y) \over x-y} - f'(y)} \right\rvert} < {\varepsilon} .\end{align*}
Prove that \(f\) is uniformly differentiable on \([a, b] \iff f'\) is continuous on \([a, b]\).
\(\implies\): Fix \({\varepsilon}>0\) and choose \(\delta = \delta({\varepsilon})\) to get a bound corresponding to \({\varepsilon}/2\), then for all \(x,y\) with \({\left\lvert {x-y} \right\rvert} < \delta\) on \([a, b]\), we have \begin{align*} {\left\lvert {f'(x) - f'(y) } \right\rvert} \leq {\left\lvert {f'(x) - {f(x) - f(y) \over x- y} } \right\rvert} + {\left\lvert { {f(x) - f(y) \over x-y} - f'(y)} \right\rvert} < {\varepsilon} .\end{align*} This uses uniformity to bound by \({\varepsilon}/2\) the terms involving \(f'(x)\) and \(f'(y)\) respectively. So \(f'\) is in fact uniformly continuous on \([a, b]\).
\(\impliedby\): Let \({\varepsilon}> 0\) and \(x,y\in [a, b]\) be arbitrary. Then by the MVT, we can a \(\xi\in [x, y]\) with \(f'(\xi)(x-y) = f(x) - f(y)\). Then use continuity of \(f'\) to choose \(\delta = \delta({\varepsilon}, x, y)\) so that \({\left\lvert {x-y} \right\rvert} < \delta \implies {\left\lvert {f(x) - f(y)} \right\rvert} < {\varepsilon}\), and note that \({\left\lvert {x-\xi} \right\rvert} \leq {\left\lvert {x-y} \right\rvert} < \delta\), so \begin{align*} {\left\lvert { {f(x) - f(y) \over x-y } - f'(y) } \right\rvert} = {\left\lvert { f'(\xi) - f'(y)} \right\rvert} < {\varepsilon} .\end{align*}
Inf distance #complex/qual/completed
Suppose \(A, B \subseteq {\mathbf{R}}^n\) are disjoint and compact. Prove that there exist \(a\in A, b\in B\) such that \begin{align*} {\left\lVert {a - b} \right\rVert} = \inf\left\{{{\left\lVert {x-y} \right\rVert} {~\mathrel{\Big\vert}~}x\in A,\, y\in B}\right\} .\end{align*}
Define a function \begin{align*} d: A \times B &\to {\mathbf{R}}\\ (x, y) &\mapsto {\left\lVert {x- y} \right\rVert} .\end{align*} Then \(d\) is a continuous function on a compact topological space (where the product is compact by Tychonoff), and the extreme value theorem applies: \(d\) attains its min/max for some pair \((a, b)\) in its domain.
Note that disjointness just guarantees that \({\left\lVert {a-b} \right\rVert}>0\), since \({\left\lVert {a-b} \right\rVert} = 0 \implies a=b\) and \(A \cap B = \emptyset\).
Connectedness #complex/qual/completed
Suppose \(A, B\subseteq {\mathbf{R}}^n\) are connected and not disjoint. Prove that \(A\cup B\) is also connected.
Use that \(X\) is connected iff \(\mathop{\mathrm{Hom}}_{{\mathsf{Top}}}(X, S^0) = \left\{{c_{-1}, c_1}\right\}\), i.e. every continuous map from \(X\to \left\{{-1, 1}\right\}\) is a constant map \(x \xrightarrow{c_{-1}} -1\) or \(x \xrightarrow{c_1} 1\). Let \(f: A\cup B \to S^0\) be arbitrary, and let \(f_1 \coloneqq{ \left.{{f}} \right|_{{A}} }\) and \(f_2 \coloneqq{ \left.{{f}} \right|_{{B}} }\). By connectedness of \(A\), \(f_1\) is a constant map, as is \(f_2\). On the intersection, for \(x\in A \cap B \neq \emptyset\), we have \(f_1(x) = f_2(x)\) since \(x\in A\) and \(x\in B\). So \(f_1\) and \(f_2\) are constant functions that must map to the same constant, so \(f\) is constant and this \(A\cup B\) is connected.
Pointwise and uniform convergence #complex/qual/completed
Suppose \(\left\{{f_n}\right\}_{n\in {\mathbb{N}}}\) is a sequence of continuous functions \(f_n: [0, 1]\to {\mathbf{R}}\) such that \begin{align*} f_n(x) \geq f_{n+1}(x) \geq 0 \quad \forall n\in {\mathbb{N}},\, \forall x\in [0, 1] .\end{align*} Prove that if \(\left\{{f_n}\right\}\) converges pointwise to \(0\) on \([0, 1]\) then it converges to \(0\) uniformly on \([0, 1]\).
Let \({\varepsilon}>0\), we want to show that there exists an \(N_0\) such that \(n\geq N_0\) implies \({\left\lVert {f_n} \right\rVert}_\infty<{\varepsilon}\). Fix \(x\), by pointwise convergence pick \(M_x = M_x(x, {\varepsilon})\) so that \(n\geq M \implies {\left\lvert {f_n(x)} \right\rvert} < {\varepsilon}\). By continuity, this bound holds in some neighborhood \(U_x \ni x\). Produce a cover \(\left\{{U_x}\right\}_{x\in [0, 1]}\rightrightarrows[0, 1]\); by compactness produce a finite subcover \(\left\{{U_1, \cdots, U_m}\right\} \rightrightarrows[0, 1]\). Each \(U_i\) corresponds to some \(x_i\) and some \(M_{x_i}\), so choose \(N_0 > \max_{i\leq m} \left\{{M_{x_i}}\right\}\). Then \(n\geq N_0 \implies N\geq M_{x_i}\) for each \(i\), so \({\left\lvert {f_n(x)} \right\rvert} < {\varepsilon}\) for each \(x\in [0, 1]\) since \(x\in U_i\) for some \(i\). So \(\sup_{x\in X} {\left\lvert {f_n(x)} \right\rvert} = {\left\lVert {f_n} \right\rVert}_{\infty } < {\varepsilon}\).
#complex/qual/work
Show that if \(E\subset [0, 1]\) is uncountable, then there is some \(t\in {\mathbf{R}}\) such that \(E\cap(-\infty ,t)\) and \(E\cap(t, \infty)\) are also uncountable.
See 3.2.12 of Understanding analysis 2ed. of Abbott. Show something stronger, that the following set is nonempty and open: \begin{align*} S \coloneqq\left\{{t\in {\mathbf{R}}{~\mathrel{\Big\vert}~}E \cap(-\infty, t), E \cap(t, \infty) \text{ are uncountable}}\right\} \subseteq {\mathbf{R}} .\end{align*} Write \begin{align*} S_- &\coloneqq\left\{{ t\in {\mathbf{R}}{~\mathrel{\Big\vert}~}E \cap(- \infty, t) \text{ is countable}}\right\} \\ S_+ &\coloneqq\left\{{ s\in {\mathbf{R}}{~\mathrel{\Big\vert}~}E \cap(s, \infty) \text{ is countable}}\right\} .\end{align*}
Note that \(S_- \neq {\mathbf{R}}\) since then we could write \(E = \bigcup_{n\in {\mathbf{Z}}} E \cap(- \infty, n)\) as a countable union of countable sets.
Claim: \(S = (\sup S_-,, \inf S_+)\).
???
#complex/qual/work
Suppose \(f, g: [0, 1] \to {\mathbf{R}}\) where \(f\) is Riemann integrable and for \(x, y\in [0, 1]\), \begin{align*} {\left\lvert {g(x) - g(y)} \right\rvert} \leq {\left\lvert {f(x) - f(y)} \right\rvert} .\end{align*}
Prove that \(g\) is Riemann integrable.
Write \(U(f), L(f)\) for the upper and lower sums of \(f\), so for \(\Pi\) the collection of all partitions of \([0, 1]\), \begin{align*} U(f) \coloneqq\inf_{P\in \Pi} U(f, P) && U(f, P) \coloneqq\sum_{k=1}^n \sup_{x\in I_k}f(x) \cdot \mu(I_k) \\ L(f) \coloneqq\sup_{P\in \Pi} L(f, P) && L(f, P) \coloneqq\sum_{k=1}^n \inf_{x\in I_k} f(x) \cdot \mu(I_k) .\end{align*}
Note that integrability of \(f\) is equivalent to \begin{align*} \forall {\varepsilon}\exists P \text{ such that } U(f, P) - L(f, P) < {\varepsilon}\\ \iff \sum_{k=1}^n \qty{ \sup_{x\in I_k} f(x) - \inf_{x\in I_k} f(x)} \mu(I_k) < {\varepsilon} .\end{align*}
Exercises
Show that \(f(x) = x^n\) is uniformly continuous on any interval \([-M, M]\).
\begin{align*} {\left\lvert {x^n - y^n} \right\rvert} = {\left\lvert {y-x} \right\rvert}{\left\lvert {\sum_{1\leq k \leq n} x^k y^{n-k}} \right\rvert} \leq n M^{n-1}{\left\lvert {y-x} \right\rvert} \overset{y\to x}\longrightarrow 0 .\end{align*}
Show \(f(x) = x^{-n}\) for \(n\in {\mathbf{Z}}_{\geq 0}\) is uniformly continuous on \([0, \infty)\).
\begin{align*} x^{1\over n} - y^{1\over n} \leq (x-y)^{1\over n} \overset{x\to y}\longrightarrow 0 ,\end{align*} using \((a+b)^m \geq a^m + b^m\)
Show that \(f'\) bounded implies \(f\) is uniformly continuous.
Apply the MVT: \begin{align*} {\left\lvert {f(x) - f(y)} \right\rvert} = {\left\lvert {f(\xi)} \right\rvert} {\left\lvert {x-y} \right\rvert} \overset{y\to x}\longrightarrow 0 .\end{align*}
Show that the Dirichlet function \(f(x) = \chi_{I \cap{\mathbf{Q}}}\) is not Riemann integrable and is everywhere discontinuous.
Check \(\sup f = 1\) and \(\inf f = 0\) on every sub-interval, so \(L(f, P) = 0\) and \(U(f, P) = 1\) for every partition \(P\) of \([0, 1]\).
Discontinuity: #todo