Rouché’s Theorem

Write \(f(z) = \sum_{k\leq n} c_k z^k\). Big: \(M(z) = c_nz^n\). Small: \(m(z) = f(z) - M(z) = \sum_{k\leq n-1} c_k z^k\).

Now use that \begin{align*} {\left\lvert {m(z) \over M(z)} \right\rvert} &\coloneqq{\left\lvert {c_n^{-1}\sum_{k\leq n-1} c_k z^{k-n}} \right\rvert} \\ &= {\left\lvert {c_n^{-1}\qty{ {c_1\over z^n} + {c_2\over z^{n-1} } + \cdots + {c_{n-1}\over z} }} \right\rvert} \\ &\overset{{\left\lvert {z} \right\rvert}\to\infty}\longrightarrow 0 ,\end{align*} so choose \(R\) large enough such that for \({\left\lvert {z} \right\rvert} \geq R\), \({\left\lvert {M(z)\over m(z)} \right\rvert} < 1\). Then on \({\left\lvert {z} \right\rvert} = R\), \begin{align*} {\left\lvert {m(z) \over M(z)} \right\rvert} < 1 \implies {\left\lvert {m(z)} \right\rvert} < {\left\lvert {M(z)} \right\rvert} \implies {\sharp}n = {\sharp}Z_{M} = {\sharp}Z_{M+m} = {\sharp}Z_{f} ,\end{align*} since \(c_n z^n\) has \(z=0\) as a root with multiplicity \(n\).

An estimate: write \(f(z) = \sum_{k\leq n} c_k z^k\) with \(c_n = 1\), then for \(R> 1\), on \({\left\lvert {z} \right\rvert} = R\) we have \begin{align*} {\left\lvert {f(z) - z^n} \right\rvert} &\leq \sum_{k\leq n-1} {\left\lvert { c_k z^k} \right\rvert} \\ &\leq \sum_{k\leq n-1} {\left\lvert { c_k} \right\rvert} R^k \\ &\leq \sum_{k\leq n-1} {\left\lvert { c_k} \right\rvert} R^{n-1} \\ &= R^{n-1} \sum_{k\leq n-1} {\left\lvert { c_k} \right\rvert} \\ &\coloneqq R^{n-1} C \\ &\leq R^n \\ &= {\left\lvert {z^n} \right\rvert} ,\end{align*} provided we can choose \(C<R\), but this is possible since \(\sum_{k\leq n-1}{\left\lvert {c_k} \right\rvert}\) is a constant. So \(n = {\sharp}Z_{z^n} = {\sharp}Z_f\).

On \({\left\lvert {z} \right\rvert} \leq 1\):

• Big: \(M(z) = -6z\)
• Small: \(m(z) = z^4 + 3\)

Then on \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}^4 + 3 = 4 < 6 = {\left\lvert {-6z} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(1 = Z_M = Z_f\) here.

On \({\left\lvert {z} \right\rvert} \leq 2\):

• Big: \(M(z) = z^4\)
• Small: \(m(z) = -6z+3\).

Then on \({\left\lvert {z} \right\rvert} = 2\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {-6z + 3} \right\rvert} \leq 6{\left\lvert {z} \right\rvert} + 3 = 15 < 16 = 2^4 = {\left\lvert {z} \right\rvert}^4 = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(4 = Z_M = Z_f\) here.

Thus there are \(4-1 = 3\) zeros in \(1 \leq {\left\lvert {z} \right\rvert} \leq 2\).

On \({\left\lvert {z} \right\rvert} \leq 1\):

• Big: \(M(z) = 12\)
• Small: \(m(z) = z^6 - 5z^3\)

For \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} \coloneqq{\left\lvert {z^7-5z^3} \right\rvert}\leq {\left\lvert {z} \right\rvert}^7 + 5{\left\lvert {z} \right\rvert}^3 = 6 < 12 \coloneqq{\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(0 = Z_M = Z_{f}\).

On \({\left\lvert {z} \right\rvert} \leq 2\),

• Big: \(M(z) = z^7\)
• Small: \(m(z) = -5z^3 + 12\)

On \({\left\lvert {z} \right\rvert} = 2\), \begin{align*} {\left\lvert {m(z)} \right\rvert} \coloneqq{\left\lvert {-5z^3 + 12} \right\rvert} \leq 5{\left\lvert {z} \right\rvert}^2 + 12 = 32 < 128 = 2^7 \coloneqq{\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(7 = Z_M = Z_{f}\).

So \(f\) has 7 zeros in \(1 \leq {\left\lvert {z} \right\rvert} \leq 2\).

On \({\left\lvert {z} \right\rvert} < 1\):

• Small: \(m(z) = z^4+3\)
• Big: \(M(z) = -6z\)

On \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {z^4+3} \right\rvert} \leq {\left\lvert {z} \right\rvert}^4 + 3 = 4 < 6 = {\left\lvert {-6z} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(Z_f = Z_M = 1\).

On \({\left\lvert {z} \right\rvert} < 2\):

• Small: \(-6z+3\)
• Big: \(z^4\)

On \({\left\lvert {z} \right\rvert} = 2\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = \leq 6 + 3 = 9 < 2^4 = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(Z_f = Z_M = 4\).

Thus there are \(4-1=3\) zeros in \(1 \leq {\left\lvert {z} \right\rvert} \leq 2\).

Big: \(M(z) = -4z^3\). Small: \(m(z) = z^7 - 1\). Then on \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {z^7-1} \right\rvert} \leq {\left\lvert {z} \right\rvert}^7 + 1 = 2 < 4 = {\left\lvert {-4z^4} \right\rvert} ,\end{align*} so \(f\) and \(M\) have the same number of zeros: three.

Big: \(M(z) = 4\) Small: \(m(z) = z^3 + 2z\). On \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}^3 + 2{\left\lvert {z} \right\rvert} = 1+2=3 < 4 = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(0 = Z_M = Z_{M+m} = Z_f\) in \({\mathbb{D}}\).

Big: \(M(z) = 3z^2\). Small: \(m(z) = z^3+bz + b^2\). Then on \({\left\lvert {z} \right\rvert} = 1\): \begin{align*} {\left\lvert {m(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}^3 + b{\left\lvert {z} \right\rvert} + b^2 = 1 + b + b^2 < 3 = {\left\lvert {M(z)} \right\rvert} ,\end{align*} and \(M(z)\) has exact two roots in \({\mathbb{D}}\).

Key observation: \begin{align*} P_n(z) = \sum_{1\leq k\leq n-1} kz^{k-1} = {\frac{\partial }{\partial z}\,}Q_n(z) \qquad Q(z) \coloneqq\sum_{0\leq k \leq n} z^k .\end{align*} Note that \(Q(z) \to \sum_{k\geq 0} z^k = {1\over 1-z}\) uniformly on \({\left\lvert {z} \right\rvert} \leq R < 1\) since this power series has radius of convergence 1. Similarly \(P_n(z)\) converges uniformly to \({\frac{\partial }{\partial z}\,}{1\over 1-z} = {1\over (1-z)^2}\), so let \(P(z) \coloneqq{1\over (1-z)^2}\). Note that \(P\) is nonvanishing in \({\mathbb{D}}\).

Strategy:

• Small: \(m(z) = P(z) - P_n(z)\), look for an upper bound \({\left\lvert {m(z)} \right\rvert} < U\)
• Big: \(P(z)\), look for a lower bound \(L\) with \({\left\lvert {P(z)} \right\rvert} > L > U\).

Just by considering the geometry of circles of radius \(R < 1\) and \(1\) and measuring distances to the point \(1\), we can estimate \begin{align*} 0 < 1-R \leq {\left\lvert {1-z} \right\rvert} < 1+R < 2 \implies {\left\lvert {P(z)} \right\rvert} = {1\over {\left\lvert {1-z} \right\rvert}^2} \geq {1\over 2^2} = {1\over 4} .\end{align*}

Now fix \({\varepsilon}< {1\over 4}\) and use uniform convergence of \(P_n\to P\) to produce an \(N\) such that \(n\geq N\) implies \({\left\lVert {P-P_n} \right\rVert}_\infty < {\varepsilon}\) in \({\left\lvert {z} \right\rvert} \leq R\). Then on \({\left\lvert {z} \right\rvert} = R\), for \(n\geq N\), \begin{align*} {\left\lvert {m(z)} \right\rvert} \coloneqq{\left\lvert {P(z) - P_n(z)} \right\rvert} \leq {\left\lVert {P - P_n} \right\rVert}_\infty < {\varepsilon}< {1\over 4} \leq {\left\lvert {P(z)} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(0 = Z_P = Z_{P_n}\) by Rouché.

Write \(f(z) \coloneqq 6z^3 + 1 + e^z\).

• Small: \(m(z) = e^z + 1\)
• Large: \(M(z) = 6z^3\)
• The estimate: \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {e^z + 1} \right\rvert} \leq e^{\Re(z)} + 1 \leq e^{{\left\lvert {z} \right\rvert}} + 1 = e+1 < 6 = {\left\lvert {6z^3} \right\rvert} ,\end{align*} so \(3 = Z_M = Z_f\).

• Small: \(m(z) = z^6-3\)
• Big: \(M(z) = 4z^2 e^{z+1}\), which has two such zeros

Now estimate \(m\) from above: \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {z^6 - 3} \right\rvert} \leq {\left\lvert {z} \right\rvert}^6 + 3 = 4 .\end{align*} and \(M\) from below: \begin{align*} {\left\lvert {M(z)} \right\rvert} = {\left\lvert {4z^2 e^{z+1}} \right\rvert} = 4e{\left\lvert {z} \right\rvert}^4 e^{\Re(z)} = 4e e^{\Re(z)} \geq 4e e^{-1} = 4 ,\end{align*} which unfortunately isn’t quite enough. But equality occurs iff \(\Re(z) = -1\) on \(S^1\), so \(z=-1\), in which case \({\left\lvert {m(-1)} \right\rvert} = {\left\lvert {1-3} \right\rvert} = 2\), so the inequality is in fact strict. So \(2 = Z_M = Z_f\).

Take a contour \(\gamma_1 \coloneqq\left\{{it {~\mathrel{\Big\vert}~}t\in {\mathbf{R}}}\right\}\) and \(\gamma_2\coloneqq\left\{{Re^{it} {~\mathrel{\Big\vert}~}t\in [-\pi, \pi]}\right\}\).

• Big: \(M(z) = z^3 + 1\)
• Small: \(m(z) = -z\)

On \(\gamma_2\), we have \({\left\lvert {z} \right\rvert} = R\), so take \(R\) large enough that the following estimate holds: \begin{align*} {\left\lvert {M(z)} \right\rvert} = {\left\lvert {z^3 + 1} \right\rvert} \geq {\left\lvert { {\left\lvert {z} \right\rvert}^3 - 1} \right\rvert} = R^3 - 1 > R = {\left\lvert {m(z)} \right\rvert} = R .\end{align*} In particular, this works for \(R> 1\).

On \(\gamma_1\), note

• \({\left\lvert {M(z)} \right\rvert} = {\left\lvert { (it)^3 + 1 } \right\rvert} = {\left\lvert {1-it^3} \right\rvert}\)
• \({\left\lvert {m(z)} \right\rvert} = {\left\lvert {it} \right\rvert}\)

These can be interpreted geometrically: the former is the hypotenuse of a triangle and the latter is a leg, so \({\left\lvert {M(z)} \right\rvert} \geq {\left\lvert {m(z)} \right\rvert}\) will hold:

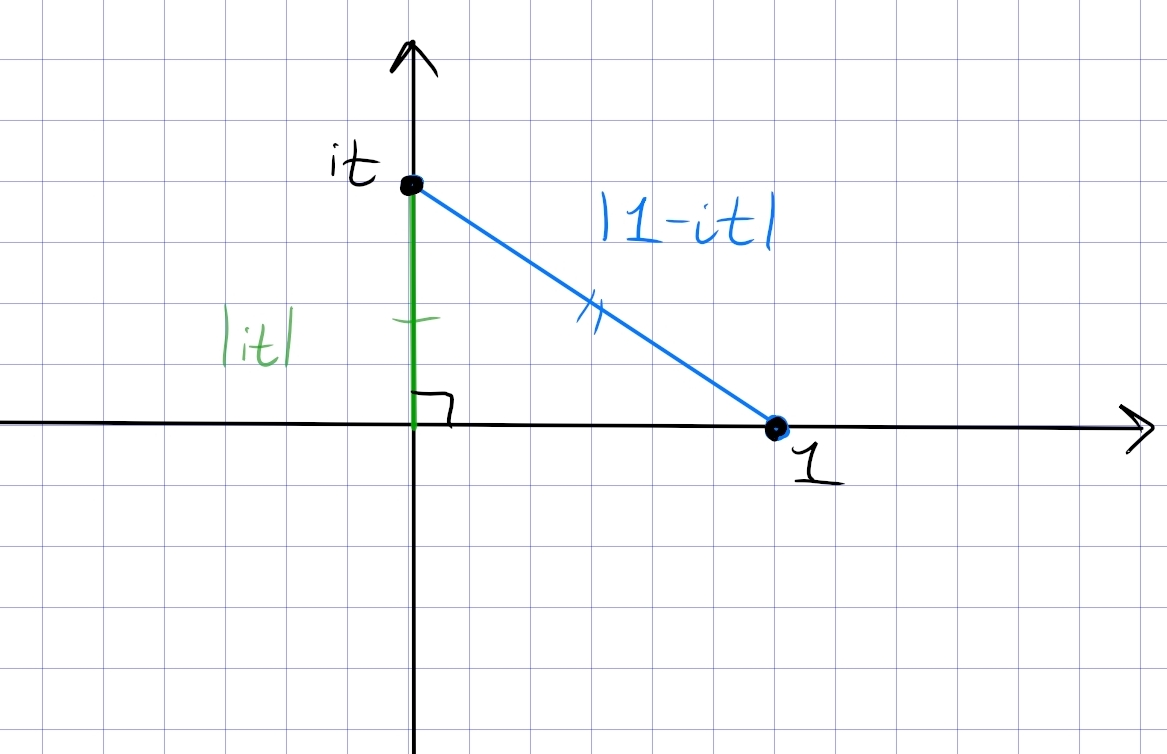
Now note that \(z^3 + 1\) has roots \(\omega_3, \omega_3^2, \omega_3^3=-1\) for \(\omega_k \coloneqq e^{i\pi\over k}\), and the first two are in the right half-plane. So \(2 = {\sharp}Z_M = {\sharp}Z_f\) by Rouché.

For the \(n=1\) case, \(f_1(z) = 0 \iff 1+z = 0 \iff z=-1\), so this has no roots in \({\mathbb{D}}\). For \(n=2\), factor \begin{align*} f_2(z) = 1 + z + z^2 = (z-\zeta_3^2)(z-\zeta_3^{-2}) ,\end{align*} using that \begin{align*} \zeta_3^2\cdot \zeta_3^{-2} = 1,\qquad -(\zeta_3^2 + \zeta_3^{-2}) = -2\Re(\zeta_3^2) = -2\cos\qty{2\pi \over 3} = 1 .\end{align*} Now use that \({\left\lvert {\zeta_3^{k}} \right\rvert} = 1\), which is not in \({\mathbb{D}}\).

For \(n\geq 3\): toward applying Rouche’s theorem, let \(M(z) = 1 + z\) and \(m(z) = {1\over 2}z^2 + \cdots + {1\over n!}z^n\). Note that on \({\left\lvert {z} \right\rvert} = 1\), \({\left\lvert {m(z)} \right\rvert} = 2\), and \begin{align*} {\left\lvert {m(z)} \right\rvert} &= {\left\lvert {\sum_{k\geq n+1} {z^k\over k!} } \right\rvert} \\ &\leq \sum_{k\geq n+1} { {\left\lvert {z} \right\rvert}^k \over k!} \\ &\leq \sum_{k\geq n+1} { 1 \over k!} \\ &= e^1 - \sum_{k\leq n} {1\over k!} .\end{align*} Suppose \(n\geq 3\), \begin{align*} {\left\lvert {m(z)} \right\rvert} < e - (1 + 1 + \cdots) \approx 0.718 < 2 ,\end{align*} then Rouché applies directly and \begin{align*} 0 = {\sharp}Z_M({\mathbb{D}}) ={\sharp}Z_{M+m}({\mathbb{D}}) \coloneqq{\sharp}Z_f({\mathbb{D}}) ,\end{align*} noting that \(M(z) = 0 \iff z= -1\), which isn’t contained in the open disc \({\mathbb{D}}\).

Note that \({\left\lvert {e^z} \right\rvert} = e^{\Re(z)}\), which is maximizes on \(S^1\) at \(z=1 \in {\mathbf{R}}\) and minimized at \(z=-1\). Write \(f(z) = e^z-az^n\), so solution correspond to zeros of \(f\).

Case 1: suppose \({\left\lvert {a} \right\rvert} > e\). Big: \(M(z) = az^n\). Small: \(m(z) = e^z\). On \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {e^z} \right\rvert} = e^\Re(z) \leq e^1 < {\left\lvert {a} \right\rvert} = {\left\lvert {az^n} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(f\) has \({\sharp}Z_M = n\) zeros.

Case 2: suppose \({\left\lvert {a} \right\rvert} < 1/e\). Big: \(M(z) = e^z\). Small: \(m(z) = az^n\). On \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {az^n} \right\rvert} = {\left\lvert {a} \right\rvert} < e^{-1}\leq e^{\Re(z)} = {\left\lvert {e^z} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} and \(M\) has no zeros in \({\mathbb{D}}\) (and in fact none in \({\mathbf{C}}\)), so neither does \(f\).

More is true: this will hold for any disc of arbitrary radius \(R\), with \(n\) depending on \(R\). Fix \(R\), then use that \(P_n(z) \overset{n\to\infty}\longrightarrow e^z\) uniformly on the compact disc \({\left\lvert {z} \right\rvert} \leq R\). Consequently, setting \(g_n(z) \coloneqq{P_n(z)\over e^z}\), we have \(g_n(z) \to 1\) uniformly on this disc, for any \({\varepsilon}> 0\) this can be used to produce an \(n\gg 1\) such that \({\left\lvert { g_n(z) - 1 } \right\rvert} < {\varepsilon}\) for all \({\left\lvert {z} \right\rvert} \leq R\).

So take \({\varepsilon}\coloneqq 1\) and define \(h(z) \coloneqq 1\), then for \({\left\lvert {z} \right\rvert} = R\) \begin{align*} {\left\lvert {g_n(z) - 1} \right\rvert} < 1 = {\left\lvert {h(z)} \right\rvert} ,\end{align*} so by Rouché, \begin{align*} 0 = {\sharp}Z_{h} = {\sharp}Z_{h + (g_n - 1)} = {\sharp}Z_{g_n} ,\end{align*} since \(h\) has no zeros at all. Take \(R=10\) to get the stated result.

For \(P_n(z) - 1\), note that \(e^z-1=0\) has three solutions in \({\left\lvert {z} \right\rvert} < 10\), namely \(z=0, \pm 2\pi i\). We similarly have \(P_n(z)-1\to e^z-1\) uniformly, so on a disc of radius \(R\) choose \(n\) large enough so that \begin{align*} {\left\lvert {{P_n(z) -1 \over e^z - 1} - 1} \right\rvert} &< 1 \\ \implies {\left\lvert { (P_n(z) - 1) - (e^z-1) \over e^z-1} \right\rvert} &< 1 \\ \implies {\left\lvert { (P_n(z) - 1) - (e^z-1)} \right\rvert} &< {\left\lvert {e^z-1} \right\rvert} \\ \coloneqq{\left\lvert {m(z)} \right\rvert} &< {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \begin{align*} 3 = {\sharp}Z_M = {\sharp}Z_{M+m} = {\sharp}Z_{P_n - 1} .\end{align*}

Write \(p(z) \coloneqq a_0 + \cdots + z^n\). Toward a contradiction, suppose not so that \({\left\lvert {p(z)} \right\rvert} < 1\) on \({\left\lvert {z} \right\rvert} = 1\). Then \begin{align*} {\left\lvert {f(z)} \right\rvert} < 1 = {\left\lvert {z} \right\rvert}^n \qquad \text{ on } {\left\lvert {z} \right\rvert} = 1 .\end{align*} Taking \(m(z) \coloneqq f(z)\) and \(M(z) \coloneqq-z^n\), we have \begin{align*} n = {\sharp}Z_M = {\sharp}Z_{M+m} = {\sharp}Z_{f(z) - z^n} \leq n-1 ,\end{align*} since \(f(z) - z^n\) is degree at most \(n-1\), a contradiction.

The boundary region is \(\left\{{1+it{~\mathrel{\Big\vert}~}t\in {\mathbf{R}}}\right\}\), write \(g(z) = ce^z-z\) so that fixed points of \(f\) are zeros of \(g\).

Big: \(M(z) = z\). Small: \(m(z) = ce^z\). Then for \(z=1+it\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {c} \right\rvert}e^{\Re(z)} < ce < 1 \leq \sqrt{1^2+t^2} = {\left\lvert {1+it} \right\rvert} = {\left\lvert {z} \right\rvert} ,\end{align*} so \(M\) and \(g\) have the same number of zeros, and \(M\) has a unique zero.

Consider \(f(z) \coloneqq z\sin(z) - a\).

Big: \(M(z) \coloneqq z\sin(z)\). Small: \(m(z) \coloneqq-a\).

Use the following estimate:

\begin{align*} {\left\lvert {z\sin(z)} \right\rvert}^2 &= {\left\lvert {z\over 2} \right\rvert}^2 {\left\lvert {e^{iz} - e^{-iz}} \right\rvert}^2 \\ &\geq {\left\lvert {z\over 2} \right\rvert}^2 {\left\lvert { {\left\lvert {e} \right\rvert}^{iz} } \right\rvert} - {\left\lvert { e^{-iz} } \right\rvert} ^2 \\ &= {\left\lvert {z\over 2} \right\rvert}^2 {\left\lvert {e^{-\Im(z)} - e^{\Im(z)} } \right\rvert} \\ &\overset{\Im(z)\to\infty}\longrightarrow \infty ,\end{align*} and so in particular a radius \(R\) can be chosen large enough so that \({\left\lvert {z\sin(z)} \right\rvert} > a\) for any \(a\). Thus for \({\left\lvert {z} \right\rvert} = R\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {a} \right\rvert} \leq {\left\lvert {z\sin(z)} \right\rvert} < {\left\lvert {M(z)} \right\rvert} \implies {\sharp}Z_{M} = {\sharp}Z_{M+m} = {\sharp}Z_f .\end{align*} To count the number of zeros of \(z\sin(z)\), note that this equals zero at \(z=0\) with multiplicity two and \(z= k\pi\) for \(k\in {\mathbf{Z}}\). Choosing \(R = {\pi \over 2} + n\pi\) for \(n\) large enough, there are exactly \(2n+2\) such zeros (with multiplicity) to \(z\sin(z)\), and thus \(2n+2\) zeros to \(z\sin(z) - a\). Now using that \(z\sin(z) - a\) has exactly \(2n+2\) real roots (??), this must be all of them.

Unsure how to find any roots of this thing, real or not!

The key step: getting the following inequality to work \begin{align*} {\left\lvert {az^n} \right\rvert} = {\left\lvert {a} \right\rvert}{\left\lvert {z} \right\rvert}^n < c \leq 1 = {\left\lvert { {\left\lvert {z} \right\rvert} - {\left\lvert {1} \right\rvert} } \right\rvert} \leq {\left\lvert {z+1} \right\rvert} .\end{align*} If this is true, then \(1 = {\sharp}Z_{z+1} = {\sharp}Z_f\). If \({\left\lvert {a} \right\rvert} < 2^n\), this holds because \({\left\lvert {a} \right\rvert}{\left\lvert {z} \right\rvert}^n < {1\over 2^n} 2^n = 1\), so taking \(c\coloneqq 1\) works.

Otherwise, suppose \({\left\lvert {a} \right\rvert} \geq 2^n\). Letting \(z_k\) be the roots of \(f\) and considering the constant coefficient, we have \begin{align*} a\prod_{k\leq n} z_k = 1 \implies {\left\lvert { \prod_{k\leq n} z_k } \right\rvert} = {\left\lvert {1\over a} \right\rvert} \leq 2^n ,\end{align*} so not every \(z_k\) can satisfy \({\left\lvert {z_k} \right\rvert} > 2\) and at least one is in \({\left\lvert {z} \right\rvert} \leq 2\).