Open Mapping, Riemann Mapping, Casorati-Weierstrass

Idea:

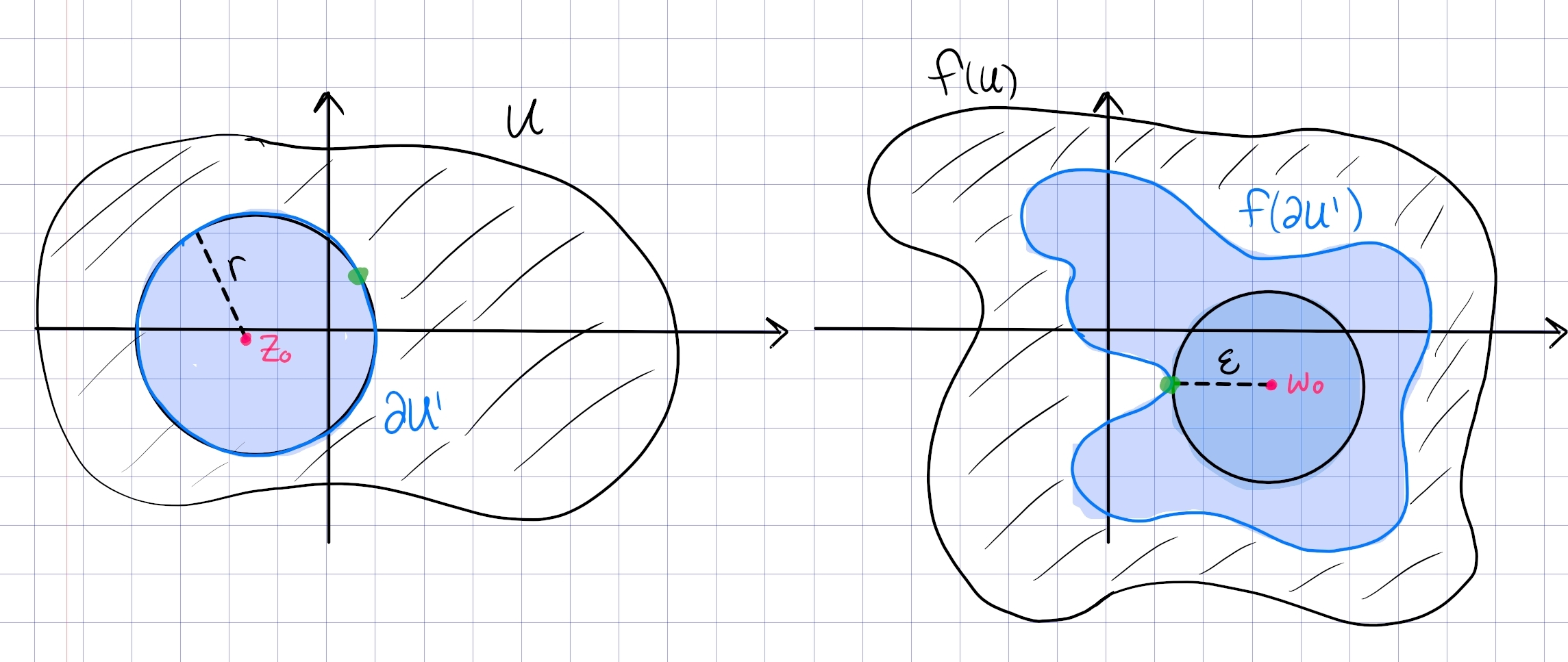
Let $f: U\to {\mathbf{C}}$. Pick $w_0\in W$ with $f(z_0) = w_0$ for some $z_0\in U$; we want to show that $w_0$ is an interior point of $f(U)$, so we’re looking for a disc containing $w_0$ and contained in $f(U)$.

Write $$\begin{align*} g_0(z) \coloneqq f(z) - w_0 ,\end{align*}$$ so $g_0$ is holomorphic and has a zero at $z_0$. Since zeros of holomorphic functions are isolated, there is some $U' \coloneqq{\mathbb{D}}_r(z_0)$ where $g_0$ is nonvanishing. The claim is that if we choose ${\varepsilon}$ small enough, we can arrange so that $W_{\varepsilon}\coloneqq{\mathbb{D}}_{\varepsilon}(w_0) \subseteq f(U)$. This will follow if for every $w\in W_{\varepsilon}$, the equation $f(z) = w$ has a solution in $U$, i.e.  Define a function that counts the number of zeros: $$\begin{align*} F(w) &\coloneqq{1\over 2\pi i}\int_{{{\partial}}U' } {f(z) \over f(z) - w_1 }\,dz\\ &= {1\over 2\pi i}\int_{{{\partial}}U' } {{\frac{\partial }{\partial z}\,}\qty{f(z) - w} \over f(z) - w }\,dz\\ &= {\sharp}Z(f(z) - w, U' ) ,\end{align*}$$ which is the number of zeros of $f(z) - w$ in $U'$ by the argument principle. Now $F$ is a ${\mathbf{Z}}{\hbox{-}}$valued function, and the only obstruction to continuity is if $f(z) - w = 0$ in the integrand for some $z$. The claim is that ${\varepsilon}$ can be chosen such $$\begin{align*} z\in {{\partial}}U' \implies {\left\lvert {f(z) - w} \right\rvert} > 0 \qquad \forall w\in W_{\varepsilon} .\end{align*}$$ The theorem then follows immediately: $F(w): U' \to W_{\varepsilon}$ is a continuous and ${\mathbf{Z}}{\hbox{-}}$valued, thus constant. Then noting that $F(w_0) = 1$ since $z_0\in U'$ and $w_0\in W_{\varepsilon}$, we have $F\equiv 1 > 0$ for all $w$.

Note that $f$ is non-constant, since a constant function is extremely non-injective. Consider the singularity at $\infty$:

• If it is removable, then $f$ is bounded outside of a large disc, and bounded inside of it as a continuous function on a compact set, making $f$ entire and bounded and thus constant by Liouville.

• If it is essential, then by Casorati-Weierstrass there is a large disc of radius $R$ such that $f(\overline{{\mathbb{D}}_R}^c) \subseteq {\mathbf{C}}$ is dense. By the open mapping theorem, $f({\mathbb{D}}_R) \subseteq {\mathbf{C}}$ is open, so by density it intersects $f(\overline{{\mathbb{D}}_R}^c)$, but ${\mathbb{D}}_R \cap\overline{{\mathbb{D}}_R}^c$ is empty so this contradicts injectivity.

So we can conclude $\infty$ is a pole of some order $N$, so $f\qty{1\over z} = \sum_{0\leq k\leq N} c_k z^{-k}$ and thus $f(z) = \sum_{0\leq k\leq N} c_k z^k$ is a polynomial of degree $N$. However, a polynomial of degree $N$ is generically $N$-to-one locally, so injectivity forces $N=1$ and $f(z) = c_0 + c_1 z$, where $c_1\neq 0$ since $f$ is nonconstant.

Write $g(z) \coloneqq f(1/z)$, which has a singularity at $z=0$. The claim is that this is a pole.

If $z=0$ is a removable singularity, $g$ is bounded on some closed disc ${\left\lvert {z} \right\rvert} \leq {\varepsilon}$, so $f$ is bounded on ${\left\lvert {z} \right\rvert} > {\varepsilon}$. Moreover $f$ is continuous and ${\left\lvert {z} \right\rvert}\leq {\varepsilon}$, $f$ is bounded on this disc. This makes $f$ an entire bounded function and thus constant by Liouville, contradicting injectivity.

If $z=0$ is essential, then by Casorati-Weierstrass pick a punctured disc $D = \left\{{{\left\lvert {z} \right\rvert} \leq {\varepsilon}}\right\}$ where $g(D)$ is dense in ${\mathbf{C}}$. Writing $D^c \coloneqq\left\{{{\left\lvert {z} \right\rvert} > {\varepsilon}}\right\}$, this means that $f(D^c)$ is dense. But $U\coloneqq\left\{{{\left\lvert {z} \right\rvert} < {\varepsilon}}\right\}$ is open and by the open mapping theorem $f(U)$ is open, so by density there is a point $w\in f(D^c) \cap f(U)$ while $U \cap D^c = \emptyset$, again contradicting injectivity.

So $z=0$ is a pole of $g$, and $g$ admits a Laurent expansion $$\begin{align*} g(z) = \sum_{k\geq -N} c_k z^k .\end{align*}$$ Since $f$ is entire, it equals its Laurent expansion at $z=0$, so equating the two series yields $$\begin{align*} f(z) = \sum_{k\geq 0} d_k z^k &\implies g(z) = \sum_{k\geq 0} {d_k \over z^k} = \sum_{1\leq k\leq N} {c_k\over z^k} + \sum_{k\geq 0} c_k z^k \\ &\implies \sum_{k\geq 0} c_k z^k = 0 \\ &\implies f(z) = \sum_{0\leq k \leq N} c_k z^k ,\end{align*}$$ making $f$ a polynomial of degree at most $N$.

Now $f$ can not be degree zero, since constant maps are not injective. Moreover $f$ can not be degree $N\geq 2$, since any polynomial of degree $N$ has $N$ roots in ${\mathbf{C}}$ by the fundamental theorem of algebra, and any two distinct roots will be points where injectivity fails. Finally, ruling out the case of roots with multiplicity, if $f(z) = c(z-a)^N$, then $f$ has exactly $N$ preimages in a neighborhood of $a$. Letting $p$ be any such point, we can find $N$ complex points mapping to it: $$\begin{align*} p = c(z-a)^N &\implies {p\over c} = (z-a)^N \\ &\implies \qty{p\over c}^{1\over N}\zeta_N^k = z-a \quad k=0,1,\cdots, n-1 \\ &\implies z_k\coloneqq\qty{p\over c}^{1\over N}\zeta_N^k + a \xrightarrow{f} p .\end{align*}$$

So $f$ must be degree exactly 1, i.e. $f(z) = az+b$.

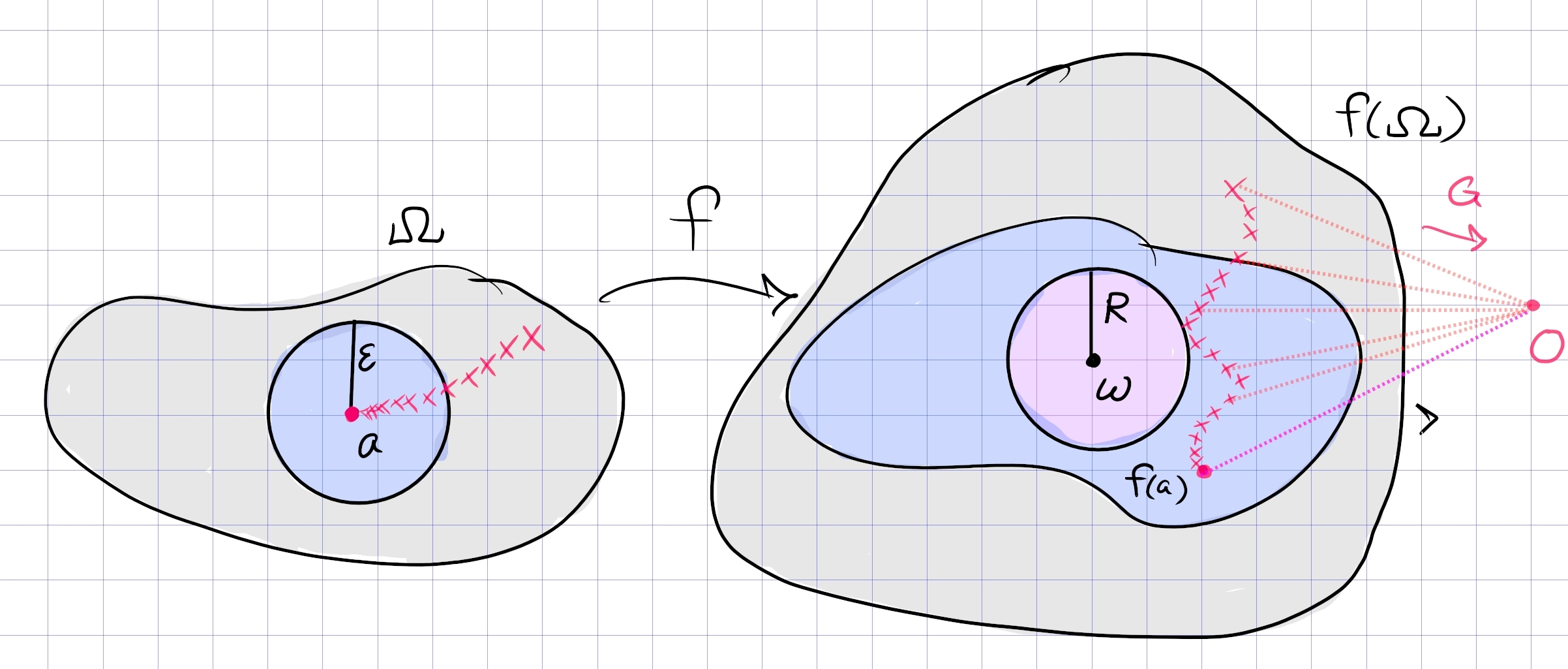
As in the proof of Casorati-Weierstrass, fix $w$ and suppose toward a contradiction that no sequence sequence exists. Then there is some ${\varepsilon}, R$ such that $$\begin{align*} f({\mathbb{D}}_{\varepsilon}(a)) \subseteq {\mathbb{D}}_R(w)^c ,\end{align*}$$ for otherwise one could construct the desired sequence. In particular, ${\left\lvert {f(z) - w} \right\rvert} > R$ for ${\left\lvert {z-a} \right\rvert} < {\varepsilon}$, so define $$\begin{align*} G(z) \coloneqq{1\over f(z) - w} \implies {\left\lvert {G(z)} \right\rvert} \leq R^{-1}< \infty \qquad \text{in }{\mathbb{D}}_{\varepsilon}(a) .\end{align*}$$ Since $G$ is bounded in this disc, any singularities here must be removable. Since the $a_k$ are poles of $f$, they are zeros of $G$ – this is because if ${\left\lvert {f(z)} \right\rvert}\to\infty$ as $z\to a_k$ then ${\left\lvert {G(z)} \right\rvert}\to 0$. So $G(a_k) = 0$ for all $k$ and $G$ extends holomorphically over the removable singularity $a$, and by continuity must satisfies $G(a) = 0$. But now $G$ is zero on a set with a limit point, hence $G\equiv 0$ by the identity principle. This is a contradiction since if $G\equiv 0$ on an open set, $f$ has poles on an open set, contradicting that $f$ is holomorphic on $\Omega$.

The difference to Casorati-Weierstrass: the singularity at $a$ is not essential, since in particular it is not isolated. The conclusion is nearly the same though: this says that every $w\in {\mathbf{C}}$ is a limit point for $f(\Omega)$, so $w$ is in the closure of $f(\Omega)$, making the image dense in ${\mathbf{C}}$.

Ideas:

• If an entire function doesn’t have dense image, it’s constant by Liouville using the proof idea of Casorati-Weierstrass.
• Conjugate $f$ by $T:{\mathbb{H}}\to {\mathbb{D}}$ where $T(z) = {z-i\over z+i}$, then $\tilde f(0) = 0$
• Use that $T({\mathbf{R}}) = S^1$, so ${\left\lvert {\tilde f(z)} \right\rvert} = 1$ when ${\left\lvert {z} \right\rvert} = 1$.
• Schwarz reflection applies to $\tilde f$ to define an entire function – if $f$ isn’t dense, then the extension of $\tilde f$ isn’t dense…?
• No clue how to use $f(i) = i$, although it implies $\tilde f(0) = 0$ and Schwarz applies.