I’d like to thank the following individuals for their contributions to this document:
- Edward Azoff, for supplying a problem sheet broken out by topic.
- Mentzelos Melistas, for explaining and documenting many solutions to these questions.
- Jingzhi Tie, for supplying many additional problems and solutions.
- Swaroop Hegde for supplying a number of proofs
Real Analysis Review
Tie’s Extra Questions: Fall 2015 (Computing area)
Let \(f(z) = \sum_{n=0}^\infty c_n z^n\) be analytic and one-to-one in \(|z| < 1\). For \(0<r<1\), let \(D_r\) be the disk \(|z|<r\). Show that the area of \(f(D_r)\) is finite and is given by \begin{align*} S = \pi \sum_{n=1}^\infty n |c_n|^2 r^{2n} .\end{align*}
Note that in general the area of \(f(D_1)\) is infinite.
Since \(f\) is injective, \(f'\) is nonvanishing in \(\Omega \coloneqq{\left\lvert {z} \right\rvert} \leq r\). A computation: \begin{align*} \mu(f({\mathbb{D}}_r)) &= \int_{{\mathbb{D}}_r} {\left\lvert {f'(z)} \right\rvert}\,dz\\ &= \int_{{\mathbb{D}}_r} f'(z) \mkern 1.5mu\overline{\mkern-1.5muf'(z)\mkern-1.5mu}\mkern 1.5mu \,dz\\ &= \int_{{\mathbb{D}}_r} \qty{\sum_{j\geq 1} jc_j z^{j-1} } \mkern 1.5mu\overline{\mkern-1.5mu \qty{\sum_{k\geq 1} kc_k z^{k-1}}\mkern-1.5mu}\mkern 1.5mu \,dz\\ &= \int_{{\mathbb{D}}_r} \qty{\sum_{j\geq 1} j c_j z^{j-1} } { \qty{\sum_{k\geq 1} k \mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu^{k-1} }} \,dz\\ &= \int_{{\mathbb{D}}_r} \sum_{j, k\geq 1} jk c_j \mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu z^{j-1}\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu^{k-1}\,dz\\ &= \int_0^R\int_0^{2\pi} \sum_{j, k\geq 1} jk c_j \mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu (re^{it})^{j-1} (re^{-it})^{k-1} r\,dr\,dt\\ &= \int_0^R\int_0^{2\pi} \sum_{j, k\geq 1} jk c_j \mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu r^{j+k-1} e^{i(j-k)t} \,dr\,dt\\ &= \int_0^R \sum_{k\geq 1} k^2 {\left\lvert {c_k} \right\rvert}^2 r^{2k-1} \cdot 2\pi \,dt\\ &= \sum_{k\geq 1} k^2 {\left\lvert {c_k} \right\rvert}^2 {r^{2k} \over 2k}\Big|_{r=0}^R \\ &= \pi \sum_{k\geq 1} k {\left\lvert {c_k} \right\rvert}^2 R^{2k} .\end{align*}
Tie’s Extra Questions: Fall 2015 (Variant)
Let \(f(z) = \sum_{n= -\infty}^\infty c_n z^n\) be analytic and one-to-one in \(r_0< |z| < R_0\). For \(r_0<r<R<R_0\), let \(D(r,R)\) be the annulus \(r<|z|<R\). Show that the area of \(f(D(r,R))\) is finite and is given by \begin{align*}S = \pi \sum_{n=- \infty}^\infty n |c_n|^2 (R^{2n} - r^{2n}).\end{align*}
See above solution: all goes identically up until the integral over \(r\) values, just replace \(\int_0^R\) with \(\int_r^R\).
Spring 2019.1
^0a8ca5
Define
\begin{align*} E(z)=e^{x}(\cos y+i \sin y) . \end{align*}
- Show that \(E(z)\) is the unique function analytic on \(\mathbb{C}\) that satisfies
\begin{align*} E^{\prime}(z)=E(z), \quad E(0)=1 . \end{align*}
- Conclude from the first part that \begin{align*} E(z)=\sum_{n=0}^{\infty} \frac{z^{n}}{n !} .\end{align*}
Recurrences
Let \(x_0 = a, x_1 = b\), and set \begin{align*} x_n \coloneqq{x_{n-1} + x_{n-2} \over 2} \quad n\geq 2 .\end{align*}
Show that \(\left\{{x_n}\right\}\) is a Cauchy sequence and find its limit in terms of \(a\) and \(b\).
With some substitution, one can compute \begin{align*} {\left\lvert {x_n - x_{n-1}} \right\rvert} = {\left\lvert {{1\over 2} x_{n-1} + {1\over 2} x_{n-2} - x_{n-1}} \right\rvert} = {1\over 2} {\left\lvert {x_{n-1} - x_{n-2}} \right\rvert} ,\end{align*} which holds for all \(n\). This is enough to show that the sequence is contractive, i.e. \begin{align*} {\left\lvert {x_n - x_{n-1}} \right\rvert} = c {\left\lvert {x_{n-1} - x_{n-2}} \right\rvert} && c\in (0, 1) .\end{align*}
Apply this recursively yields \begin{align*} {\left\lvert {x_n - x_{n-1}} \right\rvert} = \qty{1\over 2}^{n-1} {\left\lvert {b-a} \right\rvert} \overset{n\to\infty}\longrightarrow 0 ,\end{align*} since \({\left\lvert {b-a} \right\rvert}\) is a constant. So in fact \(x_n\) is convergent and thus Cauchy convergent.
Note: to compare \({\left\lvert {x_i - x_j} \right\rvert}\) directly, assume \(i>j\) and apply the above estimate \(i-j+1\) on \({\left\lvert {x_i - x_{i-1}} \right\rvert}, {\left\lvert {x_{i-1} - x_{i-2}} \right\rvert}, \cdots\) to reduce to this case. This yields something like \begin{align*} {\left\lvert {x_i - x_j} \right\rvert} = \qty{1\over 2}^{i-j+1}{\left\lvert {x_{j} - x_{j-1}} \right\rvert} = \qty{1\over 2}^{i-j+1} \qty{1\over 2}^{j-1} {\left\lvert {b-a} \right\rvert}\to 0 .\end{align*} One could equivalently use the triangle inequality and a partial geometric sum to write \begin{align*} {\left\lvert {x_i - x_j} \right\rvert} \leq \sum_{j\leq k \leq i-1} {\left\lvert {x_{k+1} - x_{k}} \right\rvert} \implies {\left\lvert {x_i - x_j} \right\rvert} \leq c^j\qty{1\over 1-c}{\left\lvert {b-a} \right\rvert} .\end{align*}
Computing its limit: the usual trick of setting \(L \coloneqq\lim x_n = \lim x_{n-1} = \lim x_{n-2}\) only yields \(L = {L + L \over 2}\) here, and thus no information. Instead assume \(x_n = r^n\) is geometric, then \begin{align*} 2x_n - x_{n-1} - x_{n-2} = 0 \implies 2r^n - r^{n-1} - r^{n-2} = 0 \implies 2r^2 - r - 1 = 0 \iff (2r+1)(r-1) = 0 \implies r = -1/2, 1 .\end{align*} Write a general solution as \begin{align*} x_n = c_1 (-1/2)^n + c_2 (1)^n = c_1 (-1/2)^n + c_2 ,\end{align*} and solve for initial conditions: \begin{align*} x_0: \quad a &= c_1 + c_2 \\ x_1: \quad b &= (-1/2)c_1 + c_2 \\ \\ \implies { \begin{bmatrix} {1} & {1} \\ {-1/2} & {1} \end{bmatrix} } \begin{bmatrix} c_1 \\ c_2 \end{bmatrix} &= \begin{bmatrix} a \\ b \end{bmatrix} \\ \implies \begin{bmatrix} c_1 \\ c_2 \end{bmatrix} &= {1\over 1 + (1/2)} { \begin{bmatrix} {1} & {-1} \\ {1/2} & {1} \end{bmatrix} } \begin{bmatrix} a \\ b \end{bmatrix} \\ &= \qty{1\over 3} { \begin{bmatrix} {2} & {-2} \\ {1} & {2} \end{bmatrix} } \begin{bmatrix} a \\ b \end{bmatrix} \\ &= \qty{1\over 3} \begin{bmatrix} 2a-2b \\ a+b \end{bmatrix} .\end{align*}
So the general solution is \begin{align*} x_n = {2\over 3}(a-b) \qty{-1\over 2}^n + {1\over 3}(a+b)\overset{n\to \infty}\longrightarrow \qty{1\over 3}(a+b) .\end{align*}
Uniform continuity
Suppose \(f:{\mathbb{R}}\to{\mathbb{R}}\) is continuous and \(\lim_{x\to \pm \infty} f(x) = 0\). Prove that \(f\) is uniformly continuous.
Fix \({\varepsilon}>0\), we need to find a \(\delta = \delta({\varepsilon})\) such that \begin{align*} {\left\lvert {x-y} \right\rvert}<\delta \implies {\left\lvert {f(x) - f(y)} \right\rvert} < {\varepsilon}&& \forall x, y\in {\mathbb{R}} .\end{align*} Use that \(\lim_x\to \pm \infty f(x) = 0\) to choose \(M\gg 0\) such that \begin{align*} {\left\lvert {x} \right\rvert} \geq M \implies {\left\lvert {f(x)} \right\rvert} \leq {\varepsilon}/2 ,\end{align*} then \begin{align*} {\left\lvert {x} \right\rvert}, {\left\lvert {y} \right\rvert} \geq M \implies {\left\lvert {f(x) - f(y)} \right\rvert} \leq {\left\lvert {f(x)} \right\rvert} + {\left\lvert {f(y)} \right\rvert} \leq {\varepsilon} .\end{align*} So in this region choose (say) \(\delta_1 < {\varepsilon}\) to ensure that \(B_\delta(x), B_\delta(y) \subseteq [-M, M]^c\). On \([-M, M]\), note that this region is compact and \(f\) continuous on a compact set implies uniformly continuous. So use this to choose \(\delta_2 = \delta_2({\varepsilon})\) in this region to ensure \({\left\lvert {f(x) - f(y)} \right\rvert} < {\varepsilon}\).
This handles the cases \(x, y \in (M, M)^c\), or \(x,y\in [M, M]\), so it only remains to handle \(x\in [M, M]\) and \(y\in (M, M)^c\) (wlog, relabeling \(x,y\) if necessary). In this case, use the triangle inequality: \begin{align*} {\left\lvert {f(x) - f(y)} \right\rvert} &= {\left\lvert {f(x) - f(M) + f(M) -f(y)} \right\rvert} \\ &\leq {\left\lvert {f(x) - f(M)} \right\rvert} + {\left\lvert {f(M) -f(y)} \right\rvert} \\ &\leq {\varepsilon}+ {\left\lvert {f(M)} \right\rvert} + {\left\lvert {f(y)} \right\rvert} \\ &\leq {\varepsilon}+ {\varepsilon}+ {\varepsilon} ,\end{align*} where we’ve used that \(M, y\in (M, M)^c\) to apply the first bound and \(M, x\in [M, M]\) to apply the second.
Negating uniform continuity
Tie, Fall 2009
Show that \(f(z) = z^2\) is uniformly continuous in any open disk \(|z| < R\), where \(R>0\) is fixed, but it is not uniformly continuous on \(\mathbb C\).
A direct computation: fix \({\varepsilon}>0\) and suppose \({\left\lvert {z-w} \right\rvert} < R\). Then \begin{align*} {\left\lvert {z^2-w^2} \right\rvert} &= {\left\lvert {z-w} \right\rvert}{\left\lvert {z+w} \right\rvert} \\ &\leq \delta \qty{{\left\lvert {z} \right\rvert} + {\left\lvert {w} \right\rvert}} \\ &\leq \delta \cdot 2R ,\end{align*} so choose \(\delta < { {\varepsilon}\over 2R}\) to get uniform continuity on \({\mathbb{D}}_{R/2}(0)\).
To see \(f\) can’t be uniformly continuous on \({\mathbb{C}}\), take \({\varepsilon}\coloneqq c\) any constant and suppose the appropriate \(\delta\) exists. We’ll look for a bad pair of \(z, w\), so take \(w = z + {1\over 2}\delta\). This would imply \begin{align*} {\left\lvert {z^2 - w^2} \right\rvert} &= {\left\lvert {z^2 - (z+\delta)^2} \right\rvert} \\ &= {\left\lvert {-2z\delta - \delta^2} \right\rvert} \\ &= {\left\lvert {2z\delta + \delta^2} \right\rvert} \\ &= \delta {\left\lvert {2z + \delta} \right\rvert} \\ &\overset{{\left\lvert {z} \right\rvert}\to\infty}\longrightarrow\infty ,\end{align*} using the \(\delta = \delta({\varepsilon})\) can’t depend on \(z\) or \(w\), and is thus constant in this expression. This contradicts that \({\left\lvert {z^2-w^2} \right\rvert} < {\varepsilon}= c < \infty\).
Non-continuously differentiable
Give an example of a function \(f:{\mathbb{R}}\to {\mathbb{R}}\) that is everywhere differentiable but \(f'\) is not continuous at 0.
The standard example: \begin{align*} f(x) \coloneqq \begin{cases} x^2\sin\qty{1\over x} & x\neq 0 \\ 0 & x=0. \end{cases} .\end{align*}
Away from zero, this is clearly differentiable since we can just compute the derivative by the chain rule. It turns out that \begin{align*} f'(x) = \begin{cases} 2x\sin\qty{1\over x} + x^2 \cos\qty{1\over x}\qty{-1\over x^2} = 2x\sin\qty{1\over x} - \cos\qty{1\over x} & x\neq 0 \\ 0 & x=0. \end{cases} .\end{align*} Here we check differentiability and compute the derivative at \(x=0\) directly: \begin{align*} {f(x) - f(0) \over x-0} = {x^2\sin\qty{1\over x} - 0 \over x-0} = x\sin\qty{1\over x} \overset{x\to 0}\longrightarrow 0 ,\end{align*} using that \(-x \leq {\left\lvert {x\sin \qty{1\over x}} \right\rvert}\leq x\).
But now notice that the \(\cos\qty{1\over x}\) term in \(f'\) isn’t enveloped by an \(x^c\) term, so \(\lim_{x\to 0} f'(x)\) does not exist for oscillatory reasons:
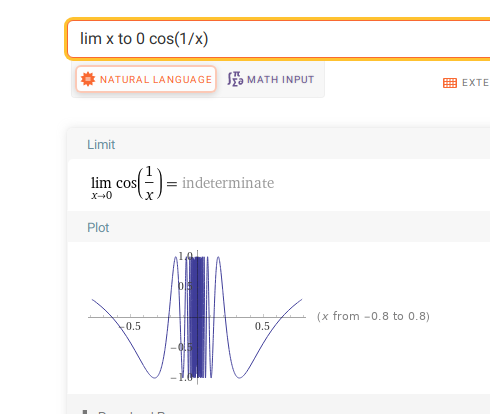
In particular, \(\lim_{x\to 0}f'(x) \neq f'(0) = 0\).
Uniformly convergent + uniformly continuous
Suppose \(\left\{{g_n}\right\}\) is a uniformly convergent sequence of functions from \({\mathbb{R}}\) to \({\mathbb{R}}\) and \(f:{\mathbb{R}}\to {\mathbb{R}}\) is uniformly continuous. Prove that the sequence \(\left\{{f\circ g_n}\right\}\) is uniformly convergent.
Uniformly convergent means that \({\left\lVert {g_i - g_j} \right\rVert}_{\infty} \to 0\), so \(\sup_{x\in X}{\left\lvert {g_i(x)-g_j(x)} \right\rvert} \overset{i, j\to\infty}\longrightarrow 0\). We want to show that given \({\varepsilon}\) we can find \(N_0\) such that \(i, j > N_0\) yields \begin{align*} \sup_{x\in X}{\left\lvert { f\circ g_i(x) - f\circ g_j(x) } \right\rvert} < {\varepsilon} .\end{align*}
Fix \({\varepsilon}> 0\), then choose \(\delta_1 = \delta_1({\varepsilon})\) by uniform continuity of \(f\) to guarantee \begin{align*} {\left\lvert {y_1 - y_2} \right\rvert} \leq \delta_1 \implies {\left\lvert {f(y_1) - f(y_2) } \right\rvert} < {\varepsilon}\, \forall y_1, y_2\in X .\end{align*} Now by uniform convergence of \(\left\{{g_n}\right\}\), choose \(N_0 = N_0(\delta_1)\) such that \begin{align*} i, j \geq N_0 \implies {\left\lvert { g_i(x) - g_j(x) } \right\rvert} < \delta_1 \, \forall x\in X .\end{align*}
Now writing \(y_1 \coloneqq g_i(x), y_2 \coloneqq g_j(x)\), choose \(i, j > N_0\) yields \begin{align*} {\left\lvert {y_1 - y_2} \right\rvert} \coloneqq{\left\lvert {g_i(x) - g_j(x) } \right\rvert} < \delta_1 \\ \implies {\left\lvert {f(y_1) - f(y_2)} \right\rvert} \coloneqq{\left\lvert {f(g_i(x)) - f(g_j(x))} \right\rvert} < {\varepsilon} ,\end{align*} and taking the supremum over \(x\in X\) preserves the inequality since \(\delta_1\) and consequently \(N_0\) only depend on \({\varepsilon}\).
Uniform differentiability
Let \(f\) be differentiable on \([a, b]\). Say that \(f\) is uniformly differentiable iff
\begin{align*} \forall \varepsilon > 0,\, \exists \delta > 0 \text{ such that } \quad {\left\lvert {x-y} \right\rvert} < \delta \implies {\left\lvert { {f(x) - f(y) \over x-y} - f'(y)} \right\rvert} < {\varepsilon} .\end{align*}
Prove that \(f\) is uniformly differentiable on \([a, b] \iff f'\) is continuous on \([a, b]\).
\(\implies\): Fix \({\varepsilon}>0\) and choose \(\delta = \delta({\varepsilon})\) to get a bound corresponding to \({\varepsilon}/2\), then for all \(x,y\) with \({\left\lvert {x-y} \right\rvert} < \delta\) on \([a, b]\), we have \begin{align*} {\left\lvert {f'(x) - f'(y) } \right\rvert} \leq {\left\lvert {f'(x) - {f(x) - f(y) \over x- y} } \right\rvert} + {\left\lvert { {f(x) - f(y) \over x-y} - f'(y)} \right\rvert} < {\varepsilon} .\end{align*} This uses uniformity to bound by \({\varepsilon}/2\) the terms involving \(f'(x)\) and \(f'(y)\) respectively. So \(f'\) is in fact uniformly continuous on \([a, b]\).
\(\impliedby\): Let \({\varepsilon}> 0\) and \(x,y\in [a, b]\) be arbitrary. Then by the MVT, we can a \(\xi\in [x, y]\) with \(f'(\xi)(x-y) = f(x) - f(y)\). Then use continuity of \(f'\) to choose \(\delta = \delta({\varepsilon}, x, y)\) so that \({\left\lvert {x-y} \right\rvert} < \delta \implies {\left\lvert {f(x) - f(y)} \right\rvert} < {\varepsilon}\), and note that \({\left\lvert {x-\xi} \right\rvert} \leq {\left\lvert {x-y} \right\rvert} < \delta\), so \begin{align*} {\left\lvert { {f(x) - f(y) \over x-y } - f'(y) } \right\rvert} = {\left\lvert { f'(\xi) - f'(y)} \right\rvert} < {\varepsilon} .\end{align*}
Inf distance
Suppose \(A, B \subseteq {\mathbb{R}}^n\) are disjoint and compact. Prove that there exist \(a\in A, b\in B\) such that \begin{align*} {\left\lVert {a - b} \right\rVert} = \inf\left\{{{\left\lVert {x-y} \right\rVert} {~\mathrel{\Big\vert}~}x\in A,\, y\in B}\right\} .\end{align*}
Define a function \begin{align*} d: A \times B &\to {\mathbb{R}}\\ (x, y) &\mapsto {\left\lVert {x- y} \right\rVert} .\end{align*} Then \(d\) is a continuous function on a compact topological space (where the product is compact by Tychonoff), and the extreme value theorem applies: \(d\) attains its min/max for some pair \((a, b)\) in its domain.
Note that disjointness just guarantees that \({\left\lVert {a-b} \right\rVert}>0\), since \({\left\lVert {a-b} \right\rVert} = 0 \implies a=b\) and \(A \cap B = \emptyset\).
Connectedness
Suppose \(A, B\subseteq {\mathbb{R}}^n\) are connected and not disjoint. Prove that \(A\cup B\) is also connected.
Use that \(X\) is connected iff \(\mathop{\mathrm{Hom}}_{{\mathsf{Top}}}(X, S^0) = \left\{{c_{-1}, c_1}\right\}\), i.e. every continuous map from \(X\to \left\{{-1, 1}\right\}\) is a constant map \(x \xrightarrow{c_{-1}} -1\) or \(x \xrightarrow{c_1} 1\). Let \(f: A\cup B \to S^0\) be arbitrary, and let \(f_1 \coloneqq{ \left.{{f}} \right|_{{A}} }\) and \(f_2 \coloneqq{ \left.{{f}} \right|_{{B}} }\). By connectedness of \(A\), \(f_1\) is a constant map, as is \(f_2\). On the intersection, for \(x\in A \cap B \neq \emptyset\), we have \(f_1(x) = f_2(x)\) since \(x\in A\) and \(x\in B\). So \(f_1\) and \(f_2\) are constant functions that must map to the same constant, so \(f\) is constant and this \(A\cup B\) is connected.
Pointwise and uniform convergence
Suppose \(\left\{{f_n}\right\}_{n\in {\mathbb{N}}}\) is a sequence of continuous functions \(f_n: [0, 1]\to {\mathbb{R}}\) such that \begin{align*} f_n(x) \geq f_{n+1}(x) \geq 0 \quad \forall n\in {\mathbb{N}},\, \forall x\in [0, 1] .\end{align*} Prove that if \(\left\{{f_n}\right\}\) converges pointwise to \(0\) on \([0, 1]\) then it converges to \(0\) uniformly on \([0, 1]\).
Let \({\varepsilon}>0\), we want to show that there exists an \(N_0\) such that \(n\geq N_0\) implies \({\left\lVert {f_n} \right\rVert}_\infty<{\varepsilon}\). Fix \(x\), by pointwise convergence pick \(M_x = M_x(x, {\varepsilon})\) so that \(n\geq M \implies {\left\lvert {f_n(x)} \right\rvert} < {\varepsilon}\). By continuity, this bound holds in some neighborhood \(U_x \ni x\). Produce a cover \(\left\{{U_x}\right\}_{x\in [0, 1]}\rightrightarrows[0, 1]\); by compactness produce a finite subcover \(\left\{{U_1, \cdots, U_m}\right\} \rightrightarrows[0, 1]\). Each \(U_i\) corresponds to some \(x_i\) and some \(M_{x_i}\), so choose \(N_0 > \max_{i\leq m} \left\{{M_{x_i}}\right\}\). Then \(n\geq N_0 \implies N\geq M_{x_i}\) for each \(i\), so \({\left\lvert {f_n(x)} \right\rvert} < {\varepsilon}\) for each \(x\in [0, 1]\) since \(x\in U_i\) for some \(i\). So \(\sup_{x\in X} {\left\lvert {f_n(x)} \right\rvert} = {\left\lVert {f_n} \right\rVert}_{\infty } < {\varepsilon}\).
Show that if \(E\subset [0, 1]\) is uncountable, then there is some \(t\in {\mathbb{R}}\) such that \(E\cap(-\infty ,t)\) and \(E\cap(t, \infty)\) are also uncountable.
See 3.2.12 of Understanding analysis 2ed. of Abbott. Show something stronger, that the following set is nonempty and open: \begin{align*} S \coloneqq\left\{{t\in {\mathbb{R}}{~\mathrel{\Big\vert}~}E \cap(-\infty, t), E \cap(t, \infty) \text{ are uncountable}}\right\} \subseteq {\mathbb{R}} .\end{align*} Write \begin{align*} S_- &\coloneqq\left\{{ t\in {\mathbb{R}}{~\mathrel{\Big\vert}~}E \cap(- \infty, t) \text{ is countable}}\right\} \\ S_+ &\coloneqq\left\{{ s\in {\mathbb{R}}{~\mathrel{\Big\vert}~}E \cap(s, \infty) \text{ is countable}}\right\} .\end{align*}
Note that \(S_- \neq {\mathbb{R}}\) since then we could write \(E = \displaystyle\bigcup_{n\in {\mathbb{Z}}} E \cap(- \infty, n)\) as a countable union of countable sets.
Claim: \(S = (\sup S_-,, \inf S_+)\).
???
Suppose \(f, g: [0, 1] \to {\mathbb{R}}\) where \(f\) is Riemann integrable and for \(x, y\in [0, 1]\), \begin{align*} {\left\lvert {g(x) - g(y)} \right\rvert} \leq {\left\lvert {f(x) - f(y)} \right\rvert} .\end{align*}
Prove that \(g\) is Riemann integrable.
Write \(U(f), L(f)\) for the upper and lower sums of \(f\), so for \(\Pi\) the collection of all partitions of \([0, 1]\), \begin{align*} U(f) \coloneqq\inf_{P\in \Pi} U(f, P) && U(f, P) \coloneqq\sum_{k=1}^n \sup_{x\in I_k}f(x) \cdot \mu(I_k) \\ L(f) \coloneqq\sup_{P\in \Pi} L(f, P) && L(f, P) \coloneqq\sum_{k=1}^n \inf_{x\in I_k} f(x) \cdot \mu(I_k) .\end{align*}
Note that integrability of \(f\) is equivalent to \begin{align*} \forall {\varepsilon}\exists P \text{ such that } U(f, P) - L(f, P) < {\varepsilon}\\ \iff \sum_{k=1}^n \qty{ \sup_{x\in I_k} f(x) - \inf_{x\in I_k} f(x)} \mu(I_k) < {\varepsilon} .\end{align*}
Exercises
Show that \(f(x) = x^n\) is uniformly continuous on any interval \([-M, M]\).
\
\begin{align*} {\left\lvert {x^n - y^n} \right\rvert} = {\left\lvert {y-x} \right\rvert}{\left\lvert {\sum_{1\leq k \leq n} x^k y^{n-k}} \right\rvert} \leq n M^{n-1}{\left\lvert {y-x} \right\rvert} \overset{y\to x}\longrightarrow 0 .\end{align*}
Show \(f(x) = x^{-n}\) for \(n\in {\mathbb{Z}}_{\geq 0}\) is uniformly continuous on \([0, \infty)\).
\
\begin{align*} x^{1\over n} - y^{1\over n} \leq (x-y)^{1\over n} \overset{x\to y}\longrightarrow 0 ,\end{align*} using \((a+b)^m \geq a^m + b^m\)
Show that \(f'\) bounded implies \(f\) is uniformly continuous.
\
Apply the MVT: \begin{align*} {\left\lvert {f(x) - f(y)} \right\rvert} = {\left\lvert {f(\xi)} \right\rvert} {\left\lvert {x-y} \right\rvert} \overset{y\to x}\longrightarrow 0 .\end{align*}
Show that the Dirichlet function \(f(x) = \chi_{I \cap{\mathbb{Q}}}\) is not Riemann integrable and is everywhere discontinuous.
\
Check \(\sup f = 1\) and \(\inf f = 0\) on every sub-interval, so \(L(f, P) = 0\) and \(U(f, P) = 1\) for every partition \(P\) of \([0, 1]\).
Discontinuity: #todo
Continuity
1
Is the following function continuous, differentiable, continuously differentiable? \begin{align*} f: {\mathbb{R}}^2 &\to {\mathbb{R}}\\ f(x, y) &= \begin{cases} {xy \over \sqrt{x^2 + y^2}} & (x, y) \neq (0, 0) \\ 0 & \text{else}. \end{cases} \end{align*}
?
Show that \(f(z) = z^2\) is uniformly continuous in any open disk \(|z| < R\), where \(R>0\) is fixed, but it is not uniformly continuous on \(\mathbb C\).
6
Let \(F:{\mathbb{R}}^2\to {\mathbb{R}}\) be continuously differentiable with \(F(0, 0) = 0\) and \({\left\lVert {\nabla F(0, 0)} \right\rVert} < 1\).
Prove that there is some real number \(r> 0\) such that \({\left\lvert {F(x, y)} \right\rvert} < r\) whenever \({\left\lVert {(x, y)} \right\rVert} < r\).
2 Multivariable derivatives
-
Complete this definition: “\(f: {\mathbb{R}}^n\to {\mathbb{R}}^m\) is real-differentiable a point \(p\in {\mathbb{R}}^n\) iff there exists a linear transformation…”
-
Give an example of a function \(f:{\mathbb{R}}^2\to {\mathbb{R}}\) whose first-order partial derivatives exist everywhere but \(f\) is not differentiable at \((0, 0)\).
- Give an example of a function \(f: {\mathbb{R}}^2 \to {\mathbb{R}}\) which is real-differentiable everywhere but nowhere complex-differentiable.
Implicit/Inverse Function Theorems
3
Let \(f:{\mathbb{R}}^2\to {\mathbb{R}}\).
-
Define in terms of linear transformations what it means for \(f\) to be differentiable at a point \((a, b) \in {\mathbb{R}}^2\).
-
State a version of the inverse function theorem in this setting.
- Identify \({\mathbb{R}}^2\) with \({\mathbb{C}}\) and give a necessary and sufficient condition for a real-differentiable function at \((a, b)\) to be complex differentiable at the point \(a+ib\).
5
Let \(P = (1, 3) \in {\mathbb{R}}^2\) and define \begin{align*} f(s, t) \coloneqq ps^3 -6st + t^2 .\end{align*}
-
State the conclusion of the implicit function theorem concerning \(f(s, t) = 0\) when \(f\) is considered a function \({\mathbb{R}}^2\to{\mathbb{R}}\).
-
State the above conclusion when \(f\) is considered a function \({\mathbb{C}}^2\to {\mathbb{C}}\).
- Use the implicit function theorem for a function \({\mathbb{R}}\times{\mathbb{R}}^2 \to {\mathbb{R}}^2\) to prove (b).
There are various approaches: using the definition of the complex derivative, the Cauchy-Riemann equations, considering total derivatives, etc.
7
State the most general version of the implicit function theorem for real functions and outline how it can be proved using the inverse function theorem.
Complex Differentiability
4
Let \(f = u+iv\) be complex-differentiable with continuous partial derivatives at a point \(z = re^{i\theta}\) with \(r\neq 0\). Show that \begin{align*} {\frac{\partial u}{\partial r}\,} = {1\over r}{\frac{\partial v}{\partial \theta}\,} \qquad {\frac{\partial v}{\partial r}\,} = -{1\over r}{\frac{\partial u}{\partial \theta}\,} .\end{align*}
Tie’s Extra Questions: Fall 2016
Let \(u(x,y)\) be harmonic and have continuous partial derivatives of order three in an open disc of radius \(R>0\).
-
Let two points \((a,b), (x,y)\) in this disk be given. Show that the following integral is independent of the path in this disk joining these points: \begin{align*} v(x,y) = \int_{a,b}^{x,y} ( -\frac{\partial u}{\partial y}dx + \frac{\partial u}{\partial x}dy) .\end{align*}
-
In parts:
- Prove that \(u(x,y)+i v(x,y)\) is an analytic function in this disc.
- Prove that \(v(x,y)\) is harmonic in this disc.
Tie’s Questions, Spring 2014: Polar Cauchy-Riemann
Let \(f=u+iv\) be differentiable (i.e. \(f'(z)\) exists) with continuous partial derivatives at a point \(z=re^{i\theta}\), \(r\not= 0\). Show that \begin{align*} \frac{\partial u}{\partial r}=\frac{1}{r}\frac{\partial v}{\partial \theta},\quad \frac{\partial v}{\partial r}=-\frac{1}{r}\frac{\partial u}{\partial \theta} .\end{align*}
?
-
Show that the function \(u=u(x,y)\) given by \begin{align*} u(x,y)=\frac{e^{ny}-e^{-ny}}{2n^2}\sin nx\quad \text{for}\ n\in {\mathbf N} \end{align*} is the solution on \(D=\{(x,y)\ | x^2+y^2<1\}\) of the Cauchy problem for the Laplace equation \begin{align*}\frac{\partial ^2u}{\partial x^2}+\frac{\partial ^2u}{\partial y^2}=0,\quad u(x,0)=0,\quad \frac{\partial u}{\partial y}(x,0)=\frac{\sin nx}{n}.\end{align*}
-
Show that there exist points \((x,y)\in D\) such that \(\displaystyle{\limsup_{n\to\infty} |u(x,y)|=\infty}\).
Montel
Convergence of holomorphic functions on line segments
Suppose \(\left\{{f_n}\right\}_{n\in {\mathbb{N}}}\) is a sequence of entire functions where
- \(f_n \to g\) pointwise for some \(g:{\mathbb{C}}\to{\mathbb{C}}\).
- On every line segment in \({\mathbb{C}}\), \(f_n \to g\) uniformly.
Show that
- \(g\) is entire, and
- \(f_n\to g\) uniformly on every compact subset of \({\mathbb{C}}\).
Note that \(g\) is entire by Morera’s theorem, since \(0 = \int_T f_n \to \int_T g\) by uniform convergence and the \(f_n\) are holomorphic. By Cauchy’s theorem, up to a constant we have \begin{align*} f_n(z) = \oint_T {f_n(\xi) \over \xi - z}\,d\xi g(z) = \oint_T {g(\xi) \over \xi - z}\,d\xi ,\end{align*} Thus fixing \(K\) and \({\varepsilon}\), for any \(T \subseteq K\) containing \(z\), ` \begin{align*} {\left\lvert {f_n(z) - g(z)} \right\rvert} &= {\left\lvert { \oint_T {f_n(\xi) \over \xi - z},d\xi
- \oint_T {g(\xi) \over \xi - z},d\xi } \right\rvert} \ &\leq \oint_T {{\left\lvert {f_n(\xi) - g(\xi)} \right\rvert} \over \xi - z },d\xi\ &\leq \oint_T { \sup_{\xi\in T}{\left\lvert {f_n(\xi) - g(\xi)} \right\rvert} \over \xi - z },d\xi\ &\leq \oint_T { {\varepsilon}\over \xi - z },d\xi\ &= {\varepsilon}C \to 0 ,\end{align*} `{=html} where \(n = n({\varepsilon}, T)\) can be chosen to produce this \({\varepsilon}\) using that \(f_n\to g\) uniformly on \(T\). Taking a sup over the \(z\) enclosed by \(T\) on the LHS yields a bound on the open region enclosed by \(T\). Taking a union of all such \(T\) in \(K\) yields an open cover of \(K\), which by compactness has a finite subcover. This yields a finite collection \(\left\{{n = n({\varepsilon}, T_k)}\right\}_{k\leq N}\), and taking the maximum such \(n\) yields a uniform bound for all of \(K\).
Tie’s Extra Questions: Spring 2015
Assume \(f_n \in H(\Omega)\) is a sequence of holomorphic functions on the region \(\Omega\) that are uniformly bounded on compact subsets and \(f \in H(\Omega)\) is such that the set \(\displaystyle \{z \in \Omega: \lim_{n \rightarrow \infty} f_n(z) = f(z) \}\) has a limit point in \(\Omega\). Show that \(f_n\) converges to \(f\) uniformly on compact subsets of \(\Omega\).
Spring 2019.7
^d94130
Let \(\Omega \subset {\mathbb{C}}\) be a connected open subset. Let \(\left\{f_{n}: \Omega \rightarrow {\mathbb{C}}\right\}_{n=1}^{\infty}\) be a sequence of holomorphic functions uniformly bounded on compact subsets of \(\Omega\). Let \(f: \Omega \rightarrow {\mathbb{C}}\) be a holomorphic function such that the set \begin{align*} \left\{z \in \Omega \mathrel{\Big|}\lim _{n \rightarrow \infty} f_{n}(z)=f(z)\right\} \end{align*} has a limit point in \(\Omega\). Show that \(f_{n}\) converges to \(f\) uniformly on compact subsets of \(\Omega\).
Write \(g(z) \coloneqq\lim_{n\to\infty}f_n(z)\) for the pointwise limit, then \(g(z) = f(z)\) on a set with a limit point. By the identity principle, \(g\equiv f\) on \(\Omega\), making \(f\) the pointwise limit of the \(f_n\).
By Montel, locally uniformly bounded implies normal and locally equicontinuous. So \(\left\{{f_n}\right\}\) is normal, and thus has a locally uniformly convergent subsequence \(\left\{{f_{n_k}}\right\}\). Since singletons \(\left\{{z}\right\}\) are compact, \(f_{n_k}(z) \to g(z)\) pointwise, and by uniqueness of limits, \(\lim_{k\to\infty } f_{n_k} = g = f\) on any compact \(K \subseteq \Omega\).
It remains to show that the original sequence \(\left\{{f_n}\right\}\) converges locally uniformly to \(f\), not just the subsequence. Suppose not, then there exists a compact \(K \subseteq \Omega\) and \({\varepsilon}>0\) so that \({\left\lVert {f_n - f} \right\rVert}_{K, \infty} > {\varepsilon}\) for infinitely many \(n\). This produces a subsequence \(\left\{{f_{n_j}}\right\}\) with \({\left\lVert {f_{n_j} - f} \right\rVert} > {\varepsilon}\) for all \(j\). However, since \({\mathcal{F}}\) was normal, every subsequence has a locally uniformly convergent subsequence, so this has a further subsequence \(f_{n_{j'}}\) uniformly converging to \(f\), a contradiction.
Function Convergence
Fall 2021.4
^b0c999
Prove that the sequence \(\left(1+\frac{z}{n}\right)^{n}\) converges uniformly to \(e^{z}\) on compact subsets of \(\mathbb{C}\).
Hint: \(e^{n \log w_{n}}=w_{n}^{n}\) and \(e^{z}\) is uniform continuous on compact subsets of \(\mathbb{C}\).
Let \(K\) be compact, where \(z\in K\implies {\left\lvert {z} \right\rvert} \leq R\) for some constant \(R\). For the remainder of the problem, we only work in \(K\).
\(f_n(z) \coloneqq n\log(1 + {z\over n}) \to z\) uniformly.
\(f_n\) are uniformly bounded on \(K\).
\(e^z\) is uniformly continuous on \(K\).
If \(g_n\to g\) uniformly and \(F\) is uniformly continuous, then \(F \circ g_n \to F\circ g\) uniformly.
Why these claims imply the result:
If \(f_n(z)\to z\) uniformly, both are uniformly bounded, and \(e^z\) is uniformly continuous, then \(e^{f(z)}\to e^z\) uniformly.
We’ll first show that for \(w\) in a neighborhood of zero avoiding 1, there exists a constant \(C\) such that \begin{align*} {\left\lvert { 1 - {\log(1+w) \over w} } \right\rvert} \leq C{\left\lvert {w} \right\rvert} .\end{align*} This follows from estimating the series expansion about \(w=0\): \begin{align*} {\left\lvert { 1 - {\log(1+w) \over w} } \right\rvert} &= {\left\lvert {w^{-1}\sum_{k\geq 1} { (-w)^k \over k} } \right\rvert} \\ &= {\left\lvert {\sum_{k\geq 2} {(-w)^{k-1} \over k} } \right\rvert} \\ &\leq {\sum_{k\geq 2} {{\left\lvert {w} \right\rvert}^{k-1} \over k} } \\ &= {\sum_{k\geq 1} {{\left\lvert {w} \right\rvert}^{k} \over k+1} } \\ &\leq {\sum_{k\geq 1} {{\left\lvert {w} \right\rvert}^{k} \over 2} } \\ &= {1\over 2}\qty{{1\over 1 - {\left\lvert {w} \right\rvert}} - 1 } \\ &= {1\over 2}{\left\lvert {2} \right\rvert} \qty{1\over 1 - {\left\lvert {w} \right\rvert}} \\ &\leq C {\left\lvert {w} \right\rvert} ,\end{align*} using that \({1\over 1-x}\) is bounded in compact sets avoiding \(x=1\).
We can now apply the \(M{\hbox{-}}\)test: \begin{align*} {\left\lvert {n\log\qty{ 1 + {z\over n} } - z } \right\rvert} &= {\left\lvert {z} \right\rvert}\cdot {\left\lvert { {{ \log\qty{1 + {z\over n}} \over {z\over n}} - 1} } \right\rvert} \\ &\leq {\left\lvert {z} \right\rvert} \cdot C{\left\lvert {z\over n} \right\rvert} \\ &\leq M\cdot C\qty{M\over n} \\ &= {CM^2 \over n}\\ &\overset{n\to\infty}\longrightarrow 0 .\end{align*}
Spring 2021.6, Spring 2015, Extras
^c94b57
Let \(\left\{{f_n}\right\}_{n=1}^\infty\) is a sequence of holomorphic functions on \({\mathbb{D}}\) and \(f\) is also holomorphic on \({\mathbb{D}}\). Show that the following are equivalent:
- \(f_n\to f\) uniformly on compact subsets of \({\mathbb{D}}\).
- For \(0 < r < 1\), \begin{align*} \int_{{\left\lvert {z} \right\rvert} = r} {\left\lvert {f_n(z) - f(z)} \right\rvert} {\left\lvert {dz} \right\rvert} \overset{n\to\infty}\longrightarrow 0 .\end{align*}
Note: \({\left\lvert {\,dz} \right\rvert} = {\left\lvert {\gamma'(t)} \right\rvert}\,dt\) for \(\gamma\) a parameterization of the curve.
\(\implies\):
- Fix \(r \in (0, 1)\) and let \(\gamma = \left\{{{\left\lvert {z} \right\rvert} = r}\right\}\). This is compact, so \(f_n\to f\) uniformly on \(\gamma\): \begin{align*} \int_\gamma {\left\lvert {f_n(z) - f(z) } \right\rvert} \,dz &\leq\int_\gamma \sup_{w\in \gamma } {\left\lvert {f_n(w) - f(w) } \right\rvert} \,dz\\ &\leq\int_\gamma {\left\lVert {f_n(w) - f(w) } \right\rVert}_{\infty} \,dz\\ &= {\left\lVert {f_n(w) - f(w) } \right\rVert}_{\infty} \int_\gamma \,dz\\ &= {\left\lVert {f_n(w) - f(w) } \right\rVert}_{\infty} \mathop{\mathrm{length}}(\gamma) \\ &\overset{n\to\infty}\longrightarrow 0 .\end{align*}
\(\impliedby\):
-
Let \(K\) be compact, then choose \(\gamma\) enclosing but not intersecting \(K\).
-
Since \(\gamma, K\) are disjoint compact sets, define \(M \coloneqq\inf \left\{{{\left\lvert {z-\xi} \right\rvert} {~\mathrel{\Big\vert}~}z\in K, \xi\in \gamma}\right\}\), the \(0<M<\infty\).
-
Apply Cauchy’s formula to the function \(F_n(z) \coloneqq f_n(z) - f(z)\), where we want to show \({\left\lvert {F_n(z)} \right\rvert} < {\varepsilon}\): \begin{align*} F_n(z) &= {1\over 2\pi i} \int_\gamma { F_n(\xi) \over z-\xi} \,d\xi\\ \implies {\left\lvert {f_n(z) - f(z) } \right\rvert} &\leq {1\over 2\pi }\int_\gamma {\left\lvert {f_n(\xi) - f(\xi) \over z-\xi} \right\rvert} \,d\xi\\ &\leq {1\over 2\pi} \int_\gamma {{\left\lvert { f_n(\xi) - f(\xi) } \right\rvert} \over M} \,d\xi\\ &\leq {1\over 2\pi M} \int_\gamma {{\left\lvert { f_n(\xi) - f(\xi) } \right\rvert} } {\left\lvert {\,d\xi} \right\rvert} \\ ,\end{align*} where by hypothesis we can bound this integral by an \({\varepsilon}\). So given \({\varepsilon}\), choose \(n\) large enough to bound the integral as above by some \({\varepsilon}\) depending only on \(n\) and not on \(z\). Taking \(\sup\) of both sides yields \({\left\lVert {f_n - f} \right\rVert}_{\infty, K} \leq {{\varepsilon}\over 2\pi M}\), so \(f_n\to f\) uniformly on \(K\).
Spring 2020 HW 2, SS 2.6.10
Can every continuous function on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) be uniformly approximated by polynomials in the variable \(z\)?
Hint: compare to Weierstrass for the real interval.
No: polynomials are holomorphic and the uniform limit of holomorphic functions is holomorphic. However, \(f(z) \coloneqq\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu\) is continuous on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) but not holomorphic, so can not be uniformly approximated by any sequence of polynomials.
Spring 2020 HW 2.5
Assume \(f\) is continuous in the region \(\left\{{x+iy {~\mathrel{\Big\vert}~}x\geq x_0, ~ 0\leq y \leq b}\right\}\), and the following limit exists independent of \(y\): \begin{align*} \lim_{x\to +\infty}f(x+iy) = A .\end{align*}
Show that if \(\gamma_x \coloneqq\left\{{z = x+it {~\mathrel{\Big\vert}~}0 \leq t \leq b}\right\}\), then \begin{align*} \lim_{x\to +\infty} \int_{\gamma_x} f(z) \,dz = iAb .\end{align*}
The key insight: \begin{align*} \int_\gamma A \,dz &= \int_0^b A \cdot i \,dt&& z=x+it,\, \,dz= i\,dt\\ &=iA \int_0^b \,dt\\ &= iAb .\end{align*}
So now estimate the difference: \begin{align*} {\left\lvert { \int_{\gamma} f(z) \,dz- iAb } \right\rvert} &= {\left\lvert { \int_\gamma f(z) \,dz- \int_\gamma A \,dz} \right\rvert} \\ &= {\left\lvert { \int_\gamma \qty{ f(z) - A } \,dz} \right\rvert} \\ &\leq\int_\gamma {\left\lvert { f(z) - A } \right\rvert} \,dz\\ &\leq \sup_{z = x+iy\in \gamma} {\left\lvert {f(x+iy) - A} \right\rvert} \cdot \mathop{\mathrm{length}}(\gamma_x) \\ &\overset{x\to \infty}\longrightarrow 0 ,\end{align*} using that \(\mathop{\mathrm{length}}(\gamma_x) = b\) is constant.
Limiting curve variant
Let \(0\leq \alpha \leq 2\pi\) be a fixed angle. Suppose \(f\) is continuous on the region \(\Omega = \left\{{{\left\lvert {z} \right\rvert} \geq R, \operatorname{Arg}(z) \in [0, \alpha]}\right\}\) and \(\lim_{z\to \infty} zf(z) = A\). Show that \begin{align*} \lim_{z\to \infty} \int_{\gamma_R} f(z) \,dz= iA\alpha ,\end{align*} where \(\gamma_R \coloneqq\left\{{ {\left\lvert {z} \right\rvert} = R, \operatorname{Arg}(z) \in [0, \alpha]}\right\}\) is an arc.
Key observation: \begin{align*} iA\alpha = \int_\gamma {A\over z}\,dz .\end{align*} Why this is true: \begin{align*} \int_\gamma {A\over z}\,dz= \int_0^\alpha {1\over Re^{it}} iRe^{it}dt = \int_0^\alpha iA \,dt= iA\alpha .\end{align*}
Now estimate the difference:
\begin{align*} {\left\lvert { \int_\gamma f(z) \,dz- iA\alpha } \right\rvert} &= {\left\lvert { \int_\gamma f(z) \,dz- \int_\gamma {A\over z} \,dz} \right\rvert}\\ &= {\left\lvert {\int_\gamma f(z) - {A\over z} \,dz} \right\rvert} \\ &= {\left\lvert {\int_\gamma{zf(z) - A \over z} \,dz} \right\rvert} \\ &\leq \int_\gamma {\left\lvert {zf(z) - A \over z} \right\rvert} \,dz\\ &= \int_\gamma { {\left\lvert {zf(z) - A} \right\rvert} \over R} \,dz\\ &\leq {1\over R } \int_\gamma {\left\lVert {zf(z) - A} \right\rVert}_{\infty, \gamma} \,dz\\ &= {{\varepsilon}\over R}\cdot \mathop{\mathrm{length}}(\gamma) \\ &= {{\varepsilon}\over R} \cdot R\alpha \\ &= {\varepsilon}\alpha \\ &\overset{R\to\infty}\longrightarrow 0 .\end{align*}
Series Convergence
Fall 2020.2
^c47851
Expand \(\frac{1}{1-z^{2}}+\frac{1}{z-3}\) in a series of the form \(\sum_{-\infty}^{\infty} a_{n} z^{n}\) so it converges for
-
\(|z|<1\),
-
\(1<|z|<3\),
-
\(|z|>3\).
General strategy: each has two expansions, so just compute them all and pick appropriate ones for regions afterwards.
For \(1\over z-3\): \begin{align*} {1\over z-3} &= -{1\over 3}{1\over 1- {z\over 3}} = -{1\over 3}\sum_{k\geq 0}3^{-k}z^k && {\left\lvert {z} \right\rvert} < 3 \\ &= {1\over z} {1\over 1 - {3\over z}} = z^{-1}\sum_{k\geq 0} 3^k z^{-k} && {\left\lvert {z} \right\rvert} > 3 .\end{align*}
For \(1\over 1-z^2\): \begin{align*} {1\over 1-z^2} &= \sum_{k\geq 0} z^{2k} && {\left\lvert {z} \right\rvert} < 1 \\ &= {1\over z^2} {-1\over 1- z^{-2}} = -z^{-2}\sum_{k\geq 0}z^{-2k} && {\left\lvert {z} \right\rvert} > 1 .\end{align*}
So take \begin{align*} 0 < {\left\lvert {z} \right\rvert} < 1 && f(z) &= \sum_{k\geq 0}z^{2k} - {1\over 3}\sum_{k\geq 0} 3^{-k}z^k \\ 1 < {\left\lvert {z} \right\rvert} < 3 && f(z) &= -z^{-2} \sum_{k\geq 0}z^{-2k} - {1\over 3}\sum_{k\geq 0} 3^{-k}z^k \\ 3 < {\left\lvert {z} \right\rvert} < \infty && f(z) &= -z^{-2} \sum_{k\geq 0}z^{-2k} + z^{-1}\sum_{k\geq 0}3^k z^{-k} .\end{align*}
Spring 2020 HW 2.2
Let \(f\) be a power series centered at the origin. Prove that \(f\) has a power series expansion about any point in its disc of convergence.
- Cauchy’s integral formula: \begin{align*} f(z) = \int {f(\xi) \over \xi - z}\,d\xi .\end{align*}
Idea: use Cauchy’s integral formula to get a series in \((z-z_0)\). \begin{align*} f(z) &= \int {f(\xi) \over \xi -z} \,d\xi\\ &= \int f(\xi) \qty{ 1\over \xi - (z - z_0) - z_0 } \,d\xi\\ &= \int { f(\xi) \over\xi - z_0} \qty{ 1\over 1-w } \,d\xi&& w\coloneqq{z-z_0 \over \xi - z_0} \\ &= \int { f(\xi) \over\xi - z_0} \sum_{k\geq 0} w^k \,d\xi\\ &= \sum_{k\geq 0} \qty{\int {f(\xi) \over \xi - z_0} \,d\xi} w^k\\ &= \sum_{k\geq 0} \qty{\int {f(\xi) \over \xi - z_0} \,d\xi} w^k\\ &= \sum_{k\geq 0} \qty{\int {f(\xi) \over (\xi - z_0)^{k+1} } \,d\xi} (z-z_0)^k ,\end{align*} where we’ve integrated over a curve contained in \(D\) the disc of convergence, and that the power series for \(f\) converges uniformly on \(D\) to commute the sum and integral.
Fall 2015, Spring 2020 HW 2, Ratio Test
Let \(a_n\neq 0\) and show that \begin{align*} \lim_{n\to \infty} {{\left\lvert {a_{n+1}} \right\rvert} \over {\left\lvert {a_n} \right\rvert}} = L \implies \lim_{n\to\infty} {\left\lvert {a_n} \right\rvert}^{1\over n} = L .\end{align*}
In particular, this shows that when applicable, the ratio test can be used to calculate the radius of convergence of a power series.
Analytic on circles
Suppose \(f\) is analytic on a region \(\Omega\) such that \({\mathbb{D}}\subseteq \Omega \subseteq {\mathbb{C}}\) and \(f(z) = \sum_{n=0}^\infty a_n z^n\) is a power series with radius of convergence exactly 1.
-
Give an example of such an \(f\) that converges at every point of \(S^1\).
-
Give an example of such an \(f\) which is analytic at \(1\) but \(\sum_{n=0}^\infty a_n\) diverges.
- Prove that \(f\) can not be analytic at every point of \(S^1\).
Part a: Take \(f(z) \coloneqq\displaystyle\sum n^{-2}z^n\), which converges absolutely for \({\left\lvert {z} \right\rvert}=1\) by the comparison test.
Part b: Take \(f(z) \coloneqq{1\over 1+z} = \sum_{k\geq 0} (-1)^k z^k\), then \(f(1) = 2\) by analytic continuation of the series at \(z=1\). Then \(a_k = (-1)^k\),
Part c: ??? Not clear if this is true, take \(f(z) = \sum z^n/n^2\).
Spring 2020 HW 2.3: series on the circle
Prove the following:
-
\(\sum_{n} nz^n\) does not converge at any point of \(S^1\)
-
\(\sum_n {z^n \over n^2}\) converges at every point of \(S^1\).
- \(\sum_n {z^n \over n}\) converges at every point of \(S^1\) except \(z=1\).
-
Summation by parts: Set \(B_0 \coloneqq 0, B_n \coloneqq\sum_{k\leq n} b_k\), then \begin{align*} \sum_{n=M}^{N} a_{n} b_{n}=a_{N} B_{N}-a_{M} B_{M-1}-\sum_{n=M}^{N-1}\left(a_{n+1}-a_{n}\right) B_{n} .\end{align*}
-
Summing a geometric series: \begin{align*} \sum_{1\leq k \leq N} z^k = {1 - z^{N+1}\over 1-z} .\end{align*}
Part 1: This series does not have small tails: writing \(c_n \coloneqq n z^n\) we have \({\left\lvert {c_n} \right\rvert} = {\left\lvert {nz^n} \right\rvert} = {\left\lvert {n} \right\rvert}\to \infty\) when \({\left\lvert {z} \right\rvert} = 1\).
Part 2: This converges absolutely and absolute convergence implies convergence: \begin{align*} {\left\lvert {\sum n^{-2} z^n} \right\rvert} \leq \sum {\left\lvert {n^{-2}z^n} \right\rvert} = \sum n^{-2} < \infty .\end{align*}
Part 3: Write \(f(z) = \sum_{k\geq 1} k^{-1}z^k\). The value \(f(1)\) is the harmonic series, which we know diverges from undergraduate Calculus. For \(z\neq 1\), apply summation by parts with \(a_k \coloneqq k^{-1}\) and \(b_k \coloneqq z^k\), so
- \(a_N = N^{-1}\)
- \(a_M = M^{-1}\)
- \(B_N = \sum_{k\leq N} z^k = {1-z^{N+1} \over 1-z}\)
- \(B_M = \sum_{k\leq M} z^k\)
- \(a_{n+1} - a_n = (n+1)^{-1}+ n^{-1}= - (n(n+1))^{-1}\)
Note that \({\left\lvert {B_N} \right\rvert} \leq C_z \coloneqq{2\over {\left\lvert {1-z} \right\rvert} }\) for any \(N\), since \({\left\lvert {z} \right\rvert} = 1\) is on \(S^1\) and the maximum distance between two points on \(S^1\) is 2. Moreover \(C_z < \infty\) when \(z\neq 1\).
Applying the formula: ` \begin{align*} {\left\lvert {\sum_^N n^{-1}z^n } \right\rvert} &\leq {\left\lvert { N^{-1}B_N
- M^{-1}B_{M-1}
- \sum_^{N-1} \left[ -(n(n+1))^{-1}B_n \right] } \right\rvert}\ &\leq N^{-1}C_z + M^{-1}C_z + \sum_{M\leq n \leq N-1} C_z \qty{1\over n^2 + n}\ &\leq C_z\qty{N^{-1}+ M^{-1}+ \sum_{M\leq n \leq N-1} n^{-2}} \ &\overset{M, N\to\infty}\longrightarrow 0 ,\end{align*} `{=html} where we’ve used the triangle inequality and convergence of \(\sum n^{-2}\). By the Cauchy criterion for sums, \(f(z)\) converges pointwise for \(z\neq 1\).
Uniform convergence of series
Suppose \(\sum_{n=0}^\infty a_n z^n\) converges for some \(z_0 \neq 0\).
-
Prove that the series converges absolutely for each \(z\) with \({\left\lvert {z} \right\rvert} < {\left\lvert {z} \right\rvert}_0\).
-
Suppose \(0 < r < {\left\lvert {z_0} \right\rvert}\) and show that the series converges uniformly on \({\left\lvert {z} \right\rvert} \leq r\).
Sine series?
Prove that the following series converges uniformly on the set \(\left\{{z {~\mathrel{\Big\vert}~}\Im(z) < \ln 2}\right\}\): \begin{align*} \sum_{n=1}^\infty {\sin(nz) \over 2^n} .\end{align*} Suppose \(0 < r < {\left\lvert {z_0} \right\rvert}\) and show that the series converges uniformly on \({\left\lvert {z} \right\rvert} \leq r\).
Fall 2015 Extras
Assume \(f(z)\) is analytic in \({\mathbb D}\) and \(f(0)=0\) and is not a rotation (i.e. \(f(z) \neq e^{i \theta} z\)). Show that \(\displaystyle \sum_{n=1}^\infty f^{n}(z)\) converges uniformly to an analytic function on compact subsets of \({\mathbb D}\), where \(f^{n+1}(z) = f(f^{n}(z))\).
Holomorphicity
Fall 2019.6
^430a0a
A holomorphic mapping \(f: U \rightarrow V\) is a local bijection on \(U\) if for every \(z \in U\) there exists an open disc \(D \subset U\) centered at \(z\) so that \(f: D \rightarrow f(D)\) is a bijection. Prove that a holomorphic map \(f: U \rightarrow V\) is a local bijection if and only if \(f^{\prime}(z) \neq 0\) for all \(z \in U\).
- Inverse function theorem: if \(F\in C^1({\mathbb{R}}^n\to {\mathbb{R}}^n)\) and \(D_f\) is invertible at \(p\), the \(F\) is invertible in a neighborhood of \(p\), and \(F^{-1}\) is \(C^1\).
\(\impliedby\): Let \(z\in U\) be fixed. Since \(f\) is holomorphic at \(z\) and \(f'(z)\neq 0\), consider \(f(x, y)\) and its Jacobian as a real-valued function: \begin{align*} D_f = { \begin{bmatrix} {u_x} & {u_y} \\ {v_x} & {v_y} \end{bmatrix} } \implies \operatorname{det}(D_f) = u_x v_y - v_x u_y = u_x^2 + v_x^2 = {\left\lvert {f'} \right\rvert}^2 > 0 ,\end{align*} so the derivative matrix is invertible at \(z\). Applying the inverse function theorem yields that \(f\) is a smooth diffeomorphism on some neighborhood \(N\ni p\), and in particular is bijective on \(N\).
\(\not\impliedby\): If \(f'(z) = 0\) for some \(z\), then we claim that \(f\) can not be injective. Equivalently, injectivity of \(f\) implies \(f'\neq 0\). Suppose \(f\) is holomorphic at \(z_0\) but \(f'(z_0)=0\). Write \(h(z) \coloneqq f(z) - f(z_0)\), which has a zero \(z_0\) of some order \(k\geq 2\). For a disc \(D\) small enough about \(z_0\) avoiding the other (isolated) zeros of \(h\) and \(f'\), for any \(p\) in a neighborhood of \(z_0\) and contained in \(D\), \begin{align*} \int_{{{\partial}}D} {f'(\xi) \over f(\xi) - p} \,d\xi = {\sharp}Z(f(z) - p) ,\end{align*} using the argument principle and that \((f(\xi) - p)' = f'(\xi)\). But for \(D\) small enough, \({\sharp}Z(f(z) - p) = {\sharp}Z(f(z) - f(z_0)) = k\) by Rouché, so there are \(k\) solutions to \(f(z) = p\). Since \((f(z) - p)' \neq 0\) in \(D\), none of these can be repeated roots, so these \(k\) solutions are distinct, forcing \(f\) to be \(k\)-to-one and fail injectivity.
Expanding on the Rouché argument: set \(c \coloneqq\inf_{z\in D} {\left\lvert {f(z) - w_0} \right\rvert}\), then for \(D'\) of radius \(c\), set
- \(F(z) \coloneqq(f(z) - z_0) - (f(z) - p) = z-p\)
- \(G(z) = f(z) - z_0\)
- \((F+G)(z) = f(z) - p\)
Then \(F>G\) on \({{\partial}}D'\) will imply \(F, F+G\) have the same number of zeros within \(D'\), and this bound follows from \begin{align*} {\left\lvert {F(z)} \right\rvert} = {\left\lvert {z-p} \right\rvert} < c \leq {\left\lvert {f(z) - p } \right\rvert} ,\end{align*} where the first inequality is from making the disc small and the second from choosing \(c\) as an inf.
Spring 2020 HW 1.7
Prove that \(f(z) = {\left\lvert {z} \right\rvert}^2\) has a derivative at \(z=0\) and nowhere else.
The easy check: \(f\) is differentiable iff \({ \mkern 1.5mu\overline{\mkern-1.5mu{\partial}\mkern-1.5mu}\mkern 1.5mu}_z f = 0\), but \begin{align*} { \mkern 1.5mu\overline{\mkern-1.5mu{\partial}\mkern-1.5mu}\mkern 1.5mu}_z {\left\lvert {z} \right\rvert}^2 = { \mkern 1.5mu\overline{\mkern-1.5mu{\partial}\mkern-1.5mu}\mkern 1.5mu}_z z\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu = z \neq 0 ,\end{align*} unless of course \(z=0\).
A more explicit check: check the limits. \begin{align*} {f(z) - f(0) \over z-0} = { {\left\lvert {z} \right\rvert}^2 \over z } = {z\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu \over z} = \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu \overset{z\to 0}\longrightarrow 0 ,\end{align*} so \(f\) is differentiable at \(w=0\). Now taking \(w = Re^{i\theta} \neq 0\), \begin{align*} {f(z) -f(w) \over z-w} = {{\left\lvert {z} \right\rvert}^2 - {\left\lvert {w} \right\rvert}^2 \over z - w} = {\qty{{\left\lvert {z} \right\rvert} + {\left\lvert {w} \right\rvert} } \qty{{\left\lvert {z} \right\rvert} - {\left\lvert {w} \right\rvert}} \over z-w } = {{\left\lvert {z} \right\rvert} - {\left\lvert {w} \right\rvert} \over z-w}\cdot \qty{{\left\lvert {z} \right\rvert} + {\left\lvert {w} \right\rvert}} .\end{align*} First let \(z\to w\) along \({{\partial}}{\mathbb{D}}_{R'}(0)\) where \(R' \coloneqq{\left\lvert {w} \right\rvert}\), so that the numerator vanishes and the limit is zero. Then let \(z\to w\) along the curve \(\left\{{tw{~\mathrel{\Big\vert}~}t\in [0, 1]}\right\}\), then \({\left\lvert {z} \right\rvert} = t {\left\lvert {w} \right\rvert}\), so the ratio becomes \begin{align*} {{\left\lvert {z} \right\rvert} - {\left\lvert {w} \right\rvert} \over z-w}\cdot \qty{{\left\lvert {z} \right\rvert} + {\left\lvert {w} \right\rvert}} &= {t{\left\lvert {w} \right\rvert} - {\left\lvert {w} \right\rvert} \over tw-w}\cdot \qty{t{\left\lvert {w} \right\rvert} + {\left\lvert {w} \right\rvert}} \\ &= {{\left\lvert {w} \right\rvert}\qty{t-1 } \over w(t-1)} \cdot {\left\lvert {w} \right\rvert}(t+1) \\ &= { {\left\lvert {w} \right\rvert}^2(t+1) \over w} \\ &= \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu(t+1) \\ &\overset{t\to 1}\to 2\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu ,\end{align*} which is nonzero is \(w\neq 0\).
Spring 2020 HW 1.8
Let \(f(z)\) be analytic in a domain, and prove that \(f\) is constant if it satisfies any of the following conditions:
- \({\left\lvert {f(z)} \right\rvert}\) is constant.
- \(\Re(f(z))\) is constant.
- \(\arg(f(z))\) is constant.
- \(\mkern 1.5mu\overline{\mkern-1.5muf(z)\mkern-1.5mu}\mkern 1.5mu\) is analytic.
How do you generalize (a) and (b)?
Slick proof: use that no curve \(\gamma \subseteq {\mathbb{C}}\) is open in \({\mathbb{C}}\).
If \({\left\lvert {f} \right\rvert} = c = r^2\) for some \(r\), then the image of \(f\) is contained in the curve \({{\partial}}{\mathbb{D}}_r(0)\). Since \(f\) is holomorphic on the source domain \(\Omega\), \(f\) is an open map, so if \(f\) is nonconstant the \(f(\Omega)\) is open. But \(f(\Omega) \subseteq {{\partial}}{\mathbb{D}}_r(0)\) can not be open, so \(f\) must be constant.
The usual more direct proof: write \({\left\lvert {f(z)} \right\rvert} = u^2 = v^2 = r^2\). The claim is that both \(u\) and \(v\) are constant. Take partial derivatives and clear the factor of 2: \begin{align*} {\partial}_x: \quad uu_x + vv_x &= 0\\ {\partial}_y: \quad uu_y + vv_y &= 0 .\end{align*} Now apply CR: \(u_x= v_y, u_y=-v_x\), then \begin{align*} uu_x - vu_y &=0 \\ uu_y + vu_x &=0 .\end{align*} Multiply the first by \(u_x\) and the second by \(u_y\), then add \begin{align*} uu_x^2 - vu_y u_x &= 0 \\ uu_y^2 + vu_x u_y &=0 \\ \implies u(u_x^2 + u_y^2) &=0 .\end{align*} A similar calculation yields \(v(v_x^2 + v_y^2) = 0\), so If \(u(x,y) = v(x, y) = 0\) at any point, then \({\left\lvert {f} \right\rvert} = 0\) and \(f\equiv 0\), so we’re done. Otherwise, \(u,v\) do not simultaneously vanish, so we must have \begin{align*} 0 = u_x^2 + u_y^2 &\implies 0 = u_x = u_y \implies u \text{ constant }\\ 0 = v_x^2 + v_y^2 &\implies 0 = v_x = v_y \implies v \text{ constant } ,\end{align*} so \(f=u+iv\) is constant.
Write \(f=u+iv\), so \(u\equiv c\) is constant. Then \(u_x = u_y = 0\), and CR yields \(v_y = u_x = 0\) and \(v_y = -u_x = 0\), so \(v\) is constant, making \(f\) constant.
Slick proof: apply the open mapping theorem again, since \(\operatorname{Arg}(f) = \theta_0\) implies that \(\operatorname{im}(f) \subseteq \gamma\) for the curve \(\gamma \coloneqq\left\{{t e^{i\theta_0}{~\mathrel{\Big\vert}~}t\in {\mathbb{R}}}\right\}\) which has no open subsets.
Note that this implies that any \({\mathbb{R}}{\hbox{-}}\)valued holomorphic function is constant.
Write \(f=u+iv\) so \(\mkern 1.5mu\overline{\mkern-1.5muf\mkern-1.5mu}\mkern 1.5mu = u +i\tilde v\) where \(\tilde v \coloneqq-v\). Then \(u, \tilde v\) are constant, so in particular \(\Re(f)\) is constant and by 2 \(f\) is constant.
Spring 2020 HW 1.9
Prove that if \(z\mapsto f(z)\) is analytic, then \(z \mapsto \mkern 1.5mu\overline{\mkern-1.5muf(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu\) is analytic.
It suffices to show that \(g(z) \coloneqq\mkern 1.5mu\overline{\mkern-1.5muf(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu\) satisfies CR. Write \(f=u+iv\), then \begin{align*} g(x, y) \coloneqq a(x, y) + ib(x, y) = u(x, -y) -i v(x, -y) ,\end{align*} so we want to show \(a_x = b_y\) and \(a_y = -b_x\). By the chain rule, \begin{align*} a_x &= {\partial}_x (x\mapsto u(x, -y)) = u_x \\ a_y &= {\partial}_x (y\mapsto u(x, y))\circ(y\mapsto -y) = -u_y \\ b_x &= {\partial}_x(x\mapsto -v(x, -y)) = -v_x \\ b_y &= {\partial}_x(y \mapsto - v(x, y))\circ(y\mapsto -y) = v_y .\end{align*} Now use CR for \(f\) to write \begin{align*} a_x &= u_x = v_y = b_y \\ a_y &= -u_y = v_x = -b_x .\end{align*}
Set \(g(z) \coloneqq(f(z^*))^* \coloneqq\mkern 1.5mu\overline{\mkern-1.5muf(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu\), we can then show \(g'\) exists: \begin{align*} \lim_{h\to 0} {g(z+h) - g(z) \over h} &\coloneqq\lim_{h\to 0} {f((z+h)^*)^* - f(z^*)^* \over h^{**}} \\ &= \lim_{h\to 0} {\qty{ f(z^* + h^*) - f(z^*) }^* \over h^{**}} \\ &= \lim_{h\to 0} \qty{ f(z^* + h^* ) - f(z^*) \over h^* }^* \\ &\coloneqq\qty{f'(z^*)}^* ,\end{align*} where we’ve used that \(w\mapsto w^*\) is continuous to commute a limit. So this limit exists, \(g\) is differentiable with \(g'(z) \coloneqq\mkern 1.5mu\overline{\mkern-1.5muf'(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu\).
Since \(f\) is analytic, take a Laurent expansion \(f(z) = \sum_{k\geq 0} c_k z^k\). Then \begin{align*} g(z) \coloneqq(f(z^*))^* = \qty{\sum_{k\geq 0} c_k \mkern 1.5mu\overline{\mkern-1.5muz^k\mkern-1.5mu}\mkern 1.5mu }^* = \sum_{k\geq 0} \mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu z^k ,\end{align*} making \(g\) analytic.
Spring 2020 HW 1.10
-
Show that in polar coordinates, the Cauchy-Riemann equations take the form \begin{align*} \frac{\partial u}{\partial r}=\frac{1}{r} \frac{\partial v}{\partial \theta} \text { and } \frac{\partial v}{\partial r}=-\frac{1}{r} \frac{\partial u}{\partial \theta} .\end{align*}
-
Use (a) to show that the logarithm function, defined as \begin{align*} \operatorname{Log}z=\log r+i \theta \text { where } z=r e^{i \theta} \text { with }-\pi<\theta<\pi .\end{align*} is holomorphic on the region \(r> 0, -\pi < \theta < \pi\).
Also show that this function is not continuous in \(r>0\).
Part 1:
Write \begin{align*} x &= r\cos \theta \implies \operatorname{grad}_{r, \theta} x = {\left[ {\cos \theta, -r\sin \theta} \right]} \\ y & =r\sin \theta \implies \operatorname{grad}_{r, \theta} y = {\left[ {\sin \theta, r\cos \theta} \right]} .\end{align*} Then \begin{align*} u_r &= u_x x_r + u_y y_r \\ &= u_x \cos \theta + u_y \sin \theta \\ &= v_y \cos \theta - v_x \sin \theta \\ &= r^{-1}\qty{v_y \cdot r\cos\theta - u_y \cdot r \sin \theta} \\ &= r^{-1}\qty{v_y y_\theta + u_y x_\theta} \\ &= r^{-1}v_\theta .\end{align*} Similarly \begin{align*} v_r &= v_x x_r + v_y y_r \\ &= v_x \cos \theta + v_y \sin \theta \\ &= -u_y \cos \theta + u_x \sin \theta \\ &= -r^{-1}\qty{u_y \cdot r\cos\theta i u_x \cdot r\sin \theta } \\ &= -r^{-1}\qty{u_x x_\theta + u_y y_\theta} \\ &= -r^{-1}u_\theta .\end{align*}
Part 2:
Define \(u(r, \theta) = \log(r)\) and \(v(r, \theta) = \theta\) to write \(\operatorname{Log}(z) = u+iv\). Then check \begin{align*} u_r &= r^{-1}, \quad v_\theta = 1 \implies u_r = r^{-1}v_\theta \\ v_r &= 0, \quad u_\theta = 0 \implies v_r = -r^{-1}u_\theta ,\end{align*} provided \(r>0\) so that \(u_r\) is defined.
That this function is not continuous: let \(w_k = 1\cdot e^{i(2\pi - 1/k)}\), noting that these are two sequences converging to 1. If \(\operatorname{Log}(z)\) were continuous, we would have \begin{align*} \lim_{k\to\infty} \operatorname{Log}(w_k) = \operatorname{Log}(1) \coloneqq\log(1) + i\cdot 0 = 0 ,\end{align*} Thus for any \({\varepsilon}\) we could choose \(k\gg 1\) so that \begin{align*} {\left\lvert {\log(z_k) - 0} \right\rvert}, {\left\lvert {\log(w_k) - 0 } \right\rvert} < {\varepsilon} .\end{align*} However, \begin{align*} \log(w_k) = \log(1) + i(2\pi - 1/k) = i(2\pi - 1/k) = 2\pi i - {1\over k} > {\varepsilon} ,\end{align*} for arbitrarily large \(k\), provided we choose \({\varepsilon}\) small.
Fall 2021.1
Let \(f(z)\) be an analytic function on \(|z|<1\). Prove that \(f(z)\) is necessarily a constant if \(f(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\) is also analytic.
Let \(\tilde f(z) \coloneqq f(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\). Using that \(f\) is analytic iff its components solve Cauchy-Riemann, using that \(f, \tilde f\) are analytic, \begin{align*} u_x = v_y && u_y = -v_x \\ u_x = -v_y && u_y = v_x \\ \\ \implies 2u_x = v_y - v_y = 0 \implies u_x = 0 \\ \implies 2u_y = v_x - v_x = 0 \implies u_y = 0 \\ \implies 0 = u_y - u_y = v_x - (-v_x) = 2v_x \implies v_x = 0 \\ \implies 0 = u_x - u_x = v_y - (-v_y) = 2v_y \implies v_y = 0 ,\end{align*} so \(\operatorname{grad}u = [u_x, u_y] \equiv \mathbf{0}\) making \(u\) constant. Similarly \(\operatorname{grad}v = [v_x, v_y] = \mathbf{0}\), so \(f: {\mathbb{R}}^2\to {\mathbb{R}}\) is constant.
Holomorphic functions form an integral domain
Suppose \(D\) is a domain and \(f, g\) are analytic on \(D\).
Prove that if \(fg = 0\) on \(D\), then either \(f \equiv 0\) or \(g\equiv 0\) on \(D\).
Suppose \(fg=0\) on \(D\) but \(f\not\equiv 0\), we’ll show \(g\equiv 0\) on \(D\). Since \(f\not \equiv 0\), \(f(z_0)\neq 0\) at some point \(z_0\). Since \(f\) is holomorphic, in particular \(f\) is continuous, so there is a neighborhood \(U\ni z_0\) where \(f(z)\neq 0\) for any \(z\in U\). But \(f(z)g(z) = 0\) for all \(z\in U\), and since \({\mathbb{C}}\) is an integral domain, this forces \(g(z) = 0\) for every \(z\in U\). So \(g\equiv 0\) on \(U\). Now \(U\) is a set with a limit point, so by the identity principle, \(g\equiv 0\) on \(D\).
Holomorphic functions with specified values
Suppose \(f\) is analytic on \({\mathbb{D}}^\circ\). Determine with proof which of the following are possible:
-
\(f\qty{1\over n} = (-1)^n\) for each \(n>1\).
-
\(f\qty{1\over n} = e^{-n}\) for each even integer \(n>1\) while \(f\qty{1\over n} = 0\) for each odd integer \(n>1\).
-
\(f\qty{1\over n^2} = {1\over n}\) for each integer \(n>1\).
-
\(f\qty{1\over n} = {n-2 \over n-1}\) for each integer \(n>1\).
Part a: Not possible: if \(f\) is holomorphic then \(f\) is in particular continuous, so \begin{align*} f(0) = f(\lim 1/n) = \lim f(1/n) = \lim (-1)^n ,\end{align*} which does not converge.
Part b: Not possible: note that \(1/n\) has a limit point, so if \(f(1/n)=0\) then \(f\equiv 0\) on \({\mathbb{D}}\) by the identity principle. In particular, we can not have \(f(1/n) = e^{-n}>0\).
Alternatively, note that a holomorphic \(f\) must have isolated zeros, while \(z_0=0\) is forced to be a zero of \(f\) by continuity, which has infinitely many zeros of the form \(1/n\) in any neighborhood.
Part c: Not possible: suppose so, then by continuity, we have \begin{align*} f(0) = f(\lim 1/n^2)= \lim f(1/n^2)=\lim 1/n = 0 ,\end{align*} so \(z_0=0\) is a zero. Now defining \(g(z) = z^{1\over 2} \coloneqq e^{1\over 2 \log(z)}\) on \(U \coloneqq{\mathbb{C}}\setminus(-\infty, 0]\) extending this continuously to zero by \(g(0)= 0\) yields \(g(z) = f(z)\)on \(\left\{{1/n^2 {~\mathrel{\Big\vert}~}n>1}\right\}\cup\left\{{0}\right\}\), so \(g(z) \equiv f(z)\) on \(U\). But then \(g\equiv f\) on \({\mathbb{D}}\), and \(g\) is not holomorphic on all of \({ \mathsf{D} }\), contradicting that \(f\) was holomorphic on \({\mathbb{D}}\).
Part d: Yes: note that this forces \(f(0) = \lim {n-2\over n-1} = 1\) by continuity at \(z=0\). We can write \begin{align*} {n-2\over n-1} = {1 - 2\cdot{1\over n} \over 1 - {1\over n}} ,\end{align*} so define \(g(z) \coloneqq{1-2z\over 1-z}\). Then \(g(1/n) = f(1/n)\) for all \(n\) and \(g(0) = 1= f(0)\), so \(g=f\) on a set with an accumulation point making \(g\equiv f\) on \({\mathbb{D}}\). Note that \(g\) is holomorphic on \({\mathbb{D}}\), since it has only a simple pole at \(z_0 = 1\).
Geometry
Some Geometry
Let \(z_{k}(k=1, \cdots, n)\) be complex numbers lying on the same side of a straight line passing through the origin. Show that
\begin{align*} z_{1}+z_{2}+\cdots+z_{n} \neq 0, \quad 1 / z_{1}+1 / z_{2}+\cdots+1 / z_{n} \neq 0 \end{align*}
Hint: Consider a special situation first.
Images of circles
Let \(f(z)=z+1 / z\). Describe the images of both the circle \(|z|=r\) of radius \(r(r \neq 0)\) and the ray \(\arg z=\theta_{0}\) under \(f\) in terms of well known curves.
Geometric Identities
Prove that \(\left|z_{1}+z_{2}\right|^{2}+\left|z_{1}-z_{2}\right|^{2}=2\left(\left|z_{1}\right|^{2}+\left|z_{2}\right|^{2}\right)\) for any two complex numbers \(z_{1}, z_{2}\), and explain the geometric meaning of this identity
Geometric Identities
Use \(n\)-th roots of unity (i.e. solutions of \(z^{n}-1=0\) ) to show that
\begin{align*} \cos \frac{2 \pi}{n}+\cos \frac{4 \pi}{n}+\cos \frac{6 \pi}{n}+\cdots+\cos \frac{2(n-1) \pi}{n}+=-1 \text { and } \\ \sin \frac{2 \pi}{n}+\sin \frac{4 \pi}{n}+\sin \frac{6 \pi}{n}+\cdots \frac{2(n-1) \pi}{n}=0 \end{align*}
Hint: If \(z^{n}+c_{1} z^{n-1}+\cdots+c_{n-1} z+c_{n}=0\) has roots \(z_{1}, z_{2}, \ldots, z_{n}\), then \begin{align*} z_{1}+z_{2}+\cdots+z_{n}=-c_{1} \\ z_{1} z_{2} \cdots z_{n}=(-1)^{n} c_{n} \text { (not used) } \end{align*}
Geometry from equations
Describe each set in the \(z\)-plane in (a) and (b) below, where \(\alpha\) is a complex number and \(k\) is a positive number such that \(2|\alpha|<k\).
-
\(|z-\alpha|+|z+\alpha|=k\);
-
\(|z-\alpha|+|z+\alpha| \leq k\).
Spring 2020.1, Spring 2020 HW 1.4
^ea471a
-
Prove that if \(c>0\), \begin{align*} {\left\lvert {w_1} \right\rvert} = c{\left\lvert {w_2} \right\rvert} \implies {\left\lvert {w_1 - c^2 w_2} \right\rvert} = c{\left\lvert {w_1 - w_2} \right\rvert} .\end{align*}
-
Prove that if \(c>0\) and \(c\neq 1\), with \(z_1\neq z_2\), then the following equation represents a circle: \begin{align*} {\left\lvert {z-z_1 \over z-z_2} \right\rvert} = c .\end{align*} Find its center and radius.
Hint: use part (a)
\begin{align*} {\left\lvert {w_1 - c^2 w_2} \right\rvert}^2 &= (w_1 - c^2 w_2) ( \mkern 1.5mu\overline{\mkern-1.5muw_1\mkern-1.5mu}\mkern 1.5mu - c^2 \mkern 1.5mu\overline{\mkern-1.5muw_2\mkern-1.5mu}\mkern 1.5mu ) \\ &= {\left\lvert {w_1} \right\rvert}^2 + c^4 {\left\lvert {w_2} \right\rvert}^2 - 2c^2 \Re(w_1 \mkern 1.5mu\overline{\mkern-1.5muw_2\mkern-1.5mu}\mkern 1.5mu) \\ &= {\color{green} c^2 {\left\lvert {w_2} \right\rvert}^2 } + c^4 {\left\lvert {w_2} \right\rvert}^2 - 2c^2 \Re(w_1 \mkern 1.5mu\overline{\mkern-1.5muw_2\mkern-1.5mu}\mkern 1.5mu) \\ &= c^2 {\left\lvert {w_2} \right\rvert}^2 + {\color{green} c^2 {\left\lvert {w_1} \right\rvert}^2 } - 2c^2 \Re(w_1 \mkern 1.5mu\overline{\mkern-1.5muw_2\mkern-1.5mu}\mkern 1.5mu) \\ &= c^2 {\left\lvert {w_1 - w_2} \right\rvert} ,\end{align*} where we’ve applied the assumption \({\left\lvert {w_1} \right\rvert} = c{\left\lvert {w_2} \right\rvert}\) twice.
Using part 1: \begin{align*} w_1\coloneqq z-z_1, w_2 \coloneqq z-z_2 \implies {\left\lvert {w_1} \right\rvert} &= c{\left\lvert {w_2} \right\rvert} \\ \implies {\left\lvert {w_1 - c^2 w_2} \right\rvert} &= c {\left\lvert {w_1 - w_2} \right\rvert} \\ \implies {\left\lvert { z-z_1 - c^2 (z-z_2) } \right\rvert} &= {\left\lvert {(z-z_1) - (z-z_2)} \right\rvert} \\ \implies {\left\lvert {(1-c^2) z - z_3} \right\rvert} &= {\left\lvert { z_2 - z_1 } \right\rvert} \\ \implies {\left\lvert {z-z_4} \right\rvert} &= r ,\end{align*} where the \(z_i\) and \(r\) are all constant, so this is the equation of a circle.
Spring 2020 HW 1.1
Geometrically describe the following subsets of \({\mathbb{C}}\):
- \({\left\lvert {z-1} \right\rvert} = 1\)
- \({\left\lvert {z-1} \right\rvert} = 2{\left\lvert {z-2} \right\rvert}\)
- \(1/z = \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu\)
- \(\Re(z) = 3\)
- \(\Im(z) = a\) with \(a\in {\mathbb{R}}\).
- \(\Re(z) > a\) with \(a\in {\mathbb{R}}\).
- \({\left\lvert {z-1} \right\rvert} < 2{\left\lvert {z-2} \right\rvert}\)
-
A circle of radius 1 about \(z=1\).
-
A circle, using that Apollonius circles are characterized as the locus of distances whose ratios to some fixed points \(A, B\) are constant. To actually compute this: \begin{align*} {\left\lvert {z-1} \right\rvert}^2 &= 4{\left\lvert {z-2} \right\rvert}^2 \\ \implies (x-1)^2 + y^2 - 4\qty{(x-2)^2 + y^2 } &=0 \\ -3x^2 + 14x - 3y^2 - 15 &= 0 && \star\\ \implies x^2 - {14\over 3}x + y^2 + 5 &= 0 \\ \implies (x- {14\over 2\cdot 3})^2 - {14\over 2\cdot 3}^2 + y^2 + 5 &= 0 \\ \implies (x-{14\over 6})^2 + y^2 = \qty{2\over 3}^2 ,\end{align*} which is a circle of radius \(2/3\) with center \(\qty{{14\over 6}, 0}\). To avoid the calculation, use \begin{align*} Ax^2 + Bxy + Cy + \cdots = 0,\quad A=1, B=0, C=1 \implies \Delta \coloneqq B^2 - 4AC < 0 ,\end{align*} which is an ellipse, and since \(A=C\) it is in fact a circle.
-
\(S^1\), using that \({1\over z} = {\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu \over z\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu} = {\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu\over {\left\lvert {z} \right\rvert}^2}\) and if this equals \(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu\), then \({\left\lvert {z} \right\rvert}^2=1\). Alternatively, \(1 = \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5muz = {\left\lvert {z} \right\rvert}^2\).
-
Vertical line through \(z=3\).
-
Horizontal line through \(z=ia\).
-
Region to the right of the vertical line through \(z=a\).
-
Exterior of a circle: same calculation is (2), replacing \(=0\) with \(<0\). Note that the line marked \(\star\) involves dividing by a negative, so this flips the sign, and we get \(\cdots > \qty{2\over 3}^2\) at the end.
Fixed argument exercise
Fix \(a,b\in {\mathbb{C}}\) and \(\theta\), and describe the locus \begin{align*} \left\{{z{~\mathrel{\Big\vert}~}\operatorname{Arg}\qty{z-a\over z-b} = \theta}\right\} .\end{align*}
The geometry at hand:
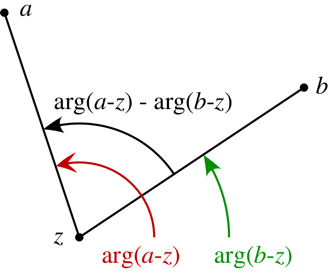
By the inscribed angle theorem, this locus is an arc of a circle whose center \(O\) is the point for which the angle \(aOb\) is \(2\theta\):
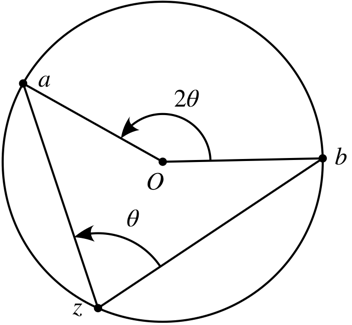
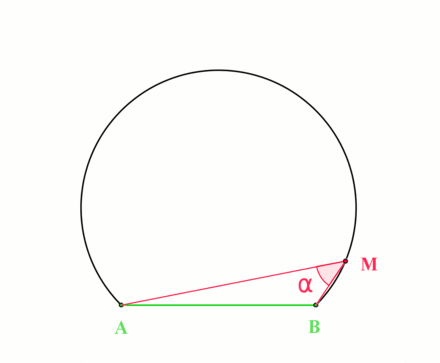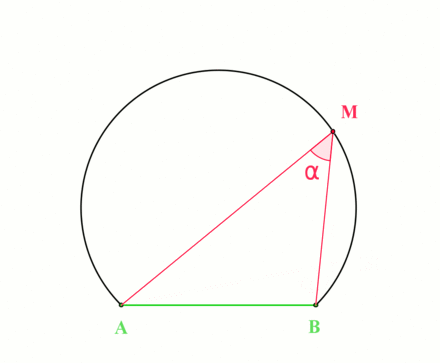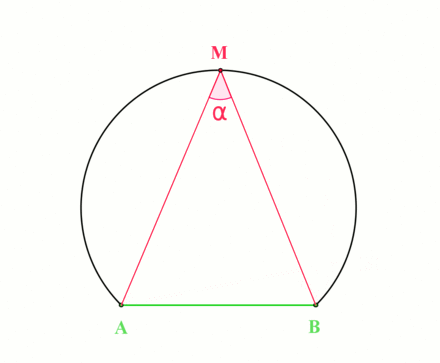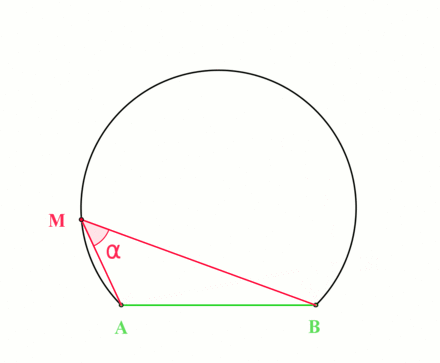
Fall 2019.2, Spring 2020 HW 1.11
^a35657
Prove that the distinct complex numbers \(z_1, z_2, z_3\) are the vertices of an equilateral triangle if and only if \begin{align*} z_{1}^{2}+z_{2}^{2}+z_{3}^{2}=z_{1} z_{2}+z_{2} z_{3}+z_{3} z_{1} .\end{align*}
\(\implies\): Write the vertices as \(z_1, z_2, z_3\) and the sides as
- \(s_1 \coloneqq z_2-z_1\)
- \(s_2 \coloneqq z_3 - z_2\)
- \(s_1 \coloneqq z_1 -z_3\)
Note that \(s_i = \pm \zeta_3 s_{i-1}\), dividing yields \begin{align*} {s_2 \over s_3} &= {s_1\over s_2} \\ &\iff s_2^2 - s_1 s_3 = 0 \\ &\iff \left(z_{2}-z_{3}\right)^{2}-\left(z_{2}-z_{1}\right)\left(z_{1}-z_{3}\right)=0 \\ &\iff \left(z_{2}^{2}+z_{3}^{2}-2 z_{2} z_{3}\right)-\left(z_{2} z_{1}-z_{2} z_{3}-z_{1}^{2}+z_{1} z_{3}\right)=0 \\ &\iff z_{1}^{2}+z_{2}^{2}+z_{3}^{2}-\left(z_{1} z_{2}+z_{2} z_{3}+z_{3} z_{1}\right)=0 .\end{align*}
\(\impliedby\): We still have \(s_i = \theta_i s_{i-1}\) for some angles \(\theta_i\) We have
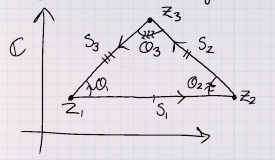
and \begin{align*} {s_1\over s_2} &= {\theta_1 \over \theta_2} \cdot {s_3\over s_1} \\ {s_2\over s_3} &= {\theta_2 \over \theta_3} \cdot {s_1\over s_2} \\ {s_3\over s_1} &= {\theta_3 \over \theta_1} \cdot {s_2\over s_3} .\end{align*}
Running the above calculation backward yields \(s_2/s_3 = s_1/s_2\), and by the 2nd equality above, this forces \(\theta_2 = \theta_3\). Similar arguments show \(\theta_1=\theta_2 = \theta_3\) which forces \(s_1=s_2 = s_3\).
Complex Arithmetic
Sum of Sines
Use de Moivre’s theorem (i.e. \(\left(e^{i \theta}\right)^{n}==\cos n \theta+i \sin n \theta\), or \(\left.(\cos \theta+i \sin \theta)^{n}=\cos n \theta+i \sin n \theta\right)\) to find the sum
\begin{align*} \sin x+\sin 2 x+\cdots+\sin n x \end{align*}
Solving Equations
Characterize positive integers \(n\) such that \((1+i)^{n}=(1-i)^{n}\)
Characters
Let \(n\) be a natural number. Show that
\begin{align*} [1 / 2(-1+\sqrt{3} i)]^{n}+[1 / 2(-1-\sqrt{3} i)]^{n} \end{align*}
is equal to 2 if \(n\) is a multiple of 3 , and it is equal to \(-1\) otherwise.
Spring 2019.3 #complex/qual/stuck
^c8872d
Let \(R>0\). Suppose \(f\) is holomorphic on \(\left\{{z{~\mathrel{\Big\vert}~}{\left\lvert {z} \right\rvert} < 3R}\right\}\). Let \begin{align*} M_{R}:=\sup _{|z| \leq R}|f(z)|, \quad N_{R}:=\sup _{|z| \leq R}\left|f^{\prime}(z)\right| \end{align*}
-
Estimate \(M_{R}\) in terms of \(N_{R}\) from above.
-
Estimate \(N_{R}\) in terms of \(M_{2 R}\) from above.
First note that by the maximum modulus principal, it suffices to consider sups on the boundary, i.e. \begin{align*} M_R = \sup_{{\left\lvert {z} \right\rvert} = R}{\left\lvert {f(z)} \right\rvert}, \qquad N_R = \sup_{{\left\lvert {z} \right\rvert} = R} {\left\lvert {f'(z)} \right\rvert} .\end{align*}
The first estimate: stuck!
The second estimate: suppose \(z_0 \in {\mathbb{D}}_R(0)\), then any \(D_R(z_0)\) is contained in \(D_{2R}(0)\), So for any such \(z_0\), apply Cauchy’s integral formula centered at \(z_0\): \begin{align*} f^{(1)}(z_0) &= {1\over 2\pi i }\oint_{{{\partial}}{\mathbb{D}}_{R}(z_0)} {f(\xi)\over (\xi-z_0)^2 }\,d\xi\\ \implies {\left\lvert { f^{(1)}(z_0)} \right\rvert} &\leq {1\over 2\pi} \oint_{{{\partial}}{\mathbb{D}}_{R}(z_0)} {\left\lvert {f(\xi)\over (\xi-z_0)^2 } \right\rvert}\,d\xi\\ &= {1\over 2\pi} \oint_{{{\partial}}{\mathbb{D}}_R(z_0)} { {\left\lvert {f(\xi)} \right\rvert} \over {\left\lvert {\xi-z_0} \right\rvert}^2 } \,d\xi\\ &= {1\over 2\pi} \oint_{{{\partial}}{\mathbb{D}}_R(z_0)} { {\left\lvert {f(\xi)} \right\rvert} \over R^2 } \,d\xi\\ &\leq {1\over 2\pi} R^{-2} \oint_{{{\partial}}{\mathbb{D}}_R(z_0)} { \sup_{z\in {{\partial}}{\mathbb{D}}_{R}(z_0) } {\left\lvert {f(z)} \right\rvert} } \,d\xi\\ &= {1\over 2\pi} R^{-2} \sup_{{{\partial}}{\mathbb{D}}_R(z_0) } {\left\lvert {f(z)} \right\rvert} \cdot 2\pi R \\ &= R^{-1}\sup_{{{\partial}}{\mathbb{D}}_R(z_0) } {\left\lvert {f(z)} \right\rvert} \\ &\leq R^{-1}M_{2R} ,\end{align*} where we’ve used in the last step that \({\mathbb{D}}_R(z_0) \subseteq {\mathbb{D}}_{2R}(0)\), and sups can only get larger when taken over larger sets. Since this was an arbitrary \(z_0\in {\mathbb{D}}_R(0)\), this holds for all \(z\) with \({\left\lvert {z} \right\rvert} \leq R\). Since taking sups preserves inequalities, we have \begin{align*} {\left\lvert {f'(z_0)} \right\rvert} \leq R^{-1}M_{2R}\, \forall {\left\lvert {z} \right\rvert} \leq R \implies N_R\coloneqq\sup_{{\left\lvert {z} \right\rvert} \leq R}{\left\lvert {f'(z)} \right\rvert} \leq R^{-1}M_{2R} .\end{align*}
Spring 2021.1
^7d0c77
The question as written on the original qual has several errors. What is below is the correct version of the inequality.
- Let \(z_{1}\) and \(z_{2}\) be two complex numbers.
-
Show that \begin{align*} \left|1-\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu_{1} z_{2}\right|^{2}-\left|z_{1}-z_{2}\right|^{2}=\left(1-\left|z_{1}\right|^{2}\right)\left(1-\left|z_{2}\right|^2\right) \end{align*}
-
Show that if \(\left|z_{1}\right|<1\) and \(\left|z_{2}\right|<1\), then \(\left|\frac{z_{1}-z_{2}}{1-\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu_{1} z_{2}}\right|<1 .\)
- Assume that \(z_{1} \neq z_{2}\). Show that \(\left|\frac{z_{1}-z_{2}}{1-\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu_{1} z_{2}}\right|=1\) if only if \(\left|z_{1}\right|=1\) or \(\left|z_{2}\right|=1\).
Part 1: For ease of notation, let \(z=z_1\) and \(w=z_2\) We want to show \begin{align*} {\left\lvert {1- z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu} \right\rvert} - {\left\lvert {z-w} \right\rvert}^2 = \qty{{1 - {\left\lvert {z} \right\rvert}^2 }} \qty{{1 - {\left\lvert {w} \right\rvert}^2}} .\end{align*}
So write \begin{align*} {\left\lvert {1- z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu} \right\rvert} - {\left\lvert {z-w} \right\rvert}^2 &= (1-z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu)(1-\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w) - (z-w)(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu) \\ &= 1 - z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu - \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w - {\left\lvert {z} \right\rvert}^2{\left\lvert {w} \right\rvert}^2 - {\left\lvert {z} \right\rvert}^2 - {\left\lvert {w} \right\rvert}^2 + w\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu + z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu \\ &= 1 - {\left\lvert {z} \right\rvert}^2{\left\lvert {w} \right\rvert}^2 - {\left\lvert {z} \right\rvert}^2 - {\left\lvert {w} \right\rvert}^2 \\ &=(1-{\left\lvert {z} \right\rvert}^2)(1-{\left\lvert {w} \right\rvert}^2) .\end{align*}
Part 2 and 3: \begin{align*} {\left\lvert {z-w \over 1 - \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w} \right\rvert}^2 \leq 1 &\iff 0 \leq {\left\lvert {1 - \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w} \right\rvert}^2 - {\left\lvert {z-w} \right\rvert}^2 \\ &\iff 0 \leq (1 - {\left\lvert {z} \right\rvert}^2 )(1 - {\left\lvert {w} \right\rvert}^2) ,\end{align*} where we’ve used part 1. But this is clearly true when \({\left\lvert {z} \right\rvert}, {\left\lvert {w} \right\rvert} < 1\), so the RHS is positive. Moreover if \({\left\lvert {z} \right\rvert} = {\left\lvert {w} \right\rvert} = 1\), the RHS is zero, yielding equalities at every step instead.
Spring 2020 HW 1.5
-
Let \(z, w \in {\mathbb{C}}\) with \(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w \neq 1\). Prove that \begin{align*} {\left\lvert {w-z \over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} < 1 \quad\text{ if } {\left\lvert {z} \right\rvert}<1,~ {\left\lvert {w} \right\rvert} < 1 \end{align*} with equality when \({\left\lvert {z} \right\rvert} = 1\) or \({\left\lvert {w} \right\rvert} = 1\).
-
Prove that for a fixed \(w\in {\mathbb{D}}\), the mapping \(F: z\mapsto {w-z \over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}\) satisfies
- \(F\) maps \({\mathbb{D}}\) to itself and is holomorphic.
- \(F(0) = w\) and \(F(w) = 0\).
- \({\left\lvert {z} \right\rvert} = 1\) implies \({\left\lvert {F(z)} \right\rvert} = 1\).
- \(F\) is a bijection.
Part 1: See Spring 2021.1 above.
Part 2, holomorphicity: This is clearly meromorphic, as it’s a rational function, and has a singularity only at \(z\) such that \(\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z = 1\). This can only happen if \(z, w \in S^1\): taking the modulus yields \begin{align*} \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z = 1 \implies {\left\lvert {w} \right\rvert}^2{\left\lvert {z} \right\rvert}^2 = 1 ,\end{align*} and moreover since \({\left\lvert {w} \right\rvert}^2 \leq 1\) and \({\left\lvert {z} \right\rvert}^2\leq 1\), the only way this product can be one is when \({\left\lvert {w} \right\rvert}^2 = {\left\lvert {z} \right\rvert}^2 = 1\). This also forces \(z=1/\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu\).
The claim is that the singularity \(1/\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu\) is removable. Note that \(1\over w = \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu\) on the circle, so \(1/\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu = \mkern 1.5mu\overline{\mkern-1.5mu\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu\mkern-1.5mu}\mkern 1.5mu = 2\), so \begin{align*} \qty{ z- \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu^{-1}} \qty{w-z \over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} &= \qty{\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z - 1 \over \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu} \qty{w-z \over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \\ &= \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu^{-1}(w-z) \\ &= w(w-z) \\ &\overset{z\to \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu^{-1}=w }\to 0 .\end{align*}
Part 2, being a bijection: This follows from finding an explicit inverse, using that \(F^2 = \operatorname{id}\): \begin{align*} F(F(z)) &= \frac{w- \qty{ \frac{w-z}{1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} } }{1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu \qty{ \frac{w-z}{1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} } } \\ &= \frac{w(1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z)-(w-z)}{q-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu(w-z)} \\ &= \frac{w-|w|^{2} z-w+z}{1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z-|w|^{2}+\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \\ &= \frac{z\left(1-|w|^{2}\right)}{1-|w|^{2}} \\ &= z .\end{align*}
Part 2, being an involution: A direct check shows that \(F(w) = 0\), since the numerator vanishes, and \(F(0) = {w - 0 \over 1 - 0} = w\).
Part 3, preserving the circle: Follows from the estimate in part 1.
Spring 2020 HW 1.2
Prove the following inequality, and explain when equality holds: \begin{align*} {\left\lvert {z-w} \right\rvert} \geq {\left\lvert { {\left\lvert {z} \right\rvert} - {\left\lvert {w} \right\rvert} } \right\rvert} .\end{align*}
\begin{align*} {\left\lvert {z-w} \right\rvert}^2 &= (z-w)(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu) \\ &= {\left\lvert {z} \right\rvert}^2 + {\left\lvert {w} \right\rvert}^2 - z\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu - \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w \\ &= {\left\lvert {z} \right\rvert}^2 + {\left\lvert {w} \right\rvert}^2 - 2\Re(\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z) \\ &\geq {\left\lvert {z} \right\rvert}^2 + {\left\lvert {w} \right\rvert}^2 - 2{\left\lvert {\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu } \right\rvert}{\left\lvert {z} \right\rvert} \\ &\geq \qty{ {\left\lvert {z} \right\rvert} - {\left\lvert {w} \right\rvert} }^2 ,\end{align*} and taking square roots introduces an absolute value on the final term. Here we’ve used the basic estimate \begin{align*} \Re(z) \leq {\left\lvert {z} \right\rvert} \implies -\Re(z) \geq -{\left\lvert {z} \right\rvert} .\end{align*}
Fall 2020.1, Spring 2020 HW 1.6
^b9b6b4
Use \(n\)th roots of unity to show that \begin{align*} 2^{n-1} \sin\qty{\pi \over n} \sin\qty{2\pi \over n} \cdots \sin\qty{(n-1)\pi \over n} = n .\end{align*}
Hint: \begin{align*} 1 - \cos(2\theta) &= 2\sin^2(\theta) \\ 2 \sin(2\theta) &= 2\sin(\theta) \cos(\theta) .\end{align*}
- \(\zeta_n \coloneqq e^{2\pi i \over n}\)
- \(\Phi_n(z) \coloneqq\prod_{1\leq j \leq n-1}(z-\zeta_n^j)\)
- \(\Phi_n(1) = n\), since \(\Phi_n(z) = {z^n-1\over z-1} = \sum_{0\leq j\leq n-1} z^j\).
- \(\sin(z) = \qty{e^{iz} - e^{-iz} \over 2i}\).
- \(\prod_k \exp(c_k) = \exp\qty{\sum_k c_k}\).
\begin{align*} \prod_{1\leq k \leq n-1} \sin\qty{k\pi\over n} &= \prod_{1\leq k \leq n-1} {\omega_n^k - \omega_n^{-k} \over 2i} \\ &= \qty{1\over 2i}^{n-1} \prod_{1\leq k \leq n-1} \omega_n^{k} \qty{1 - \zeta_n^{-k}} \\ &= \qty{1\over 2i}^{n-1} \prod_{1\leq k \leq n-1} \exp\qty{i\pi k\over n} \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{-k}} \\ &= \qty{1\over 2i}^{n-1} \exp\qty{ {i\pi\over n} \displaystyle\sum_{1\leq k \leq n-1} k } \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{-k}} \\ &= \qty{1\over 2i}^{n-1} e^{i\pi n(n-1)\over 2n} \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{-k}} \\ &= \qty{1\over 2}^{n-1}\qty{1\over i}^{n-1} \qty{ e^{i\pi \over 2} }^{n-1} \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{-k}} \\ &= 2^{1-n} \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{-k}} \\ &= 2^{1-n} \prod_{1\leq k \leq n-1} \qty{1 - \zeta_n^{k}} \\ &= 2^{1-n} { \Phi_n(z) \over z-1}\Big|_{z=1} \\ &= 2^{1-n} \qty{ \sum_{0\leq k \leq n-1} z^k}\Big|_{z=1} \\ &= n2^{1-n} .\end{align*}
\begin{align*} \prod_{1\leq j\leq n-1} \sin \left(\frac{j \pi}{n}\right) &=\prod_{1\leq j\leq n-1} \frac{1}{2 i} \qty{\zeta_n^{j\over 2} - \zeta_n^{- {j \over 2} }} \\ &=\left(\frac{1}{2 i}\right)^{n-1} \prod_{1\leq j\leq n-1} \zeta_n^{j\over 2} \prod_{1\leq j \leq n-1} \qty{1 - \zeta_n^{-j}} \\ &=\left(\frac{1}{2 i}\right)^{n-1} \prod_{1\leq j\leq n-1} \exp\qty{ij\pi \over n} \prod_{1\leq j \leq n-1} \qty{1 - \zeta_n^{-j}} \\ &=\left(\frac{1}{2 i}\right)^{n-1} \exp \left(\sum_{1\leq j\leq n-1} \frac{i j \pi}{n}\right) \Phi_{n}(1)\\ &=\left(\frac{1}{2 i}\right)^{n-1} \exp \left(\frac{(n-1) i \pi}{2}\right) \Phi_{n}(1)\\ &=\left(\frac{1}{2 i}\right)^{n-1}\left(e^{i \pi / 2}\right)^{n-1} \Phi_{n}(1)\\ &=\left(\frac{1}{2 i}\right)^{n-1} i^{n-1} \Phi_{n}(1)\\ &=\left(\frac{1}{2}\right)^{n-1} \Phi_{n}(1)\\ &=\frac{n}{2^{n-1}} .\end{align*}
Spring 2020 HW 1.5
-
Let \(z, w \in {\mathbb{C}}\) with \(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w \neq 1\). Prove that \begin{align*} {\left\lvert {w-z \over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} < 1 \quad\text{ if } {\left\lvert {z} \right\rvert}<1,~ {\left\lvert {w} \right\rvert} < 1 \end{align*} with equality when \({\left\lvert {z} \right\rvert} = 1\) or \({\left\lvert {w} \right\rvert} = 1\).
-
Prove that for a fixed \(w\in {\mathbb{D}}\), the mapping \(F: z\mapsto {w-z \over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}\) satisfies
- \(F\) maps \({\mathbb{D}}\) to itself and is holomorphic.
- \(F(0) = w\) and \(F(w) = 0\).
- \({\left\lvert {z} \right\rvert} = 1\) implies \({\left\lvert {F(z)} \right\rvert} = 1\).
\begin{align*} 0 &\leq (1 - {\left\lvert {w} \right\rvert}^2)(1-{\left\lvert {z} \right\rvert}^2) \\ \implies {\left\lvert {w} \right\rvert}^2 + {\left\lvert {z} \right\rvert}^2 &\leq 1 + {\left\lvert {w} \right\rvert}^2 {\left\lvert {z} \right\rvert}^2 \\ \implies {\left\lvert {w} \right\rvert}^2 + {\left\lvert {z} \right\rvert}^2 - 2\Re(\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z) &\leq 1 + {\left\lvert {w} \right\rvert}^2 {\left\lvert {z} \right\rvert}^2 - 2\Re(\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z) \\ \implies {\left\lvert {w-z} \right\rvert}^2 &\leq {\left\lvert {1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5muz} \right\rvert}^2 .\end{align*} Note that if either \({\left\lvert {w} \right\rvert}^2 = 1\) or \({\left\lvert {z} \right\rvert}^2 = 1\) then the first line is an equality, yielding equality in the final line.
-
That \(F: {\mathbb{D}}\to {\mathbb{D}}\): follows from the inequality, since \({\left\lvert {z} \right\rvert}, {\left\lvert {w} \right\rvert} < 1\) for \(z,w\in {\mathbb{D}}\). Holomorphicity: follows from the fact that rational expressions of holomorphic functions are holomorphic away from where the denominators vanish.
-
Then just note that \({\left\lvert {\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} \leq {\left\lvert {w} \right\rvert}{\left\lvert {z} \right\rvert} < 1\), so \({\left\lvert {1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} > 0\).
-
\(F(0) = {w-0 \over 1-0} = w\)
-
\(F(w) = {w-w\over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu w} = 0\)
-
\({\left\lvert {z} \right\rvert} = 1\) yields equality in part 1.
Other notes: \(F\) is bijective on \({\mathbb{D}}\): \begin{align*} F(F(z)) &= {w - \qty{w-z\over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu\qty{w-z\over 1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} } \\ &= {w(1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z) - (w-z) \over (1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z) - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu (w-z)} \\ &= {z-{\left\lvert {w} \right\rvert}^2 z \over 1 - {\left\lvert {w} \right\rvert}^2 }\\ &= z .\end{align*}
Laurent Expansions
Tie, Spring 2015:
Let \(\displaystyle f(z) = \frac{1}{z} + \frac{1}{z^2 -1}\). Find all the Laurent series of \(f\) and describe the largest annuli in which these series are valid.
1
Find the Laurent expansion of \begin{align*} f(z) = {z + 1 \over z(z-1)} \end{align*} about \(z=0\) and \(z=1\) respectively.
\hfill
\hfill
Let \(f(z) = {z+1\over z(z-1)}\).
About \(z=0\):
\begin{align*} f(z) &= (z+1) \qty{- {1 \over z} + {1\over z-1} } \\ &= -(z+1) \qty{{1\over z} + \sum_{n=0}^\infty z^n } \\ &= -(z+1)\sum_{n=-1}^\infty z^n \\ &= {1\over z} + 2\sum_{n=0}^\infty z^n \\ &= -{1\over z} -2 - 2z - 2z^2 - \cdots .\end{align*}
About \(z=1\):
\begin{align*} f(z) &= \qty{(1-z) -2 \over 1-z} \qty{1 \over 1 - (1-z)} \\ &= \qty{1 - {2\over 1-z}} \sum_{n=0}^\infty (1-z)^n \\ &= \sum_{n=0}^\infty (1-z)^n - 2 \sum_{n=-1}^\infty (1-z)^n \\ &= -{2\over 1-z} - \sum_{n=0}^\infty (1-z)^n \\ &= {2\over z-1} + \sum_{n=0}^\infty (-1)^{n+1} (z-1)^n \\ &= {2\over z-1} - 1 + (z-1) - (z-1)^2 + \cdots .\end{align*}
2
Find the Laurent expansions about \(z=0\) of the following functions: \begin{align*} e^{1\over z} \hspace{8em} \cos \qty{1\over z} .\end{align*}
\hfill
\hfill
Let \(f(z) = {z+1\over z(z-1)}\).
About \(z=0\):
\begin{align*} f(z) &= (z+1) \qty{- {1 \over z} + {1\over z-1} } \\ &= -(z+1) \qty{{1\over z} + \sum_{n=0}^\infty z^n } \\ &= -(z+1)\sum_{n=-1}^\infty z^n \\ &= {1\over z} + 2\sum_{n=0}^\infty z^n \\ &= -{1\over z} -2 - 2z - 2z^2 - \cdots .\end{align*}
About \(z=1\):
\begin{align*} f(z) &= \qty{(1-z) -2 \over 1-z} \qty{1 \over 1 - (1-z)} \\ &= \qty{1 - {2\over 1-z}} \sum_{n=0}^\infty (1-z)^n \\ &= \sum_{n=0}^\infty (1-z)^n - 2 \sum_{n=-1}^\infty (1-z)^n \\ &= -{2\over 1-z} - \sum_{n=0}^\infty (1-z)^n \\ &= {2\over z-1} + \sum_{n=0}^\infty (-1)^{n+1} (z-1)^n \\ &= {2\over z-1} - 1 + (z-1) - (z-1)^2 + \cdots .\end{align*}
3
Find the Laurent expansion of \begin{align*} f(z) = {z+1 \over z(z-1)^2} \end{align*} about \(z=0\) and \(z=1\) respectively.
Hint: recall that power series can be differentiated.
4
For the following functions, find the Laurent series about \(0\) and classify their singularities there: \begin{align*} {\sin^2(z) \over z} \\ z \exp{1\over z^2} \\ {1 \over z(4-z)} .\end{align*}
Tie’s Extra Questions: Fall 2015
Expand the following functions into Laurent series in the indicated regions:
-
\(\displaystyle f(z) = \frac{z^2 - 1}{ (z+2)(z+3)}, \; \; 2 < |z| < 3\), \(3 < |z| < + \infty\).
-
\(\displaystyle f(z) = \sin \frac{z}{1-z}, \; \; 0 < |z-1| < + \infty\)
Tie, Fall 2015: Laurent Coefficients
Suppose that \(f\) is holomorphic in an open set containing the closed unit disc, except for a pole at \(z_0\) on the unit circle. Let \(\displaystyle f(z) = \sum_{n = 1}^\infty c_n z^n\) denote the the power series in the open disc. Show that
-
\(c_n \neq 0\) for all large enough \(n\)’s, and
-
\(\displaystyle \lim_{n \rightarrow \infty} \frac{c_n}{c_{n+1}}= z_0\).
Spring 2020 HW 2, SS 2.6.14
Suppose that \(f\) is holomorphic in an open set containing \({\mathbb{D}}\) except for a pole \(z_0 \in {{\partial}}{\mathbb{D}}\). Let \(\sum_{n=0}^\infty a_n z^n\) be the power series expansion of \(f\) in \({\mathbb{D}}\), and show that \(\lim \frac{a_n}{a_{n+1}} = z_0\).
2
Suppose \(f\) is entire and has Taylor series \(\sum a_n z^n\) about 0.
-
Express \(a_n\) as a contour integral along the circle \({\left\lvert {z} \right\rvert} = R\).
-
Apply (a) to show that the above Taylor series converges uniformly on every bounded subset of \({\mathbb{C}}\).
- Determine those functions \(f\) for which the above Taylor series converges uniformly on all of \({\mathbb{C}}\).
Spring 2020 HW 2.4
Without using Cauchy’s integral formula, show that if \({\left\lvert {a} \right\rvert} < r < {\left\lvert {b} \right\rvert}\), then \begin{align*} \int_{\gamma} \frac{d z}{(z-\alpha)(z-\beta)} =\frac{2 \pi i}{\alpha-\beta} \end{align*} where \(\gamma\) denotes the circle centered at the origin of radius \(r\) with positive orientation.
Hint: take a Laurent expansion.
Spring 2020 HW 3 # 1
Prove that if \(f\) has two Laurent series expansions, \begin{align*} f(z) = \sum c_n(z-a)^n \quad\text{and}\quad f(z) = \sum c_n'(z-a)^n \end{align*} then \(c_n = c_n'\).
Spring 2020 HW 3 # 2
Find Laurent series expansions of \begin{align*} \frac{1}{1-z^2} + \frac{1}{3-z} \end{align*} How many such expansions are there? In what domains are each valid?
Singularities
Spring 2020 HW 3.3
Let \(P, Q\) be polynomials with no common zeros. Assume \(a\) is a root of \(Q\). Find the principal part of \(P/Q\) at \(z=a\) in terms of \(P\) and \(Q\) if \(a\) is
- a simple root, and
- a double root.
Write \begin{align*} P(z) &= \prod_{k\leq n} (z-a_k) \\ Q(z) &= \prod_{k\leq m}(z-b_k) \\ Q_j(z) &= \prod_{k\neq j}(z-b_k) = {Q(z) \over z-z_j} .\end{align*}
For \(b_\ell\) a simple pole, \begin{align*} {P(z) \over Q(z) } = {1\over z-b_\ell} {P(z) \over Q_\ell(z)} &= {1\over z-b_\ell}\qty{c_0 + c_1(z-b_\ell) + c_2(z-b_\ell)^2 + \cdots} \\ &= {c_0 \over z-b_\ell} + c_1 + { \mathsf{O}} (z-b_\ell) \\ & \coloneqq{P_{b_\ell}(z)} + c_1 + { \mathsf{O}} (z-b_\ell) ,\end{align*} so the principal part at \(z=z_\ell\) is given by \begin{align*} P_{z_\ell}(z) = {c_0 \over z-b_\ell} = {P(z) \over Q_\ell(z)}\Big|_{z=b_\ell} = \lim_{z\to z_\ell} {(z-b_\ell) P(z) \over Q(z)} .\end{align*}
For \(b_\ell\) a double pole, \begin{align*} {P(z) \over Q(z) } &= {1\over (z-b_\ell)^2 } {(z-z_\ell)^2P(z) \over Q(z) } \\ &= {1\over (z-b_\ell)^2}\qty{ d_0 + d_1(z-b_\ell) + d_2(z-b_\ell)^2 } \\ &= {d_0 \over (z-b_\ell)^2} + {d_1\over z-z_\ell} + d_2 + { \mathsf{O}} (z-b_\ell) \\ &\coloneqq P_{b_\ell}(z) + d_2 + { \mathsf{O}} (z-b_\ell) .\end{align*} To extract the \(d_1\) coefficient, note that \begin{align*} {(z-b_\ell)^2 P(z) \over Q(z)} &= d_0 + d_1(z-b_\ell) + \cdots \\ \implies {\frac{\partial }{\partial z}\,} {(z-b_\ell)^2 P(z) \over Q(z)} &= d_1 + 2d_2(z-b_\ell) + \cdots ,\end{align*} so \begin{align*} d_0 &= \lim_{z\to b_\ell} { (z-b_\ell)^2 P(z) \over Q(z) } \\ d_1 &= \lim_{z\to b_\ell} {\frac{\partial }{\partial z}\,} {(z-b_\ell)^2 P(z) \over Q(z) } \\ P_{b_\ell} &= {d_0 \over (z-b_\ell)^2} + {d_1\over z-b_\ell} .\end{align*}
Spring 2020.4
^4bd9ee
Suppose that \(f\) is holomorphic in an open set containing the closed unit disc, except for a simple pole at \(z=1\). Let \(f(z)=\sum_{n=1}^{\infty} c_{n} z^{n}\) denote the power series in the open unit disc. Show that \begin{align*} \lim _{n \rightarrow \infty} c_{n}=-\lim _{z \rightarrow 1}(z-1) f(z) .\end{align*}
Compute the series expansion of the RHS: \begin{align*} (z-1) f(z) &= (z-1) \sum_{n\geq 1} c_n z^k \\ &= -c_1z + \sum_{n\geq 2} (c_{n-1} - c_n) z^n \\ &\overset{z\to 1}\longrightarrow -c_1 + \sum_{n\geq 2} c_{n-1} - c_n \\ &\coloneqq\lim_{N\to\infty} -c_1 z + \sum_{n=2}^N c_{n-1} - c_n \\ &= \lim_{N\to\infty} -c_N ,\end{align*} where we’ve used that the sum is telescoping.
Entire functions with poles at \(\infty\)
Find all entire functions with have poles at \(\infty\).
If \(f\) is entire, write \(f(z) = \sum_{k\geq 0}c_k z^k\) and \(g(z) \coloneqq f(1/z) = \sum_{k\geq 0}c_k z^{-k}\). If \(z=\infty\) is a pole of order \(m\) of \(f\), \(z=0\) is a pole of order \(m\) of \(g\), so \begin{align*} g(z) = \sum_{0\leq k \leq m}c_k z^{-k} \implies f(z) = \sum_{0\leq k \leq m}c_k z^k ,\end{align*} making \(f\) a polynomial of degree at most \(m\).
Functions with specified poles (including at \(\infty\))
Find all functions on the Riemann sphere that have a simple pole at \(z=2\) and a double pole at \(z=\infty\), but are analytic elsewhere.
Write \(f(z) = P_2(z) + g(z)\) where \(P_2\) is the principal part of \(f\) at \(z=2\) and \(g\) is holomorphic at \(z=2\). Then \(g\) is an entire function with a double pole at \(\infty\), and is thus a polynomial of degree at most \(2\), so \(g(z) = c_2z^2 + c_1 z + c_0\). Since the pole of \(f\) at \(z=2\) is simple, \(P_2(z) = \sum_{k\geq -1} d_k (z-2)^k\). Combining these, we can write \begin{align*} f(z) = d_{-1}(z-2)^{-1}+ \sum_{0\leq k\leq 3} (d_k + c_k)(z-2)^k + \sum_{k\geq 3}d_k (z-2)^k .\end{align*} However, if \(d_k\neq 0\) for any \(k\geq 3\), this results in a higher order pole at \(\infty\), so \(f\) must be of the form \begin{align*} f(z) = d_{-1}(z-2)^{-1}+ \sum_{0\leq k\leq 3} (d_k + c_k)(z-2)^k .\end{align*}
Entire functions with singularities at \(\infty\)
Let \(f\) be entire, and discuss (with proofs and examples) the types of singularities \(f\) might have (removable, pole, or essential) at \(z=\infty\) in the following cases:
- \(f\) has at most finitely many zeros in \({\mathbb{C}}\).
- \(f\) has infinitely many zeros in \({\mathbb{C}}\).
Write \(f(z) = \sum_{k\geq 0} c_k z^k\) since it is entire.
-
If \(f\) has finitely many zeros, \(f\) is nonconstant and entire, and thus unbounded by Liouville. If \(f\) is nonconstant, \(z=\infty\) can not be removable, since this would force \(f\) to be constant. So \(z=\infty\) can be a pole or an essential singularity. Both possibilities can occur: if \(f\) is a polynomial, it is entire with finitely many zeros and a pole at \(z=\infty\). Taking \(f(z)= e^z\) has no zeros and an essential singularity at \(z=\infty\).
-
If \(f\) has infinitely many zeros, if \(f\) is nonconstant then infinitely many \(c_k\) are nonzero – otherwise \(f\) is a polynomial and can only have finitely many zeros. Then \(g(z) \coloneqq f(1/z) = \sum_{k\geq 0}{c_k\over z^k}\) has infinitely many nonzero terms, making \(z=0\) an essential singularity for \(g\) and \(z=\infty\) essential for \(f\).
Sum formula for \(\sin^2\)
Define \begin{align*} f(z) &= {\pi^2 \over \sin^2 \qty{\pi z} } \\ g(z) &= \sum_{n\in {\mathbb{Z}}} {1\over (z-n)^2} .\end{align*}
- Show that \(f\) and \(g\) have the same singularities in \({\mathbb{C}}\).
- Show that \(f\) and \(g\) have the same singular parts at each of their singularities.
- Show that \(f, g\) each have period one and approach zero uniformly on \(0\leq x \leq 1\) as \({\left\lvert {y} \right\rvert}\to \infty\).
- Conclude that \(f = g\).
Part 1: This is clear: \(\sin^2(\pi z) = 0 \iff z = k\) for \(k\in {\mathbb{Z}}\), and this is a pole of order 2 for \(f\). Every \(k\in {\mathbb{Z}}\) is visibly an order 2 pole of \(g\).
Part 2: By periodicity, it suffices to consider the singularity at \(z_0 = 0\). Expanding \(\sin(\pi z) = \pi z - {1\over 3!}(\pi z)^3 + {1\over 5!} (\pi z)^5 + \cdots\) and considering \(\sin(\pi z)^2\) shows that \(z=0\) is a pole of order 2. So \(z^2f(z)\) has a removable singularity at \(z=0\), and can be expanded: \begin{align*} z^2f(z) &= \qty{\pi z\over \sin(\pi z)}^2 \\ &= (\pi z)^2 \qty{ (\pi z) ^{-1}+ {1\over 3!}(\pi z) + {7\over 360} (\pi z^3) + \cdots}^2 \\ &= (\pi z)^2 \qty{ (\pi z)^{-2} + { \mathsf{O}} (1) } \\ &= 1 + { \mathsf{O}} (z^2) \\ \implies f(z) &= z^{-2} + { \mathsf{O}} (1) ,\end{align*} so the singular part of \(f\) at \(z=0\) is \(z^{-2}\). This coincides with the \({1\over z^2}\) term in \(g\). The remaining principal parts at \(z=k\) are \({1\over (z-k)^2},\) using the fact that \(f(z+1) = f(z)\), so \(f(k) = f(0)\) and the Laurent expansions are gotten by substituting \(z-k\) in for \(z\) everywhere.
Part 3: Periodicity is clear for \(f\). For \(g\), \begin{align*} g(z+1) = \sum_{k\in {\mathbb{Z}}} ((z-1)-k)^{-2} = \sum_{k'\in {\mathbb{Z}}} (z-k)^{-2} ,\end{align*} where \(k' \coloneqq k+1\), and the equality is true since both sums run over all of \({\mathbb{Z}}\).
For convergence: take \(z=it\), then for \(f\) \begin{align*} f(it) \sim \csc^2(i\pi t) &\sim \qty{ e^{i\pi (it) } - e^{-i\pi (it)}}^{-2} \\ &= \qty{e^{-\pi t} - e^{\pi t}}^{-2} \\ &\leq {1\over e^{-\pi t} + e^{\pi t} } \\ &\sim e^{-\pi t} \\ &\to 0 ,\end{align*} using the reverse triangle inequality and that the \(e^{-\pi t}\) term in the denominator is negligible for large \(t\).
For \(g\), \begin{align*} g(it) &\sim t^{-2} + \sum_{k\geq 1} (t^2 + k^2)^{-1}\\ &\leq t^{-2} + \sum_{1\leq k \leq N}(t^2 + k^2)^{-1}+ \sum_{k\geq N}(t^2 + k^2)^{-1}\\ &\leq t^{-2} + \sum_{1\leq k \leq N}(t\cdot k^2)^{-1}+ \sum_{k\geq N}(k^2)^{-1}\\ &\leq t^{-2} + t^{-1}\sum_{1\leq k \leq N}(k^2)^{-1}+ \sum_{k\geq N}(k^2)^{-1}\\ &\overset{N\to\infty\implies t\to\infty}\longrightarrow 0 ,\end{align*} where given \(N\) we can pick \(t\) large enough so that \(t^2 + k^2 \geq tk^2\) for all \(k\leq N\). These converge to zero as \(N\to\infty\) since \(\sum k^{-2} < \infty\), making the last term the tail of a convergent sum.
Part 4: Since \(f,g\) uniformly converge to zero on the strip \(0<\Re(x) < 1\), they are bounded on this strip. Since this is a fundamental domain for their periods, they are bounded on \({\mathbb{C}}\). Write \(h\coloneqq f-g\), then \(h\) is entire since \(f,g\) have the same singular parts, and bounded since \({\left\lvert {h} \right\rvert}\leq {\left\lvert {f} \right\rvert} + {\left\lvert {g} \right\rvert}\). By Liouville, \(h\) is constant with \(\lim_{t\to\infty} h(it) = 0\), so \(h\equiv 0\) and \(f\equiv g\).
Spring 2020 HW 3.4, Tie’s Extra Questions: Fall 2015
Let \(f(z)\) be a non-constant analytic function in \(|z|>0\) such that \(f(z_n) = 0\) for infinite many points \(z_n\) with \(\lim_{n \rightarrow \infty} z_n =0\).
Show that \(z=0\) is an essential singularity for \(f(z)\).
Hint: an example of such a function is \(f(z) = \sin (1/z)\).
Note that \(z=0\) can not be a removable singularity, since then \(f\) would extend to a holomorphic function over \(z=0\), and by continuity \(0 = \lim f(z_n) = f(\lim z_n) = f(0)\). By the identity principle, this would force \(f\equiv 0\), contradicting that \(f\) is nonconstant.
It can not be a pole, because then \(f(z_n)\to \infty\), but \({\left\lvert {f(z_n)} \right\rvert} = 0 < {\varepsilon}\) for any \({\varepsilon}\) infinitely many times.
Computing Integrals
Rational, wedge
Fall 2021.3
^1eefcc
Suppose \(n \geq 2\). Use a wedge of angle \(\frac{2 \pi}{n}\) to evaluate the integral \begin{align*} I=\int_{0}^{\infty} \frac{1}{1+x^{n}} d x \end{align*}
By the ML estimate, \(\int_{C_R} f \to 0\).
The residue contribution: note the simple pole at \(\omega_n \coloneqq e^{i\pi \over n}\), \begin{align*} \mathop{\mathrm{Res}}_{z=\omega_n} f(z) = {1\over n\omega_n^{n-1}} = {\omega \over n\omega^n} = -{\omega_n \over n} .\end{align*}
The segment contributions: \(\int_{\gamma_1}f\to I\), and \begin{align*} \int_{\gamma_2}f(z) \,dz= \int_\infty^0 {1\over 1 + (\zeta_nt)^n} \zeta_n \,dt= -\zeta_n I ,\end{align*} so the contour contributions sum to \((1-\zeta_n)I\).
Solving: \begin{align*} I = -{2\pi i \omega_n\over n(1-\zeta_n)} = -2\pi i {1\over \omega_n^{-1}- \omega_n} = -2\pi i {1\over 2i \sin\qty{\pi \over n}} = {\pi \over n} \csc\qty{\pi \over n} .\end{align*}
Write \(\omega_{n, k} = \exp\qty{(2k+1)i\pi \over n}\) and factor \(z^n+1\) as \begin{align*} z^n+1 = \prod_{1\leq k \leq n}(z-\omega_{n, k}) = (z-e^{i\pi \over n})(z-e^{3i\pi \over n}) \cdots (z-e^{(2n-1)i\pi \over n}) .\end{align*} Note that only the root \(e^{i\pi\over n}\) lies in the \(2\pi/n\) wedge, so it is the only (simple) pole of \(f(z) \coloneqq{1\over 1+z^n}\) in this region. Since the pole is simple, we can compute the residue easily. Write \(r_0 \coloneqq e^{e\pi\over n}\), then By L’Hopital, \begin{align*} \mathop{\mathrm{Res}}_{z = r_0} {1\over 1+z^n} &= \lim_{z\to r_0} {z-r_0 \over 1 + z^n} \\ &= \lim_{z\to r_0} {1\over nz^{n-1}} \\ &= {1\over nr_0^{n-1}} \\ &= {1\over n e^{i\pi (n-1) \over n}} \\ &= n^{-1}{\exp\qty{-i\pi (n-1)\over n }} .\end{align*}
Take a contour \(\Gamma\) comprised of
- \(\gamma_1 = [0, R] \subseteq {\mathbb{R}}\)
- \(\gamma_2 = \left\{{Re^{it} {~\mathrel{\Big\vert}~}t\in [0, 2\pi/n]}\right\}\)
- \(\gamma_3 = \zeta_n [0, R]\)
By the residue theorem \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=r_0} f(z) = I \coloneqq\int_\Gamma f = \qty{\int_{\gamma_1} + \int_{\gamma_2} + \int_{\gamma_3}}f .\end{align*}
Taking orientations into account, \begin{align*} \int_{\gamma_3} f = -\zeta_n \int_{\gamma_1} f .\end{align*}
\begin{align*} \int_{\gamma_2}f\overset{R\to\infty}\longrightarrow 0 .\end{align*}
so in the limit we have \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=r_0}f(z) &= \qty{1 - \zeta_n}\int_{\gamma_1}f \\ \implies \int_{\gamma_1} f &= {2\pi i \mathop{\mathrm{Res}}_{z=r_0}f(z) \over 1 - \zeta_n}\\ &= {2\pi i e^{-\pi (n-1) \over n} \over n\qty{1-e^{2\pi i \over n}}} \\ &= {2\pi i \over n} \left[ e^{i\pi} e^{-i\pi \over n}\qty{1 - e^{2\pi i \over n}} \right]^{-1}\\ &= {2\pi i \over n} \left[ -1\qty{e^{-i\pi \over n} - e^{\pi i \over n}} \right]^{-1}\\ &= {2\pi i \over n} \left[ 2i \sin\qty{\pi\over n} \right]^{-1}\\ &= {\pi \over n\sin\qty{\pi \over n}} .\end{align*}
Parameterize the curves:
- \(\gamma_1 \coloneqq\left\{{t {~\mathrel{\Big\vert}~}t\in [0, R]}\right\}, \,dz= \,dt\)
- \(\gamma_3 \coloneqq\left\{{t\zeta_n {~\mathrel{\Big\vert}~}t\in [0, R]}\right\}, \,dz= \zeta_n \,dt\)
Then, a direct check: \begin{align*} \int_{\gamma_3}f(z) \,dz &= \int_0^R {1\over 1 + (\zeta_n t)^n}\zeta_n \,dt\\ &= \zeta_n\int_0^R {1\over 1 + t^n}\,dt\\ &= \zeta_n \int_{\gamma_1}f(z) \,dz .\end{align*}
Parameterize \(\gamma_2 = \left\{{Re^{it} {~\mathrel{\Big\vert}~}t\in [0, 2\pi/n]}\right\}\) and apply the ML estimate: \begin{align*} {1\over 1 + (Re^{it})^n} \leq {1\over R^n - 1} \implies \int_{\gamma_2}f \leq {1\over R^n - 1} \qty{{2\pi R \over n}} = { \mathsf{O}} (R^{n-1})\overset{R\to\infty}\longrightarrow 0 .\end{align*}
Spring 2020 HW 3, SS 3.8.2
Evaluate the integral \begin{align*} \int_\mathbb{R} {dx \over 1 + x^4} .\end{align*}
What are the poles of \({1\over 1 + z^4}\) ?
Spring 2020 HW 3, SS 3.8.6
Show that \begin{align*} \int_{-\infty}^{\infty} \frac{d x}{\left(1+x^{2}\right)^{n+1}}=\frac{1 \cdot 3 \cdot 5 \cdots(2 n-1)}{2 \cdot 4 \cdot 6 \cdots(2 n)} \cdot \pi .\end{align*}
Quadratic over quartic
Let \(a>0\) and calculate \begin{align*} \int_0^\infty {x^2 \over (x^2 + a^2)^2} \, dx .\end{align*}
Rational function
Calculate \begin{align*} \int_{-\infty}^\infty {1+x^2 \over 1+x^4}\, dx .\end{align*}
Denominator polynomial
Calculate \begin{align*} \int_0^\infty {1 \over (1+z)^2 (z+9x^2)} \, dx .\end{align*}
Rational, branch cut
Standard example
Show that \begin{align*} \int_{{\mathbb{R}}_{\geq 0}}{x^{-s} \over x+1} = {\pi \over \sin(\pi s)} .\end{align*}
Sketch: see here.
Fall 2019.1
^d9cb99
Show that \begin{align*} \int_{0}^{\infty} \frac{x^{a-1}}{1+x^{n}} d x=\frac{\pi}{n \sin \frac{a \pi}{n}} \end{align*} using complex analysis, \(0<a<n\). Here \(n\) is a positive integer.
Spring 2020 HW 3.7
Let \(0<a<4\) and evaluate \begin{align*} \int_0^\infty \frac{x^{\alpha-1}}{1+x^3} ~dx \end{align*}
Tie’s Extra Questions: Fall 2011, Spring 2015
Show that \begin{align*} \displaystyle \int_0^\infty \frac{x^{a-1}} {1+x^n} \,dx=\frac{\pi}{n\sin \frac{a\pi}{n}} .\end{align*} using complex analysis, \(0< a < n\). Here \(n\) is a positive integer.
Fall 2020.3, Spring 2019.2
^5fa654
Let \(a \in \mathbb{R}\) with \(0<a<3\). Evaluate \begin{align*} \int_{0}^{\infty} \frac{x^{a-1}}{1+x^{3}} d x .\end{align*}
Write \(I\) for the integral, \(\zeta_3\coloneqq e^{2\pi i\over 3}, \omega_3 \coloneqq e^{i\pi\pver 3}\). Take a indented semicircular wedge \(\Gamma\) at an angle of \(2\pi/3\), noting the pole at \(\omega_3 \coloneqq e^{i \pi \over 3}\):
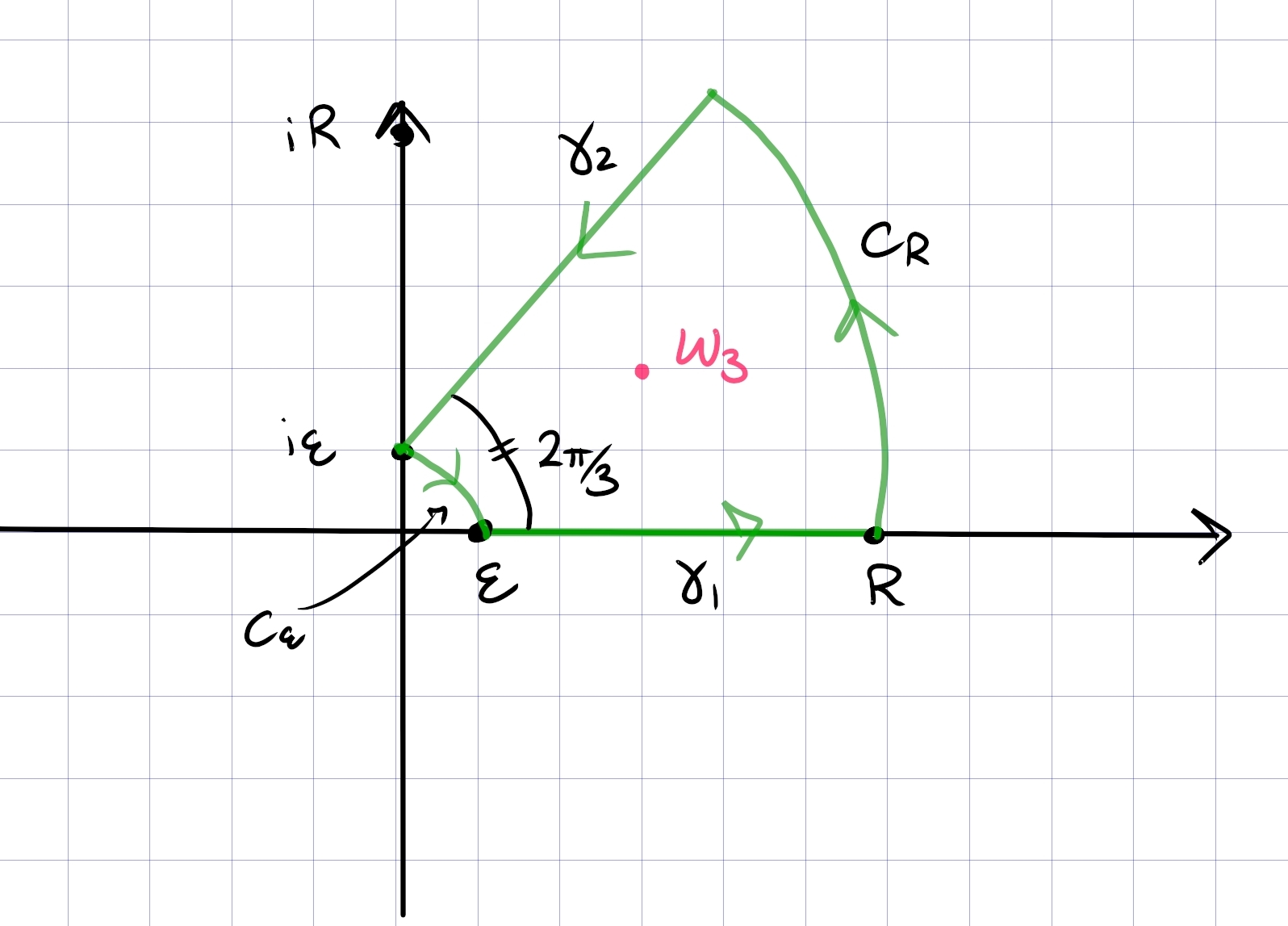
Choosing a branch cut of \(\log\) along \(\theta = -\pi/2\), so \(\arg(z) \in (-\pi/2, 3\pi/2)\), this makes \(f(z) \coloneqq z^{\alpha-1}/(1+z^3)\) meromorphic on \(\Gamma\).
By the ML estimate, the integrals along \(C_{\varepsilon}, C_R\) will vanish in the limit.
The contribution from the contour: parameterize \(\gamma_2\) as \(\left\{{\zeta_3 t{~\mathrel{\Big\vert}~}t\in [{\varepsilon}, R]}\right\}\), then \begin{align*} \int_{\gamma_2}f(z) \,dz &= \int_R^{\varepsilon}{(\zeta_3 t)^{\alpha - 1} \over 1 + (\zeta_3 t)^3} \zeta_3\,dt\\ &= \zeta_3 \zeta_3^{\alpha-1}\int_R^{\varepsilon}{t^{\alpha-1} \over 1 + t^3}\,dt\\ &\to -\zeta_3^\alpha I ,\end{align*} so the total contribution is \begin{align*} \oint_\Gamma f \to \qty{\int_{\gamma_1} + \int_{\gamma_2}}f = (1-\zeta_3^{\alpha}) I .\end{align*}
Computing the contributions from residues: \begin{align*} \mathop{\mathrm{Res}}_{z=\omega_3} f(z) &= \lim_{z\to \omega_3} {(z-\omega_3) z^{\alpha-1} \over 1+z^3} \\ &{ \overset{\scriptscriptstyle\text{LH}}{=} }\lim_{z\to\omega_3} {z^{\alpha-1} \over 3z^2} \\ &= {1\over 3} \omega_3^{\alpha-3} \\ &= -{1\over 3}\omega_3^\alpha .\end{align*}
Combining it all using the residue theorem: \begin{align*} 2\pi i \mathop{\mathrm{Res}}_{z=\omega_3} f(z) &= \oint_\gamma f \\ \implies I &= {-2\pi i\over 3} {\omega_3^\alpha \over 1-\zeta_3^\alpha } \\ &= {-2\pi i\over 3} {1 \over \omega_3^{-\alpha} - \omega_3^\alpha } \\ &= {-2\pi i\over 3} {1 \over -2i\sin\qty{\pi\alpha\over 3} } \\ &= {\pi\over 3}\csc\qty{\alpha\pi\over 3} .\end{align*}
Rational Functions of \(\sin\) or \(\cos\)
Cosine in denominator
Show \begin{align*} \int_0^{2\pi} {1\over a + \cos(\theta)} \,d\theta= {2\pi \over \sqrt{a^2-1}}, && a> 1 .\end{align*}
Sketch:
-
Set \(z=e^{i\theta}\) to get \begin{align*} \frac{2}{i} \int_{|z|=1} \frac{\mathrm{d} z}{z^{2}+2 a z+1} .\end{align*}
-
Factor into two roots \(r_1, r_2\). Use that without loss of generality, \(r_1\in {\mathbb{D}}\) and \(r_2\in {\mathbb{D}}^c\), with neither on \(S^1\) to compute the residue \(4\pi/(r_1 -r_2)\)
Spring 2020 HW 2, SS 2.6.1
Show that \begin{align*} \int_{0}^{\infty} \sin \left(x^{2}\right) d x=\int_{0}^{\infty} \cos \left(x^{2}\right) d x=\frac{\sqrt{2 \pi}}{4} .\end{align*}
Hint: integrate \(e^{-x^2}\) over the following contour, using the fact that \(\int_{-\infty}^{\infty} e^{-x^{2}} d x=\sqrt{\pi}\):
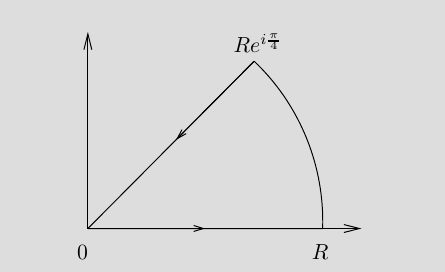 \
\
Spring 2020 HW 3, SS 3.8.8
Show that if \(a,b\in {\mathbb{R}}\) with \(a > {\left\lvert {b} \right\rvert}\), then \begin{align*} \int_{0}^{2 \pi} \frac{d \theta}{a+b \cos \theta}=\frac{2 \pi}{\sqrt{a^{2}-b^{2}}} .\end{align*}
Fresnel
Suppose \(a>b>0\) and calculate \begin{align*} \int_0^{2\pi} {1 \over (a+b\cos(\theta))^2} \,d\theta .\end{align*}
Fresnel
Let \(n\in {\mathbb{Z}}^{\geq 1}\) and \(0<\theta<\pi\) and show that \begin{align*} {1\over 2\pi i} \int_{{\left\lvert {z} \right\rvert} = 2} {z^n \over 1 -3z\cos(\theta) + z^2} \,dz = {\sin(n\theta) \over \sin(\theta)} .\end{align*}
Spring 2020 HW 3.10
For \(a> 0\), evaluate \begin{align*} \int_0^{\pi/2} \frac{d\theta}{a + \sin^2 \theta} \end{align*}
Spring 2020 HW 3, SS 3.8.7
Show that \begin{align*} \int_{0}^{2 \pi} \frac{d \theta}{(a+\cos \theta)^{2}}=\frac{2 \pi a}{\left(a^{2}-1\right)^{3 / 2}}, \quad \text { whenever } a>1 .\end{align*}
Rectangles
Spring 2021.2
^0a6802
Let \(\xi\in {\mathbb{R}}\), evaluate \begin{align*} \int_{\mathbb{R}}{e^{i\xi x} \over \cosh(x)} \,dx .\end{align*}
Note \(\cosh(z) \coloneqq{1\over 2}(e^z + e^{-z})\), and \begin{align*} \cosh(z) &= 0 \\ \iff e^z + e^{-z} &= 0 \\ \iff e^{-z}(e^{2z} + 1) &= 0 \\ \iff e^{2z} &= -1 \quad \text{since }{\left\lvert {e^{-z}} \right\rvert} = e^{\Re(z)} > 0 \\ \iff 2z &= (2k+1)i\pi \\ \iff z &\in \left\{{\cdots, {-3i\pi \over 2}, {-i\pi \over 2}, {i\pi \over 2}, {3i\pi \over 2}, \cdots}\right\} .\end{align*} So take the following rectangular contour enclosing the singularity \(z= i\pi/2\):
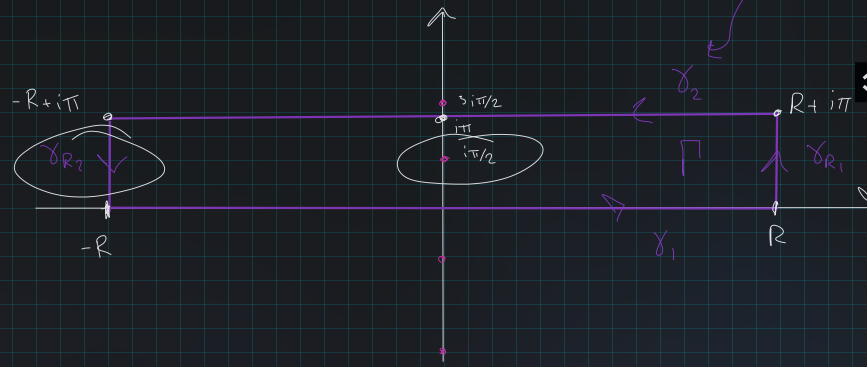
Then letting \(\Gamma\) be the entire contour and \(I\) be the desired integral, we can solve for \(I\): \begin{align*} \int_\Gamma f &= \int_{-R}^R f + \int_{\gamma_{R_1}} f + \int_{\gamma_2}f + \int_{\gamma_{R_2}} f \\ \int_\Gamma f &= I + \int_{\gamma_{R_1}} f + \int_{\gamma_2}f + \int_{\gamma_{R_2}} f \\ \\ I &= \int_{\gamma_{R_1}} f + \int_{\gamma_2}f + \int_{\gamma_{R_2}} f - \int_\Gamma f ,\end{align*} being very sloppy about the fact that we’re going to take \(R\to \infty\).
Computing the residue term \(\int_\Gamma f = 2\pi i \mathop{\mathrm{Res}}_{z=i\pi/2} f(z)\): \begin{align*} {1\over 2\ pi i } \int_\Gamma f &= \mathop{\mathrm{Res}}_{z = i\pi/2} f(z)\\ &= \mathop{\mathrm{Res}}_{z = i\pi/2} {e^{i\xi z} \over \cosh(z) } \\ &= {e^{i\xi z} \over {\frac{\partial }{\partial t}\,} \cosh(z) } \Big|_{i\pi/2}\\ &= {e^{i\xi \cdot i\pi/2} \over \sinh(i\pi/2)} \\ &= {e^{-\xi \pi/ 2} \over i} \\ \implies 2\pi i \mathop{\mathrm{Res}}_{z=i\pi/2} f(z) &= 2\pi e^{-\xi \pi/ 2} .\end{align*} using that \(2\sinh(i\pi/2) = e^{i\pi/2} - e^{-i\pi/2} = i-(-i) = 2i\).
The \(\gamma_2\) term: parameterize \(\gamma_2 = \left\{{t + i\pi {~\mathrel{\Big\vert}~}t\in [-R, R]}\right\}\), then \begin{align*} \int_{\gamma_2} f &= -\int_{-\gamma_2} f \\ &= -\int_{-R}^{R} { e^{iz} \over \cosh(t + i\pi) } \,dz, \quad z = t+i\pi, \,dz= \,dt\\ &= -\int_{-R}^{R} { e^{i\xi(t+i\pi)} \over \cosh(t + i\pi) }\,dt\\ &= -e^{-\xi \pi} \int_{-R}^R {e^{i\xi t} \over \cosh(t+i\pi)} \,dt\\ &= e^{-\xi \pi} \int_{-R}^R {e^{i\xi t} \over \cosh(t)} \,dt\\ &\coloneqq e^{-\xi \pi} I ,\end{align*} using that \(\cosh(z + i\pi) = -\cosh(z)\).
The two \(\gamma_{R_i}\) terms: the claim is that these vanish in the limit \(R\to \infty\). Parameterize \(\gamma_{R_2} = \left\{{R = i \pi t {~\mathrel{\Big\vert}~}t\in [0, 1]}\right\}\), then \begin{align*} {\left\lvert {\int_{\gamma_{R_2}} f} \right\rvert} &= {\left\lvert { \int_0^1 {e^{i\xi(R+i\pi t)} \over \cosh(R + i\pi t)} \,dt} \right\rvert} \\ &= {\left\lvert { 2e^{i\xi R} \int_0^1 {e^{-\xi \pi t } \over {e^{R+ i\pi t} + e^{-R - i\pi t}} } \,dt} \right\rvert} \\ &\leq 2 \int_0^1 {\left\lvert { {e^{-\xi \pi t } \over {e^{R+ i\pi t} + e^{-R - i\pi t}} } } \right\rvert} \,dt\\ &\leq 2 \int_0^1 {e^{-\xi \pi t } \over { {\left\lvert { e^{R+ i\pi t} } \right\rvert} - {\left\lvert { e^{-R - i\pi t} } \right\rvert} } }\,dt\\ &= 2 \int_0^1 {e^{-\xi\pi t} \over e^R - e^{-R} } \\ &= { 2\over e^R - e^{-R}} \int_0^1 e^{-\xi \pi t} \,dt\\ &= {2\over e^R - e^{-R}} \qty{-1\over \xi \pi} e^{\xi \pi t}\Big|_{t=0}^{t=1} \\ &= {2\over e^R - e^{-R}} \qty{1 - e^{-\pi \xi } \over \xi \pi} \\ &\overset{R\to\infty}\longrightarrow 0 .\end{align*}
Putting it all together: \begin{align*} (1 + e^{-\xi \pi}) I &= 2\pi e^{-\xi \pi / 2} \\ \implies I &= {2\pi e^{-\xi \pi / 2} \over 1 + e^{-\xi \pi }} \\ &= {2\pi \over e^{\xi\pi/2} (1 + e^{-\xi \pi })} \\ &= {2\pi \over e^{\xi\pi/2} + e^{-\xi\pi/2} } \\ &= {2\pi \over 2\cosh(\xi\pi/2)} \\ &= {\pi \over \cosh\qty{\xi\pi\over 2}} \\ \\ &= \pi \operatorname{sech}\qty{\xi\pi\over 2 } .\end{align*}
Spring 2020 HW 3, SS 3.8.9
Show that \begin{align*} \int_{0}^{1} \log (\sin \pi x) d x=-\log 2 .\end{align*}
Hint: use the following contour.
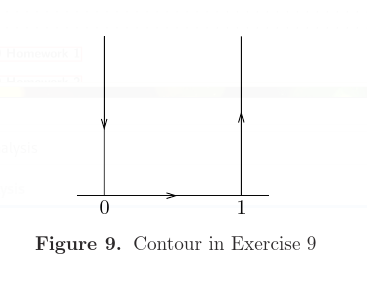
Branch Cuts
Tie’s Extra Questions: Spring 2015
Compute the following integrals:
- \(\displaystyle \int_0^\infty \frac{x^{a-1}}{1 + x^n} \, dx\), \(0< a < n\)
- \(\displaystyle \int_0^\infty \frac{\log x}{(1 + x^2)^2}\, dx\)
Spring 2020 HW 3, SS 3.8.10
Show that if \(a>0\), then \begin{align*} \int_{0}^{\infty} \frac{\log x}{x^{2}+a^{2}} d x=\frac{\pi}{2 a} \log a .\end{align*}
Hint: use the following contour.
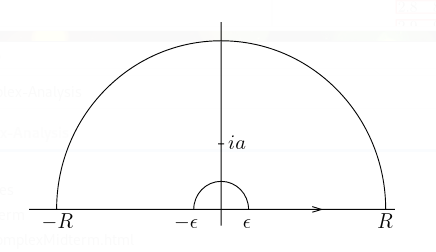
Spring 2020.2
^c765ed
Compute the following integral carefully justifying each step:
\begin{align*} \int_{0}^{\infty} \frac{\log x}{1+x^{3}} \text {. } \end{align*}
Square root in numerator
Calculate \begin{align*} \int_0^\infty {\sqrt x \over (x+1)^2} \,dx .\end{align*}
Square root
Calculate \begin{align*} \int_0^\infty {\sqrt x \over 1 + x^2} \, dx .\end{align*}
Trigonometric transforms
Spring 2020 HW 3, SS 3.8.4
Show that \begin{align*} \int_{-\infty}^{\infty} \frac{x \sin x}{x^{2}+a^{2}} d x=\pi e^{-a}, \quad \text { for all } a>0 .\end{align*}
Spring 2020 HW 2, 2.6.2
Show that
\begin{align*} \int_{0}^{\infty} \frac{\sin x}{x} d x=\frac{\pi}{2} .\end{align*}
Hint: use the fact that this integral eexercises \(\frac{1}{2 i} \int_{-\infty}^{\infty} \frac{e^{i x}-1}{x} d x\), and integrate around an indented semicircle.
Spring 2020 HW 3, SS 3.8.5
Show that if \(\xi\in {\mathbb{R}}\), then \begin{align*} \int_{-\infty}^{\infty} \frac{e^{-2 \pi i x \xi}}{\left(1+x^{2}\right)^{2}} d x=\frac{\pi}{2}(1+2 \pi|\xi|) e^{-2 \pi|\xi|} .\end{align*}
\(\sin\) in numerator
Let \(a>0\) and calculate \begin{align*} \int_0^\infty {x\sin(x) \over x^2 + a^2} \,dx .\end{align*}
\(\sin\) in numerator
Calculate \begin{align*} \int_0^\infty {\sin(x) \over x(x^2+1)}\, dx .\end{align*}
\(\operatorname{sinc}\)
Calculate \begin{align*} \int_0^\infty {\sin(x) \over x}\, dx .\end{align*}
\(\cos\) in numerator
Let \(a>0\) and calculate \begin{align*} \int_0^\infty {\cos(x) \over (x^2 + a^2)^2}\, dx .\end{align*}
\(\sin\) in numerator
Calculate \begin{align*} \int_0^\infty {\sin^3(x) \over x^3} \, dx .\end{align*}
\(\sin\) in numerator
Evaluate \begin{align*} \displaystyle{ \int_{0}^{\infty}\frac{x\sin x}{x^2+a^2} \, dx } .\end{align*}
Tie’s Extra Questions: Fall 2009
Evaluate \begin{align*}\displaystyle{ \int_{0}^{\infty}\frac{x\sin x}{x^2+a^2} \, dx }.\end{align*}
Cosine over quadratic
Show that \begin{align*} \int_0^{\infty} {\cos(x) \over x^2 + b^2}\,dx= {\pi e^{-b} \over 2b} .\end{align*}
-
Let \(I\) be the integral over \({\mathbb{R}}\). Since \(f(x)\) is even, the original integral is \({1\over 2}I\).
-
Write \(f(z) = e^{iz} / (z^2 + b^2)\). Take a semicircular contour \(\Gamma \coloneqq\gamma_1 + \gamma_2\) where \(\gamma_1\) is \([-R, R]\) on \({\mathbb{R}}\) and \(\gamma_2\) is the usual half-circle of radius \(R\).
-
Claim: \(\int_{\gamma_2} f \overset{R\to\infty}\longrightarrow 0\), so \(\int_\Gamma \to \int_{\mathbb{R}}f(z)\).
- Easy estimate, just be careful with the \(i\) in the exponent: \begin{align*} {\left\lvert {f} \right\rvert} = { {\left\lvert {e^{iz} } \right\rvert} \over {\left\lvert {z^2 + b^2} \right\rvert} } = {e^{-\Re z} \over {\left\lvert {z^2 + b^2} \right\rvert} } \leq {1\over {\left\lvert {z^2 + b^2} \right\rvert}} \overset{R\to\infty}\longrightarrow 0 .\end{align*}
-
Compute \(\int_\Gamma f\) by residues: factor \(z^2 + b^2 = (z+ib)(z-ib)\), so the contour only contains the order 1 pole \(z_0 = ib\).
-
Compute the residue: \begin{align*} \mathop{\mathrm{Res}}_{z=ib}f = \lim_{z\to ib} (z-ib) {e^{iz} \over (z+ib)(z-ib) } = { e^{iz} \over z+ib} \Big|_{z=ib} = {e^{i(ib)} \over 2ib} = {e^{-b} \over 2ib} .\end{align*}
-
So the intermediate integral is \(I\) is \(2\pi i\) times this, i.e. \(I = \pi e^{-b} / b\).
-
And the original integral is \({1\over 2}I = \pi e^{-b} \over 2b\).
Tie’s Extra Questions: Fall 2016
Compute the integral \(\displaystyle{\int_{-\infty}^{\infty} \frac{e^{-2\pi ix\xi}}{\cosh\pi x}dx}\) where \(\displaystyle{\cosh z=\frac{e^{z}+e^{-z}}{2}}\).
Tie’s Extra Questions: Fall 2015
Prove by justifying all steps that for all \(\xi \in {\mathbb C}\) we have \(\displaystyle e^{- \pi \xi^2} = \int_{- \infty}^\infty e^{- \pi x^2} e^{2 \pi i x \xi} dx \; .\)
Hint: You may use that fact in Example 1 on p. 42 of the textbook without proof, i.e., you may assume the above is true for real values of \(\xi\).
Multiple cosines in numerator
Calculate \begin{align*} \int_0^\infty {\cos(x) - \cos(4x) \over x^2} \, dx .\end{align*}
Tie’s Extra Questions: Fall 2011
Evaluate \(\displaystyle{ \int_{0}^{\infty}\frac{x\sin x}{x^2+a^2} \,dx}\).
Unsorted
Spring 2020 HW 3.6
-
Show (without using 3.8.9 in the S&S) that \begin{align*} \int_0^{2\pi} \log{\left\lvert {1 - e^{i\theta}} \right\rvert}~d\theta = 0 \end{align*}
-
Show that this identity is equivalent to S&S 3.8.9: \begin{align*} \int_0^1 \log(\sin(\pi x)) ~dx = -\log 2 .\end{align*}
Tie’s Extra Questions: Spring 2015
Compute the following integrals.
-
\(\displaystyle \int_0^\infty \frac{1}{(1 + x^n)^2} \, dx\), \(n \geq 1\)
-
\(\displaystyle \int_0^\infty \frac{\cos x}{(x^2 + a^2)^2} \, dx\), \(a \in \mathbb R\)
-
\(\displaystyle \int_0^\pi \frac{1}{a + \sin \theta} \, d \theta\), \(a>1\)
-
\(\displaystyle \int_0^{\frac{\pi}{2}} \frac{d \theta}{a+ \sin ^2 \theta},\) \(a >0\).
-
\(\displaystyle \int_{|z|=2} \frac{1}{(z^{5} -1) (z-3)} \, dz\)
-
\(\displaystyle \int_{- \infty}^{\infty} \frac{\sin \pi a}{\cosh \pi x + \cos \pi a} e^{- i x \xi} \, d x\), \(0< a <1\), \(\xi \in \mathbb R\)
-
\(\displaystyle \int_{|z| = 1} \cot^2 z \, dz\).
Conceptual
Spring 2020 HW 3, SS 3.8.1
Use the following formula to show that the complex zeros of \(\sin(\pi z)\) are exactly the integers, and they are each of order 1: \begin{align*} \sin \pi z=\frac{e^{i \pi z}-e^{-i \pi z}}{2 i} .\end{align*}
Calculate the residue of \({1\over \sin(\pi z)}\) at \(z=n\in {\mathbb{Z}}\).
Zeros using residue theorem
Suppose that \(f\) is an analytic function in the region \(D\) which contains the point \(a\). Let \begin{align*}F(z)= z-a-qf(z),\quad \text{where}\quad q \ \text{is a complex parameter}.\end{align*}
-
Let \(K\subset D\) be a circle with the center at point \(a\) and also we assume that \(f(z)\not =0\) for \(z\in K\). Prove that the function \(F\) has one and only one zero \(z=w\) on the closed disc \(\mkern 1.5mu\overline{\mkern-1.5muK\mkern-1.5mu}\mkern 1.5mu\) whose boundary is the circle \(K\) if \begin{align*} \displaystyle{ |q|<\min_{z\in K} \frac{|z-a|}{|f(z)|}.} .\end{align*}
-
Let \(G(z)\) be an analytic function on the disk \(\mkern 1.5mu\overline{\mkern-1.5muK\mkern-1.5mu}\mkern 1.5mu\). Apply the residue theorem to prove that \begin{align*} \displaystyle{ \frac{G(w)}{F'(w)}=\frac{1}{2\pi i}\int_K \frac{G(z)}{F(z)} dz,} \end{align*} where \(w\) is the zero from (1).
Tie’s Extra Questions: Fall 2009
Suppose that \(f\) is an analytic function in the region \(D\) which contains the point \(a\). Let \begin{align*}F(z)= z-a-qf(z),\quad \text{where}~ q \ \text{is a complex parameter}.\end{align*}
-
Let \(K\subset D\) be a circle with the center at point \(a\) and also we assume that \(f(z)\not =0\) for \(z\in K\). Prove that the function \(F\) has one and only one zero \(z=w\) on the closed disc \(\mkern 1.5mu\overline{\mkern-1.5muK\mkern-1.5mu}\mkern 1.5mu\) whose boundary is the circle \(K\) if \(\displaystyle{ |q|<\min_{z\in K} \frac{|z-a|}{|f(z)|}.}\)\
-
Let \(G(z)\) be an analytic function on the disk \(\mkern 1.5mu\overline{\mkern-1.5muK\mkern-1.5mu}\mkern 1.5mu\). Apply the residue theorem to prove that \(\displaystyle{ \frac{G(w)}{F'(w)}=\frac{1}{2\pi i}\int_K \frac{G(z)}{F(z)} dz,}\) where \(w\) is the zero from (1).\
-
If \(z\in K\), prove that the function \(\displaystyle{\frac{1}{F(z)}}\) can be represented as a convergent series with respect to \(q\): \(\displaystyle{ \frac{1}{F(z)}=\sum_{n=0}^{\infty} \frac{(qf(z))^n}{(z-a)^{n+1}}.}\)
Tie’s Extra Questions: Spring 2015
Let \(\displaystyle{\psi_{\alpha}(z)=\frac{\alpha-z}{1-\mkern 1.5mu\overline{\mkern-1.5mu\alpha\mkern-1.5mu}\mkern 1.5muz}}\) with \(|\alpha|<1\) and \(\mathbb D = \{z:\ |z|<1\}\). Prove that
-
\begin{align*} \displaystyle{\frac{1}{\pi}\iint_{{\mathbb D}} |\psi'_{\alpha}|^2 dx dy =1} .\end{align*}
-
\begin{align*} \displaystyle{\frac{1}{\pi}\iint_{{\mathbb D}} |\psi'_{\alpha}| dx dy =\frac{1-|\alpha|^2}{|\alpha|^2} \log \frac{1}{1-|\alpha|^2}} .\end{align*}
Part 1: S&S claim this can be done without a calculation – maybe \({\left\lvert {\psi_a'(z)} \right\rvert}^2\) is constant on a circle of radius \(r\)…?
Part 2: \begin{align*} {1\over \pi} \iint_{\mathbb{D}}{\left\lvert {\psi_a'(z)} \right\rvert} \,dz &= {1\over \pi} \iint_{\mathbb{D}}{\left\lvert {1- {\left\lvert {a} \right\rvert}^2 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu z)^2 } \right\rvert} \,dz\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 \int_0^{2\pi} {1 \over {\left\lvert { 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu re^{it} } \right\rvert}^2 } r\,dt\,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 \int_0^{2\pi} {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu re^{it} )(1 - a re^{-it}) } r\,dt\,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 \oint_{{{\partial}}{\mathbb{D}}} {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu rz )(1 - a r \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu) } {r\over iz} \,dz\,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 \oint_{{{\partial}}{\mathbb{D}}} {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu rz )(1 - a r z^{-1}) } {r\over iz} \,dz\,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 {r\over i} \cdot \oint_{{{\partial}}{\mathbb{D}}} {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu rz )(z - a r) } \,dz\,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 {r\over i} \cdot 2\pi i \mathop{\mathrm{Res}}_{z=ar} {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu rz )(z - a r) } \,dr\\ &= {1- {\left\lvert {a} \right\rvert}^2 \over \pi} \int_0^1 {r\over i} \cdot 2\pi i {1 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu rz ) }\Big|_{z=ar} \,dr\\ &= {2\pi \qty{ 1- {\left\lvert {a} \right\rvert}^2} \over \pi} \int_0^1 {r \over 1- {\left\lvert {a} \right\rvert}^2r^2 } \,dr\\ &= {1-{\left\lvert {a} \right\rvert}^2 \over {\left\lvert {a} \right\rvert}^2} \log\qty{1 \over 1 - {\left\lvert {a} \right\rvert}^2 } .\end{align*}
Cauchy’s Theorem
Entire and \(O\) of polynomial implies polynomial
Let \(f(z)\) be entire and assume that \({\left\lvert {f(z)} \right\rvert} \leq M |z|^2\) outside of some disk for some constant \(M\). Show that \(f(z)\) is a polynomial in \(z\) of degree \(\leq 2\).
-
Prove a more general statement: if \({\left\lvert {f(z)} \right\rvert} \leq M{\left\lvert {z} \right\rvert}^n\), then \(f\) is a polynomial of degree at most \(n\).
-
Since \(f\) is entire, it is analytic everywhere, so \(f(z) = \sum_{k\geq 0}c_k z^k\) where \(c_k = f^{(k)}(0)/n!\) is given by the coefficient of its Taylor expansion about \(z=0\).
-
Applying Cauchy’s estimate, on a circle of radius \(R\), \begin{align*} {\left\lvert {f^{(k)}(0)} \right\rvert} \leq { \sup_{\gamma}{\left\lvert {f(z)} \right\rvert} n! \over R^k} \leq {M{\left\lvert {z} \right\rvert}^n n! \over R^k} = {M R^n n! \over R^k} .\end{align*}
-
So for \(k \geq n+1\), this goes to zero as \(R\to \infty\), so \({\left\lvert {f^{k}(0)} \right\rvert} = 0\) for all such \(k\).
-
But then \(f\) is a power series annihilated by taking \(n+1\) derivatives, so it is a polynomial of degree at most \(n\).
Uniform sequence implies uniform derivatives
Let \(a_n(z)\) be an analytic sequence in a domain \(D\) such that \(\displaystyle \sum_{n=0}^\infty |a_n(z)|\) converges uniformly on bounded and closed sub-regions of \(D\). Show that \(\displaystyle \sum_{n=0}^\infty |a'_n(z)|\) converges uniformly on bounded and closed sub-regions of \(D\).
Tie’s Extra Questions: Spring 2014
The question provides some insight into Cauchy’s theorem. Solve the problem without using the Cauchy theorem.
-
Evaluate the integral \(\displaystyle{\int_{\gamma} z^n dz}\) for all integers \(n\). Here \(\gamma\) is any circle centered at the origin with the positive (counterclockwise) orientation.
-
Same question as (a), but with \(\gamma\) any circle not containing the origin.
-
Show that if \(|a|<r<|b|\), then \(\displaystyle{\int_{\gamma}\frac{dz}{(z-a)(z-b)} dz=\frac{2\pi i}{a-b}}\). Here \(\gamma\) denotes the circle centered at the origin, of radius \(r\), with the positive orientation.
\begin{align*} \int_\gamma z^n\,dz= \int_0^{2\pi} R^n e^{itn} \cdot iRe^{it} \,dt = R^{n+1} \int_0^{2\pi} e^{i(t+1)n}\,dt = { i R^{n+1} \over i(n+1) } \delta_{n+1 = 0} .\end{align*}
About a point \(a\) and \(R<{\left\lvert {a} \right\rvert}\), \begin{align*} \int_{{\left\lvert {z-a} \right\rvert} = R} z^n\,dz &= \int_0^{2\pi} (a + re^{it})^n \cdot ire^{it}\,dt\\ &= \int_0^{2\pi} \sum_{1\leq k\leq n} {n \choose k} a_k R^{n-k+1} e^{it(n-k)} \cdot ire^{it}\,dt\\ &= i \int_0^{2\pi} \sum_{1\leq k\leq n} {n \choose k} a_k R^{n-k+1} e^{it(n-k+1)} \,dt\\ &= i \sum_{1\leq k\leq n} {n \choose k} a_k R^{n-k+1} \int_0^{2\pi} e^{it(n-k+1)} \,dt\\ &= i \sum_{1\leq k\leq n} {n \choose k} a_k R^{n-k+1} \cdot 0 \\ &= 0 ,\end{align*} provided \(n\neq 0\), in which case \(\int_\gamma \,dz= 2\pi\).
For the third computation, this follows from partial fraction decomposition.
Fall 2019.3, Spring 2020 HW 2.9 (Cauchy’s Formula for Exterior Regions)
^f2a684
Let \(\gamma\) be a piecewise smooth simple closed curve with interior \(\Omega_1\) and exterior \(\Omega_2\). Assume \(f'\) exists in an open set containing \(\gamma\) and \(\Omega_2\) with \(\lim_{z\to \infty} f(z) = A\). Show that \begin{align*} F(z) \coloneqq\frac{1}{2 \pi i} \int_{\gamma} \frac{f(\xi)}{\xi-z} d \xi=\left\{\begin{array}{ll} A, & \text { if } z \in \Omega_{1} \\ -f(z)+A, & \text { if } z \in \Omega_{2} \end{array}\right. .\end{align*}
NOTE (DZG): I think there is a typo in this question….probably this should equal \(f(z)\) for \(z\in \Omega_1\), which is Cauchy’s formula…
Note that \(G_z(\xi) \coloneqq{f(\xi) \over \xi - z}\) has a pole of order one at \(\xi = z\) and also a pole at \(\xi = \infty\). If \(z\in \Omega_1\), then \(\gamma\) encloses just the pole \(\xi = z\), so apply the residue theorem: \begin{align*} F(z) &\coloneqq{1\over 2\pi i}\oint_\gamma {f(\xi) \over \xi - z}\,d\xi\\ &= {1\over 2\pi i}\oint_\gamma G_z(\xi) \,d\xi\\ &= \mathop{\mathrm{Res}}_{\xi = z} G_z(\xi) \\ &= \lim_{\xi\to z} (\xi - z) G_z(\xi) \\ &= \lim_{\xi\to z} (\xi - z) {f(\xi) \over \xi-z} \\ &= \lim_{\xi\to z} f(\xi) \\ &= f(z) .\end{align*}
Now if \(z\in \Omega_2\), then \(\gamma\) encloses both \(\xi=z, \infty\), and is oriented negatively,so \begin{align*} F(z) &= {1\over 2\pi i} \oint_\gamma G_z(\xi) \,d\xi\\ &= -\qty{\mathop{\mathrm{Res}}_{\xi = z} G_z(\xi) + \mathop{\mathrm{Res}}_{\xi = \infty} G_z(\xi)}\\ &= -\qty{f(z) + \mathop{\mathrm{Res}}_{\xi = \infty} G_z(\xi)}\\ ,\end{align*} where the last line proceeds by the same calculation as above. It remains to compute the unknown residue. Residues at \(\xi = \infty\) are computed as residues at \(\xi =0\), and the change of variables \(G_z(\xi)\,d\xi\mapsto G_z(w) \,dw\) for \(w\coloneqq 1/\xi\) yields \(G_z(\xi)\,d\xi\to G_z\qty{1\over \xi}(-1/\xi^2)\,d\xi\). Thus \begin{align*} \mathop{\mathrm{Res}}_{\xi=\infty} G_z(\xi) &= -\mathop{\mathrm{Res}}_{\xi=0} G_z\qty{\xi^{-1}}\xi^{-2} \\ &= - \mathop{\mathrm{Res}}_{\xi=0} {f(\xi^{-1}) \over \xi^2(\xi^{-1}- z) } \\ &= - \mathop{\mathrm{Res}}_{\xi=0} {f(\xi^{-1}) \over \xi(1 - z\xi) } \\ &= -\lim_{\xi \to 0} {f(\xi^{-1}) \over 1-z\xi} \\ &= -\lim_{\xi \to 0}f(\xi ^{-1}) \\ &= -\lim_{\xi\to\infty} f(\xi) \\ &= -A .\end{align*} So combining this yields \begin{align*} F(z) = -\qty{f(z) - A} = -f(z) + A .\end{align*}
Tie’s Extra Questions: Fall 2009 (Proving Cauchy using Green’s)
State and prove Green’s Theorem for rectangles. Use this to prove Cauchy’s Theorem for functions that are analytic in a rectangle.
Suppose \(f\in C_{\mathbb{C}}^1(\Omega)\) and \(T\subset \Omega\) is a triangle with \(T^\circ \subset \Omega\).
- Apply Green’s theorem to show that \(\int_T f(z) ~dz = 0\).
- Assume that \(f'\) is continuous and prove Goursat’s theorem.
Hint: Green’s theorem states \begin{align*} \int_{T} F d x+G d y=\int_{T^\circ}\left(\frac{\partial G}{\partial x}-\frac{\partial F}{\partial y}\right) d x d y .\end{align*}
Green’s theorem: if \(\Omega\) is a domain with positively oriented boundary with \(u, v\) continuously differentiable in \(\mkern 1.5mu\overline{\mkern-1.5mu\Omega\mkern-1.5mu}\mkern 1.5mu\), then \begin{align*} \int_{{{\partial}}\Omega} u\,dx+ v\,dy= \iint_{\Omega}\qty{v_x - u_y}\,dx\,dy .\end{align*} Now use that if \(f = u+iv\) is analytic in a region, it satisfies Cauchy-Riemann: \begin{align*} u_x = v_y \qquad u_y = -v_x .\end{align*}
Now integrating \(f\): \begin{align*} \oint_{{{\partial}}\Omega} f(z) \,dz &= \oint_{{{\partial}}\Omega} (u+iv)(\,dx+ i\,dy)\\ &= \oint_{{{\partial}}\Omega} \qty{u\,dx- v\,dy} + i\oint_{{{\partial}}\Omega} \qty{v\,dx+ u\,dy} \\ &= \iint_\Omega\qty{v_x + u_y}\,dx\,dy+ \iint_\Omega\qty{u_x - v_y}\,dx\,dy\\ &= \iint_\Omega\qty{v_x -v_x }\,dx\,dy+ \iint_\Omega\qty{u_x - u_x}\,dx\,dy\\ &= 0 .\end{align*}
No polynomials converging uniformly to \(1/z\)
Prove that there is no sequence of polynomials that uniformly converge to \(f(z) = {1\over z}\) on \(S^1\).
- By Cauchy’s integral formula, \(\int_{S^1} f = 2\pi i\)
- If \(p_j\) is any polynomial, then \(p_j\) is holomorphic in \({\mathbb{D}}\), so \(\int_{S^1} p_j = 0\).
- Contradiction: compact sets in \({\mathbb{C}}\) are bounded, so \begin{align*} {\left\lvert {\int f - \int p_j} \right\rvert} &\leq \int {\left\lvert {p_j - f} \right\rvert} \\ &\leq \int {\left\lVert {p_j - f} \right\rVert}_\infty \\ &= {\left\lVert {p_j - f} \right\rVert}_\infty \int_{S^1} 1 \,dz \\ &= {\left\lVert {p_j-f} \right\rVert}_\infty \cdot 2\pi \\ &\to 0 \end{align*} which forces \(\int f = \int p_j = 0\).
Eventually sublinear implies constant
Suppose \(f: {\mathbb{C}}\to {\mathbb{C}}\) is entire and \begin{align*} {\left\lvert {f(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}^{1\over 2} \quad\text{ when } {\left\lvert {z} \right\rvert} > 10 .\end{align*}
Prove that \(f\) is constant.
Let \(R> 10\), then by Cauchy: \begin{align*} 2\pi {\left\lvert {f'(z)} \right\rvert} &\leq \oint_{{\left\lvert {\xi} \right\rvert} = R} { {\left\lvert { f(\xi)} \right\rvert} \over {\left\lvert {\xi} \right\rvert}^2 } \,d\xi\\ &\leq \oint_{{\left\lvert {\xi} \right\rvert} = R} R^{-2} {\left\lvert {\xi} \right\rvert}^{1\over 2} \,d\xi\\ &= R^{-{3\over 2}} \cdot 2\pi R \\ &\sim R^{-{1\over 2}} \\ &\overset{R\to\infty}\longrightarrow 0 .\end{align*}
The Cauchy pole function is holomorphic
Let \(\gamma\) be a smooth curve joining two distinct points \(a, b\in {\mathbb{C}}\).
Prove that the function \begin{align*} f(z) \coloneqq\int_\gamma {g(w) \over w-z} \,dw \end{align*} is analytic in \({\mathbb{C}}\setminus\gamma\).
Toward applying Morera, let \(T \subseteq {\mathbb{C}}\setminus\gamma\) be a triangle, so that \(z\in T\) and \(w\in \gamma\) implies \(z-w\neq 0\). Then \begin{align*} \oint_T f(z) \,dz &= \oint_T \int_\gamma {g(w)\over w-z}\,dw\,dz\\ &= \int_\gamma \oint_T {g(w)\over w-z}\,dz\,dw\\ &= \int_\gamma g(w) \qty{ \oint_T {1 \over w-z}\,dz} \,dw\\ &= \int_\gamma g(w) \cdot 0 \,dw\\ &= 0 ,\end{align*} where the exchange of integrals is justified by compactness of \(\gamma, T\), and the inner integral vanishes because for a fixed \(w\in \gamma\), the function \(z\mapsto {1\over w-z}\) has a simple pole at \(w\), and so is holomorphic in \(\gamma^c\) and vanishes by Goursat.
Schwarz reflection proof
Suppose that \(f: {\mathbb{C}}\to{\mathbb{C}}\) is continuous everywhere and analytic on \({\mathbb{C}}\setminus {\mathbb{R}}\) and prove that \(f\) is entire.
Just reproducing the proof of holomorphicity in the Schwarz reflection theorem.
- Note \(f\) is continuous on \({\mathbb{C}}\) since analytic implies continuous (\(f\) equals its power series, where the partials sums uniformly converge to it, and uniform limit of continuous is continuous).
- Strategy: take \(D\) a disc centered at a point \(x\in {\mathbb{R}}\), show \(f\) is holomorphic in \(D\) by Morera’s theorem.
- Let \(\Delta \subset D\) be a triangle in \(D\).
- Case 1: If \(\Delta \cap{\mathbb{R}}= 0\), then \(f\) is holomorphic on \(\Delta\) and \(\int_\Delta f = 0\).
-
Case 2: one side or vertex of \(\Delta\) intersects \({\mathbb{R}}\), and wlog the rest of \(\Delta\) is in \({\mathbb{H}}^+\).
- Then let \(\Delta_{\varepsilon}\) be the perturbation \(\Delta + i{\varepsilon}= \left\{{z+ i{\varepsilon}{~\mathrel{\Big\vert}~}z\in \Delta}\right\}\); then \(\Delta_{\varepsilon}\cap{\mathbb{R}}= 0\) and \(\int_{\Delta_{\varepsilon}} f = 0\).
-
Now let \({\varepsilon}\to 0\) and conclude by continuity of \(f\) (???)
-
We want
\begin{align*} \int_{\Delta_{\varepsilon}} f = \int_a^b f(\gamma_{\varepsilon}(t)) \gamma_{\varepsilon}'(t)\,dt \overset{{\varepsilon}\to 0}\to \int_a^b f(\gamma(t)) \gamma_{\varepsilon}'(t)\,dt =\int_{\Delta} f \end{align*}where \(\gamma_{\varepsilon}, \gamma\) are curves parametrizing \(\Delta_{\varepsilon}, \Delta\) respectively. - Since \(\gamma, \gamma_{\varepsilon}\) are closed and bounded in \({\mathbb{C}}\), they are compact subsets. Thus it suffices to show that \(f(\gamma_{\varepsilon}(t)) \gamma_{\varepsilon}'(t)\) converges uniformly to \(f(\gamma(t))\gamma'(t)\).
- ??
-
We want
-
Case 3: \(\Delta\) intersects both \({\mathbb{H}}^+\) and \({\mathbb{H}}^-\).
- Break into smaller triangles, each of which falls into one of the previous two cases.
Prove Liouville
Prove Liouville’s theorem: suppose \(f:{\mathbb{C}}\to{\mathbb{C}}\) is entire and bounded. Use Cauchy’s formula to prove that \(f'\equiv 0\) and hence \(f\) is constant.
The main idea: \begin{align*} {\left\lvert {f'(z)} \right\rvert} &\leq {1\over 2\pi }\oint_R {{\left\lvert {f(\xi)} \right\rvert} \over {\left\lvert {\xi} \right\rvert}^2 } \,d\xi\\ &= {1\over 2\pi }\oint_R {{\left\lvert {f(\xi)} \right\rvert} } R^{-2} \,d\xi\\ &\leq {1\over 2\pi }\oint_R M R^{-2} \,d\xi\\ &= {1\over 2\pi} MR^{-2}\cdot 2\pi R \\ &= MR^{-1} \\ &\overset{R\to\infty}\longrightarrow 0 .\end{align*} So \(f'\equiv 0\).
Tie’s Extra Questions Fall 2009 (Fractional residue formula)
Assume \(f\) is continuous in the region: \begin{align*} 0 < {\left\lvert {z-a} \right\rvert} \leq R,\quad 0 \leq \operatorname{Arg}(z-a) \leq \beta_0 \qquad \beta_0\in (0, 2\pi] .\end{align*}
and the following limit exists: \begin{align*} \lim_{z\to a}(z-a)f(z) = A .\end{align*} Show that \begin{align*}\lim_{r \rightarrow 0} \int_{\gamma_r} f(z) dz = i A \beta_0 \; , \; \;\end{align*} where \begin{align*} \gamma_r : = \{ z \; | \; z = a + r e^{it}, \; 0 \leq t \leq \beta_0 \}. .\end{align*}
Let \(f\) be a continuous function in the region \begin{align*} D=\{z {~\mathrel{\Big\vert}~}{\left\lvert {z} \right\rvert}>R, 0\leq \arg z\leq \theta\}\quad\text{where}\quad 1\leq \theta \leq 2\pi .\end{align*} If there exists \(k\) such that \(\displaystyle{\lim_{z\to\infty} zf(z)=k}\) for \(z\) in the region \(D\). Show that \begin{align*} \lim_{R'\to\infty} \int_{L} f(z) dz=i\theta k ,\end{align*} where \(L\) is the part of the circle \(|z|=R'\) which lies in the region \(D\).
Without loss of generality take \(a=0\). Since \(zf(z) \to A\) as \(z\to 0\), \(z=0\) is a simple pole of \(f\) and we can write \(f(z) = c_{-1}z^{-1}+ c_0 + c_1z + \cdots\). Then \begin{align*} \int_{\gamma_r} f(z)\,dz &= \int_{\gamma_r} \sum_{k\geq -1} c_k z^k \,dz\\ &= \sum_{k\geq -1} c_k \int_{\gamma_r} z^k \,dz\\ &= c_{-1}\int_{\gamma_r}{1\over z}\,dz\\ &= c_{-1}\int_{0}^{\beta_0} {1\over re^{i t}} ire^{it} \,dt\qquad z= re^{it}, \,dz= ire^{it} \,dt\\ &= i c_{-1}\int_{0}^{\beta_0} \,dt\\ &= i c_{-1}\beta_0 .\end{align*} Now use that \begin{align*} zf(z) = c_{-1} + c_0z + \cdots \overset{z\to 0}\longrightarrow c_{-1} = A ,\end{align*} so the integral is \(iA\beta_0\).
Spring 2020 HW 2, 2.6.7
Suppose \(f: {\mathbb{D}}\to {\mathbb{C}}\) is holomorphic and let \(d \coloneqq\sup_{z, w\in {\mathbb{D}}}{\left\lvert {f(z) - f(w)} \right\rvert}\) be the diameter of the image of \(f\). Show that \(2 {\left\lvert {f'(0)} \right\rvert} \leq d\), and that equality holds iff \(f\) is linear, so \(f(z) = a_1 z + a_2\).
Hint: \begin{align*} 2f'(0) = \frac{1}{2\pi i} \int_{{\left\lvert {\xi } \right\rvert}= r} \frac{ f(\xi) - f(-\xi) }{\xi^2} ~d\xi \end{align*} whenever \(0<r<1\).
Spring 2020 HW 2, 2.6.8
Suppose that \(f\) is holomorphic on the strip \(S = \left\{{x+iy {~\mathrel{\Big\vert}~}x\in {\mathbb{R}},~ -1<y<1}\right\}\) with \({\left\lvert {f(z)} \right\rvert} \leq A \qty{1 + {\left\lvert {z} \right\rvert}}^\nu\) for \(\nu\) some fixed real number. Show that for all \(z\in S\), for each integer \(n\geq 0\) there exists an \(A_n \geq 0\) such that \({\left\lvert {f^{(n)}(x)} \right\rvert} \leq A_n (1 + {\left\lvert {x} \right\rvert})^\nu\) for all \(x\in {\mathbb{R}}\).
Hint: Use the Cauchy inequalities.
Spring 2020 HW 2, 2.6.9
Let \(\Omega \subset {\mathbb{C}}\) be open and bounded and \(\phi: \Omega \to \Omega\) holomorphic. Prove that if there exists a point \(z_0 \in \Omega\) such that \(\phi(z_0) = z_0\) and \(\phi'(z_0) = 1\), then \(\phi\) is linear.
Hint: assume \(z_0 = 0\) (explain why this can be done) and write \(\phi(z) = z + a_n z^n + O(z^{n+1})\) near \(0\). Let \(\phi_k = \phi \circ \phi \circ \cdots \circ \phi\) and prove that \(\phi_k(z) = z + ka_nz^n + O(z^{n+1})\). Apply Cauchy’s inequalities and let \(k\to \infty\) to conclude.
Spring 2020 HW 2, 6
Show by example that there exists a function \(f(z)\) that is holomorphic on \(\left\{{z\in {\mathbb{C}}{~\mathrel{\Big\vert}~}0 < {\left\lvert {z} \right\rvert} < 1}\right\}\) and for all \(r<1\), \begin{align*} \int_{{\left\lvert {z} \right\rvert} = r} f(z) \, dz = 0 ,\end{align*} but \(f\) is not holomorphic at \(z=0\).
Spring 2020 HW 2, 7
Let \(f\) be analytic on a region \(R\) and suppose \(f'(z_0) \neq 0\) for some \(z_0 \in R\). Show that if \(C\) is a circle of sufficiently small radius centered at \(z_0\), then \begin{align*} \frac{2 \pi i}{f^{\prime}\left(z_{0}\right)}=\int_{C} \frac{d z}{f(z)-f\left(z_{0}\right)} .\end{align*}
Hint: use the inverse function theorem.
Spring 2020 HW 2, 8
Assume two functions \(u, b: {\mathbb{R}}^2 \to {\mathbb{R}}\) have continuous partial derivatives at \((x_0 ,y_0)\). Show that \(f \coloneqq u + iv\) has derivative \(f'(z_0)\) at \(z_0 = x_0 + iy_0\) if and only if \begin{align*} \lim _{r \rightarrow 0} \frac{1}{\pi r^{2}} \int_{\left|z-z_{0}\right|=r} f(z) d z=0 .\end{align*}
Spring 2020 HW 2, 10
Let \(f(z)\) be bounded and analytic in \({\mathbb{C}}\). Let \(a\neq b\) be any fixed complex numbers. Show that the following limit exists: \begin{align*} \lim_{R\to \infty} \int_{{\left\lvert {z} \right\rvert} = R} {f(z) \over (z-a)(z-b)} \,dz .\end{align*}
Use this to show that \(f(z)\) must be constant.
Spring 2020 HW 2, 11
Suppose \(f(z)\) is entire and \begin{align*} \lim_{z\to\infty} {f(z) \over z} = 0 .\end{align*}
Show that \(f(z)\) is a constant.
Spring 2020 HW 2, 12
Let \(f\) be analytic in a domain \(D\) and \(\gamma\) be a closed curve in \(D\). For any \(z_0\in D\) not on \(\gamma\), show that \begin{align*} \int_{\gamma} \frac{f^{\prime}(z)}{\left(z-z_{0}\right)} d z=\int_{\gamma} \frac{f(z)}{\left(z-z_{0}\right)^{2}} d z .\end{align*} Give a generalization of this result.
Spring 2020 HW 2, 13
Compute \begin{align*} \int_{{\left\lvert {z} \right\rvert} = 1} \qty{z + {1\over z}}^{2n} {dz \over z} \end{align*} and use it to show that \begin{align*} \int_0^{2\pi} \cos^{2n}(\theta) \, d\theta = 2\pi \qty{1\cdot 3 \cdot 5 \cdots (2n-1) \over 2 \cdot 4 \cdot 6 \cdots (2n)} .\end{align*}
Maximum Modulus
Spring 2020 HW 3.8
Prove the fundamental theorem of Algebra using the maximum modulus principle.
Spring 2020.7
^aff739
Let \(f\) be analytic on a bounded domain \(D\), and assume also that \(f\) that is continuous and nowhere zero on the closure \(\mkern 1.5mu\overline{\mkern-1.5muD\mkern-1.5mu}\mkern 1.5mu\).
Show that if \(|f(z)|=M\) (a constant) for \(z\) on the boundary of \(D\), then \(f(z)=e^{i \theta} M\) for \(z\) in \(D\), where \(\theta\) is a real constant.
By the maximum modulus principle, \({\left\lvert {f} \right\rvert} \leq M\) in \(\mkern 1.5mu\overline{\mkern-1.5muD\mkern-1.5mu}\mkern 1.5mu\). Since \(f\) has no zeros in \(\mkern 1.5mu\overline{\mkern-1.5muD\mkern-1.5mu}\mkern 1.5mu\), \(g\coloneqq 1/f\) is holomorphic on \(D\) and continuous on \(\mkern 1.5mu\overline{\mkern-1.5muD\mkern-1.5mu}\mkern 1.5mu\). So the maximum modulus principle applies to \(g\), and \(M^{-1}\geq {\left\lvert {g} \right\rvert} = 1/{\left\lvert {f} \right\rvert}\), so \({\left\lvert {f} \right\rvert} \leq M\). Combining these, \({\left\lvert {f(z)} \right\rvert} = M\), so \(f(z) = \lambda M\) where \(\lambda\) is some constant with \({\left\lvert {\lambda} \right\rvert}=1\). This is on the unit circle, so \(\lambda = e^{i\theta}\) for some fixed angle \(\theta\).
Fall 2020.6
^189826
Suppose that \(U\) is a bounded, open and simply connected domain in \(\mathbb{C}\) and that \(f(z)\) is a complex-valued non-constant continuous function on \(\mkern 1.5mu\overline{\mkern-1.5muU\mkern-1.5mu}\mkern 1.5mu\) whose restriction to \(U\) is holomorphic.
- Prove the maximum modulus principle by showing that if \(z_{0} \in U\), then
\begin{align*} \left|f\left(z_{0}\right)\right|<\sup \{|f(z)|: z \in \partial U\} . \end{align*}
- Show furthermore that if \(|f(z)|\) is constant on \(\partial U\), then \(f(z)\) has a zero in \(U\) (i.e., there exists \(z_{0} \in U\) for which \(f\left(z_{0}\right)=0\) ).
Let \(M\coloneqq\sup_{z\in {{\partial}}U}{\left\lvert {f(z)} \right\rvert}\). If \(M=0\), then \(f\) must be the constant zero function, so assume \(M>0\).
Suppose toward a contradiction that there exists a \(z_0 \in U\) with \({\left\lvert {f(z_0)} \right\rvert} = M\). Note that the map \(z\mapsto {\left\lvert {z} \right\rvert}\) is an open in discs that don’t intersect \(z=0\). Since \(f\) is holomorphic, by the open mapping theorem \(f\) is an open map, so consider \(D_{\varepsilon}(z_0)\) a small disk not containing \(0\). Then \(f(D_{\varepsilon}(z_0))\) is open, and the composition \(z\mapsto f(z) \mapsto {\left\lvert {f(z)} \right\rvert}\) is an open map \(D_{\varepsilon}(z_0)\to {\mathbb{R}}\). Now if \(f\) is nonconstant, \({\left\lvert {f(D_{\varepsilon}(z_0))} \right\rvert} \supseteq(M-{\varepsilon}, M+{\varepsilon})\) contains some open interval about \(M\), which contradicts maximality of \(f\) at \(z_0\).
See notes for a proof using the mean value theorem.
Suppose toward a contradiction that \(f\) has no zeros in \(U\). Then \(g(z) \coloneqq 1/f(z)\) is holomorphic in \(U\). Now if \({\left\lvert {f(z)} \right\rvert} = C\) on \({{\partial}}U\), we have \({\left\lvert {g(z)} \right\rvert} = {\left\lvert {1\over f(z)} \right\rvert} = {1\over C}\) on \({{\partial}}U\), so \(\max_{z\in U} {\left\lvert {f(z)} \right\rvert} = C\) and \(\min_{{\left\lvert {f(z)} \right\rvert}} = {1\over C}\). Since \({\left\lvert {f(z)} \right\rvert}\) is constant on the boundary, we must have \(\max {\left\lvert {f(z)} \right\rvert} = \min {\left\lvert {f(z)} \right\rvert} = C\), so \(f\) is constant on \({{\partial}}U\). By the identity principle, \(f\) is constant on \(U\), a contradiction.
Spring 2020 HW 3, SS 3.8.15
Use the Cauchy inequalities or the maximum modulus principle to solve the following problems:
-
Prove that if \(f\) is an entire function that satisfies \begin{align*} \sup _{|z|=R}|f(z)| \leq A R^{k}+B \end{align*} for all \(R>0\), some integer \(k\geq 0\), and some constants \(A, B > 0\), then \(f\) is a polynomial of degree \(\leq k\).
-
Show that if \(f\) is holomorphic in the unit disc, is bounded, and converges uniformly to zero in the sector \(\theta < \arg(z) < \phi\) as \({\left\lvert {z} \right\rvert} \to 1\), then \(f \equiv 0\).
-
Let \(w_1, \cdots w_n\) be points on \(S^1 \subset {\mathbb{C}}\). Prove that there exists a point \(z\in S^1\) such that the product of the distances from \(z\) to the points \(w_j\) is at least 1. Conclude that there exists a point \(w\in S^1\) such that the product of the above distances is exactly 1.
-
Show that if the real part of an entire function is bounded, then \(f\) is constant.
\begin{align*} {\left\lvert { f(z_0) } \right\rvert} &= {\left\lvert { {1\over 2\pi i} \oint_{{\left\lvert {z-z_0} \right\rvert} = R } {f(z) \over (z-z_0)^{n+1} } \,dz} \right\rvert} \\ &\leq {1\over 2\pi } \oint_{{\left\lvert {z-z_0} \right\rvert} = R } {\left\lvert {f(z)} \right\rvert} R^{-(n+1)} \,dz\\ &\leq {1\over 2\pi }\sup_{{\left\lvert {z-z_0} \right\rvert} = R} {\left\lvert {f(z)} \right\rvert} R^{-(n+1)} \cdot 2\pi R \\ &= \sup_{{\left\lvert {z-z_0} \right\rvert} = R} {\left\lvert {f(z)} \right\rvert} R^{-n} \\ &\leq (AR^k + B)R^{-n} \qquad \text{ if } z_0 = 0 \\ &= AR^{k-n} + BR^{-n} \\ &\to 0 ,\end{align*} provided \(k-n< 0\), so \(n>k\). Since \(f\) is entire, write \begin{align*} f(z) = \sum_{n\geq 0} f^{(n)}(0) {z^n\over n!} = \sum_{0\leq n\leq k} f^{(n)}(0) {z^n\over n!} ,\end{align*} making \(f\) a polynomial of degree at most \(k\).
Write \(S_\phi \coloneqq\left\{{0<\operatorname{Arg}(z) < \phi}\right\}\) and choose \(n\) large enough so that \begin{align*} {\mathbb{D}}\subseteq S \cup\zeta_n S \cup\zeta_n^2 S \cup\cdots\cup\zeta_{n}^{n-1}S ,\end{align*} i.e. so that the rotated sectors cover the disc. By uniform convergence of \(f\) to \(0\) on \(S\), choose \(r<1\) small enough so that \({\left\lvert {f(z)} \right\rvert} < {\varepsilon}\) for \({\left\lvert {z} \right\rvert} < r\) in \(S\). Note that \({\mathbb{D}}_r \subseteq \displaystyle\bigcup_{k=0}^{n-1} \zeta_n^k S_r\), where \(S_r \coloneqq\left\{{z\in S {~\mathrel{\Big\vert}~}{\left\lvert {z} \right\rvert} \leq r}\right\}\) is a subsector of radius \(r\).
By the MMP, let \(M\) be the maximum of \(f\) on \({\mathbb{D}}\), which is attained at some point on \(S^1\). Then \({\left\lvert {f} \right\rvert} < M\) on every \(\zeta_n^k S_r\). Now define \begin{align*} g(z) \coloneqq f(z) \prod_{k=1}^{n-1} f(\zeta_n^k z) \coloneqq f(z) \prod_{k=1}^{n-1}f_k(z) .\end{align*} Note that \({\left\lvert {f(z)} \right\rvert}\leq {\varepsilon}\) and \({\left\lvert {f_k(z)} \right\rvert} \leq M\), so \begin{align*} {\left\lvert {g(z)} \right\rvert}\leq {\varepsilon}\cdot M^{n-1} \overset{{\varepsilon}\to 0}\longrightarrow 0 .\end{align*} since \(M\) is a constant. So \(g(z) \equiv 0\) on \({\mathbb{D}}_r\), and by the identity principle, on \({\mathbb{D}}\). Thus some factor \(f_k(z)\) is identically zero. But if \(f(\zeta_n^k z)\equiv 0\) on \({\mathbb{D}}\), then \(f(z) \equiv 0\) on \({\mathbb{D}}\), since every \(z\in {\mathbb{D}}\) can be written as \(\zeta_n^k w\) for some \(w\in {\mathbb{D}}\).
Consider \begin{align*} f(z) \coloneqq\prod_{1\leq k \leq n} (w_k - z) .\end{align*} Then \(f\) is holomorphic and nonconstant on \({\mathbb{D}}\), so attains a maximum \(M\) on \(S^1\). Moreover, \({\left\lvert {f(z)} \right\rvert} = \prod {\left\lvert {w_k-z} \right\rvert}\) is exactly the product of distances from \(z\) to the \(w_k\). Moreover, since \({\left\lvert {f(0)} \right\rvert} = \prod{\left\lvert {w_k} \right\rvert} = 1\), we must have \(M>1\).
Now note that \(f(w_k) = 0\) and \(f\) is continuous in \({\mathbb{D}}\). So \({\left\lvert {f(z)} \right\rvert} \in [0, M] \subseteq {\mathbb{R}}\) where \(M>1\), so by the intermediate value theorem, \({\left\lvert {f(z)} \right\rvert} = 1\) for some \(z\).
Write \(f=u+iv\) where by assumption \(u\) is bounded. Both \(u\) and \(v\) are harmonic, so if \({\left\lvert {u} \right\rvert} \leq M\) on \({\mathbb{C}}\), then there is some disc where \({\left\lvert {u} \right\rvert} = M\) for some point in the interior. By the MMP for harmonic functions, \(u\) is constant on \({\mathbb{C}}\). So \(u_x, u_y = 0\), and by Cauchy-Riemann, \(v_x, v_y = 0\), so \(v'=0\) and \(v\) is constant, making \(f\) constant.
Consider \(g(z) \coloneqq e^{f(z)}\), then \({\left\lvert {g(z)} \right\rvert} = e^{\Re(z)}\) is entire and bounded and thus constant by Liouville’s theorem. So \(g'(z) = 0\), but on the other hand \(g'(z) = f'(z) e^{f(z)} = 0\), so \(f'(z) = 0\) and \(f\) must be constant since \(e^f\) is nonvanishing.
Spring 2020 HW 3, 3.8.17
Let \(f\) be non-constant and holomorphic in an open set containing the closed unit disc.
- Show that if \({\left\lvert {f(z)} \right\rvert} = 1\) whenever \({\left\lvert {z} \right\rvert} = 1\), then the image of \(f\) contains the unit disc.
Hint: Show that \(f(z) = w_0\) has a root for every \(w_0 \in {\mathbb{D}}\), for which it suffices to show that \(f(z) = 0\) has a root. Conclude using the maximum modulus principle.
- If \({\left\lvert {f(z)} \right\rvert} \geq 1\) whenever \({\left\lvert {z} \right\rvert} = 1\) and there exists a \(z_0\in {\mathbb{D}}\) such that \({\left\lvert {f(z_0)} \right\rvert} < 1\), then the image of \(f\) contains the unit disc.
Spring 2020 HW 3, 3.8.19
Prove that maximum principle for harmonic functions, i.e.
-
If \(u\) is a non-constant real-valued harmonic function in a region \(\Omega\), then \(u\) can not attain a maximum or a minimum in \(\Omega\).
-
Suppose \(\Omega\) is a region with compact closure \(\mkern 1.5mu\overline{\mkern-1.5mu\Omega\mkern-1.5mu}\mkern 1.5mu\). If \(u\) is harmonic in \(\Omega\) and continuous in \(\mkern 1.5mu\overline{\mkern-1.5mu\Omega\mkern-1.5mu}\mkern 1.5mu\), then \begin{align*} \sup _{z \in \Omega}|u(z)| \leq \sup _{z \in \mkern 1.5mu\overline{\mkern-1.5mu\Omega \mkern-1.5mu}\mkern 1.5mu-\Omega}|u(z)| .\end{align*}
Hint: to prove (a), assume \(u\) attains a local maximum at \(z_0\). Let \(f\) be holomorphic near \(z_0\) with \(\Re(f) = u\), and show that \(f\) is not an open map. Then (a) implies (b).
Spring 2020 HW 3.9
Let \(f\) be analytic in a region \(D\) and \(\gamma\) a rectifiable curve in \(D\) with interior in \(D\).
Prove that if \(f(z)\) is real for all \(z\in \gamma\), then \(f\) is constant.
Spring 2020 HW 3.14
Let \(f\) be nonzero, analytic on a bounded region \(\Omega\) and continuous on its closure \(\overline \Omega\).
Show that if \({\left\lvert {f(z)} \right\rvert} \equiv M\) is constant for \(z\in \partial \Omega\), then \(f(z) \equiv Me^{i\theta}\) for some real constant \(\theta\).
Tie’s Extra Questions: Spring 2015
Let \(\displaystyle{\psi_{\alpha}(z)=\frac{\alpha-z}{1-\mkern 1.5mu\overline{\mkern-1.5mu\alpha\mkern-1.5mu}\mkern 1.5muz}}\) with \(|\alpha|<1\) and \({\mathbb D}=\{z:\ |z|<1\}\). Prove that
-
\(\displaystyle{\frac{1}{\pi}\iint_{{\mathbb D}} |\psi'_{\alpha}|^2 dx dy =1}\).
-
\(\displaystyle{\frac{1}{\pi}\iint_{{\mathbb D}} |\psi'_{\alpha}| dx dy =\frac{1-|\alpha|^2}{|\alpha|^2} \log \frac{1}{1-|\alpha|^2}}\).
Tie’s Extra Questions: Spring 2015
Let \(\Omega\) be a simply connected open set and let \(\gamma\) be a simple closed contour in \(\Omega\) and enclosing a bounded region \(U\) anticlockwise. Let \(f: \ \Omega \to {\mathbb C}\) be a holomorphic function and \(|f(z)|\leq M\) for all \(z\in \gamma\). Prove that \(|f(z)|\leq M\) for all \(z\in U\).
Tie’s Extra Questions: Fall 2015
Assume \(f(z)\) is analytic in region \(D\) and \(\Gamma\) is a rectifiable curve in \(D\) with interior in \(D\). Prove that if \(f(z)\) is real for all \(z \in \Gamma\), then \(f(z)\) is a constant.
Liouville’s Theorem
Spring 2020.3, Extras Fall 2009
^c6e205
- Assume \(f(z)=\sum_{n=0}^{\infty} c_{n} z^{n}\) converges in \(|z|<R\). Show that for \(r<R\),
\begin{align*} \frac{1}{2 \pi} \int_{0}^{2 \pi}\left|f\left(r e^{i \theta}\right)\right|^{2} d \theta=\sum_{n=0}^{\infty}\left|c_{n}\right|^{2} r^{2 n} \end{align*}
- Deduce Liouville’s theorem from (a).
Computing the LHS: \begin{align*} \int_{[0, 2\pi]} {\left\lvert {f(re^{i\theta})} \right\rvert}^2 \,d\theta &= \int_{[0, 2\pi]} f(re^{i\theta}) \mkern 1.5mu\overline{\mkern-1.5muf(re^{i\theta}) \mkern-1.5mu}\mkern 1.5mu \,d\theta\\ &= \int_{[0, 2\pi]} \sum_{k\geq 0} c_k r^k e^{ik\theta} \sum_{j\geq 0} \mkern 1.5mu\overline{\mkern-1.5muc_j\mkern-1.5mu}\mkern 1.5mu r^j e^{-ij\theta} \,d\theta\\ &= \int_{[0, 2\pi]} \sum_{k,j\geq 0} c_k\mkern 1.5mu\overline{\mkern-1.5muc_j\mkern-1.5mu}\mkern 1.5mu r^{k+j} e^{i(k-j)\theta} \,d\theta\\ &= \sum_{k,j\geq 0} c_k\mkern 1.5mu\overline{\mkern-1.5muc_j\mkern-1.5mu}\mkern 1.5mu r^{k+j} \int_{[0, 2\pi]} e^{i(k-j)\theta} \,d\theta\\ &= \sum_{k,j\geq 0} c_k\mkern 1.5mu\overline{\mkern-1.5muc_j\mkern-1.5mu}\mkern 1.5mu r^{k+j} \chi_{i=j}\cdot 2\pi \\ &= \sum_{k\geq 0} c_k\mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu r^{2k} \cdot 2\pi \\ &= 2\pi \sum_{k\geq 0}{\left\lvert {c_k} \right\rvert}^2 r^{2k} ,\end{align*} where we’ve used that the series converges uniformly in its radius of convergence to commute sums and integrals.
Now supposing \({\left\lvert {f(z)} \right\rvert}\leq M\) for all \(z\in {\mathbb{C}}\), if \(f\) is entire then \(\sum_{k\geq 0} c_k z^k\) converges for all \(r\), so \begin{align*} \sum_{k\geq 0} {\left\lvert {c_k} \right\rvert}^2 r^{2k} = {1\over 2\pi }\int_{[0, 2\pi]} {\left\lvert {f(re^{i\theta})} \right\rvert}^2 \,d\theta\leq {1\over 2\pi}\int_{[0, 2\pi]} M^2 \,d\theta= M^2 .\end{align*} Thus for all \(r\), \begin{align*} {\left\lvert {c_0} \right\rvert}^2 + {\left\lvert {c_1} \right\rvert}^2 r^2 + {\left\lvert {c_2} \right\rvert}^2 r^{4} + \cdots \leq M^2 ,\end{align*} and taking \(r\to\infty\) forces \({\left\lvert {c_1} \right\rvert}^2 = {\left\lvert {c_2} \right\rvert}^2 = \cdots = 0\). So \(f(z) = c_0\) is constant.
FTA via Liouville
Prove the Fundamental Theorem of Algebra (using complex analysis).
- Strategy: By contradiction with Liouville’s Theorem
- Suppose \(p\) is non-constant and has no roots.
-
Claim: \(1/p(z)\) is a bounded holomorphic function on \({\mathbb{C}}\).
-
Holomorphic: clear? Since \(p\) has no roots.
-
Bounded: for \(z\neq 0\), write
\begin{align*} \frac{P(z)}{z^{n}}=a_{n}+\left(\frac{a_{n-1}}{z}+\cdots+\frac{a_{0}}{z^{n}}\right) .\end{align*} -
The term in parentheses goes to 0 as \({\left\lvert {z} \right\rvert}\to \infty\)
-
Thus there exists an \(R>0\) such that
\begin{align*} {\left\lvert {z} \right\rvert} > R \implies {\left\lvert {P(z) \over z^n} \right\rvert} \geq c \coloneqq{{\left\lvert {a_n} \right\rvert} \over 2} .\end{align*} -
So \(p\) is bounded below when \({\left\lvert {z} \right\rvert} > R\)
-
Since \(p\) is continuous and has no roots in \({\left\lvert {z} \right\rvert} \leq R\), it is bounded below when \({\left\lvert {z} \right\rvert} \leq R\).
-
Thus \(p\) is bounded below on \({\mathbb{C}}\) and thus \(1/p\) is bounded above on \({\mathbb{C}}\).
-
- By Liouville’s theorem, \(1/p\) is constant and thus \(p\) is constant, a contradiction.
Entire functions satisfying an inequality
Find all entire functions that satisfy \begin{align*} {\left\lvert {f(z)} \right\rvert} \geq {\left\lvert {z} \right\rvert} \quad \forall z\in {\mathbb{C}} .\end{align*} Prove this list is complete.
- If \(f\) is bounded in a neighborhood of a singularity \(z_0\), then \(z_0\) is removable.
- Suppose \(f\) is entire and define \(g(z) \coloneqq{z \over f(z)}\).
- By the inequality, \({\left\lvert {g(z)} \right\rvert} \leq 1\), so \(g\) is bounded.
- \(g\) potentially has singularities at the zeros \(Z_f \coloneqq f^{-1}(0)\), but since \(f\) is entire, \(g\) is holomorphic on \({\mathbb{C}}\setminus Z_f\).
-
Claim: \(Z_f = \left\{{0}\right\}\).
- If \(f(z) = 0\), then \({\left\lvert {z} \right\rvert} \leq {\left\lvert {f(z)} \right\rvert} = 0\) which forces \(z=0\).
-
We can now apply Riemann’s removable singularity theorem:
- Check \(g\) is bounded on some open subset \(D\setminus\left\{{0}\right\}\), clear since it’s bounded everywhere
- Check \(g\) is holomorphic on \(D\setminus\left\{{0}\right\}\), clear since the only singularity of \(g\) is \(z=0\).
- By Riemann’s removable singularity theorem, the singularity \(z = 0\) is removable and \(g\) has an extension to an entire function \(\tilde g\).
-
By continuity, we have \({\left\lvert {\tilde g(z)} \right\rvert} \leq 1\) on all of \({\mathbb{C}}\)
- If not, then \({\left\lvert {\tilde g(0)} \right\rvert} = 1+{\varepsilon}> 1\), but then there would be a domain \(\Omega \subseteq {\mathbb{C}}\setminus\left\{{0}\right\}\) such that \(1 < {\left\lvert {\tilde g(z)} \right\rvert} \leq 1 +{\varepsilon}\) on \(\Omega\), a contradiction.
- By Liouville, \(\tilde g\) is constant, so \(\tilde g(z) = c_0\) with \({\left\lvert {c_0} \right\rvert} \leq 1\)
- Thus \(f(z) = c_0^{-1}z \coloneqq cz\) where \({\left\lvert {c} \right\rvert}\geq 1\)
Thus all such functions are of the form \(f(z) = cz\) for some \(c\in {\mathbb{C}}\) with \({\left\lvert {c} \right\rvert}\geq 1\).
Entire functions with an asymptotic bound
Find all entire functions satisfying \begin{align*} {\left\lvert {f(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}^{1\over 2} \quad\text{ for } {\left\lvert {z} \right\rvert} > 10 .\end{align*}
Since \(f\) is entire, take a Laurent expansion at \(z=0\), so \(f(z) = \sum_{k\geq 0} c_k z^k\) where \({2\pi i\over k!} c_k = f^{(k)}(0)\) by Cauchy’s integral formula. Take a Cauchy estimate on a disc of radius \(R>10\): \begin{align*} {\left\lvert {c_k} \right\rvert} &\leq {k!\over 2\pi}\int_{{\left\lvert {z} \right\rvert} = R} {\left\lvert {f(\xi) \over (\xi - 0)^{k+1}} \right\rvert}\,d\xi\\ &\leq {k! \over 2\pi}\int_{{\left\lvert {z} \right\rvert} = R}{ {\left\lvert {\xi} \right\rvert}^{1\over 2} \over {\left\lvert {\xi} \right\rvert}^{k+1} }\,d\xi\\ &= {k! \over 2\pi} \cdot {1\over R^{k+{1\over 2}}}\cdot 2\pi R \\ &= { \mathsf{O}} (1/R^{k-{1\over 2}}) .\end{align*} So in particular, if \(k\geq 1\) then \(k-{1\over 2}>0\) and \(c_k = 0\). This forces \(f = c_0\) to be constant.
Tie’s Extra Questions: Fall 2009
Let \(f(z)\) be entire and assume values of \(f(z)\) lie outside a bounded open set \(\Omega\). Show without using Picard’s theorems that \(f(z)\) is a constant.
We have \({\left\lvert {f(z)} \right\rvert}\geq M\) for some \(M\), so \({\left\lvert {1/f(z)} \right\rvert} \leq M^{-1}\) is bounded, and we claim it is entire as well. This follows from the fact that \(1/f\) has singularities at the zeros of \(f\), but these are removable since \(1/f\) is bounded in every neighborhood of each such zero. So \(1/f\) extends to a holomorphic function. But now \(1/f =c\) is constant by Liouville, which forces \(f= 1/c\) to be constant.
Tie’s Extra Questions: Fall 2015
Let \(f(z)\) be bounded and analytic in \(\mathbb C\). Let \(a \neq b\) be any fixed complex numbers. Show that the following limit exists: \begin{align*} \lim_{R \rightarrow \infty} \int_{|z|=R} \frac{f(z)}{(z-a)(z-b)} dz .\end{align*}
Use this to show that \(f(z)\) must be a constant (Liouville’s theorem).
Apply PFD and use that \(f\) is holomorphic to apply Cauchy’s formula over a curve of radius \(R\) enclosing \(a\) and \(b\): \begin{align*} \int_\gamma {f(z) \over (z-a)(z-b)}\,dz &= \int_\gamma f(z)\qty{{a-b \over z-a} + {b-a\over z-b} } \,dz\\ &= (a-b)^{-1}\int_\gamma {f(z) \over z-a} \,dz+ (b-a)^{-1}\int_\gamma {f(z) \over z-b}\,dz\\ &= (a-b)^{-1}\cdot 2\pi i f(a) + (b-a)\cdot 2\pi i f(b)\\ &= 2\pi i\qty{f(a) - f(b) \over a-b } .\end{align*} Since \(f\) is bounded, this number is finite and independent of \(R\), so taking \(R\to\infty\) preserves this equality. On the other hand, if \({\left\lvert {f(z)} \right\rvert}\leq M\), then we can estimate this integral directly as \begin{align*} I \leq \int_{{\left\lvert {z} \right\rvert} = R} {M \over {\left\lvert {R-a} \right\rvert} \cdot {\left\lvert {R-b} \right\rvert} } = {M\cdot 2\pi R \over {\left\lvert {R-a} \right\rvert} \cdot {\left\lvert {R-b} \right\rvert}} \ll {1\over R} \to 0 ,\end{align*} which forces \(f(a) =f(b)\). Since \(a, b\) were arbitrary, \(f\) must be constant.
Polynomials
Big O Estimates
Tie’s Extra Questions: Fall 2011, Fall 2009 (Polynomial upper bound, \(d=2\))
Let \(f(z)\) be entire and assume that \(f(z) \leq M |z|^2\) outside some disk for some constant \(M\). Show that \(f(z)\) is a polynomial in \(z\) of degree \(\leq 2\).
Take a Laurent expansion at zero: \begin{align*} f(z) = \sum_{k\geq 0} c_k z^k,\qquad c_k = {1\over k!} f^{(k)}(0) = {1\over 2\pi i}\oint_{{\left\lvert {\xi} \right\rvert} = R} {f(\xi) \over \xi^{k+1}}\,d\xi .\end{align*} The usual estimate: \begin{align*} 2\pi i{\left\lvert {c_k} \right\rvert} \leq \oint_{{\left\lvert {\xi} \right\rvert} = R} R^{-(k+1)}{\left\lvert {f(\xi)} \right\rvert} \,d\xi &\leq \oint_{{\left\lvert {\xi} \right\rvert} = R}R^{-(k+1)} M R^2 \,d\xi\\ &= M R^{-(k-1)} \cdot 2\pi R \\ &= 2\pi M R^{-k+2} \\ &\overset{R\to\infty}\longrightarrow 0 ,\end{align*} provided \(-k+2<0 \iff k>2\).
Tie’s Extra Questions: Spring 2015, Fall 2016 (Polynomial upper bound, \(d\) arbitrary)
-
Let Let \(f:{\mathbb C}\rightarrow {\mathbb C}\) be an entire function. Assume the existence of a non-negative integer \(m\), and of positive constants \(L\) and \(R\), such that for all \(z\) with \(|z|>R\) the inequality \begin{align*}|f(z)| \leq L |z|^m\end{align*} holds. Prove that \(f\) is a polynomial of degree \(\leq m\).
-
Let \(f:{\mathbb C}\rightarrow {\mathbb C}\) be an entire function. Suppose that there exists a real number \(M\) such that for all \(z\in {\mathbb C}, \Re(f) \leq M\). Prove that \(f\) must be a constant.
\begin{align*} {\left\lvert {f^{(n)}(z)} \right\rvert} &= {\left\lvert { {1\over 2\pi i} \oint_\gamma {f(\xi) \over (\xi - z)^{n+1}} \,d\xi} \right\rvert} \\ &\leq {1\over 2\pi i} \oint_\gamma { {\left\lvert { f(\xi) } \right\rvert} \over {\left\lvert {\xi - z} \right\rvert}^{n+1}} \,d\xi\\ &\leq {1\over 2\pi i } \oint_\gamma {LR^m \over R^{n+1} } \,d\xi\\ &= {L\over 2\pi i} R^{m-(n+1)} \cdot 2\pi R \\ &= LR^{m-n} \\ &\overset{R\to\infty}\longrightarrow 0 \qquad \iff m-n<0 \iff n>m ,\end{align*} so \(f\) is a polynomial of degree at most \(m\).
Now if \(f\) is entire, \(g(z) \coloneqq e^{f(z)}\) is entire and \begin{align*} {\left\lvert {g(z)} \right\rvert} = {\left\lvert {e^{f(z)}} \right\rvert} = e^{\Re(f)} \leq e^M ,\end{align*} so \(g\) is an entire bounded function and thus constant by Liouville, making \(f\) constant. Why this is true: \begin{align*} e^{f} = C \implies e^f \cdor f' = 0 \implies f'\equiv 0 ,\end{align*} since \(e^f\) is nonvanishing, and \(f'\equiv 0\) implies \(f\) is constant.
Asymptotic to \(z^n\)
Suppose \(f\) is entire and suppose that for some integer \(n\geq 1\), \begin{align*} \lim_{z\to \infty} {f(z) \over z^n} = 0 .\end{align*}
Prove that \(f\) is a polynomial of degree at most \(n-1\).
Choose \({\left\lvert {z} \right\rvert}\) large enough so that \({\left\lvert {f(z)} \right\rvert}/{\left\lvert {z} \right\rvert}^n < {\varepsilon}\). Then write \(f(z) = \sum_{k\geq 0} c_k z^k\) and estimate \begin{align*} 2\pi {\left\lvert {c_k} \right\rvert} &\leq \oint_{{\left\lvert {z} \right\rvert} = R} {f(\xi) \over \xi^{k+1}}\,d\xi\\ &\leq \oint_{{\left\lvert {z} \right\rvert} = R} {{\varepsilon}{\left\lvert {\xi} \right\rvert}^n \over {\left\lvert {\xi} \right\rvert}^{k+1} } \,d\xi\\ &= {\varepsilon}R^{n-(k+1)} \cdot 2\pi R \\ &= {\varepsilon}C R^{n-k} \\ &\overset{{\varepsilon}\to 0}\longrightarrow 0 \end{align*} provided \(n-k \leq 0 \iff k\geq n\), since \({\varepsilon}\to 0\) forces \(R\to \infty\).
Spring 2021.3, Tie’s Extra Questions: Spring 2014, Fall 2009 (Polynomial lower bound, \(d\) arbitrary)
^409461
Suppose \(f\) is entire and there exist \(A, R >0\) and natural number \(N\) such that \begin{align*} |f(z)| \geq A |z|^N\ \text{for}\ |z| \geq R .\end{align*}
Show that
- \(f\) is a polynomial and
- the degree of \(f\) is at least \(N\).
The easier version of this question: when \({\left\lvert {f} \right\rvert} \leq A{\left\lvert {z} \right\rvert}^N\), \(f\) is a polynomial of degree at most \(N\) by Cauchy’s integral formula: \begin{align*} {\left\lvert {f^{(n)}(z)} \right\rvert} &= {\left\lvert { {1\over 2\pi i} \oint_\gamma {f(\xi) \over (\xi - z)^{n+1}} \,d\xi} \right\rvert} \\ &\leq {1\over 2\pi i} \oint_\gamma { {\left\lvert { f(\xi) } \right\rvert} \over {\left\lvert {\xi - z} \right\rvert}^{n+1}} \,d\xi\\ &\leq {1\over 2\pi i } \oint_\gamma {AR^N \over R^{n+1} } \,d\xi\\ &= {A\over 2\pi i} R^{N-(n+1)} \cdot 2\pi R \\ &= AR^{N-n} \\ &\overset{R\to\infty}\longrightarrow 0 \qquad \iff N-n<0 \iff n>N .\end{align*}
Now rearrange the given equality \begin{align*} {\left\lvert {f(z) \over z^N} \right\rvert} \geq A \qquad {\left\lvert {z} \right\rvert} \implies {\left\lvert {z^N\over f(z)} \right\rvert} \leq A^{-1} .\end{align*} A priori, \(f\) is equal to its power series at \(z=0\), so \(f(z) = \sum_{k\geq 0} c_k z^k\). Since \({\mathbb{D}}_R\) is compact, \(f\) has finitely many zeros in this region, say \(\left\{{z_k}\right\}_{k\leq m}\). This set must be finite, since an infinite subset of a compact set has a limit point, and being zero on a set with a limit point implies being identically zero by the identity principle.
Define \begin{align*} p(z) \coloneqq\prod_{1\leq k\leq m} (z-z_k) = z^m + { \mathsf{O}} (z^{m-1}) ,\end{align*} the product of these roots. Increase \(R\) if necessary to ensure that \begin{align*} {\left\lvert {p(z)\over z^m} \right\rvert} < 1 \implies {\left\lvert {p(z)} \right\rvert} < {\left\lvert {z} \right\rvert}^m .\end{align*} Now define \begin{align*} G(z) \coloneqq{p(z) z^N \over f(z)} \implies {\left\lvert {G(z)} \right\rvert} = {\left\lvert {p(z) z^N\over f(z)} \right\rvert} = {\left\lvert {z^N\over f(z)} \right\rvert}\cdot {\left\lvert {p(z)} \right\rvert} \leq A^{-1}{\left\lvert {z} \right\rvert}^m .\end{align*}
Issue: this might not be entire? There could be poles at the zeros of \(f\) outside of \({\mathbb{D}}_R\)…
By the previous result, \(G\) is a polynomial of degree at most \(m\). Now consider leading terms: on one hand, \begin{align*} f(z) G(z) = p(z) z^N \sim \qty{z^m + \cdots }\cdot z^N = z^{N+m} + \cdots .\end{align*} On the other hand, \begin{align*} f(z) G(z) &= f(z) \qty{z^m + \cdots} \\ &\sim \sum_{k\geq 0} c_k z^{k+m} + z^{m-1}f(z) + \cdots \\ &= (z^m + \cdots + c_{N}z^{N+m} + \cdots) + z^{m-1}f(z) + \cdots ,\end{align*} and by the previous expression, this must be a polynomial of degree at most \(N+m\). This forces \(c_k = 0\) for all \(k> N\), otherwise these would contribute higher order terms.
Note: maybe not quite right!
Alternatively, note that the inequality can be rewritten as \begin{align*} {\left\lvert {G(z)} \right\rvert} \leq A^{-1}{\left\lvert {z} \right\rvert}^m \implies {\left\lvert {p(z)\over f(z)} \right\rvert} \leq A^{-1}{\left\lvert {z} \right\rvert}^{m-N} .\end{align*}
- If \(m-N = 0\), then \(p/f\) is an entire bounded function and thus constant, making \(p(z) = \lambda f(z)\) and \(f\) is a polynomial of degree exactly \(N\). -If \(m-N>0\), then \(p/f\) is a polynomial of degree at most \(m-N\) by the previous result. But \(p/f\) is a polynomial with no zeros, since \(Z_p = Z_f\), and the only nonvanishing polynomial is a constant, so again \(p = \lambda f\).
- If \(m-N<0\), then use the inequality \begin{align*} {\left\lvert {z^{N-m}p(z) \over f(z)} \right\rvert} \leq A^{-1} ,\end{align*} so the LHS is an entire bounded function and thus constant, so \(z^{N-m}p(z) = \lambda f(z)\). But the LHS is evidently a polynomial of degree \((N-m)+m = m\).
Note that the analogue of this problem where \({\left\lvert {f(z)} \right\rvert} \leq A {\left\lvert {z} \right\rvert}^N\) implies \(f\) is a polynomial of degree at most \(N\) is easy by the Cauchy estimate: \begin{align*} {\left\lvert {f(z)} \right\rvert} ={\left\lvert {\sum_{k\geq 0} c_k z^k } \right\rvert} \implies {\left\lvert {c_n} \right\rvert} = {\left\lvert {f^{(n)}(0)} \right\rvert} &= {\left\lvert {{n!\over 2\pi i }\int_\gamma {f(\xi) \over (\xi-a)^{n+1} } \,d\xi} \right\rvert} \quad \text{ at } a=0\\ &\leq {n!\over 2\pi }\int_\gamma {{\left\lvert {f(\xi)} \right\rvert} \over {\left\lvert {\xi} \right\rvert}^{n+1} } \,d\xi\\ &\leq {n!\over 2\pi }\int_\gamma {A {{\left\lvert {\xi} \right\rvert}^N } \over {\left\lvert {\xi} \right\rvert}^{n+1} } \,d\xi\\ &= {A n!\over 2\pi }\int_\gamma {{R ^N } \over R^{n+1} } \,d\xi\\ &= {An!\over 2\pi} \cdot {2\pi R \over R^{n+1-N}} \\ &= {An! \over R^{n-N}} \\ &\overset{R\to\infty}\longrightarrow 0 \quad \iff n-N>0 \quad\iff n>N ,\end{align*} so \(f(z) = \sum_{0\leq k\leq N} c_k z^k\).
For the case at hand, a solution I liked from MSE:
-
Write \(g(z) \coloneqq f(1/z)\), so \(g\) has a singularity at \(z=0\). The claim is that this is a pole.
-
It can’t be removable: \begin{align*} {\left\lvert {g(z)} \right\rvert} \geq A {\left\lvert {1\over z} \right\rvert}^n \to\infty \quad \text{ for } {\left\lvert {1/z} \right\rvert} \geq R \,\, (\iff {\left\lvert {z} \right\rvert} < 1/R) ,\end{align*} so \(g\) is unbounded near \(z=0\).
-
It can’t be essential: if so, take the neighborhood of \(z=0\) given by \(U\coloneqq D_{1\over R}(0)\setminus\left\{{0}\right\}= \left\{{z{~\mathrel{\Big\vert}~}0< {\left\lvert {z} \right\rvert} < {1\over R} }\right\}\). Then \(g(U) \subseteq {\mathbb{C}}\) would be dense by Casorati-Weierstrass, but note that \(g(z) = w\in g(U) \implies {\left\lvert {w} \right\rvert} \coloneqq{\left\lvert {g(z)} \right\rvert} \geq A{\left\lvert {1/z} \right\rvert}^n\) since \({\left\lvert {z} \right\rvert}<1/R\), so \(g(U) \subseteq ({\mathbb{C}}\setminus D_{A\over R^n}(0))\) and in particular does not intersect the interior of \(D_{A\over R^n}(0)\).
-
Since \(z=0\) is a pole, it has some finite order \(m\), so write \begin{align*} g(z) = \qty{c_{-m}z^{-m} + \cdots + c_{-1}z^{-1}} + \qty{c_0 + c_1 z + \cdots} \coloneqq p(1/z) + h(z) ,\end{align*} where \(p\) is polynomial of degree exactly \(m\) (since \(c_{-m} \neq 0\)) and \(h\) is entire. In particular, \(z=0\) is not a singularity of \(h\).
-
Now \begin{align*} g(z) = p(1/z) + h(z) \implies f(z) = p(z) + h(1/z) .\end{align*}
-
Then \begin{align*} f(z) - p(z) = h(1/z) \overset{{\left\lvert {z} \right\rvert}\to \infty}\longrightarrow c_0 \coloneqq h(0) ,\end{align*} since holomorphic functions are continuous.
-
Then \(h\) is an entire function with a finite limit \(L\) at \(\infty\). \(h\) is bounded by \(c_0\) in a neighborhood \(U_\infty\) of \(\infty\) and takes on a maximum on \(U_\infty^c\) by compactness and the maximum modulus principle. So \(h\) is bounded on all of \({\mathbb{C}}\), and thus constant by Liouville, and thus \(h(1/z) = L\) for all \(z\).
-
So \begin{align*} f(z) &= p(z) + h(1/z) = p(z) + c_0 \\ \implies f(z) &= (c_{-1}z + \cdots + c_{-m}z^m) + c_0 ,\end{align*} which is a polynomial of degree exactly \(m\coloneqq\deg p\).
-
Why \(m \geq N\): if not, \(m<N\) so \(N-m > 0\). Then for large \(z\), \begin{align*} A \leq {\left\lvert {f(z) \over z^N} \right\rvert} &= {\left\lvert {c_0 + c_{-1}z + \cdots + c_{-m}z^m \over z^N} \right\rvert}\\ &= {\left\lvert { {c_0 \over z^N} + {c_{-1} \over z^{N-1}} + \cdots + {c_{-m} \over z^{N-m}} } \right\rvert} \\ &\overset{{\left\lvert {z} \right\rvert}\to\infty}\longrightarrow 0 ,\end{align*} since every term has a factor of \(z\) in the denominator. This contradicts \(A>0\). \(\contradiction\)
Misc
Spring 2021.4
^c3336f
Let \(f = u + iv\) be an entire function such that \(\Re(f(x+iy))\) is polynomial in \(x\) and \(y\). Show that \(f(z)\) is polynomial in \(z\).
To clear up notation: write \(f(z) = u(x, y) + iv(x, y)\), here we’re assuming that \(u\) is polynomial in \(x\) and \(y\).
If \(u\) is polynomial in \(x,y\), then so is \(v\).
This follows from the fact that \(u\) is a harmonic conjugate of \(v\), and the explicit process computing the conjugate will result in a polynomial. Gamelin describes this process in detail, see Ch.2 Section 5 on Harmonic functions where he proves the formula \begin{align*} v(x, y) = \int_{y_{0}}^{y} \frac{\partial u}{\partial x}(x, t) \,dt -\int_{x_{0}}^{x} \frac{\partial u}{\partial y}\left(s, y_{0}\right) \,ds+ C .\end{align*}
Since \(f(x, y)\) is a polynomial in \(x, y\), \(f(z)\) must be a polynomial in \(z\).
Since \(f\) is entire, it’s equal to its Laurent series everywhere, so \begin{align*} f(z) = \sum_{k\geq 0} c_k z^k, \qquad c_k = {f^{(k) }(0) \over k!} = {1\over 2\pi i} \int_{S^1} {f(\xi) \over \xi^{k+1} } \,d\xi .\end{align*} Thus \(f\) will be a polynomial if \(c_{N} = 0\) for all \(N\) large enough, which will be true if \(f^{(N)}(z) = 0\) for large enough \(N\). But we can write \begin{align*} {\frac{\partial }{\partial z}\,} f(z) = {\frac{\partial }{\partial x}\,} f(x, y) \implies 0 = \qty{{\frac{\partial ^N}{\partial x^N}\,}} f(x, y) = \qty{{\frac{\partial ^N}{\partial z^N}\,}} f(z) \coloneqq f^{(N)}(z) ,\end{align*}
Spring 2019.4 (Eventually bounded implies rational)
^047423
Let \(f\) be a meromorphic function on the complex plane with the property that \(|f(z)| \leq\) \(M\) for all \(|z|>R\), for some constants \(M>0, R>0\).
Prove that \(f(z)\) is a rational function, i.e., there exist polynomials \(p, q\) so that \(f=\frac{p}{q}\).
Note that \(f\) must have finitely many poles – either \(z=\infty\) is a pole or a removable singularity, and since poles are isolated, there is some \(R\gg 0\) such that all other poles of \(f\) are in \({\left\lvert {z} \right\rvert} \leq R\). The set \(P_f\) of poles is a closed set and \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}_R\mkern-1.5mu}\mkern 1.5mu\) is compact, so if \(P_f\) is infinite it has an accumulation point, contradicting that poles are isolated.
So enumerate \(P_f\) as \(\left\{{p_k}\right\}_{k\leq N}\), define \(g(z) \coloneqq\prod_{k\leq N}(z-p_k)\), and set \(F(z) \coloneqq g(z) f(z)\). Then \(F\) is an entire function, and the claim is that \(F\) is bounded and thus constant by Liouville. Proving the bound: take \({\left\lvert {z} \right\rvert} > R\), then \begin{align*} {\left\lvert {G(z)} \right\rvert} &= {\left\lvert {f(z)} \right\rvert} {\left\lvert {g(z)} \right\rvert} \\ &\leq M C {\left\lvert {z} \right\rvert}^N ,\end{align*} using that \(g\) is a polynomial of degree \(N\), so \({\left\lvert {g(z)\over z^N} \right\rvert}\to 1\) as \({\left\lvert {z} \right\rvert}\to \infty\) since \(g\) is monic. So after possibly increasing \(R\), we can choose \({\left\lvert {z} \right\rvert}\) large enough so that \({\left\lvert {g(z)\over z^N} \right\rvert} < C\) for, say, some constant \(C<2\). In any case, by a common qual question, if \({\left\lvert {G} \right\rvert} \in { \mathsf{O}} ({\left\lvert {z} \right\rvert}^N)\) for \({\left\lvert {z} \right\rvert}\) large enough then \(G\) is a polynomial of degree at most \(N\). Then \(f(z) \coloneqq G(z)/g(z)\) is a rational function.
Spring 2020 HW 3.5, Tie’s Extra Questions: Fall 2015
Let \(f\) be entire and suppose that \(\lim_{z \rightarrow \infty} f(z) = \infty\). Show that \(f\) is a polynomial.
Note that \(f\) has finitely many zeros: since \(f\) is unbounded, there is some \(R\) such that \(f({\mathbb{D}}_R^c) \subseteq {\mathbb{D}}^c\), so in particular \(f\) is nonvanishing on \({\mathbb{D}}_R^c\). So \(Z_f\) is a closed subset of a compact set, so is either finite or has an accumulation point. In the latter case, \(f\equiv 0\) by the identity principle, so suppose not.
Write \(Z_f = \left\{{z_k}\right\}_{k\leq n}\) for the \(n\) many zeros of \(f\), included with multiplicity, and set \begin{align*} \Phi(z) \coloneqq\prod_{k\leq n} (z-z_k), \qquad F(z) \coloneqq{\Phi(z) \over f(z) } .\end{align*} Now \(F\) is a nonvanishing entire function.
\(F\) is bounded on \({\mathbb{C}}\).
Choose \(R\gg 1\) so that all of \(z_k\) are in \({\mathbb{D}}_R\), so \({\left\lvert {\xi - z_k} \right\rvert} < R\) for all \(\xi \in {\mathbb{D}}_R\) and all \(k\). By Cauchy’s integral formula, \begin{align*} {\left\lvert {F(z)} \right\rvert} &\leq {1\over 2\pi} \oint_{{\left\lvert {\xi} \right\rvert} = R} {\left\lvert {F(\xi) \over \xi} \right\rvert} \,d\xi\\ &={1\over 2\pi} \oint_{{\left\lvert {\xi} \right\rvert} = R} {\left\lvert {\Psi(\xi) \over f(\xi) \cdot \xi} \right\rvert} \,d\xi\\ &\leq {1\over 2\pi} \oint_{{\left\lvert {\xi} \right\rvert} = R} {R^m \over {\left\lvert { f(\xi) } \right\rvert} R } \,d\xi\\ &\leq {1\over 2\pi} \oint_{{\left\lvert {\xi} \right\rvert} = R} R^{m-1} \,d\xi\\ &= R^m ,\end{align*} where \(R\) is increased if necessary to ensure \({\left\lvert {1\over f(z)} \right\rvert} < 1\), which can be done since \({\left\lvert {f(z)} \right\rvert}\to \infty\) as \(R\to \infty\). So \({\left\lvert {F(z)} \right\rvert} \leq C{\left\lvert {z} \right\rvert}^m\) in \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}_R\mkern-1.5mu}\mkern 1.5mu^c\) for \(R\) large enough, making \(F\) a polynomial of degree at most \(m\). Since \(F\) is continuous in \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}_R\mkern-1.5mu}\mkern 1.5mu\) which is compact, \(F\) is bounded in here as well, making \(F\) bounded on all of \({\mathbb{C}}\).
Given this, \(F\) is entire and bounded and thus constant by Liouville. So \(F(z) = c\), and as a result \(f(z) = c\Phi(z)\) which is a polynomial of degree \(n\).
Spring 2020 HW 2, SS 2.6.13
Suppose \(f\) is analytic, defined on all of \({\mathbb{C}}\), and for each \(z_0 \in {\mathbb{C}}\) there is at least one coefficient in the expansion \(f(z) = \sum_{n=0}^\infty c_n(z-z_0)^n\) is zero. Prove that \(f\) is a polynomial.
Hint: use the fact that \(c_n n! = f^{(n)}(z_0)\) and use a countability argument.
Write \(Z_n \coloneqq\left\{{z\in {\mathbb{C}}{~\mathrel{\Big\vert}~}f^{(n)}(z) = 0 }\right\}\), then by hypothesis \(\displaystyle\bigcup_{n\geq 0} Z_n = {\mathbb{C}}\). A version of the Baire category theorem is that if \(X\) is a complete metric space and \(X\) is a countable union of closed sets, then at least one such set has a nonempty interior. Thus some \(Z_n\) has an interior point \(z_0\), and as a result there is some disc \({\mathbb{D}}_{\varepsilon}(z_0)\) on which \(f^{(n)}(z_0) \equiv 0\). This implies that \(f^{(k)}(z_0) \equiv 0\) on \({\mathbb{D}}_{\varepsilon}(z_0)\) for every \(k\geq n\), so \(f\) is a polynomial of degree at most \(n\).
Rouché’s Theorem
Standard Applications
Tie’s Extra Questions: Fall 2009, Fall 2011, Spring 2014 (FTA)
Use Rouche’s theorem to prove the Fundamental Theorem of Algebra.
Write \(f(z) = \sum_{k\leq n} c_k z^k\). Big: \(M(z) = c_nz^n\). Small: \(m(z) = f(z) - M(z) = \sum_{k\leq n-1} c_k z^k\).
Now use that \begin{align*} {\left\lvert {m(z) \over M(z)} \right\rvert} &\coloneqq{\left\lvert {c_n^{-1}\sum_{k\leq n-1} c_k z^{k-n}} \right\rvert} \\ &= {\left\lvert {c_n^{-1}\qty{ {c_1\over z^n} + {c_2\over z^{n-1} } + \cdots + {c_{n-1}\over z} }} \right\rvert} \\ &\overset{{\left\lvert {z} \right\rvert}\to\infty}\longrightarrow 0 ,\end{align*} so choose \(R\) large enough such that for \({\left\lvert {z} \right\rvert} \geq R\), \({\left\lvert {M(z)\over m(z)} \right\rvert} < 1\). Then on \({\left\lvert {z} \right\rvert} = R\), \begin{align*} {\left\lvert {m(z) \over M(z)} \right\rvert} < 1 \implies {\left\lvert {m(z)} \right\rvert} < {\left\lvert {M(z)} \right\rvert} \implies {\sharp}n = {\sharp}Z_{M} = {\sharp}Z_{M+m} = {\sharp}Z_{f} ,\end{align*} since \(c_n z^n\) has \(z=0\) as a root with multiplicity \(n\).
An estimate: write \(f(z) = \sum_{k\leq n} c_k z^k\) with \(c_n = 1\), then for \(R> 1\), on \({\left\lvert {z} \right\rvert} = R\) we have \begin{align*} {\left\lvert {f(z) - z^n} \right\rvert} &\leq \sum_{k\leq n-1} {\left\lvert { c_k z^k} \right\rvert} \\ &\leq \sum_{k\leq n-1} {\left\lvert { c_k} \right\rvert} R^k \\ &\leq \sum_{k\leq n-1} {\left\lvert { c_k} \right\rvert} R^{n-1} \\ &= R^{n-1} \sum_{k\leq n-1} {\left\lvert { c_k} \right\rvert} \\ &\coloneqq R^{n-1} C \\ &\leq R^n \\ &= {\left\lvert {z^n} \right\rvert} ,\end{align*} provided we can choose \(C<R\), but this is possible since \(\sum_{k\leq n-1}{\left\lvert {c_k} \right\rvert}\) is a constant. So \(n = {\sharp}Z_{z^n} = {\sharp}Z_f\).
Tie’s Extra Questions: Fall 2015 (Standard polynomial)
Find the number of roots of \(z^4 - 6z + 3 =0\) in \(|z|<1\) and \(1 < |z| < 2\) respectively.
On \({\left\lvert {z} \right\rvert} \leq 1\):
- Big: \(M(z) = -6z\)
- Small: \(m(z) = z^4 + 3\)
Then on \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}^4 + 3 = 4 < 6 = {\left\lvert {-6z} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(1 = Z_M = Z_f\) here.
On \({\left\lvert {z} \right\rvert} \leq 2\):
- Big: \(M(z) = z^4\)
- Small: \(m(z) = -6z+3\).
Then on \({\left\lvert {z} \right\rvert} = 2\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {-6z + 3} \right\rvert} \leq 6{\left\lvert {z} \right\rvert} + 3 = 15 < 16 = 2^4 = {\left\lvert {z} \right\rvert}^4 = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(4 = Z_M = Z_f\) here.
Thus there are \(4-1 = 3\) zeros in \(1 \leq {\left\lvert {z} \right\rvert} \leq 2\).
Tie’s Extra Questions: Fall 2016 (Standard polynomial)
Prove that all the roots of the complex polynomial \begin{align*}f(z) = z^7 - 5 z^3 +12 =0\end{align*} lie between the circles \(|z|=1\) and \(|z|=2\).
On \({\left\lvert {z} \right\rvert} \leq 1\):
- Big: \(M(z) = 12\)
- Small: \(m(z) = z^6 - 5z^3\)
For \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} \coloneqq{\left\lvert {z^7-5z^3} \right\rvert}\leq {\left\lvert {z} \right\rvert}^7 + 5{\left\lvert {z} \right\rvert}^3 = 6 < 12 \coloneqq{\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(0 = Z_M = Z_{f}\).
On \({\left\lvert {z} \right\rvert} \leq 2\),
- Big: \(M(z) = z^7\)
- Small: \(m(z) = -5z^3 + 12\)
On \({\left\lvert {z} \right\rvert} = 2\), \begin{align*} {\left\lvert {m(z)} \right\rvert} \coloneqq{\left\lvert {-5z^3 + 12} \right\rvert} \leq 5{\left\lvert {z} \right\rvert}^2 + 12 = 32 < 128 = 2^7 \coloneqq{\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(7 = Z_M = Z_{f}\).
So \(f\) has 7 zeros in \(1 \leq {\left\lvert {z} \right\rvert} \leq 2\).
Spring 2020 HW 3.11 (Standard polynomial)
Find the number of roots of \(p(z) = z^4 - 6z + 3\) in \({\left\lvert {z} \right\rvert} < 1\) and \(1 < {\left\lvert {z} \right\rvert} < 2\) respectively.
Note: the original problem used \(4z^4-6z+3\), but I don’t think it’s possible to use Rouché on that at all!
On \({\left\lvert {z} \right\rvert} < 1\):
- Small: \(m(z) = z^4+3\)
- Big: \(M(z) = -6z\)
On \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {z^4+3} \right\rvert} \leq {\left\lvert {z} \right\rvert}^4 + 3 = 4 < 6 = {\left\lvert {-6z} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(Z_f = Z_M = 1\).
On \({\left\lvert {z} \right\rvert} < 2\):
- Small: \(-6z+3\)
- Big: \(z^4\)
On \({\left\lvert {z} \right\rvert} = 2\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = \leq 6 + 3 = 9 < 2^4 = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(Z_f = Z_M = 4\).
Thus there are \(4-1=3\) zeros in \(1 \leq {\left\lvert {z} \right\rvert} \leq 2\).
Standard polynomial
How many roots does the following polynomial have in the open disc \({\left\lvert {z} \right\rvert} < 1\)? \begin{align*} f(z) = z^7 - 4z^3 - 1 .\end{align*}
Big: \(M(z) = -4z^3\). Small: \(m(z) = z^7 - 1\). Then on \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {z^7-1} \right\rvert} \leq {\left\lvert {z} \right\rvert}^7 + 1 = 2 < 4 = {\left\lvert {-4z^4} \right\rvert} ,\end{align*} so \(f\) and \(M\) have the same number of zeros: three.
Spring 2020 HW 1.3 (Standard polynomial)
Prove that the following polynomial has its roots outside of the unit circle: \begin{align*} p(z) = z^3 + 2z + 4 .\end{align*}
Hint: What is the maximum value of the modulus of the first two terms if \({\left\lvert {z} \right\rvert} \leq 1\)?
Big: \(M(z) = 4\) Small: \(m(z) = z^3 + 2z\). On \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}^3 + 2{\left\lvert {z} \right\rvert} = 1+2=3 < 4 = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(0 = Z_M = Z_{M+m} = Z_f\) in \({\mathbb{D}}\).
Polynomials with parameters
Assume that \({\left\lvert {b} \right\rvert} < 1\) and show that the following polynomial has exactly two roots (counting multiplicity) in \({\left\lvert {z} \right\rvert} < 1\): \begin{align*} f(z) \coloneqq z^3 + 3z^2 + bz + b^2 .\end{align*}
Big: \(M(z) = 3z^2\). Small: \(m(z) = z^3+bz + b^2\). Then on \({\left\lvert {z} \right\rvert} = 1\): \begin{align*} {\left\lvert {m(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}^3 + b{\left\lvert {z} \right\rvert} + b^2 = 1 + b + b^2 < 3 = {\left\lvert {M(z)} \right\rvert} ,\end{align*} and \(M(z)\) has exact two roots in \({\mathbb{D}}\).
Tie’s Extra Questions: Spring 2015 (Power series)
Let \(0<r<1\). Show that polynomials \(P_n(z) = 1 + 2z + 3 z^2 + \cdots + n z^{n-1}\) have no zeros in \(|z|<r\) for all sufficiently large \(n\)’s.
Key observation: \begin{align*} P_n(z) = \sum_{1\leq k\leq n-1} kz^{k-1} = {\frac{\partial }{\partial z}\,}Q_n(z) \qquad Q(z) \coloneqq\sum_{0\leq k \leq n} z^k .\end{align*} Note that \(Q(z) \to \sum_{k\geq 0} z^k = {1\over 1-z}\) uniformly on \({\left\lvert {z} \right\rvert} \leq R < 1\) since this power series has radius of convergence 1. Similarly \(P_n(z)\) converges uniformly to \({\frac{\partial }{\partial z}\,}{1\over 1-z} = {1\over (1-z)^2}\), so let \(P(z) \coloneqq{1\over (1-z)^2}\). Note that \(P\) is nonvanishing in \({\mathbb{D}}\).
Strategy:
- Small: \(m(z) = P(z) - P_n(z)\), look for an upper bound \({\left\lvert {m(z)} \right\rvert} < U\)
- Big: \(P(z)\), look for a lower bound \(L\) with \({\left\lvert {P(z)} \right\rvert} > L > U\).
Just by considering the geometry of circles of radius \(R < 1\) and \(1\) and measuring distances to the point \(1\), we can estimate \begin{align*} 0 < 1-R \leq {\left\lvert {1-z} \right\rvert} < 1+R < 2 \implies {\left\lvert {P(z)} \right\rvert} = {1\over {\left\lvert {1-z} \right\rvert}^2} \geq {1\over 2^2} = {1\over 4} .\end{align*}
Now fix \({\varepsilon}< {1\over 4}\) and use uniform convergence of \(P_n\to P\) to produce an \(N\) such that \(n\geq N\) implies \({\left\lVert {P-P_n} \right\rVert}_\infty < {\varepsilon}\) in \({\left\lvert {z} \right\rvert} \leq R\). Then on \({\left\lvert {z} \right\rvert} = R\), for \(n\geq N\), \begin{align*} {\left\lvert {m(z)} \right\rvert} \coloneqq{\left\lvert {P(z) - P_n(z)} \right\rvert} \leq {\left\lVert {P - P_n} \right\rVert}_\infty < {\varepsilon}< {1\over 4} \leq {\left\lvert {P(z)} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(0 = Z_P = Z_{P_n}\) by Rouché.
Exponentials
UMN Fall 2009 (Solutions as zeros)
Find the number of solutions to the following equation on \({\left\lvert {z} \right\rvert} < 1\): \begin{align*} 6z^3 + 1 = -e^z .\end{align*}
Write \(f(z) \coloneqq 6z^3 + 1 + e^z\).
- Small: \(m(z) = e^z + 1\)
- Large: \(M(z) = 6z^3\)
- The estimate: \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {e^z + 1} \right\rvert} \leq e^{\Re(z)} + 1 \leq e^{{\left\lvert {z} \right\rvert}} + 1 = e+1 < 6 = {\left\lvert {6z^3} \right\rvert} ,\end{align*} so \(3 = Z_M = Z_f\).
UMN Spring 2009 (Checking the equality case)
Find the number of roots on \({\left\lvert {z} \right\rvert} \leq 1\) of \begin{align*} f(z)=z^{6}+4 z^{2} e^{z+1}-3 .\end{align*}
- Small: \(m(z) = z^6-3\)
- Big: \(M(z) = 4z^2 e^{z+1}\), which has two such zeros
Now estimate \(m\) from above: \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {z^6 - 3} \right\rvert} \leq {\left\lvert {z} \right\rvert}^6 + 3 = 4 .\end{align*} and \(M\) from below: \begin{align*} {\left\lvert {M(z)} \right\rvert} = {\left\lvert {4z^2 e^{z+1}} \right\rvert} = 4e{\left\lvert {z} \right\rvert}^4 e^{\Re(z)} = 4e e^{\Re(z)} \geq 4e e^{-1} = 4 ,\end{align*} which unfortunately isn’t quite enough. But equality occurs iff \(\Re(z) = -1\) on \(S^1\), so \(z=-1\), in which case \({\left\lvert {m(-1)} \right\rvert} = {\left\lvert {1-3} \right\rvert} = 2\), so the inequality is in fact strict. So \(2 = Z_M = Z_f\).
Right half-plane estimate
Find the number of zeros \(z\) with \(\Re(z) > 0\) for the following function: \begin{align*} f(z) \coloneqq z^3-z+1 .\end{align*}
Take a contour \(\gamma_1 \coloneqq\left\{{it {~\mathrel{\Big\vert}~}t\in {\mathbb{R}}}\right\}\) and \(\gamma_2\coloneqq\left\{{Re^{it} {~\mathrel{\Big\vert}~}t\in [-\pi, \pi]}\right\}\).
- Big: \(M(z) = z^3 + 1\)
- Small: \(m(z) = -z\)
On \(\gamma_2\), we have \({\left\lvert {z} \right\rvert} = R\), so take \(R\) large enough that the following estimate holds: \begin{align*} {\left\lvert {M(z)} \right\rvert} = {\left\lvert {z^3 + 1} \right\rvert} \geq {\left\lvert { {\left\lvert {z} \right\rvert}^3 - 1} \right\rvert} = R^3 - 1 > R = {\left\lvert {m(z)} \right\rvert} = R .\end{align*} In particular, this works for \(R> 1\).
On \(\gamma_1\), note
- \({\left\lvert {M(z)} \right\rvert} = {\left\lvert { (it)^3 + 1 } \right\rvert} = {\left\lvert {1-it^3} \right\rvert}\)
- \({\left\lvert {m(z)} \right\rvert} = {\left\lvert {it} \right\rvert}\)
These can be interpreted geometrically: the former is the hypotenuse of a triangle and the latter is a leg, so \({\left\lvert {M(z)} \right\rvert} \geq {\left\lvert {m(z)} \right\rvert}\) will hold:
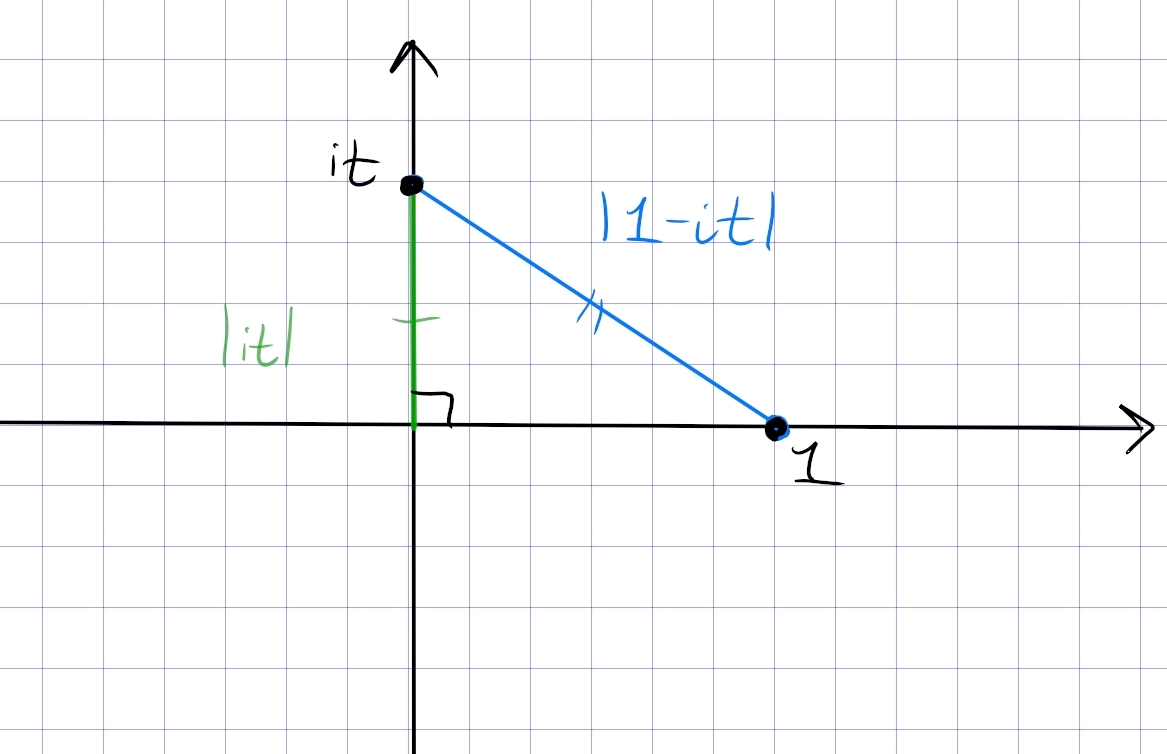
Now note that \(z^3 + 1\) has roots \(\omega_3, \omega_3^2, \omega_3^3=-1\) for \(\omega_k \coloneqq e^{i\pi\over k}\), and the first two are in the right half-plane. So \(2 = {\sharp}Z_M = {\sharp}Z_f\) by Rouché.
Zeros of \(e^z\)
Prove that for every \(n\in {\mathbb{Z}}^{\geq 0}\) the following polynomial has no roots in the open unit disc: \begin{align*} f_n(z) \coloneqq\sum_{k=0}^n {z^k \over k!} .\end{align*}
Hint: check \(n=1,2\) directly.
For the \(n=1\) case, \(f_1(z) = 0 \iff 1+z = 0 \iff z=-1\), so this has no roots in \({\mathbb{D}}\). For \(n=2\), factor \begin{align*} f_2(z) = 1 + z + z^2 = (z-\zeta_3^2)(z-\zeta_3^{-2}) ,\end{align*} using that \begin{align*} \zeta_3^2\cdot \zeta_3^{-2} = 1,\qquad -(\zeta_3^2 + \zeta_3^{-2}) = -2\Re(\zeta_3^2) = -2\cos\qty{2\pi \over 3} = 1 .\end{align*} Now use that \({\left\lvert {\zeta_3^{k}} \right\rvert} = 1\), which is not in \({\mathbb{D}}\).
For \(n\geq 3\): toward applying Rouche’s theorem, let \(M(z) = 1 + z\) and \(m(z) = {1\over 2}z^2 + \cdots + {1\over n!}z^n\). Note that on \({\left\lvert {z} \right\rvert} = 1\), \({\left\lvert {m(z)} \right\rvert} = 2\), and \begin{align*} {\left\lvert {m(z)} \right\rvert} &= {\left\lvert {\sum_{k\geq n+1} {z^k\over k!} } \right\rvert} \\ &\leq \sum_{k\geq n+1} { {\left\lvert {z} \right\rvert}^k \over k!} \\ &\leq \sum_{k\geq n+1} { 1 \over k!} \\ &= e^1 - \sum_{k\leq n} {1\over k!} .\end{align*} Suppose \(n\geq 3\), \begin{align*} {\left\lvert {m(z)} \right\rvert} < e - (1 + 1 + \cdots) \approx 0.718 < 2 ,\end{align*} then Rouché applies directly and \begin{align*} 0 = {\sharp}Z_M({\mathbb{D}}) ={\sharp}Z_{M+m}({\mathbb{D}}) \coloneqq{\sharp}Z_f({\mathbb{D}}) ,\end{align*} noting that \(M(z) = 0 \iff z= -1\), which isn’t contained in the open disc \({\mathbb{D}}\).
More \(e^z\)
Let \(n\in {\mathbb{Z}}^{\geq 0}\) and show that the equation \begin{align*} e^z = az^n \end{align*} has \(n\) solutions in the open unit disc if \({\left\lvert {a} \right\rvert} > e\), and no solutions if \({\left\lvert {a} \right\rvert} < {1\over e}\).
Note that \({\left\lvert {e^z} \right\rvert} = e^{\Re(z)}\), which is maximizes on \(S^1\) at \(z=1 \in {\mathbb{R}}\) and minimized at \(z=-1\). Write \(f(z) = e^z-az^n\), so solution correspond to zeros of \(f\).
Case 1: suppose \({\left\lvert {a} \right\rvert} > e\). Big: \(M(z) = az^n\). Small: \(m(z) = e^z\). On \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {e^z} \right\rvert} = e^\Re(z) \leq e^1 < {\left\lvert {a} \right\rvert} = {\left\lvert {az^n} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(f\) has \({\sharp}Z_M = n\) zeros.
Case 2: suppose \({\left\lvert {a} \right\rvert} < 1/e\). Big: \(M(z) = e^z\). Small: \(m(z) = az^n\). On \({\left\lvert {z} \right\rvert} = 1\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {az^n} \right\rvert} = {\left\lvert {a} \right\rvert} < e^{-1}\leq e^{\Re(z)} = {\left\lvert {e^z} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} and \(M\) has no zeros in \({\mathbb{D}}\) (and in fact none in \({\mathbb{C}}\)), so neither does \(f\).
Zeros of partial sums of exponential
For each \(n\in {\mathbb{Z}}^{\geq 1}\), let \begin{align*} P_n(z) = 1 + z + {1\over 2!} z^2 + \cdots + {1\over n!}z^n .\end{align*} Show that for sufficiently large \(n\), the polynomial \(P_n\) has no zeros in \({\left\lvert {z} \right\rvert} < 10\), while the polynomial \(P_n(z) - 1\) has precisely 3 zeros there.
More is true: this will hold for any disc of arbitrary radius \(R\), with \(n\) depending on \(R\). Fix \(R\), then use that \(P_n(z) \overset{n\to\infty}\longrightarrow e^z\) uniformly on the compact disc \({\left\lvert {z} \right\rvert} \leq R\). Consequently, setting \(g_n(z) \coloneqq{P_n(z)\over e^z}\), we have \(g_n(z) \to 1\) uniformly on this disc, for any \({\varepsilon}> 0\) this can be used to produce an \(n\gg 1\) such that \({\left\lvert { g_n(z) - 1 } \right\rvert} < {\varepsilon}\) for all \({\left\lvert {z} \right\rvert} \leq R\).
So take \({\varepsilon}\coloneqq 1\) and define \(h(z) \coloneqq 1\), then for \({\left\lvert {z} \right\rvert} = R\) \begin{align*} {\left\lvert {g_n(z) - 1} \right\rvert} < 1 = {\left\lvert {h(z)} \right\rvert} ,\end{align*} so by Rouché, \begin{align*} 0 = {\sharp}Z_{h} = {\sharp}Z_{h + (g_n - 1)} = {\sharp}Z_{g_n} ,\end{align*} since \(h\) has no zeros at all. Take \(R=10\) to get the stated result.
For \(P_n(z) - 1\), note that \(e^z-1=0\) has three solutions in \({\left\lvert {z} \right\rvert} < 10\), namely \(z=0, \pm 2\pi i\). We similarly have \(P_n(z)-1\to e^z-1\) uniformly, so on a disc of radius \(R\) choose \(n\) large enough so that \begin{align*} {\left\lvert {{P_n(z) -1 \over e^z - 1} - 1} \right\rvert} &< 1 \\ \implies {\left\lvert { (P_n(z) - 1) - (e^z-1) \over e^z-1} \right\rvert} &< 1 \\ \implies {\left\lvert { (P_n(z) - 1) - (e^z-1)} \right\rvert} &< {\left\lvert {e^z-1} \right\rvert} \\ \coloneqq{\left\lvert {m(z)} \right\rvert} &< {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \begin{align*} 3 = {\sharp}Z_M = {\sharp}Z_{M+m} = {\sharp}Z_{P_n - 1} .\end{align*}
Working for the estimate
Max of a polynomial on \(S^1\)
Prove that \begin{align*} \max_{{\left\lvert {z} \right\rvert} = 1} {\left\lvert {a_0 + a_1 z + \cdots + a_{n-1}z^{n-1} + z^n} \right\rvert} \geq 1 .\end{align*}
Hint: the first part of the problem asks for a statement of Rouche’s theorem.
Write \(p(z) \coloneqq a_0 + \cdots + z^n\). Toward a contradiction, suppose not so that \({\left\lvert {p(z)} \right\rvert} < 1\) on \({\left\lvert {z} \right\rvert} = 1\). Then \begin{align*} {\left\lvert {f(z)} \right\rvert} < 1 = {\left\lvert {z} \right\rvert}^n \qquad \text{ on } {\left\lvert {z} \right\rvert} = 1 .\end{align*} Taking \(m(z) \coloneqq f(z)\) and \(M(z) \coloneqq-z^n\), we have \begin{align*} n = {\sharp}Z_M = {\sharp}Z_{M+m} = {\sharp}Z_{f(z) - z^n} \leq n-1 ,\end{align*} since \(f(z) - z^n\) is degree at most \(n-1\), a contradiction.
Fixed points
Let \(c\in {\mathbb{C}}\) with \({\left\lvert {c} \right\rvert} < {1\over 3}\). Show that on the open set \(\left\{{z\in {\mathbb{C}}{~\mathrel{\Big\vert}~}\Re(z) < 1}\right\}\), the function \(f(z) \coloneqq ce^z\) has exactly one fixed point.
The boundary region is \(\left\{{1+it{~\mathrel{\Big\vert}~}t\in {\mathbb{R}}}\right\}\), write \(g(z) = ce^z-z\) so that fixed points of \(f\) are zeros of \(g\).
Big: \(M(z) = z\). Small: \(m(z) = ce^z\). Then for \(z=1+it\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {c} \right\rvert}e^{\Re(z)} < ce < 1 \leq \sqrt{1^2+t^2} = {\left\lvert {1+it} \right\rvert} = {\left\lvert {z} \right\rvert} ,\end{align*} so \(M\) and \(g\) have the same number of zeros, and \(M\) has a unique zero.
\(z\sin(z)=1\)
Show that \(z\sin(z) = a\) has only real solutions.
Consider \(f(z) \coloneqq z\sin(z) - a\).
Big: \(M(z) \coloneqq z\sin(z)\). Small: \(m(z) \coloneqq-a\). Use the following estimate: \begin{align*} {\left\lvert {z\sin(z)} \right\rvert}^2 &= {\left\lvert {z\over 2} \right\rvert}^2 {\left\lvert {e^{iz} - e^{-iz}} \right\rvert}^2 \\ &\geq {\left\lvert {z\over 2} \right\rvert}^2 {\left\lvert { {\left\lvert {e} \right\rvert}^{iz} } \right\rvert} - {\left\lvert { e^{-iz} } \right\rvert} }^2 \\ &= {\left\lvert {z\over 2} \right\rvert}^2 {\left\lvert {e^{-\Im(z)} - e^{\Im(z)} } \right\rvert} \\ &\overset{\Im(z)\to\infty}\longrightarrow \infty ,\end{align*} and so in particular a radius \(R\) can be chosen large enough so that \({\left\lvert {z\sin(z)} \right\rvert} > a\) for any \(a\). Thus for \({\left\lvert {z} \right\rvert} = R\), \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {a} \right\rvert} \leq {\left\lvert {z\sin(z)} \right\rvert} < {\left\lvert {M(z)} \right\rvert} \implies {\sharp}Z_{M} = {\sharp}Z_{M+m} = {\sharp}Z_f .\end{align*} To count the number of zeros of \(z\sin(z)\), note that this equals zero at \(z=0\) with multiplicity two and \(z= k\pi\) for \(k\in {\mathbb{Z}}\). Choosing \(R = {\pi \over 2} + n\pi\) for \(n\) large enough, there are exactly \(2n+2\) such zeros (with multiplicity) to \(z\sin(z)\), and thus \(2n+2\) zeros to \(z\sin(z) - a\). Now using that \(z\sin(z) - a\) has exactly \(2n+2\) real roots (??), this must be all of them.
Unsure how to find any roots of this thing, real or not!
Spring 2020 HW 3.13 #stuck
Prove that for \(a> 0\), \(z\tan z - a\) has only real roots.
UMN Spring 2011 (Constant coefficient trick)
Let \(a\in {\mathbb{C}}\) and \(n\geq 2\). Show that the following polynomial has one root in \({\left\lvert {z} \right\rvert} \leq 2\): \begin{align*} f(z) = az^n + z + 1 .\end{align*}
The key step: getting the following inequality to work \begin{align*} {\left\lvert {az^n} \right\rvert} = {\left\lvert {a} \right\rvert}{\left\lvert {z} \right\rvert}^n < c \leq 1 = {\left\lvert { {\left\lvert {z} \right\rvert} - {\left\lvert {1} \right\rvert} } \right\rvert} \leq {\left\lvert {z+1} \right\rvert} .\end{align*} If this is true, then \(1 = {\sharp}Z_{z+1} = {\sharp}Z_f\). If \({\left\lvert {a} \right\rvert} < 2^n\), this holds because \({\left\lvert {a} \right\rvert}{\left\lvert {z} \right\rvert}^n < {1\over 2^n} 2^n = 1\), so taking \(c\coloneqq 1\) works.
Otherwise, suppose \({\left\lvert {a} \right\rvert} \geq 2^n\). Letting \(z_k\) be the roots of \(f\) and considering the constant coefficient, we have \begin{align*} a\prod_{k\leq n} z_k = 1 \implies {\left\lvert { \prod_{k\leq n} z_k } \right\rvert} = {\left\lvert {1\over a} \right\rvert} \leq 2^n ,\end{align*} so not every \(z_k\) can satisfy \({\left\lvert {z_k} \right\rvert} > 2\) and at least one is in \({\left\lvert {z} \right\rvert} \leq 2\).
Argument Principle
Spring 2020 HW 3.12, Tie’s Extra Questions Fall 2015 (Root counting with argument principle)
Prove that \(f(z) = z^4 + 2z^3 -2z + 10\) has exactly one root in each open quadrant.
Take a large semicircle
-
\(\gamma_1 = [0, R]\)
-
\(\gamma_2 = \left\{{Re^{it} {~\mathrel{\Big\vert}~}t\in [0, \pi/2]}\right\}\)
-
\(\gamma_3 = i[0, R]\)
-
\(\Delta\operatorname{Arg}(f, \gamma_1) = 0\): The only way \(f\circ \gamma_1\) can change argument is by changing sign, since it’s real valued. Use that \(f(0) = 10, f(1) = 11\) and \(f'(t) = 4t^3+6t-2 > 0\) so \(f\) is increasing on \([1, \infty)\). Then by Rouché, on \({\left\lvert {z} \right\rvert} = 1\) we have \({\left\lvert {z^4+2z^3-2} \right\rvert}\leq 5 < 10 = {\left\lvert {10} \right\rvert}\), so \(f\) has no zeros on \({\left\lvert {z} \right\rvert} \leq 1\).
-
\(\Delta\operatorname{Arg}(f, \gamma_2) = 2\pi\): parameterize \(\gamma_2(t) = Re^{it}\), then \(f(\gamma(t)) \sim R^4e^{it}\) for large \(R\), which changes argument by \(2\pi\) for \(t\) in \([0, \pi/2]\).
-
\(\Delta\operatorname{Arg}(f, \gamma_3) = 0\): check \(f(it) = t^4 + 10 + i(-2t^3-2t)\) and we let \(t\) range through \([0, R]\). For \(t>0\), the real part is strictly positive, so this can not wind about the origin.
By the argument principle, \({\sharp}Z_f = {1\over 2\pi} \Delta\operatorname{Arg}(f, \Gamma) = 1\).
It suffices to show there’s only one root in the open quadrant \(Q_1\), since they come in conjugate pairs. Assume that there are no roots on \({\mathbb{R}}\) or \(i{\mathbb{R}}\). Since polynomials are entire, the argument principle can be used to count zeros: \begin{align*} Z_f = {1\over 2\pi i}\int_\gamma { {\partial}^{\scriptsize \log} }f(z)\,dz= \Delta_\gamma \operatorname{Arg}(f) .\end{align*} To take the curve \(\gamma\) comprised of
- \(\gamma_1 = [0, R]\),
- \(\gamma_2 = Re^{it}\) for \(t\in [0, \pi/2]\)
- \(\gamma_3 = i[0, R]\).
Then
- \(\Delta_{\gamma_1}\operatorname{Arg}(f) = 0\), since \(f({\mathbb{R}}_{\geq 0}) \subseteq {\mathbb{R}}_{\geq 0}\).
- \(\Delta_{\gamma_2}\operatorname{Arg}(f) = 4\cdot {\pi\over 2} = 2\pi\) since \(f\sim z^4\) for large \(R\).
- \(\Delta_{\gamma_3}\operatorname{Arg}(f)\): consider \begin{align*} f(it) = t^4 - it^3 -2it + 10 = t^4\qty{1 - it^{-1}-2it^{-2} +10t^{-4}} \\ \implies \operatorname{Arg}(f(it)) \sim \operatorname{Arg}(t^4) =0 .\end{align*}
So \(\Delta_\gamma \operatorname{Arg}(f) = 1\), meaning there is one zero enclosed by \(\gamma\) for \(R\) large enough. As \(R\to \infty\), this covers \(Q_1\).
\(n\)-to-one functions
Let \(f\) be analytic in a domain \(D\) and fix \(z_0 \in D\) with \(w_0 \coloneqq f(z_0)\). Suppose \(z_0\) is a zero of \(f(z) - w_0\) with finite multiplicity \(m\). Show that there exists \(\delta >0\) and \({\varepsilon}> 0\) such that for each \(w\) such that \(0 < {\left\lvert {w-w_0} \right\rvert} < {\varepsilon}\), the equation \(f(z) - w = 0\) has exactly \(m\) distinct solutions inside the disc \({\left\lvert {z-z_0} \right\rvert} < \delta\).
Write \(g(z) \coloneqq f(z) - w_0\), then \(g\) is holomorphic on \(D\) and thus \(w_0\) is an isolated zero. Choose \(\delta\) small enough so that \(g\) is nonvanishing on \({\mathbb{D}}_\delta(z_0)\setminus\left\{{ z_0 }\right\}\). Let \begin{align*} \gamma \coloneqq\left\{{{\left\lvert {\xi - z_0} \right\rvert} = \delta }\right\}= {{\partial}}{\mathbb{D}}_{\delta}(z_0) .\end{align*} Choose \({\varepsilon}< \inf\left\{{w\in f(\delta)}\right\}\) so that \({\left\lvert {f(z) - w_0} \right\rvert} > {\varepsilon}\) in \({\mathbb{D}}_{\varepsilon}(w_0)\setminus\left\{{ w_0 }\right\}\) for every \(z\in \gamma\). Let \begin{align*} \gamma' \coloneqq{{\partial}}{\mathbb{D}}_{{\varepsilon}}(w_0) = \left\{{{\left\lvert {z-w_0} \right\rvert} = {\varepsilon}}\right\} ,\end{align*} and define the solution counting function: \begin{align*} F(w) \coloneqq{1\over 2\pi i} \oint_{\gamma'} { {\partial}^{\scriptsize \log} }(g(z)) \,dz = {1\over 2\pi i } \oint_{\gamma'} {g'(z)\over g(z) }\,dz = {1\over 2\pi i} \oint_{\gamma'} {f'(z)\over f(z) - w} \,dz ,\end{align*} which counts the zeros of \(g\) (since it has no poles) and consequently the number of solutions to \(f(z) = w\) in \({\mathbb{D}}_{\varepsilon}(w_0)\). This is now a continuous integer valued function on \({\mathbb{D}}_{\varepsilon}(w_0)\), and is thus constant. Since \(f(z_0) = w_0\) with \(z_0\) enclosed by \(\gamma\) and \(w_0\) enclosed by \(\gamma'\), the constant is exactly the multiplicity of the zero of \(f(z) - w_0\) at \(z_0\), which is \(m\).
Blaschke products are \(n\) to one
For \(k=1,2,\cdots, n\), suppose \({\left\lvert {a_k} \right\rvert} < 1\) and \begin{align*} f(z) \coloneqq\qty{z - a_1 \over 1 - \mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu_1 z} \qty{z-a_2 \over 1 - \mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu_2 z} \cdots \qty{z - a_n \over 1 - \mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu_n z} .\end{align*} Show that \(f(z) = b\) has \(n\) solutions in \({\left\lvert {z} \right\rvert} < 1\).
Note that \(f\) is holomorphic on \({\mathbb{D}}\) and \(S^1\), since the poles are at \(1/\mkern 1.5mu\overline{\mkern-1.5mua_k\mkern-1.5mu}\mkern 1.5mu\) and if \({\left\lvert {a_l} \right\rvert} < 1\) then \({\left\lvert {\mkern 1.5mu\overline{\mkern-1.5mua_k\mkern-1.5mu}\mkern 1.5mu} \right\rvert} > 1\). Fix \(b\), then define \(g_w(z) \coloneqq f(z) - w\) and form the solution counting function \begin{align*} F(w) \coloneqq{1\over 2\pi i}\oint_{S^1} { {\partial}^{\scriptsize \log} }g_w(z) \,dz = {1\over 2\pi i} \oint_{S^1} {f'(z) \over f(z)-w}\,dz .\end{align*} Start by computing \(F(0)\). \begin{align*} F(0) &= {1\over 2\pi i }\oint_{S^1} { {\partial}^{\scriptsize \log} }\prod_{1\leq k\leq n} \psi_{a_k}(z) \,dz\\ &= {1\over 2\pi i }\oint_{S^1} \sum_{1\leq k\leq n} { {\partial}^{\scriptsize \log} }\psi_{a_k}(z) \,dz\\ &= {1\over 2\pi i }\oint_{S^1} \sum_{1\leq k\leq n} \qty{1-{\left\lvert {a_k} \right\rvert}^2 \over (1-\mkern 1.5mu\overline{\mkern-1.5mua_k\mkern-1.5mu}\mkern 1.5mu z)^2} \qty{z-a_k \over 1-\mkern 1.5mu\overline{\mkern-1.5mua_k\mkern-1.5mu}\mkern 1.5mu z}^{-1}\,dz\\ &= {1\over 2\pi i }\oint_{S^1} \sum_{1\leq k\leq n} {1-{\left\lvert {a_k} \right\rvert}^2 \over (z-a_k)( 1-\mkern 1.5mu\overline{\mkern-1.5mua_k\mkern-1.5mu}\mkern 1.5muz) } \,dz\\ &= {1\over 2\pi i } \sum_{1\leq k\leq n} \oint_{S^1} {1-{\left\lvert {a_k} \right\rvert}^2 \over (z-a_k)( 1-\mkern 1.5mu\overline{\mkern-1.5mua_k\mkern-1.5mu}\mkern 1.5muz) } \,dz\\ &= {1\over 2\pi i } \sum_{1\leq k\leq n} 2\pi i \\ &= n ,\end{align*} where we’ve used that the integrand has a simple pole at \(a_k\) since \(1/\mkern 1.5mu\overline{\mkern-1.5mua_k\mkern-1.5mu}\mkern 1.5mu\in {\mathbb{D}}^c\). So the equation \(f(z) = 0\) has \(n\) solutions. Now use that \(F\) is a continuous function of \(w\) on \({\mathbb{D}}\) and integer valued, thus constant. So \(F(w) = n\) for any \(w\), meaning \(f(z) = w\) has \(n\) solutions in \({\mathbb{D}}\) for every \(w\).
Alternative: \(F\) continuously depends on the \(a_k\), so send them all to zero to get \(f(z) = z^n\) which trivially has \(n\) zeros.
Morera
Uniform limit theorem
Suppose \(\left\{{f_n}\right\}_{n\in {\mathbb{N}}}\) is a sequence of analytic functions on \({\mathbb{D}}\coloneqq\left\{{z\in {\mathbb{C}}{~\mathrel{\Big\vert}~}{\left\lvert {z} \right\rvert} < 1}\right\}\).
Show that if \(f_n\to g\) for some \(g: {\mathbb{D}}\to {\mathbb{C}}\) uniformly on every compact \(K\subset {\mathbb{D}}\), then \(g\) is analytic on \({\mathbb{D}}\).
By Morera’s theorem, it suffices to show \(\int_T f = 0\) for all triangles \(T \subseteq {\mathbb{D}}\). Noting that \(T\) is closed and bounded and thus compact, \(f_n\to g\) uniformly on \(T\). Since the \(f_n\) are holomorphic, \(\int_T f_n = 0\) for all \(n\), and thus \begin{align*} \int_T g = \int_T \lim f_n = \lim_n \int_T f_n = \lim_n 0 = 0 ,\end{align*} where moving the limit through the integral is justified by uniform convergence.
Fourier transforms are entire
Suppose that \(f: {\mathbb{R}}\to{\mathbb{R}}\) is a continuous function that vanishes outside of some finite interval. For each \(z\in {\mathbb{C}}\), define \begin{align*} g(z) = \int_{-\infty}^\infty f(t) e^{-izt} \,dt .\end{align*}
Show that \(g\) is entire.
By Fubini: \begin{align*} \oint_T g(z)\,dz &\coloneqq\oint_T \int_{\mathbb{R}}f(t)e^{-izt} \,dt\,dz\\ &\coloneqq\int_{\mathbb{R}}\oint_T f(t)e^{-izt} \,dz\,dt\\ &\coloneqq\int_{\mathbb{R}}f(t) \qty{ \oint_T e^{-izt} \,dz} \,dt\\ &\coloneqq\int_{\mathbb{R}}f(t) \cdot 0 \,dt\\ &= 0 ,\end{align*} where the inner integral vanishes because \(z\mapsto e^{-izt}\) is entire by Goursat’s theorem. So \(g\) is entire by Morera.
Tie’s Extra Questions: Fall 2009, Fall 2011
Let \(f(z)\) be analytic in an open set \(\Omega\) except possibly at a point \(z_0\) inside \(\Omega\). Show that if \(f(z)\) is bounded in near \(z_0\), then \(\displaystyle \int_\Delta f(z) dz = 0\) for all triangles \(\Delta\) in \(\Omega\).
Write \({\mathbb{D}}_{\varepsilon}(z_0)\) for a disc in which \(f\) is bounded, say by \({\left\lvert {f} \right\rvert}\leq M\) here. Note that if \(z_0\) is not in the region enclosed by \(\Delta\), then \(\int_\Delta f = 0\) since \(f\) is holomorphic throughout \(\Delta\), so suppose \(z_0\) is in this region.
Since \(f\) is holomorphic in \(\Omega\setminus\left\{{ z_0 }\right\}\), \(\Delta\) can be deformed to \({{\partial}}{\mathbb{D}}_{\varepsilon}(z_0)\) without changing the integral. So \begin{align*} {\left\lvert { \oint_\Delta f } \right\rvert} &= {\left\lvert {\oint_{{{\partial}}{\mathbb{D}}_{\varepsilon}(z_0)} f } \right\rvert} \\ &\leq \oint_{{{\partial}}{\mathbb{D}}_{\varepsilon}(z_0)} {\left\lvert {f} \right\rvert} \\ &\leq \oint_{{{\partial}}{\mathbb{D}}_{\varepsilon}(z_0)} M \\ &= M\cdot 2\pi {\varepsilon}\\ &\overset{{\varepsilon}\to 0}\longrightarrow 0 ,\end{align*} noting that the bound \(M\) is constant and remains an upper bound on smaller discs by the maximum modulus principle.
Fall 2021.2
^a550c1
Let \(\gamma(t)\) be a piecewise smooth curve in \(\mathbb{C}, t \in[0,1]\). Let \(F(w)\) be a continuous function on \(\gamma\). Show that \(f(z)\) defined by \begin{align*} f(z):=\int_{\gamma} \frac{F(w)}{w-z} d w \end{align*} is analytic on the complement of the curve \(\gamma\).
By Morera’s theorem, it suffices to show \(\int_\Delta f(z) \,dz= 0\) for all triangles \(\Delta \subseteq \gamma^c\). Claim: \begin{align*} \int_\Delta f(z) \,dz &= \int_\Delta \int_\gamma {F(w) \over w-z} \,dw\,dz\\ &= \int_\gamma \int_\Delta {F(w) \over w-z} \,dz\,dw\\ &= \int_\gamma F(w) \qty{ \int_\Delta {1 \over w-z} \,dz} \,dw\\ &= \int_\gamma F(w) \cdot 0 \,dw\\ &= 0 .\end{align*}
That the inner integral is zero follows from the fact that the function \(z\mapsto {1\over w-z}\) is holomorphic on \(\gamma^c\), since it has only a simple pole at \(w\) where \(w\in \gamma\) is fixed.
That the interchange of integrals is justified follows from Fubini’s theorem: these are continuous functions on compact sets, which are uniformly bounded and thus Lebesgue measurable and integrable.
The claim is that \(f\) is complex differentiable, thus smooth, thus holomorphic and equal to its Taylor series expansion. The quick justification: \begin{align*} {\frac{\partial }{\partial z}\,} f(z) &= {\frac{\partial }{\partial z}\,} \int_\gamma {F(w) \over w-z}\,dw\\ &= \int_\gamma {\frac{\partial }{\partial z}\,} {F(w) \over w-z} \,dw\\ &= \int_\gamma {F(w) \over (w-z)^2} \,dw ,\end{align*} where differentiating through the integral is justified since the integrand is a continuous function of \(z\) on \(\gamma\) since \(w\neq z\) on \(\gamma\), and \(\gamma\) is a compact set.
Slightly more rigorously, one can equivalently pass a limit through the integral to show that the defining limit exists: \begin{align*} f(z+h) - f(z) &= \int_\gamma {F(w) \over w+h-z} \,dw- \int_\gamma {F(w) \over w-z}\,dw\\ &= \int_\gamma {(w-z)F(w) - (w+h-z)F(w) \over (w+h-z)(w-z) } \,dw\\ &= \int_\gamma F(w) {h \over (w+h-z)(w-z)} \,dw\\ &\overset{h\to 0}\longrightarrow \int_\gamma {F(w) \over (w-z)^2}\,dw ,\end{align*} since the term involving \(h\) goes to 1.
Spring 2020 HW 2, SS 2.6.6
Suppose that \(f\) is holomorphic on a punctured open set \(\Omega\setminus\left\{{w_0}\right\}\) and let \(T\subset \Omega\) be a triangle containing \(w_0\). Prove that if \(f\) is bounded near \(w_0\), then \(\int_T f(z) ~dz = 0\).
Without loss of generality assume \(w_0 = 0\). If \({\left\lvert {f(z)} \right\rvert} \leq M\) for \({\left\lvert {z} \right\rvert} < {\varepsilon}\), pick \(T\) contained in \({\mathbb{D}}_{\varepsilon}\), then \begin{align*} {\left\lvert {\oint_T f(z)\,dz} \right\rvert} \leq \oint_T {\left\lvert {f(z)} \right\rvert}\,dz\leq \oint_T M \,dz= M \mu(T) ,\end{align*} and by homotopy invariance, this integral doesn’t change as \(T\) is perturbed. Shrinking \(T\), we can make \(\mu(T)\to 0\).
See also conformal map exercises.
Classifying conformal maps
Define \begin{align*} G \coloneqq\left\{{z\in {\mathbb{C}}{~\mathrel{\Big\vert}~}\Re(z) > 0, \, {\left\lvert {z-1} \right\rvert} > 1}\right\} .\end{align*}
Find all of the injective conformal maps \(G\to {\mathbb{D}}\). These may be expressed as compositions of maps, but explain why this list is complete.
Use that every element of \(\mathop{\mathrm{Aut}}({\mathbb{D}})\) is of the form \(f(z) = \lambda\psi_a(z)\), and the region \(G\) is conformally equivalent to \({\mathbb{D}}\). Thus every element of \(\mathop{\mathrm{Aut}}(G)\) can be conjugated to an element of \(\mathop{\mathrm{Aut}}({\mathbb{D}})\) by a conformal map \(F: G\to {\mathbb{D}}\). One such map is gotten by rotating \(z\mapsto iz\) to get \({\mathbb{H}}\cap{\left\lvert {z} \right\rvert}>1\), then applying a Joukowski map \(z\mapsto z+z^{-1}\) to get \({\mathbb{H}}\). So \begin{align*} f\in \mathop{\mathrm{Aut}}(G) \implies f = F^{-1}\circ \psi_{a} \circ F \text{ for some } \psi_a \in \mathop{\mathrm{Aut}}({\mathbb{D}}) .\end{align*}
Half-planes, discs, strips
Tie’s Extra Questions: Spring 2015 (Good Practice)
Find a conformal map
-
from \(\{ z: |z - 1/2| > 1/2, \text{Re}(z)>0 \}\) to \(\mathbb H\)
-
from \(\{ z: |z - 1/2| > 1/2, |z| <1 \}\) to \(\mathbb D\)
-
from the intersection of the disk \(|z + i| < \sqrt{2}\) with \({\mathbb H}\) to \({\mathbb D}\).
-
from \({\mathbb D} \backslash [a, 1)\) to \({\mathbb D} \backslash [0, 1)\) (\(0<a<1)\).
Short solution possible using Blaschke factors.
-
from \(\{ z: |z| < 1, \text{Re}(z) > 0 \} \backslash (0, 1/2]\) to \(\mathbb H\).
Part 1: this is a bigon with vertices \(0, \infty\), so send \(0\to\infty\) with \(1/z\). Orient \(i{\mathbb{R}}\) and the circle \(S\) positively, note that both will be mapped to generalized circles. To find the resulting region, use handedness – it’s on the right of \(i{\mathbb{R}}\) and the right of \(S\). The map preserves \(i{\mathbb{R}}\) and as \(t\) traces out \((-\infty, 0^-, 0^+, \infty)\), \(f(it)\) traces out \((0^+, \infty, -\infty, 0^-)\), so this preserves the orientation of \(i{\mathbb{R}}\). For \(S\), let \(z_0\coloneqq{1\over 2}(1+i)\in S\), then \(f(z_0) = 1-i\). So the arc \((1,z_0, 0)\) maps to \((1, 1-i,\infty)\), so this is a vertical line through \(\Re(z) = 1\) oriented downward. The region is to the right of \(S\), so we have
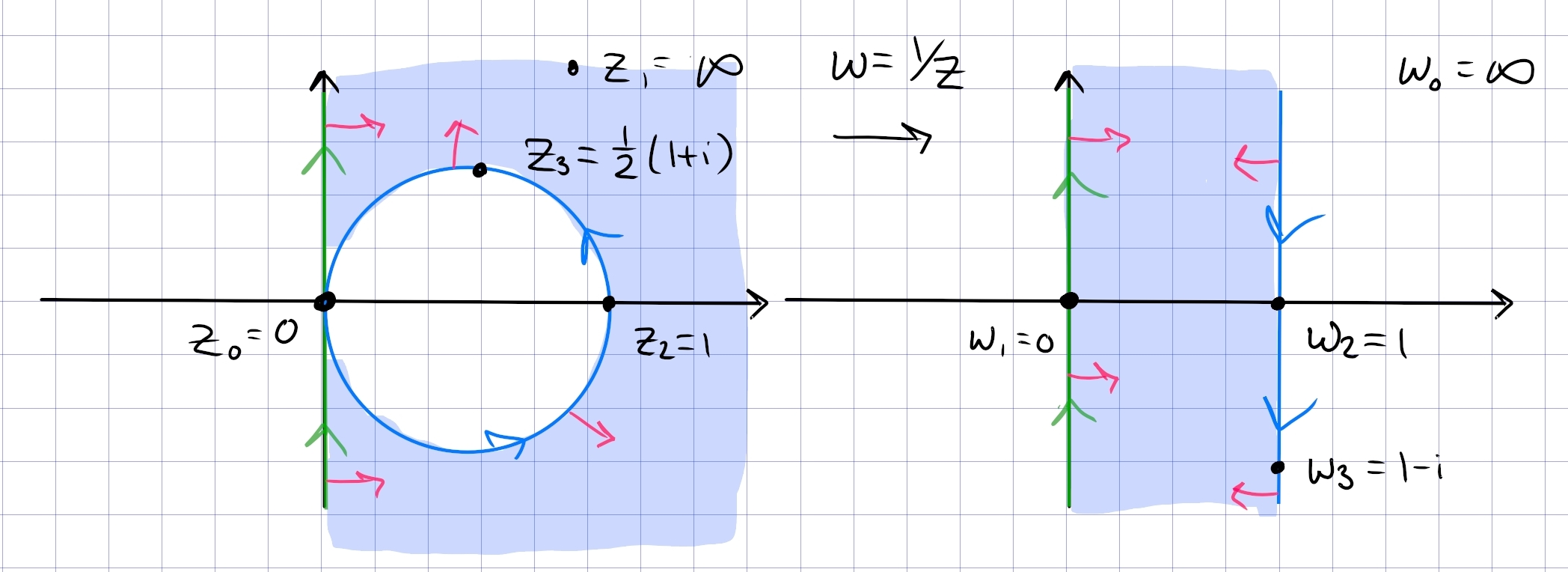
The rest is standard:
- Dilate and rotate to \(0<\Im(z) < \pi\) using \(z\mapsto i\pi z\).
-
Exponentiate using \(z\mapsto e^z\)
\to
get \({\mathbb{H}}\). - Apply the Cayley map \(z\mapsto {z-i\over z+i}\) to get \({\mathbb{D}}\).
Part 2: a bigon with vertex \(1\), i.e. a lune. Send \(1\to \infty\) with \(f(z) \coloneqq{1\over z-1}\), and check that
- \(1\mapsto \infty\)
- \({1\over 2}(1+i) \mapsto -(1+i)\)
- \(0\mapsto -1\)
- \(i\mapsto -{1\over 2}(1+i)\)
- \(-1\mapsto -{1\over 2}\)
By tracking tangent/normal vectors, this results in the region \(-1<\Re(z) < -{1\over 2}\):
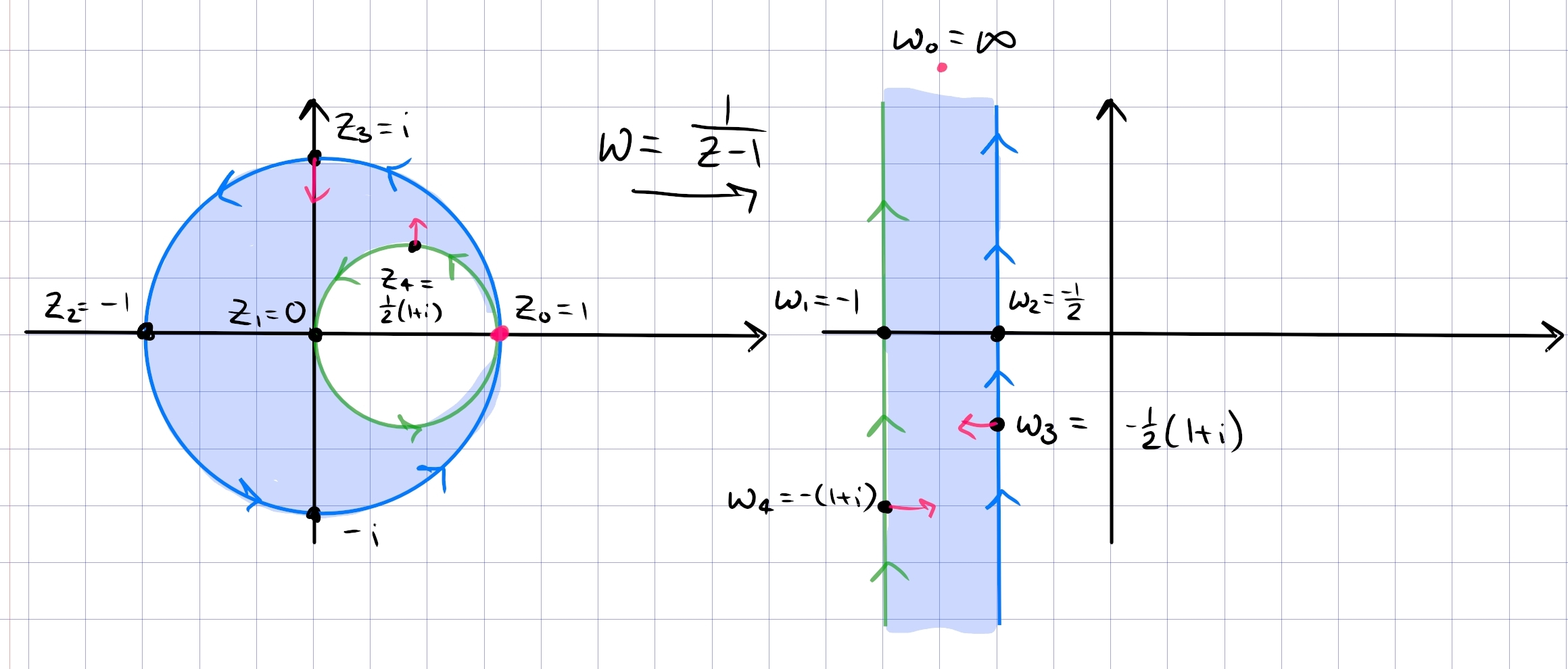
The rest is standard:
- Translate to the right by \(z\mapsto z+{1\over 2}\) to get \(-{1\over 2}<\Re(z) < 0\).
- Rotate and dilate by \(z\mapsto -2i\pi z\) to get \(0<\Im(z) < \pi\)
- Exponentiate by \(z\mapsto e^z\) to get \({\mathbb{H}}\),
- Cayley map \(z\mapsto {z-i\over z+i}\) to get \({\mathbb{D}}\).
Part 3: a bigon in \({\mathbb{H}}\) with vertices \(\pm 1\), with an arc passing through \(z_3 \coloneqq i(\sqrt{2} - 1)\). Take \(z\mapsto {z+1\over z-1}\) to obtain
- \(-1\mapsto 0\)
- \(1\mapsto \infty\)
- \(0\mapsto -1\)
\(z_3\mapsto w_0\) where \(\arg(w_0) = -3\pi/4\)
Let \(z_3 = ic\) where \(c\coloneqq\sqrt{2} -1\), then \begin{align*} f(z_3) &= -{1+z_3\over 1-z_3} \\ &= -{1+ic \over 1-ic} \\ &= -{(1+ic)^2 \over 1+c^2} \\ &= -\qty{ {1-c^2 \over 1+c^2} + i{2c\over 1+c^2} } .\end{align*} Now check that \(c^2 = 3-2\sqrt 2\) and \(1-c^2 = -2+2\sqrt{2}\), so \begin{align*} { 2c\over 1-c^2} = {2(\sqrt 2 - 1) \over -2 + 2\sqrt 2 } = 1 ,\end{align*} so the argument is \(\arctan(1) = { \pi \over 4}\) or \(-{3\pi \over 4}\). Since \(1-c^2>0, 2c>0\), noting the negative sign above, \(f(z_3)\) is in \(Q_3\), so take \(-3\pi \over 4\).
Orienting the bigon positively, we have \((-1, 0, 1)\mapsto (0, -1, \infty)\), i.e. the real axis oriented from \(+\infty\to-\infty\). Similarly \((1, z_3, -1)\mapsto (\infty, \omega_4^3, 0)\), which is a line passing through \(\omega_4^3\), oriented from \(Q_3\to Q_1\). Since the original region was on the left of both curves, we get
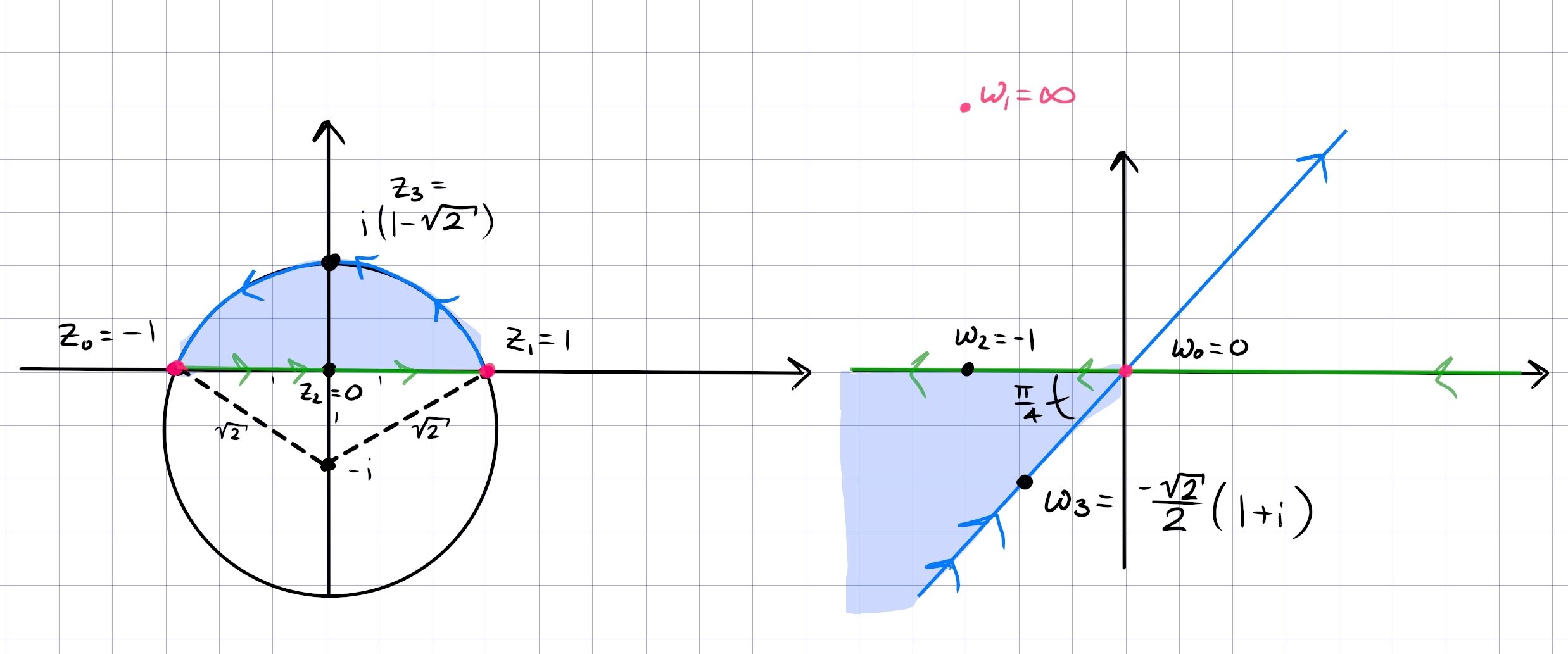
Now
- Flip this to \(Q_1\) with \(z\mapsto -z\) to get \(0<\operatorname{Arg}(z) < \pi/4\).
- Rotate clockwise with \(z\mapsto e^{-i\pi\over 8}\) to get \(-\pi/8<\operatorname{Arg}(z) < \pi/8\).
- Dilate the argument to a half-plane with \(z\mapsto z^{\pi\over 2\theta_0}\) where \(\theta_0 = \pi/8\) to get \(-\pi/2<\operatorname{Arg}(z) < \pi/2\).
- Rotate with \(z\mapsto iz\) to get \({\mathbb{H}}\).
- Cayley map, \(z\mapsto {z-i\over z+i}\).
Part 4: See part 5. The critical step is a Blaschke map \(\psi_a\) which sends \(a\to 0\). For \(a\in {\mathbb{R}}\), \(\psi_a({\mathbb{R}}) = {\mathbb{R}}\) and this will map the partial slit from \(a\) to the boundary to a usual slit from \(0\) to the boundary.
Part 5: Dealing with the slit:
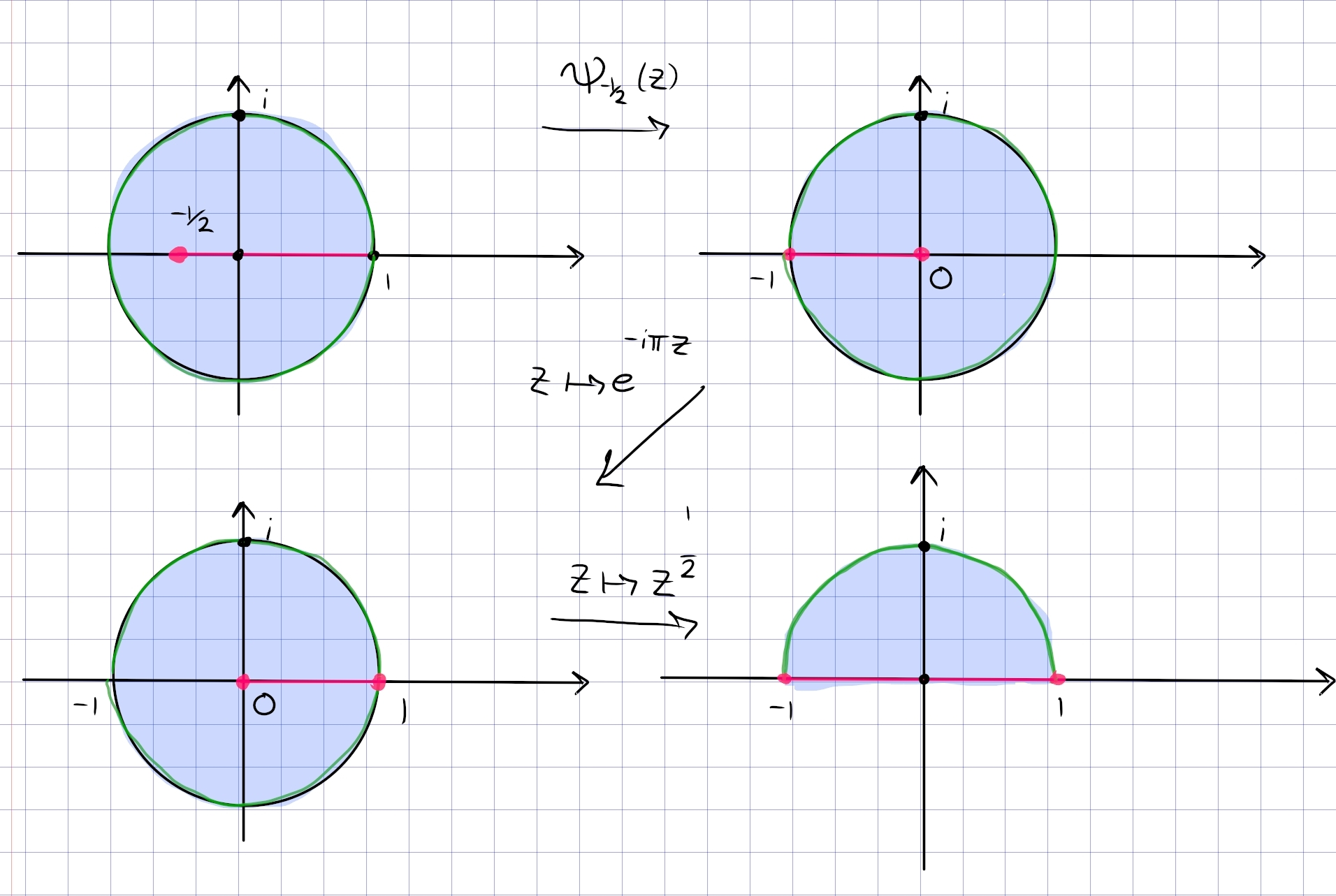
- Use a Blaschke factor to send \(a\coloneqq-1/2\to 0\), so \(z\mapsto {a-z\over 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu z}\). Checking that \((-1/2, 0, 1)\to (0, -1/2, -1)\), the image is \({\mathbb{D}}\setminus(-1, 0]\).
- Rotate with \(z\mapsto e^{-i\pi}z\) to get \({\mathbb{D}}\setminus[0, 1)\).
- Unfold with \(z\mapsto z^{1\over 2}\) to get \({\mathbb{D}}\cap{\mathbb{H}}\), noting that the slit becomes \([-1, 1]\) and is erased here.
- Use \(z\mapsto -1/z\) to get \({\mathbb{D}}^c \cap{\mathbb{H}}\).
- Use the Joukowski map \(z\mapsto z+z^{-1}\) to map to \(Q_{34}\)
- Use \(z\mapsto -z\) to get \({\mathbb{H}}\).
Tie’s Extra Questions: Fall 2016 (Half-strip)
Find the conformal map that takes the upper half-plane conformally onto the half-strip \begin{align*} \left\{{w=x+iy {~\mathrel{\Big\vert}~}-\pi/2 < x < \pi/2,\, y>0}\right\} .\end{align*}
It’s well known that \(z\mapsto \sin(z)\) sends \(-\pi/2<\Re(z) < \pi/2\) with \(\Im(z) > 0\) to \({\mathbb{H}}\):
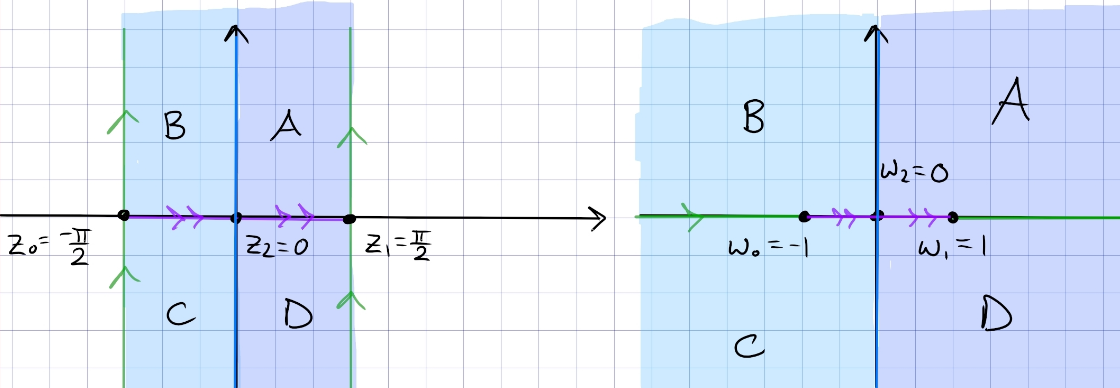
So take \(z\mapsto \arcsin(z)\).
Lunes, Bigons
Fall 2019.5, Tie’s extra questions: Fall 2009, Fall 2011, Spring 2014, Spring 2015
^043381
Find a conformal map from \begin{align*} D=\left\{{ z\in {\mathbb{C}}{~\mathrel{\Big\vert}~}|z|<1 \text{ and } {\left\lvert { z-{1\over 2}} \right\rvert}>{1\over 2}}\right\} \end{align*} to the unit disk \(\Delta=\{z:|z|<1\}\).
This is a lune-type region:
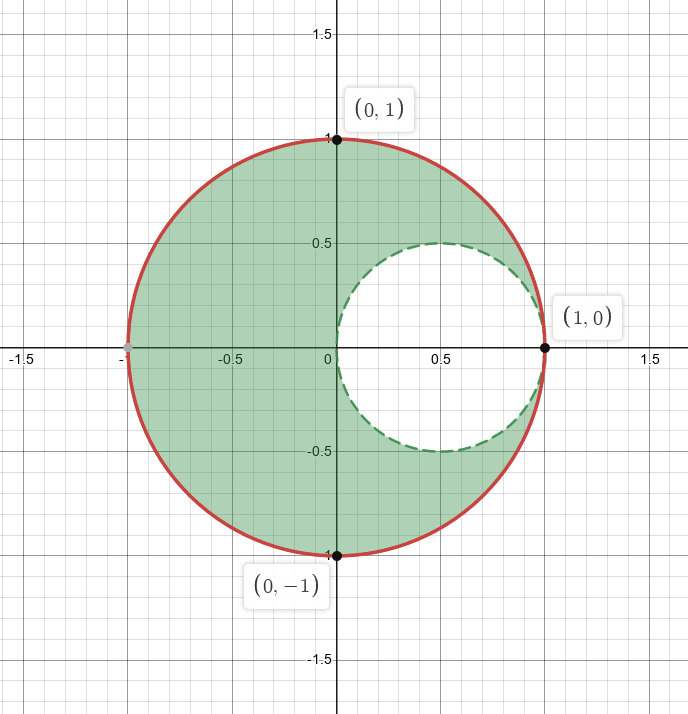
The usual strategy is to blow up the tangency, so send \(1\to\infty\) with \begin{align*} f(z) \coloneqq{1\over z-1} .\end{align*}
\(f\) has the following effect:
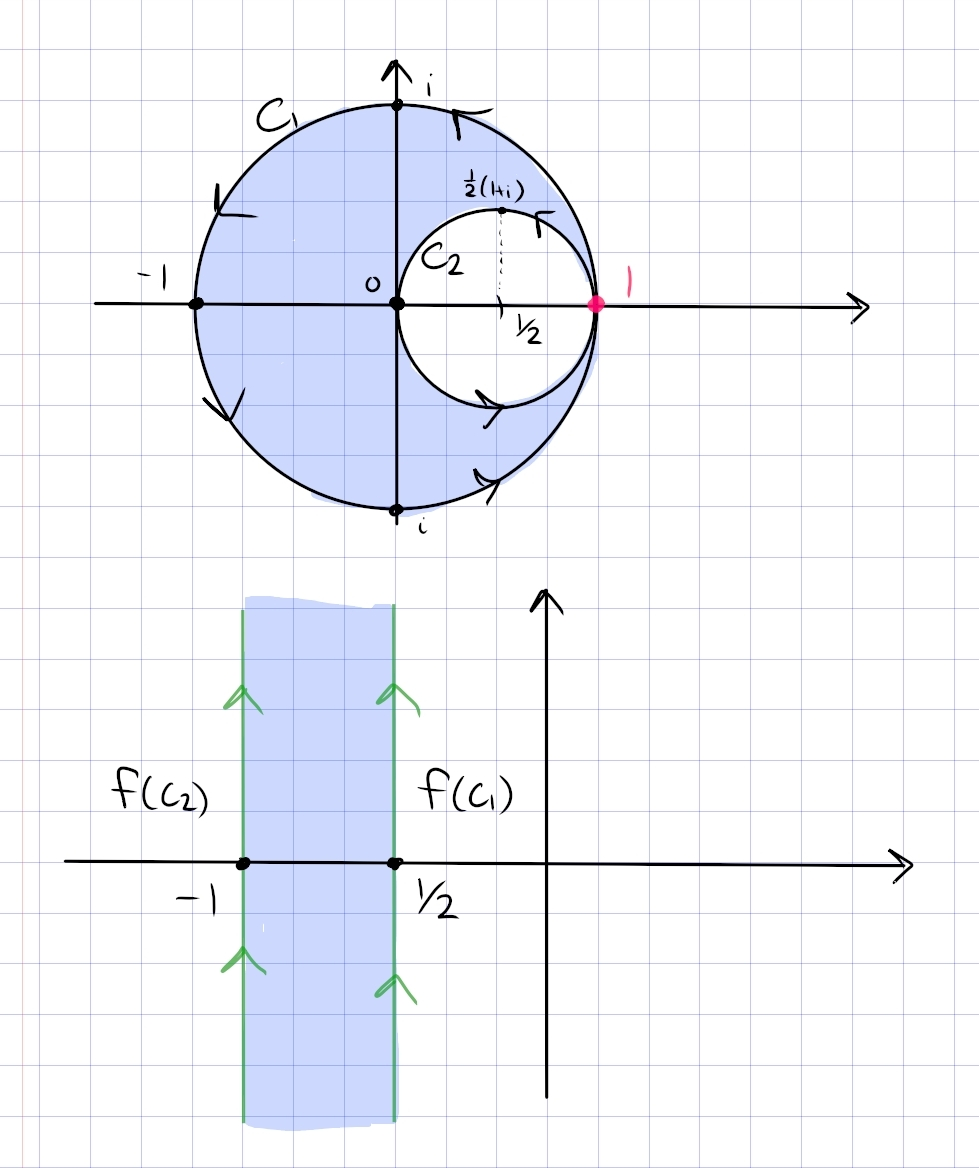
Write \(C_1\) for \(S^1\) and \(C_2\) for the smaller circle. Computing the image of \(C_1\): parameterize as \(\gamma_1(t) = e^{it}\) for \(t\in [-\pi, \pi]\), then \begin{align*} f(\gamma_1(t)) &= {1\over e^{it} - 1} \\ &= {e^{-it/2} \over e^{it/2} - e^{-it/2}} \\ &= {e^{-it/2} \over 2i\sin(t/2) } \\ &= -{i\over 2}\csc(t/2)\qty{\cos(t/2) - i\sin(t/2)} \\ &= -{i\over 2}\qty{\cot(t/2) - i } \\ &= {1\over 2}\qty{-1-i\cot(t/2)} \\ &= -{1\over 2} - i\cdot {1\over 2}\cot(t/2) .\end{align*}
Some analysis on \(\cot(t/2)\):
- \(-\pi\nearrow 0 \leadsto 0\searrow-\infty\)
- \(0\nearrow\pi \leadsto \infty\searrow 0\)
Thus for \(-\cot(t/2)\),
- \(-\pi\nearrow 0 \leadsto 0\nearrow\infty\)
- \(0\nearrow\pi \leadsto -\infty\nearrow 0\)
So the image is a vertical line through \(\Re(z) = -{1\over 2}\) oriented from \(-\infty\to\infty\).
For the image of \(C_2\): parameterize as \(\gamma_2(t) = {1\over 2}\qty{1 + e^{it}}\), then \begin{align*} f(\gamma_2(t)) &= {1\over {1\over 2}\qty{1+e^{it}} - 1 } \\ &= {1\over -{1\over 2} + {1\over 2}e^{it} } \\ &= {1\over {1\over 2}\qty{e^{it} - 1}} \\ &= {2e^{-it/2} \over e^{it/2} - e^{-it/2} } \\ &= {2e^{-it/2} \over 2i\sin(t/2) } \\ &= -i\csc(t/2) \qty{\cos(-t/2) + i\sin(-t/2) } \\ &= -i\csc(t/2) \qty{\cos(t/2) - i\sin(t/2) } \\ &= -i \qty{\cot(t/2) - i } \\ &= -1 - i\cot(t/2) .\end{align*} By the same argument as above, this traces out a vertical line at \(\Re(z) = -1\).
By handedness, since the original region is on the left with respect to \(C_1\) and the right with respect to \(C_2\), the new region is to the left of \(\Re(z) = -{1\over 2}\) and the right of \(\Re(z) = -1\) (since both are oriented from \(-\infty\) to \(\infty\)).
From here, it’s a standard exercise. In steps:
- Map \(R\) to the vertical strip \(-1< \Re(z) < -{1\over 2}\) using \(z\mapsto {1\over z-1}\).
- Shift using \(z\mapsto z+{1\over 2}\) to send this to \(-{1\over 2}< \Re(z) < 0\).
- Rotate using \(z\mapsto -iz\) to get \(0<\Im(z) < {i\over 2}\), a horizontal strip.
- Dilate using \(z\mapsto 2\pi z\), which sends \({i\over 2}\to \pi i\), so the resulting region is \(0 < \Im(z) < \pi\).
- Apply \(z\mapsto e^z\) to map the horizontal strip to \({\mathbb{H}}\).
- Apply the Cayley map \(z\mapsto {z-i\over z+i}\) to map \({\mathbb{H}}\to{\mathbb{D}}\).
Fall 2021.7
^efdbde
Find a conformal map from the intersection of \(|z-1|<2\) and \(|z+1|<2\) to the upper half plane.
DZG: I’m 90% sure this is meant to be \({\left\lvert {z-1} \right\rvert}, {\left\lvert {z+1} \right\rvert} < \sqrt{2}\) or \({\left\lvert {z-1} \right\rvert}^2,{\left\lvert {z+1} \right\rvert}^2 < 2\). Otherwise computing the argument of the resulting lines is tricky…
The region:
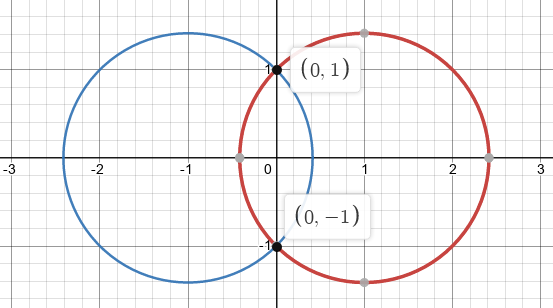
Note that you can find that \(i, -i\) are the intersection points by noting that \(i{\mathbb{R}}\) is the perpendicular bisector through the line segment connecting the centers of the circles, then expanding \({\left\lvert {z-1} \right\rvert}^2 = (x-1)^2 + y^2 = 2\) and setting \(x=0\) to get \(y=\pm i\).
First rotate this by \(\pi/2\):
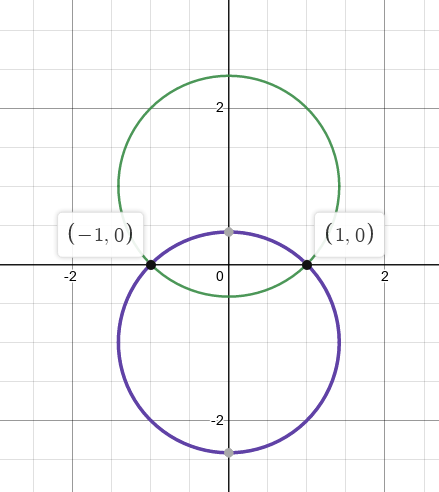
Call the upper circle \(C_1\) and the lower \(C_2\). Send \(-1\to 0, 1\to \infty\) by taking \begin{align*} f(z) \coloneqq{z+1\over z-1} .\end{align*} This sends the circles to lines through zero, and the lune now spans a triangular sector. Finding the angles of the lines: write \(c\coloneqq 1 + \sqrt{2}\). Note that \(f\) fixes \({\mathbb{R}}\), so the image regions are symmetric about \({\mathbb{R}}\), and it suffices to find the angle of the line \(f(C_1)\). Note that \(C_1 \cap i{\mathbb{R}}= ic\), so we compute \(\operatorname{Arg}(f(ic))\): \begin{align*} f(ic) &= {ic+1\over ic-1} \\ &= {(1+ic)^2 \over c^2 + 1} \\ &= {-1 + c^2 - 2ic \over c^2 + 1} \\ &= {c^2-1 \over c^2+1} -i {2c\over c^2+1} ,\end{align*} so \begin{align*} \operatorname{Arg}(f(ic)) &= \arctan\qty{ 2c\over -1 + c^2} \\ &= \arctan\qty{2(1+\sqrt 2) \over 1 - (3 + \sqrt 2)} \\ &= \arctan(-1) \\ &= {\pi\over 4} \text{ or } {3\pi \over 4} .\end{align*}
Thus \(f(C_1) = \left\{{te^{-i\pi\over 4} {~\mathrel{\Big\vert}~}t\in (-\infty, \infty)}\right\}\). Note that \(f(ic)\in Q_4\), since \(c^2-1, c^2+1 > 0\) and \({-2c\over c^2+1} < 0\). For the orientation of \(f(C_1)\), note that \((1, ic, -1) \mapsto (\infty, f(ic), 0)\), so the line is oriented from \(Q_4\) to \(Q_2\).
A similar computation shows \begin{align*} f(-ic) = {c^2-1\over c^2+1} + i{2\over c^2+1} \in Q_1 ,\end{align*} and \((-1, -ic, 1)\mapsto (0, f(-ic), \infty)\), so \(f(C_2)\) is oriented from \(Q_3\) to \(Q_1\).
Since the origin region was to the left of the curves, it remains to the left, so the resulting region is \(\left\{{z{~\mathrel{\Big\vert}~}3\pi/4 < \operatorname{Arg}(z) < 5\pi/4}\right\}\):
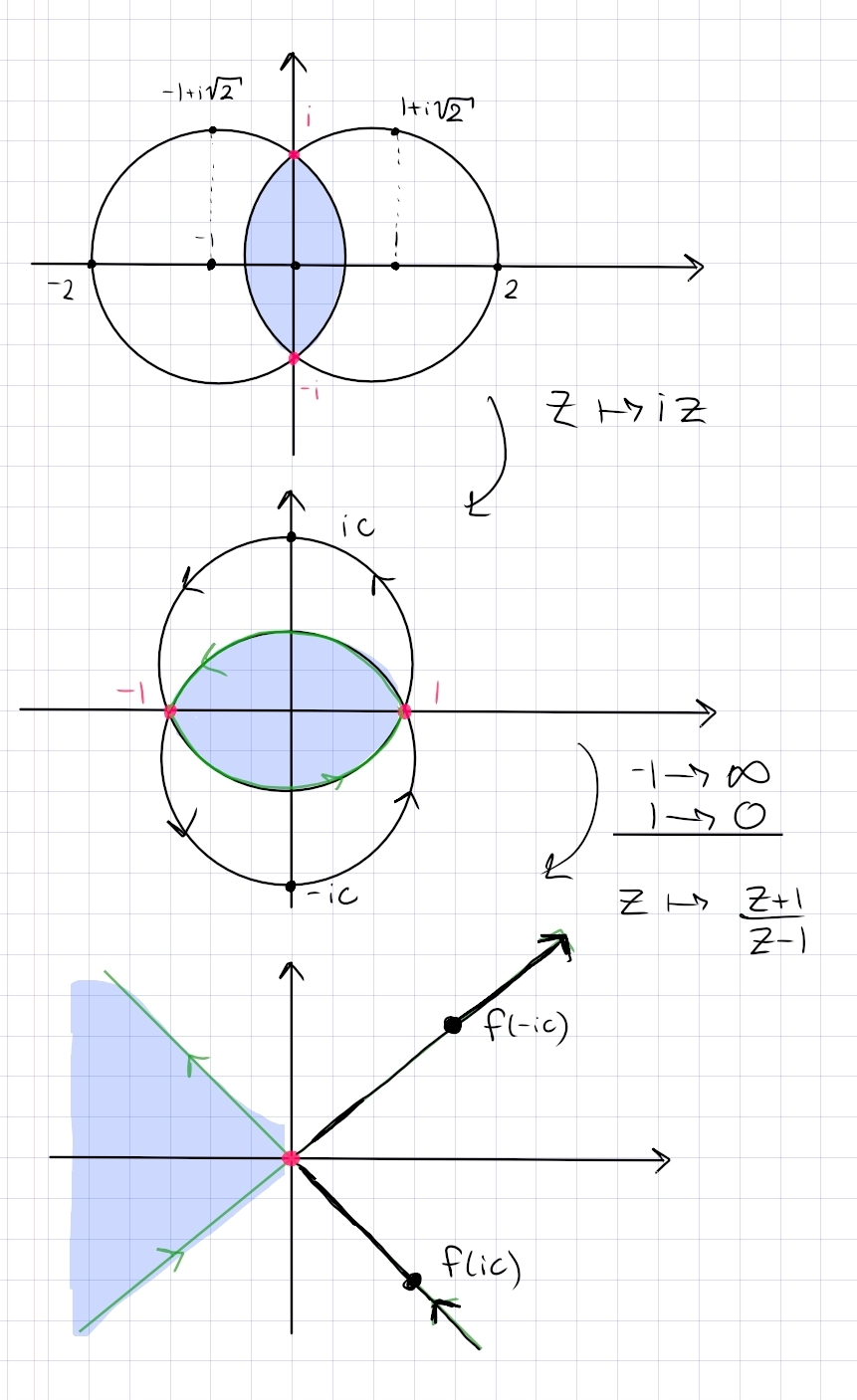
From here, it’s a standard exercise, so to sum up:
- Rotate \(R\to \tilde R\) by \(z\mapsto iz\) to get a horizontal lune with intersection points \(\pm 1\).
- Send \(-1\to \infty, 1\to 0\) by \(z\mapsto {z+1\over z-1}\) to send \(\tilde R \to 3\pi/4 < \operatorname{Arg}(z) < 5\pi/4\).
- Reflect by \(z\mapsto -z\) to get \(-\pi/4 < \operatorname{Arg}(z) < \pi/4\).
- “Open” by \(z\mapsto z^{\pi \over 2 \theta_0}\) to map to \(-\pi/2<\operatorname{Arg}(z) < \pi/2\), where here \(\theta_0 \coloneqq{\pi \over 4}\).
- Rotate by \(z\mapsto iz\) to get \(0 < \operatorname{Arg}(z) < {\pi \over 2}\), i.e. \({\mathbb{H}}\).
- Use the Cayley map \(z\mapsto {z-i\over z+i}\) to send \({\mathbb{H}}\to {\mathbb{D}}\).
Spring 2020.5, Spring 2019.6
^0df993
Find a conformal map that maps the region \begin{align*} R = \left\{{z {~\mathrel{\Big\vert}~}\Re(z) > 0,\, {\left\lvert {z - {1\over 2} } \right\rvert}> {1\over 2} }\right\} \end{align*} to the upper half plane.
Find a conformal map from \begin{align*} \left\{{ z{~\mathrel{\Big\vert}~}{\left\lvert {z -1 / 2} \right\rvert} >1 / 2, \Re(z)>0 }\right\} \end{align*} to \(\mathbb{H}\).
The main step: blow up the tangency.
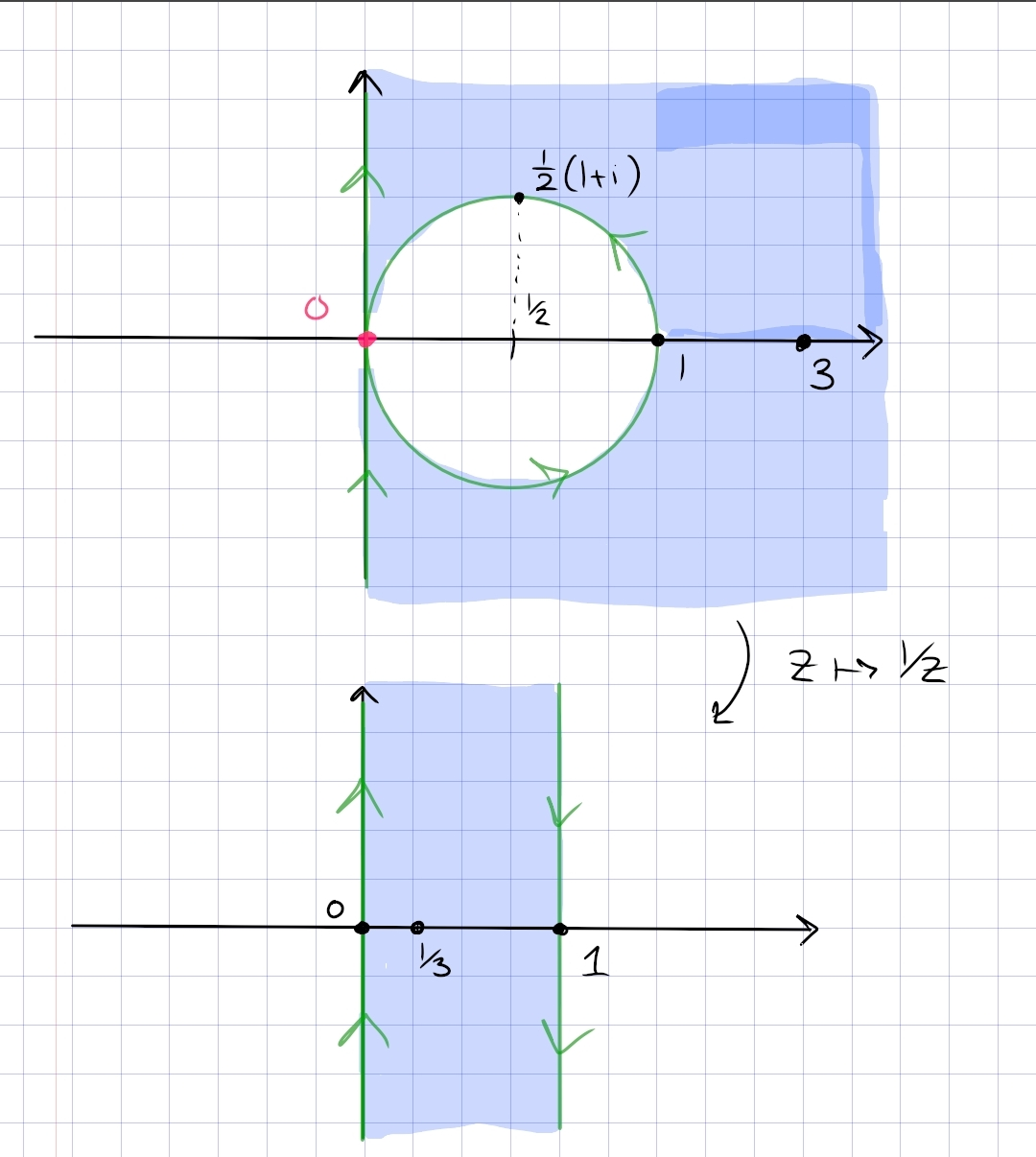
The individual maps:
- Send \(0\to \infty\) by \(z\mapsto {1\over z}\) to map \(R\) to \(0<\Re(z)<1\)
- Rotate with \(z\mapsto iz\) to map this to \(0< \Im(z) < 1\)
- Dilate by \(z\mapsto \pi z\) to get \(0 < \Im(z) < \pi\)
- Apply \(z\mapsto e^z\) to map to \({\mathbb{H}}\).
That steps 1 and 2 work requires a bit of analysis. Use that \(f(z) \coloneqq 1/z\) satisfies \(f({\mathbb{R}}) = {\mathbb{R}}\) and \(f(i{\mathbb{R}}) = i {\mathbb{R}}\). To see where the circle \(C_1\) gets mapped to, parameterize it as \begin{align*} \gamma(t) \coloneqq\left\{{{1\over 2}\qty{1+e^{it}} {~\mathrel{\Big\vert}~}t\in [-\pi, \pi]}\right\} .\end{align*}
Now computing its image: \begin{align*} f(\gamma(t)) &= {2 \over 1 + e^{it}} \\ &= {2e^{-it\over 2} \over e^{-it\over 2}(1 + e^{it})} \\ &= {2e^{-it} \over e^{-it\over 2} + e^{it\over 2} } \\ &= { 2e^{-it\over 2} \over 2\cos\qty{t\over 2} } \\ &= \sec\qty{t\over 2}\qty{\cos\qty{-t\over 2} + i\sin\qty{-t\over 2}} \\ &= \sec\qty{t\over 2}\qty{\cos\qty{t\over 2} - i\sin\qty{t\over 2}} \\ &= 1 - i\tan\qty{t\over 2} ,\end{align*} and as \(t\) runs from \(-\pi\) to \(\pi\), \(-\tan\qty{t\over 2}\) runs from \(+\infty\) to \(-\infty\). So this is a line along \(z=1\), oriented top to bottom as in the image.
Similarly, computing \(f(i{\mathbb{R}})\): parameterize \(\gamma(t) = it\) with \(t\in (-\infty, \infty)\), then \begin{align*} f(\gamma(t)) = {1\over it} = -{i\over t} ,\end{align*} and as \(t\) runs from \(0\) to \(\infty\), \(-1/t\) runs from \(-\infty\) to \(0\), and as \(t\) runs from \(-\infty\) to \(0\), \(-1/t\) runs from \(0\) to \(\infty\). So \(f(i{\mathbb{R}})\) is oriented from bottom to top, as in the image.
That the region outside the disc is mapped to the strip shown: points \(x\in {\mathbb{R}}\) with \({\left\lvert {x} \right\rvert} > 1\) map to \({\left\lvert {x} \right\rvert}<1\), which is in the strip. One can also conclude this by handedness: the original region is on the right with respect to \(C_1\) and also on the right with respect to \(i{\mathbb{R}}\), so the new region should be on the right with respect to both \(f(i{\mathbb{R}})\) and \(f(C_1)\) with their induced orientations.
UMN Spring 2009
Find a conformal map from the region bounded by \({\left\lvert {z - {i\over 2}} \right\rvert} = {1\over 2}\) and \({\left\lvert {z-i} \right\rvert} = 1\) to \({\mathbb{D}}\).
This is a lune with a single intersection vertex at \(z=i\). Orient the circles positively.
-
Take \(f(z) = {z+i\over z-i}\) to send
- \(i\to \infty\)
- \(-i\to 0\)
- \(1\to {1+i\over 1-i} = i\)
- \(0\to -1\)
So \({\left\lvert {z} \right\rvert} = 1\) is sent to the imaginary axis \(\left\{{it}\right\}\) for \(t\in (-\infty, \infty)\) oriented positively and \({\left\lvert {z- {i\over 2}} \right\rvert} = {1\over 2}\) is sent to \(\left\{{-1 + it}\right\}\) also oriented positively. The region then maps to \(-1 < \Re(z) < 0\).
-
Rotate by \(z\mapsto -i\pi z\) to get \(0 < \Im(z) < \pi\).
-
Take \(z\mapsto e^z\) to get \({\mathbb{H}}\).
-
Take \(z\mapsto {z-i\over z+i}\) to get \({\mathbb{D}}\).
Joukowski Maps, Blaschke Factors, Slits
Spring 2021.7 (Slit)
^644ace
Let \(R\) be the intersection of the right half-plane and the outside of the circle \({\left\lvert {z - {1\over 2}} \right\rvert} = {1\over 2}\) with the line segment \([1, 2]\) removed, i.e. \begin{align*} R = \left\{{z\in {\mathbb{C}}{~\mathrel{\Big\vert}~}\Re(z) > 0,\,\, {\left\lvert {z-{1\over 2}} \right\rvert} > {1\over 2} }\right\} \setminus\left\{{z \coloneqq x+iy {~\mathrel{\Big\vert}~}1\leq x\leq 2,\,\, y=0}\right\} .\end{align*} Find a conformal map from \(R\) to \({\mathbb{H}}\) the upper half-plane.
- Blow up the point of tangency: inverting through a circle sends inner circles to lines, fixes the real line, and preserves regions between curves. E.g. the image of \({\left\lvert {z-i/2} \right\rvert} =2\) is \(\left\{{ \Im(z) = 2}\right\}\)

- So \(z\to 1/z\) maps the region into a half-strip.
Note: this seems unusually difficult for a UGA question! This is a bigon with one vertex \(z_2 = 0\), so send it to infinity and keep track of the slit.
In steps:
- Use \(z\mapsto 1/z\) to get a vertical strip \(0<\Re(z) < 1\), where the slit maps to \([1/2, 1]\).
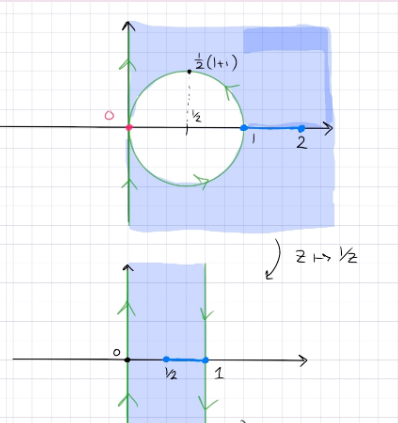
- Shift and dilate with \(z\mapsto \pi(z-1/2)\) to get \(-\pi/2<\Re(z) < \pi/2\), where the slit is now at \([0, \pi/2]\).
- Apply \(z\mapsto \sin(z)\) to get \({\mathbb{C}}\setminus[0, 1]\).
- Move the slit with \(z\mapsto 4(z-1/2)\) to get \({\mathbb{C}}\setminus[-2, 2]\).
- Apply \(z\mapsto z+z^{-1}\) to get \({\mathbb{C}}\setminus{\mathbb{D}}\), where the slit is now eliminated.
- Use \(z\mapsto 1/z\) to get \({\mathbb{D}}\)
- Use the inverse Cayley map \(z\mapsto i{1-z\over 1+z}\) to get \({\mathbb{H}}\).
Exercises (Lune)
Let \(\lambda = {1\over 2}\qty{1 + i \sqrt{3}}\) and find a map \begin{align*} R \coloneqq\left\{{{\left\lvert {z - \lambda} \right\rvert} < 1}\right\} \cap\left\{{{\left\lvert {z-\mkern 1.5mu\overline{\mkern-1.5mu\lambda\mkern-1.5mu}\mkern 1.5mu} \right\rvert} < 1 }\right\} \longrightarrow{\mathbb{D}} .\end{align*}
The region looks like the following:
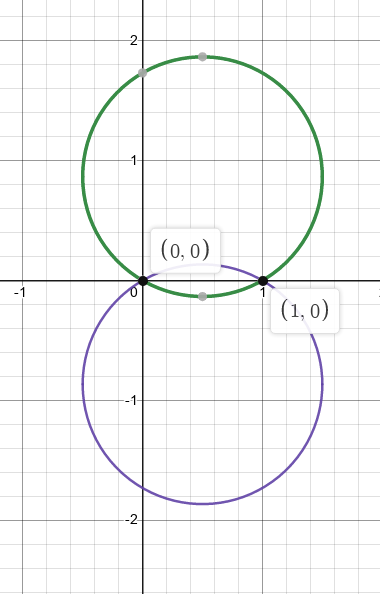
Following the general strategy for lunar regions, send the intersection points to \(0\) and \(\infty\) to get triangular sector. So choose to send \(0\to 0\) and \(1\to \infty\) by taking \begin{align*} f(z) \coloneqq{z\over z-1} .\end{align*}
Note: mistake here, really we need to compose with \(z\mapsto -z\) to get the picture, so take \(f(z) \coloneqq{z\over 1-z}\) instead!!
\begin{align*} f(R) = \left\{{z{~\mathrel{\Big\vert}~}-\theta_0 < \operatorname{Arg}(z) < \theta_0 }\right\},\qquad \theta_0 \coloneqq{\pi \over 6} .\end{align*}
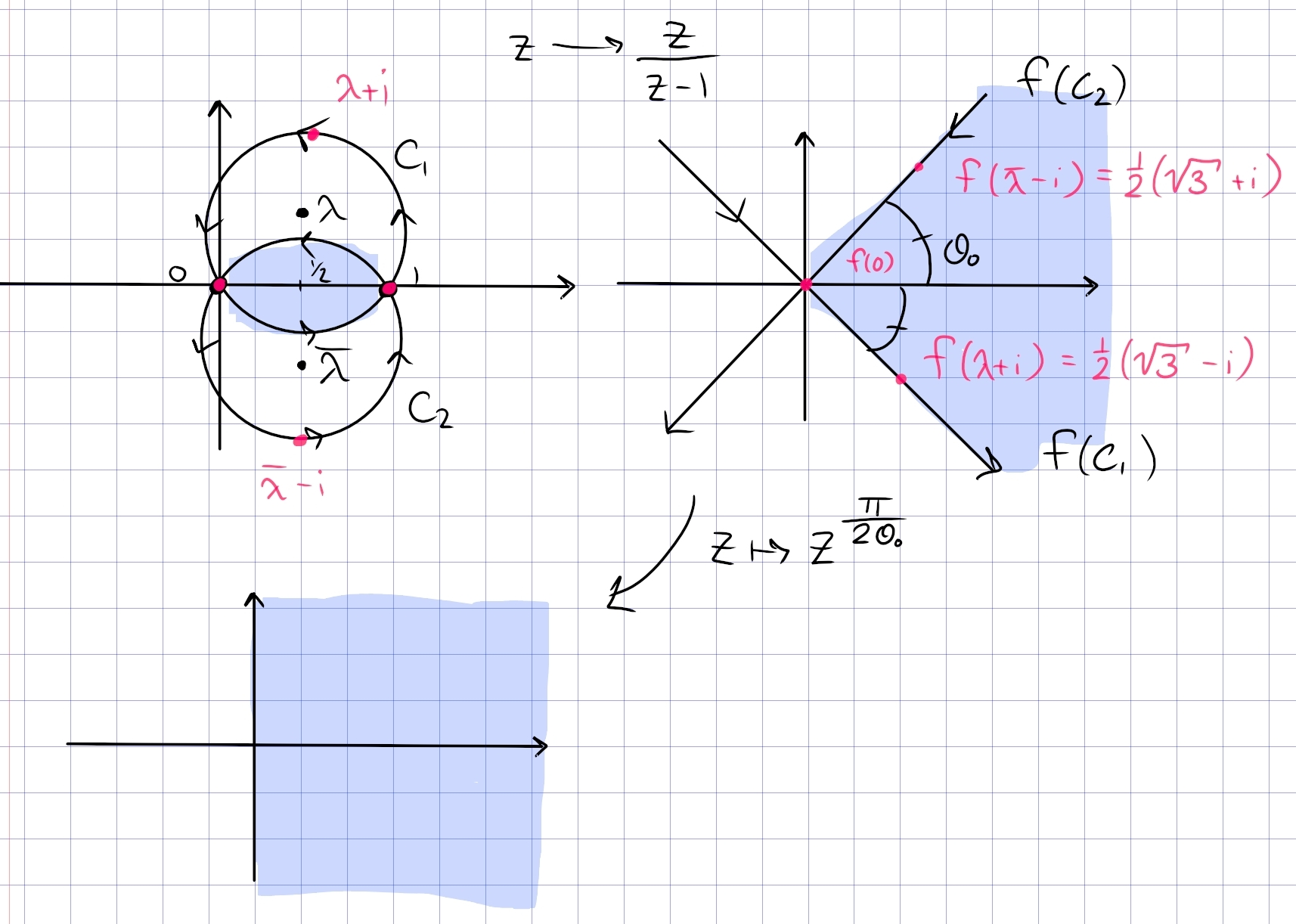
From here it is easy to map to the disc:
- \(z\mapsto {z\over z-1}\) sends \(R\) to \({\left\lvert {\operatorname{Arg}(z)} \right\rvert} < \theta_0\)
- \(z\mapsto z^{\pi \over 2\theta_0}\) maps \({\left\lvert {\operatorname{Arg}(z)} \right\rvert}<\theta_0 \to {\left\lvert {\operatorname{Arg}(z)} \right\rvert} < {\pi \over 2}\), the right half-plane.
- \(z\mapsto iz\) rotates the right half-plane into \({\mathbb{H}}\).
- \(z\mapsto {z-i\over z+i}\) maps \({\mathbb{H}}\to {\mathbb{D}}\).
Since both \(C_1, C_2\) pass through \(0, 1\), their images become circles passing through \(f(0)=0, f(1) = \infty\), so lines through the origin. Since \(f\) fixes \({\mathbb{R}}\) and the original region is symmetric about \({\mathbb{R}}\), the resulting region will also be symmetric about \({\mathbb{R}}\). As shown in the picture, since the interior of the region is to the left of each circle, the image will be to the left of each line. So it suffices to find the orientation of the two lines, as well as the angle that one of them makes with the \(x{\hbox{-}}\)axis.
Consider \(f(C_1)\) – it suffices to find \(\operatorname{Arg}(f(z_0))\) for any \(z_0\in C_1\), so look for a point (other than \(0, 1\)) where \(\operatorname{Arg}(f(z_0))\) is easy to compute. Noting that \(C_1\) intersects \(i{\mathbb{R}}\), we can find this point: \begin{align*} C_1: \qty{ x-{1\over 2}}^2 + \qty{y - {\sqrt 3 \over 2}}^2 &= 1 \\ x=0 \implies y = \pm{1\over 2} \sqrt{3} + {1\over 2} \sqrt{3} = 0, \sqrt{3} ,\end{align*} so choose \(z_0 = i\sqrt{3}\): \begin{align*} f(z_0) = {i\sqrt 3 \over i\sqrt 3 - 1} = {1\over 4}\qty{3-i\sqrt 3} \implies \operatorname{Arg}(f(z_0)) = {-\pi \over 6} .\end{align*} So \(C_1\) does get mapped to the line in the image running from \(Q_2\to Q_4\).
To get the orientation of \(C_1\), use that \(i\sqrt{3}, 0, 1\) map to \(f(z_0), 0, \infty\), which gives a \(Q_4\to Q_2\) orientation – oops.
Mistake here: should have chosen \(z\mapsto {z\over 1-z}\) to make the picture accurate!
Similarly for \(C_2\), setting \(z_1 \coloneqq-i\sqrt 3\) yields \(f(z_1) = {1\over 4}\qty{3+i\sqrt{3}}\), so \(\operatorname{Arg}(f(z_1)) = {\pi \over 6}\). The orientation is found from \(1,0,z_0 \mapsto \infty, 0, f(z_0)\), which is \(Q_3\to Q_1\).
Again, mistake in the picture!
Intersecting the regions that are to the left of each image curve yields \(5\pi/6 < \operatorname{Arg}(z) < 7\pi/6\), and composing with \(z\mapsto -z\) yields \(-\pi/6 < \operatorname{Arg}(z) < \pi/6\).
Fall 2020.5, Spring 2019.6 (Joukowski)
^931c0a
Consider the function \(f(z)=\frac{1}{2}\left(z+\frac{1}{z}\right)\) for \(z \in \mathbb{C} \backslash\{0\}\). Let \(\mathbb{D}\) denote the open unit disc.
-
Show that \(f\) is one-to-one on the punctured disc \(\mathbb{D} \backslash\{0\}\). What is the image of the circle \(|z|=r\) under this map when \(0<r<1\) ?
-
Show that \(f\) is one-to-one on the domain \(\mathbb{C} \backslash \mathbb{D}\). What is the image of this domain under this map?
- Show that there exists a map \(g: \mathbb{C} \backslash[-1,1] \rightarrow \mathbb{D} \backslash\{0\}\) such that \((g \circ f)(z)=z\) for all \(z \in \mathbb{D} \backslash\{0\}\). Describe the map \(g\) by an explicit formula.
Part a: That \(f: {\mathbb{C}}\setminus\left\{{0}\right\}\to {\mathbb{D}}\setminus\left\{{0}\right\}\) is injective: compute the derivative as \begin{align*} f'(z) = {1\over 2}\qty{1 - {1\over z^2}} ,\end{align*} which only vanishes at \(z=\pm 1\). Away from 0 in \({\mathbb{D}}\), \(f'\) is nonzero and continuous, so by the inverse function theorem \(f\) is a local homeomorphism onto its image, and in particular is injective.
The images of circles: parameterize one as \(\gamma(t) = Re^{it}\) for \(t\in [-\pi, \pi]\). Note that if \(R=1\), \(f(\gamma(t)) = {1\over 2}\qty{e^{it} + e^{-it}} = \cos(t)\), so as \(t\) increases from \(-\pi\to \pi\), the interval \([-1, 1]\) is covered twice. For \(0<R<1\), \begin{align*} f(\gamma(t)) &= {1\over 2}\qty{ Re^{it} + {1\over Re^{it}}} \\ &= {1\over 2}\qty{Re^{it} + R^{-1}e^{-it} } \\ &= {1\over 2}\qty{R\cos(t) + iR\sin(t) + R^{-1}\cos(-t) + iR^{-1}\sin(-t) } \\ &= {1\over 2}\qty{R\cos(t) + iR\sin(t) + R^{-1}\cos(t) - iR^{-1}\sin(-t) } \\ &= {1\over 2}\qty{R+R^{-1}}\cos(t) + i{1\over 2}\qty{R-R^{-1}}\sin(t) \\ &\coloneqq H_R \cos(t) + iV_R\sin(t) ,\end{align*} which is generally the equation of an ellipse of horizontal radius \(H_R\) and vertical radius \(V_R\). As \(R\) varies, these sweep out ellipses of vertical radii from 0 to \(\infty\). One can compute the foci: their distance from \(z=0\) is given by \(c\), where \begin{align*} c^2 = H_R^2 - V_R^2 = {1\over 4}(R+R^{-1})^2 - {1\over 4}(R-R^{-1})^2 = 1 ,\end{align*} so the foci are all at \(\pm 1\in {\mathbb{R}}\). One can check that these are clockwise when \(0<R<1\) and counterclockwise when \(R>1\).
In general, you take the coefficient for the major axis squared minus that of the minor axis squared. The foci are along the major axis.
Part b: The claim is that \(f({\mathbb{C}}\setminus{\mathbb{D}}) = {\mathbb{C}}\setminus[-1, 1]\).
Note that \(f(z) = f(1/z)\), so for \(z\neq 1/z\) there are exactly two preimages. These points are exactly \(z=\pm 1\), so we need to take the domain \(\Omega \coloneqq{\mathbb{C}}\setminus({\mathbb{D}}\cup\left\{{\pm 1}\right\})\) to get injectivity. Otherwise, for every \(z\in \Omega\), exactly one of \(z\) or \(1/z\) is in \({\mathbb{D}}\), so \(f(z)\) takes on unique values in \(\Omega\). By part 1, the images of circles of radius \(R\) are ellipses, and these sweep out the entire plane outside of \([-1, 1]\):

To be explicit, one can just solve for the two preimages. Setting \(w=f(z)\) and solving for \(z\) yields \begin{align*} w &= {1\over 2}\qty{z + {1\over z}} \\ \implies 2wz &= z^2 + 1 \\ \implies z^2 - 2wz + 1 &= 0 \\ \implies z &= {2w \pm \sqrt{4w^2 -4} \over 2} \\ \implies z &= w\pm \sqrt{w^2-1} ,\end{align*} where in order to define \(\sqrt{w^2-1}\), one needs a branch cut for \(\operatorname{Log}\) along \([-1, 1]\), which is precisely what we’re deleting from the image.
Part c: as in a usual conformal map problem, find a map to \({\mathbb{C}}\setminus[-1,1]\to {\mathbb{D}}\).
-
Send \(-1\to 0\) and \(1\to \infty\) with \(z\mapsto {z+1\over z-1}\). Checking that \(f(0) = -1\), this yields \({\mathbb{C}}\setminus{\mathbb{R}}_{\leq 0}\).
-
Unwrap with \(z\mapsto \sqrt{z}\) to obtain the right half-plane \(-\pi/2<\operatorname{Arg}(z) < \pi/2\).
-
Apply the rotated Cayley map \(z\mapsto {z-1\over z+1}\) to map this to \({\mathbb{D}}\).
This composes to \begin{align*} g(z) &= {\sqrt{z+1\over z-1} -1 \over \sqrt{z+1\over z-1} +1} \\ &= { \qty{ \sqrt{z+1} - \sqrt{z-1}}^2 \over (z+1)-(z-1) } \\ &= z - \sqrt{z^2-1} ,\end{align*} and checking that it has the right inverse: \begin{align*} w &= z-\sqrt{z^2-1} \\ \implies (z-w)^2 &= z^2-1 \\ \implies w^2+1 &= 2wz \\ \implies z = {1\over 2}\qty{w + {1\over w}} .\end{align*}
Tie’s Extra Questions: Spring 2015 (Joukowski)
Prove that \(\displaystyle{f(z)=-\frac{1}{2}\left(z+\frac{1}{z}\right)}\) is a conformal map from the half disc \begin{align*} \{z=x+iy:\ |z|<1,\ y>0\} \end{align*} to \({\mathbb{H}}\coloneqq\{z=x+iy:\ y>0\}\).
Consider the images of arcs \(\gamma_R(t) \coloneqq Re^{it}\) for \(t\in [0, \pi]\) and \(0<R<1\), which fill out the upper half disc: \begin{align*} f(Re^{it}) = - {1\over 2}\qty{ \qty{R+R^{-1}}\cos(t) + i(R-R^{-1})\sin(t) } \coloneqq H_R\cos(t) + V_R\sin(t) ,\end{align*} where \(H_R \coloneqq-{1\over 2}{R+R^{-1}}\) and \(V_R \coloneqq-{1\over 2}(R-R^{-1})\). Note that \(H_R\in (-\infty, -1]\) and \(V_R \in (0, \infty)\) – in particular, since \(V_R>0\), as \(t\) ranges through \((0, \pi)\), this traces out the top half of an ellipse (noting that \(V_R<0\) would trace out the bottom).
As \(R\) ranges from \((0, 1)\), \(V_R\) ranges from \((0, \infty)\), so this traces out all such elliptic arcs in \({\mathbb{H}}\) passing through \(H_R <0, iV_R \in {\mathbb{H}}, -H_R>0\). So these trace out all of \({\mathbb{H}}\).
UMN Spring 2008
Define \(A \coloneqq\left\{{\Re(z) > 0, \Im(z) > 0}\right\}\). Find a conformal equivalence \(\Delta \cap A \to A\).
In steps:
- Unfold with \(z\mapsto z^2\) to get \({\mathbb{D}}\cap{\mathbb{H}}\).
- Joukowski it with \(z\mapsto -{1\over 2}(z+z^{-1})\) to get \({\mathbb{H}}\).
- Fold with \(z\mapsto z^{1\over 2}\) to get \(Q_1 = A\).
Linear Fractional Transformations
Tie’s Extra Questions: Spring 2015
Let \(C\) and \(C'\) be two circles and let \(z_1 \in C\), \(z_2 \notin C\), \(z'_1 \in C'\), \(z'_2 \notin C'\). Show that there is a unique fractional linear transformation \(f\) with \(f(C) = C'\) and \(f(z_1) = z'_1\), \(f(z_2) = z'_2\).
Main idea: both circles can be uniformized in ways that send \(z_2, z_2'\) to zero. Handling \(C\):
- \(f_1\): Uniformize by translating and scaling \(C\) to \(S^1\). Note that the image of \(z_1\) is in \(S^1\)
- \(f_2\): if \(z_2\) was not enclosed by \(C\), apply \(z\mapsto 1/z\) to move \(z_2\) into \({\mathbb{D}}\). Otherwise just take \(f_2 = \operatorname{id}\). In either case, \(z_1\in S^1\) is preserved.
- \(f_3\): apply a Blaschke factor \(\psi_a(z)\) to move \(z_2\to 0\) in \({\mathbb{D}}\). Since \(\psi_a\) preserves \(S^1\), \(z_1\) is moved to another point in \(S^1\).
Define \(F\coloneqq f_3 \circ f_2 \circ f_1\). Similarly define \(g_1,\cdots, g_3\) and \(G\) for \(C'\), so \(z_2'\to 0\) in \({\mathbb{D}}\). Now \(F(z_1), G(z_1')\in S^1\), so there is a rotation \(h: z\mapsto \lambda z\) that sends \(F(z_1)\to G(z_1')\).
Take the final map to be \(f\coloneqq G\circ h \circ F^{-1}\).
UMN Fall 2012
Suppose \(f\) is holomorphic on \(\Delta^*\) and \(\Re(f) \geq 0\). Show that \(f\) has a removable singularity at \(z=0\).
We have \(f: \Delta^* \to \left\{{\Re(z) > 0}\right\}\), so let \(T: \left\{{\Re(z) > 0}\right\}\to \Delta\) be the rotated Cayley map \(T(z) = {z-1\over z+1}\). Then \(G\coloneqq T^{-1}\circ f: \Delta^* \to \Delta\), and since \({\left\lvert {T} \right\rvert} < 1\), \(z=0\) is a removable singularity for \(F\) and \(F\) extends holomorphically to \(G:\Delta\to {\mathbb{C}}\), since a priori \(G(0)\) may not be bounded by 1. Supposing \(G\) is not constant, \(G(\Delta) \subseteq \bar{\Delta)\) by continuity and \(G(\Delta)\) is open by the open mapping theorem, and \(\Delta = f(\Delta) \subseteq G(\Delta)\), so \(G:\Delta\to \Delta\) is a map of the disc. Then \(F \coloneqq T\circ G: \Delta\to \left\{{\Re(z) > 0}\right\}\) is an extension of \(F\) which is bounded in neighborhoods of \(z=0\), making zero a removable singularity for \(f\).
UMN Fall 2009
Suppose \(f\) is entire and \(f({\mathbb{C}}) \subseteq {\mathbb{H}}\). Show that \(f\) must be constant.
Write \(T:{\mathbb{C}}\to {\mathbb{D}}\) for the Cayley map, then \(F\coloneqq f\circ T\) satisfies \(F({\mathbb{C}}) = T(f({\mathbb{C}})) \subseteq T({\mathbb{H}}) = {\mathbb{D}}\), so \(F\) is a bounded entire function and thus constant. So \(c = F(z) = T(f(z)) \implies f(z) = T^{-1}(c)\), making \(f\) constant.
Schwarz Lemma
Fall 2020.4 (Schwarz double root) #stuck
^0f90ac
Let \(\mathbb{D}:=\{z:|z|<1\}\) denote the open unit disk. Suppose that \(f(z): \mathbb{D} \rightarrow \mathbb{D}\) is holomorphic, and that there exists \(a \in \mathbb{D} \backslash\{0\}\) such that \(f(a)=f(-a)=0\).
-
Prove that \(|f(0)| \leq|a|^{2}\).
-
What can you conclude when \(|f(0)|=|a|^{2} ?\)
Part 1:
Write \(\psi_a(z) \coloneqq{a-z\over 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu z}\) for the Blaschke factor of \(a\), and define \begin{align*} g(z) \coloneqq{f(z) \over \psi_a(z) \psi_{-a}(z)} .\end{align*}
\({\left\lvert {g(z)} \right\rvert}\leq 1\) on \({\mathbb{D}}\).
\({\left\lvert {\psi_a(z)} \right\rvert} = 1\) on \({{\partial}}{\mathbb{D}}\), so \(\lim_{r\to 1}\psi_a(re^{it}) = 1\) for any fixed \(t\). Then for any \(f\) with \({\left\lvert {f} \right\rvert} \leq 1\) in \({\mathbb{D}}\), \begin{align*} {\left\lvert {f(re^{it} ) \over \psi_a(re^{it} ) } \right\rvert} \leq {1\over \psi_a(re^{it})} \leq {1\over \sup_{t} \psi_a(re^{it}) } \overset{r\to 1}\longrightarrow 1 .\end{align*} So apply this to \(f=g\) and \(f={g\over \psi_a}\) to get it for \({f\over \psi_a \psi_{-a}}.\)
In particular, \({\left\lvert {g(0)} \right\rvert} \leq 1\), so \begin{align*} 1\geq {\left\lvert {g(0)} \right\rvert} = {{\left\lvert {f(0)} \right\rvert} \over {\left\lvert {B_a(0)} \right\rvert} \cdot {\left\lvert {B_{-a}(0)} \right\rvert}} = {{\left\lvert {f(0)} \right\rvert} \over {\left\lvert {a} \right\rvert}^2} \implies {\left\lvert {a} \right\rvert}^2 \geq {\left\lvert {f(0)} \right\rvert} .\end{align*}
Part 2: Applying Schwarz-Pick: \begin{align*} {\left\lvert {f'(0)} \right\rvert} \leq {1 - {\left\lvert {f(0)} \right\rvert}^2 \over 1 - {\left\lvert {0} \right\rvert}^2 } = 1-{\left\lvert {a} \right\rvert}^2 < 1 ,\end{align*} using that \(a\neq 0\), so \(f\) is a contraction.
Can write \(f_e(z) \coloneqq{f(a) + f(-a) \over 2}\) to write \(f_e(z) = g(z^2)\). Compose with some \(\psi_a\) to get \(0\to 0\) and apply Schwarz – unclear how to unwind what happens in the case of equality though.
Fall 2021.5
^ee1748
Assume \(f\) is an entire function such that \(|f(z)|=1\) on \(|z|=1\). Prove that \(f(z)=e^{i \theta} z^{n}\), where \(\theta\) is a real number and \(n\) a non-negative integer.
Suggestion: First use the maximum and minimum modulus theorem to show \begin{align*} f(z)=e^{i \theta} \prod_{k=1}^{n} \frac{z-z_{k}}{1-\mkern 1.5mu\overline{\mkern-1.5muz_{k}\mkern-1.5mu}\mkern 1.5mu z} \end{align*} if \(f\) has zeros.
First show the hint: assume \(f\) has nonzero zeros. Write \(Z(f) \coloneqq f^{-1}(0)\) for the set of zeros in \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\).
If we assume \(f\) is continuous on \({\mathbb{D}}\), then \({\sharp}Z(f) < \infty\)
Suppose \({\sharp}Z(f) = \infty\), then by compactness of \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) there is a limit point \(z_0\). If \(z_0 \in {\mathbb{D}}\), then there is a sequence \(\left\{{z_k}\right\}\to z_0\) with \(f(z_k) = 0\) for every \(k\), so \(f\) is zero on a set \(S\coloneqq\left\{{z_k}\right\}_{k\geq 1} \cup\left\{{z_0}\right\}\) with an accumulation point and this forces \(f\equiv 0\) on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) by the identity principle, contradicting \({\left\lvert {f} \right\rvert} = 1\) on \({{\partial}}{\mathbb{D}}\)>
Otherwise, if \(z_0\in {{\partial}}{\mathbb{D}}\), using continuity of \(f\) we have \(f(z_k) = 0\) for all \(k\) and \(z_k\to z_0\) so \(f(z_0) = 0\), again contradiicting \({\left\lvert {f} \right\rvert} = 1\) on \({{\partial}}{\mathbb{D}}\).
So write \(Z(f) = \left\{{z_1,\cdots, z_m}\right\}\) and define \begin{align*} g(z) \coloneqq\prod_{1\leq k \leq m} {z-z_k \over 1 - \mkern 1.5mu\overline{\mkern-1.5muz_k\mkern-1.5mu}\mkern 1.5mu z}, \quad h(z) \coloneqq{f(z) \over g(z)} .\end{align*}
\(h(z) \equiv 1\) is constant on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\), so that \(f = \lambda g\) for some \(\lambda \in S^1\), i.e. \(\lambda = e^{i\theta}\) for some \(\theta\).
Note that \(h\) cancels all zeros of \(f\), so \(h\) is nonzero and holomorphic on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\). Moreover \({\left\lvert {g(z)} \right\rvert} \leq 1\) on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) since these are well-known to be in \(\mathop{\mathrm{Aut}}({\mathbb{D}})\). It’s also well-known that \({\left\lvert {g(z)} \right\rvert} = 1\) on \({{\partial}}{\mathbb{D}}\). Thus \({\left\lvert {h(z)} \right\rvert} = 1\) and \({\left\lvert {1\over h(z)} \right\rvert} =1\) on \({{\partial}}{\mathbb{D}}\), and by the maximum modulus principle, \begin{align*} {\left\lvert {h(z)} \right\rvert} \leq 1 \quad\text{ and }\quad {\left\lvert {1\over h(z)} \right\rvert}\leq 1 \quad \text{ on } {\mathbb{D}} ,\end{align*} forcing \({\left\lvert {h(z)} \right\rvert}\equiv 1\) and thus \(h(z) = e^{i\theta}\) for some \(\theta\).
So we now have \begin{align*} f(z) = e^{i\theta} \prod_{1\leq k\leq m} {z-z_k \over 1 -\mkern 1.5mu\overline{\mkern-1.5muz_k\mkern-1.5mu}\mkern 1.5mu z} ,\end{align*} which has poles at points \(z\) for which \(\mkern 1.5mu\overline{\mkern-1.5muz_k\mkern-1.5mu}\mkern 1.5muz=1\) for some \(z_k\in Z(f)\). However, since we assumed \(f\) was entire, it can have no such poles, which forces \(z_k = 0\) for all \(k\). But then \begin{align*} f(z) = e^{i\theta}\prod_{1\leq k \leq m}{z- 0 \over 1 - 0\cdot z} = e^{i\theta}z^m .\end{align*}
Fall 2021.6 (Schwarz manipulation)
^33ab95
Show that if \(f: D(0, R) \rightarrow \mathbb{C}\) is holomorphic, with \(|f(z)| \leq M\) for some \(M>0\), then \begin{align*} \left|\frac{f(z)-f(0)}{M^{2}-\overline{f(0)} f(z)}\right| \leq \frac{|z|}{M R} . \end{align*}
The strategy:
- Write the RHS as \(a\). Note that we need to get rid of the \(M^2\) on the LHS, so keep the \(M\) around and write \(a \coloneqq z/R\) so \(z = aR\).
-
Make the substitution to get
\begin{align*}
{\left\lvert {f(aR) - f(0) \over M^2 - \mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(aR) } \right\rvert} \leq M^{-1}{\left\lvert {a} \right\rvert} \\
\implies
{\left\lvert {M\qty{ f(aR) - f(0)} \over M^2 - \mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(aR) } \right\rvert} \leq {\left\lvert {a} \right\rvert} \\
{\left\lvert { f(aR)/M - f(0)/M \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(aR)/M^2 } \right\rvert} \leq {\left\lvert {a} \right\rvert}
.\end{align*}
- Recognize the LHS as \(\psi_w(g(a))\) for \(w\coloneqq f(0)/M\) and \(g(a) \coloneqq f(aR)/M\).
Proof due to Swaroop Hegde!
Fix \(R, M\) and make a clever choice: define \begin{align*} F: {\mathbb{D}}&\to {\mathbb{C}}\\ z &\mapsto {f(Rz) \over M} .\end{align*} Write \(a\coloneqq F(0)\) and consider the Blaschke factor \begin{align*} \psi_a(z) \coloneqq{a-z \over 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu z} \in \mathop{\mathrm{Aut}}({\mathbb{D}}) ,\end{align*} and define \begin{align*} g: {\mathbb{D}}&\to {\mathbb{D}}\\ z &\mapsto (\psi_a \circ F)(z) .\end{align*} Then \(g(0) = 0\) and \({\left\lvert {g(z)} \right\rvert} \leq 1\) for all \(z\in {\mathbb{D}}\), so by Schwarz we have \({\left\lvert {g(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}\) for all \(z\in {\mathbb{D}}\). Thus for all \(z\in {\mathbb{D}}\), \begin{align*} &{\left\lvert {g(z)} \right\rvert} \leq z \\ \\ \iff & {\left\lvert {\psi_a(F(z)) } \right\rvert} \leq {\left\lvert {z} \right\rvert} \\ \\ \iff & {\left\lvert { {f(Rz) \over M} - a \over 1 - {\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu f(Rz) \over M} } \right\rvert} \leq {\left\lvert {z} \right\rvert} \\ \\ \iff & {\left\lvert {f(Rz) - f(0) \over 1 - {\mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(Rz) \over M^2 } } \right\rvert} \leq {\left\lvert {z} \right\rvert} \\ \\ \iff & {\left\lvert {f(Rz) - f(0) \over M^2 - \mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(Rz) } \right\rvert} \leq {{\left\lvert {z} \right\rvert} \over M} \\ \\ \iff & {\left\lvert {f(w) - f(0) \over M^2 - \mkern 1.5mu\overline{\mkern-1.5muf(0)\mkern-1.5mu}\mkern 1.5mu f(w) } \right\rvert} \leq {{\left\lvert {w} \right\rvert} \over MR} ,\end{align*} which holds for all \(w\in {\mathbb{D}}\) by replacing \(Rz\) with \(w\) (i.e. to show this equality for arbitrary \(w\in {\mathbb{D}}\), write \(w = Rz\) for some \(z\in {\mathbb{D}}\) and run this chain of inequalities backward).
Scaling Schwarz
Let \(\mkern 1.5mu\overline{\mkern-1.5muB\mkern-1.5mu}\mkern 1.5mu(a, r)\) denote the closed disc of radius \(r\) about \(a\in {\mathbb{C}}\). Let \(f\) be holomorphic on an open set containing \(\mkern 1.5mu\overline{\mkern-1.5muB\mkern-1.5mu}\mkern 1.5mu(a, r)\) and let \begin{align*} M \coloneqq\sup_{z\in \mkern 1.5mu\overline{\mkern-1.5muB\mkern-1.5mu}\mkern 1.5mu(a, r)} {\left\lvert {f(z)} \right\rvert} .\end{align*}
Prove that \begin{align*} z\in \mkern 1.5mu\overline{\mkern-1.5muB\mkern-1.5mu}\mkern 1.5mu\qty{a, {r\over 2}},\,z\neq a, \qquad {{\left\lvert { f(z) - f(a)} \right\rvert} \over {\left\lvert {z-a} \right\rvert}} \leq {2M \over r} .\end{align*}
Set \begin{align*} g(z) \coloneqq{f(Rz+a) - f(a) \over 2M} ,\end{align*} so that \(g(0) = 0\) and \(g:{\mathbb{D}}\to {\mathbb{D}}\) so Schwarz applies, \begin{align*} {\left\lvert {g(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert} \implies {\left\lvert { f(Rz+a) - f(a) \over 2M } \right\rvert} &\leq {\left\lvert {z} \right\rvert} \\ \implies {\left\lvert { f(Rz+a) - f(a) } \right\rvert} &\leq 2M {\left\lvert {z} \right\rvert} \\ \implies {\left\lvert { f(w) - f(a) } \right\rvert} &\leq 2M{\left\lvert { w-a\over R} \right\rvert} \\ \implies {\left\lvert {f(w) - f(a) \over w-a} \right\rvert} &\leq {2M \over R} .\end{align*}
Bounding derivatives
Suppose \(f: {\mathbb{D}}\to {\mathbb{H}}\) is analytic and satisfies \(f(0) = 2\). Find a sharp upper bound for \({\left\lvert {f'(0)} \right\rvert}\), and prove it is sharp by example.
Some useful facts about the Cayley map:
- \(C(z) \coloneqq{z-i\over z+i}\) maps \({\mathbb{H}}\to {\mathbb{D}}\) sending \(i\to 0\).
- \(C^{-1}(z) \coloneqq-i {z+1\over z-1}\) maps \({\mathbb{D}}\to{\mathbb{H}}\) sending \(0\to i\).
- \(C'(z) = {2i\over (z+i)^2}\) and \(C'(i) = -{1\over 2}i\).
- \((C^{-1})'(z) = {2i\over (z-1)^2}\) and \(C'(0) = 2i\).
- A mistake that’s useful to know: \(\psi_w'(z) = {1-{\left\lvert {w} \right\rvert}^2 \over (1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5muz )^2}\) and \(\psi_w'(w) \to \infty\).
Define \(g:{\mathbb{H}}\to {\mathbb{H}}\) by \(g(z) = {1\over 2}iz\), so \(g(2) = i\). Then set \(F \coloneqq C\circ g \circ f: {\mathbb{D}}\to {\mathbb{D}}\) where \(C(z) \coloneqq{z-i\over z+i}\) is the Cayley map.Since \(F(0) = C(g(f(0))) = C(g(2)) = C(i) = 0\), Schwarz applies to \(F\) and \({\left\lvert {F'(z)} \right\rvert}\leq 1\) for \(z\in {\mathbb{D}}\). By the chain rule, \begin{align*} F'(z) = f'( (g\circ C) (z))\cdot g'(C(z)) \cdot C'(z) .\end{align*} Setting \(g(C(z)) = 0\) yields \(z=C^{-1}(g^{-1}(0)) = C^{-1}(0) = i\). \begin{align*} F'(i) &= f'(0) \cdot g'(0) \cdot C'(i) \\ \implies {\left\lvert {f'(0)} \right\rvert} &\leq {\left\lvert {F'(i) \over g'(0) C'(i)} \right\rvert} \\ &\leq {1\over {\left\lvert {g'(0)} \right\rvert} \cdot {\left\lvert {C'(i)} \right\rvert} } \\ &= {1\over {\left\lvert {i\over 2} \right\rvert} \cdot {\left\lvert {-{i\over 2} } \right\rvert} } \\ &= 4 .\end{align*}
By Schwarz, if \({\left\lvert {F'(z)} \right\rvert} = 1\) for any \(z\in {\mathbb{D}}\), we’ll have \(F(z) = \lambda z\) for some \({\left\lvert { \lambda} \right\rvert} = 1\). Unwinding this: \begin{align*} F(z) &= \lambda z \implies (C\circ g\circ f)(z) = \lambda z \\ \implies f(z) &= g^{-1}(C^{-1}(\lambda z)) = g^{-1}\qty{-i {\lambda z + 1 \over \lambda z - 1}} \\ \implies f(z) &= -2 {\lambda z + 1\over \lambda z - 1} .\end{align*} Moreover \(f'(z) = -2\qty{-2\lambda \over (\lambda z - 1)^2}\), so \begin{align*} {\left\lvert {f'(0)} \right\rvert} = 4{\left\lvert {\lambda} \right\rvert} = 4 .\end{align*}
Schwarz for higher order zeros
Suppose \(f:{\mathbb{D}}\to{\mathbb{D}}\) is analytic, has a single zero of order \(k\) at \(z=0\), and satisfies \(\lim_{{\left\lvert {z} \right\rvert} \to 1} {\left\lvert {f(z)} \right\rvert} = 1\). Give with proof a formula for \(f(z)\).
Note \({\left\lvert {f(z)} \right\rvert}\leq 1\), and \(g\coloneqq f(z)/z^k\) has a removable singularity at zero since \(g\) is bounded on \({\mathbb{D}}\): fixing \({\left\lvert {z} \right\rvert} = r < 1\), \begin{align*} {\left\lvert {g(z)} \right\rvert} = {\left\lvert {f(z)\over z^k} \right\rvert} = {\left\lvert {f(z)} \right\rvert}r^{-k}\leq r^{-k}\overset{r\to 1}\longrightarrow 1 .\end{align*} So \(g:{\mathbb{D}}\to {\mathbb{D}}\) since \({\left\lvert {g(z)} \right\rvert}\leq 1\) on \({\mathbb{D}}\) by the MMP. Since \(g\) has no zeros on \({\mathbb{D}}\), by the MMP \({\left\lvert {g} \right\rvert} \geq 1\) on \({\mathbb{D}}\), so \({\left\lvert {g} \right\rvert} = 1\) is constant, making \(g(z) = \lambda z\) a rotation. Then \(f(z) = \lambda z^n\).
Alternative to MMP: if \(g\) has no zeros in \({\mathbb{D}}\), \(g\) admits a conjugate reflection through \({\mathbb{D}}\) by \(z\mapsto 1/\mkern 1.5mu\overline{\mkern-1.5muf(1/\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu\). This is bounded and entire, thus constant, making \(g\) constant.
Schwarz with an injective function
Suppose \(f, g: {\mathbb{D}}\to \Omega\) are holomorphic with \(f\) injective and \(f(0) = g(0)\).
Show that \begin{align*} \mathop{\mathrm{\forall}}0 < r < 1,\qquad g\qty{\left\{{{\left\lvert {z} \right\rvert} < r}\right\}} \subseteq f\qty{\left\{{{\left\lvert {z} \right\rvert} < r}\right\}} .\end{align*}
The first part of this problem asks for a statement of the Schwarz lemma.
Since \(f\) is injective, it has a left-inverse \(f^{-1}\), and \(F\coloneqq f^{-1}g\) is well-defined. Since \(F:{\mathbb{D}}\to {\mathbb{D}}\) and \(F(0) = 0\), Schwarz applies and \({\left\lvert {F(z)} \right\rvert} \leq z\) on \({\mathbb{D}}\). Unwinding: \begin{align*} {\left\lvert {(f^{-1}\circ g)(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert} \implies {\left\lvert {g(z)} \right\rvert} \leq {\left\lvert {f(z)} \right\rvert} \qquad \forall {\mathbb{D}}\in {\mathbb{Z}} .\end{align*} This says that \(g({\mathbb{D}}) \subseteq f({\mathbb{D}})\), and in particular this holds on all \({\mathbb{D}}_r(0)\), so \(g({\mathbb{D}}_r(0)) \subseteq f({\mathbb{D}}_r(0))\).
Reflection principle
Let \(S\coloneqq\left\{{z\in {\mathbb{D}}{~\mathrel{\Big\vert}~}\Im(z) \geq 0}\right\}\). Suppose \(f:S\to {\mathbb{C}}\) is continuous on \(S\), real on \(S\cap{\mathbb{R}}\), and holomorphic on \(S^\circ\).
Prove that \(f\) is the restriction of a holomorphic function on \({\mathbb{D}}\).
Define a function \begin{align*} F(z) \coloneqq \begin{cases} f(z) & \Im(z)\geq 0 \\ \mkern 1.5mu\overline{\mkern-1.5muf(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu & \Im(z) < 0 \end{cases} .\end{align*} Then \(F\) is holomorphic on \(\tilde S\coloneqq\left\{{z\in {\mathbb{D}}{~\mathrel{\Big\vert}~}\Im(z) < 0}\right\}\) – write \(w_0\in \tilde S\) as \(w_0 = \mkern 1.5mu\overline{\mkern-1.5muz_0\mkern-1.5mu}\mkern 1.5mu\) for some \(z_0\in S\), then \begin{align*} f(z) &= \sum_{k\geq 0}c_k (z-z_0)^k \\ \implies \mkern 1.5mu\overline{\mkern-1.5muf(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu &= \sum_{k\geq 0}\mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu \mkern 1.5mu\overline{\mkern-1.5mu\qty{\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu - z_0}^k\mkern-1.5mu}\mkern 1.5mu \\ &= \sum_{k\geq 0}\mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu \qty{z - \mkern 1.5mu\overline{\mkern-1.5muz_0\mkern-1.5mu}\mkern 1.5mu}^k \\ &= \sum_{k\geq 0}\mkern 1.5mu\overline{\mkern-1.5muc_k\mkern-1.5mu}\mkern 1.5mu \qty{z - w_0}^k ,\end{align*} which yields a power series expansion of \(F\) about \(w_0\). So \(f\) is analytic at every point in \(\tilde S\) and thus holomorphic. Since \(\mkern 1.5mu\overline{\mkern-1.5muf(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu = f(z)\) for \(z, f(z)\in {\mathbb{R}}\), \(F\) is a continuous extension of \(f\) to \({\mathbb{D}}\). By the symmetry principle, \(F\) is holomorphic, and \({ \left.{{F}} \right|_{{S}} } = f\).
Blaschke Factors
Spring 2019.5, Spring 2021.5 (Blaschke contraction)
^14ad86
Let \(f\) be a holomorphic map of the open unit disc \({\mathbb{D}}\) to itself. Show that for any \(z, w\in {\mathbb{D}}\), \begin{align*} \left|\frac{f(w)-f(z)}{1-\overline{f(w)} f(z)}\right| \leq\left|\frac{w-z}{1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}\right| .\end{align*} Show that this inequality is strict for \(z\neq w\) except when \(f\) is a linear fractional transformation from \({\mathbb{D}}\) to itself.
The Schwarz conjugation trick:
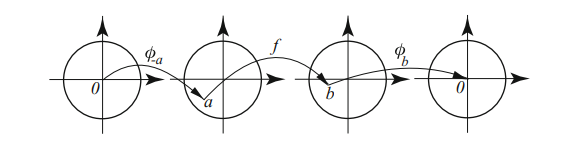
Write the RHS as \(a\), we then want something in the form \({\left\lvert {F(a)} \right\rvert}\leq {\left\lvert {a} \right\rvert}\). The choice \(a=\psi_w(z)\) is forced, so \(z= \psi_w^{-1}(a)\). This forces the choice for the LHS \begin{align*} { f(w) - (f\circ \psi_w^{-1})(a) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(w)\mkern-1.5mu}\mkern 1.5mu (f\circ \psi_w^{-1})(a) } = (\psi_{f(w)} \circ f \circ \psi_w^{-1})(a) \coloneqq F(a) .\end{align*}
This is the Schwarz–Pick lemma.
-
Fix \(z_1\) and let \(w_1 = f(z_1)\). Define \begin{align*} \psi_{a}(z) \coloneqq{a-z \over 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5muz} \in \mathop{\mathrm{Aut}}({\mathbb{D}}) .\end{align*}
- Note that inequality now reads \begin{align*} {\left\lvert {\psi_{f(w)}(f(z)) } \right\rvert} \leq {\left\lvert {\psi_w(z)} \right\rvert} .\end{align*} Moreover \(\psi_a\) is an involution that swaps \(a\) and \(0\).
-
Now set up a situation where Schwarz’s lemma will apply: \begin{align*} 0 \xrightarrow{\psi_{z_1}} z_1 \xrightarrow{f} f(z) \xrightarrow{\psi_{f(z_1)}} 0 ,\end{align*} so \(F\coloneqq\psi_{f(z_1)} \circ f \circ \psi_{z_1} \in \mathop{\mathrm{Aut}}({\mathbb{D}})\) and \(F(0) = 0\).
-
Apply Schwarz we get \({\left\lvert {F(z)} \right\rvert} \leq {\left\lvert {z} \right\rvert}\) for all \(z\), so \begin{align*} {\left\lvert {F(z)} \right\rvert} &\leq {\left\lvert {z} \right\rvert} \\ \implies {\left\lvert { f(z_1) - (f\circ \psi_{z_1})(z) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(z_1)\mkern-1.5mu}\mkern 1.5mu \cdot (f\circ \psi_{z_1}) (z) } \right\rvert} &\leq {\left\lvert { z} \right\rvert} \\ \implies {\left\lvert {f(z_1) - f(w) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(z_1)\mkern-1.5mu}\mkern 1.5mu\cdot f(w) } \right\rvert} &\leq {\left\lvert {\psi_{z_1}(z)} \right\rvert} && w\coloneqq\psi_{z_1}(z) \\ \implies {\left\lvert {f(z_1) - f(w) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(z_1)\mkern-1.5mu}\mkern 1.5mu\cdot f(w) } \right\rvert} &\leq {\left\lvert {z_1 - z \over 1 - \mkern 1.5mu\overline{\mkern-1.5muz_1\mkern-1.5mu}\mkern 1.5mu z } \right\rvert} .\end{align*}
-
Since \(z_1\) was arbitrary and fixed and \(w\) was a free variable, this holds for all \(z,w\in {\mathbb{D}}\).
-
Strictness: suppose equality holds, we’ll show that \(f(z) = {az+b\over cz+d}\)
-
By Schwarz, \(F(z) = \lambda z\) for \(\lambda \in S^1\). Thus \begin{align*} (\psi_{f(z_1)} \circ f \circ \psi_{z_1}) (z) &= \lambda z \\ \implies (f \circ \psi_{z_1}) (z) &= \psi_{f(z_1)}^{-1}(\lambda z ) \\ \implies f(w) &= \psi_{f(z_1)}^{-1}(\lambda \psi_{z_1}^{-1}(w) ) && w\coloneqq\psi_{z_1}(z) \\ &= \psi_{f(z_1)} \qty{\lambda \psi_{z_1}(w)} \\ &= \lambda \psi_{\mkern 1.5mu\overline{\mkern-1.5mu\lambda \mkern-1.5mu}\mkern 1.5muf(z_1)} \qty{\psi_{z_1}(w)} \\ &\coloneqq\lambda \psi_a(\psi_b(w)) \\ &=\lambda\qty{ a- \psi_b(w) \over 1 - \mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu \psi_b(w) } \\ &= \quad \vdots \\ &= -\lambda \qty{ \frac{{\left(a \overline{b} - 1\right)} z - a + b}{{\left(\overline{a} - \overline{b}\right)}z - b \overline{a} + 1} } \\ &= \qty{ \frac{-\lambda {\left(a \overline{b} - 1\right)} z + \lambda( a - b)}{{\left(\overline{a} - \overline{b}\right)}z + (- b \overline{a} + 1)} } ,\end{align*} which is evidently a linear fractional transformation.
Schwarz-Pick derivative
Suppose \(f:{\mathbb{D}}\to {\mathbb{D}}\) is analytic. Prove that \begin{align*} \forall a\in {\mathbb{D}}, \qquad {{\left\lvert {f'(a)} \right\rvert} \over 1 - {\left\lvert {f(a)} \right\rvert}^2 } \leq {1 \over 1 - {\left\lvert {a} \right\rvert}^2} .\end{align*}
Holomorphic maps on \({\mathbb{D}}\) contract Blaschke factors: \begin{align*} {\left\lvert { \psi_w(z) } \right\rvert} \geq {\left\lvert {\psi_{f(w)}(f(z)) } \right\rvert} ,\end{align*} i.e. \begin{align*} {\left\lvert {f(w) - f(z) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(w)\mkern-1.5mu}\mkern 1.5muf(z)} \right\rvert} \leq {\left\lvert {w-z \over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} .\end{align*}
Make a change of variables \(a\coloneqq\psi_w(z)\) so \(z=\psi_w^{-1}(a) = \psi_w(a)\), then the desired inequality follows if we can show \begin{align*} {\left\lvert { \psi_{f(w)}(f(\psi_w(a))) } \right\rvert} \leq {\left\lvert {a} \right\rvert} .\end{align*}
So define \(F \coloneqq\psi_{f(w)} \circ f \circ \psi_w\), then since \(\psi_w(0) = w\), \begin{align*} F(0) = \psi_{f(w)}(f(w)) = 0 .\end{align*} Moreover \({\left\lvert {F(z)} \right\rvert}\leq 1\) since each constituent is a map \({\mathbb{D}}\to {\mathbb{D}}\). So \(F\) satisfies Schwarz and the claim follows.
Given this, there’s just a clever rearrangement to obtain the stated result: \begin{align*} {\left\lvert {f(w) - f(z) \over 1 - \mkern 1.5mu\overline{\mkern-1.5muf(w)\mkern-1.5mu}\mkern 1.5muf(z)} \right\rvert} &\leq {\left\lvert {w-z \over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z} \right\rvert} \\ \implies {\left\lvert { 1\over 1-\mkern 1.5mu\overline{\mkern-1.5muf(w)\mkern-1.5mu}\mkern 1.5muf(z) } \right\rvert} \cdot {\left\lvert {f(z) - f(w) \over z-w} \right\rvert} &\leq {\left\lvert {1\over 1-\mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5muz} \right\rvert} \\ ,\end{align*} and taking \(z\to w\) on both sides yields \begin{align*} {\left\lvert {1\over 1 - {\left\lvert {f(w)} \right\rvert}^2 } \right\rvert} {\left\lvert {f'(w)} \right\rvert} \leq {1\over {\left\lvert {w} \right\rvert}^2} \implies {\left\lvert {f'(w)} \right\rvert} \leq {1-{\left\lvert {f(w)} \right\rvert}^2\over 1-{\left\lvert {w} \right\rvert}^2 } .\end{align*}
Schwarz and Blaschke products
Suppose \(f:{\mathbb{D}}\to{\mathbb{D}}\) is analytic and admits a continuous extension \(\tilde f: \mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\to \mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) such that \({\left\lvert {z} \right\rvert} = 1 \implies {\left\lvert {f(z)} \right\rvert} = 1\).
-
Prove that \(f\) is a rational function.
-
Suppose that \(z=0\) is the unique zero of \(f\). Show that \begin{align*} \exists n\in {\mathbb{N}}, \lambda \in S^1 {\quad \operatorname{ such that } \quad}f(z) = \lambda z^n .\end{align*}
- Suppose that \(a_1, \cdots, a_n \in {\mathbb{D}}\) are the zeros of \(f\) and prove that \begin{align*} \exists \lambda \in S^1 {\quad \operatorname{such that} \quad} f(z) = \lambda \prod_{j=1}^n {z - a_j \over 1 - \mkern 1.5mu\overline{\mkern-1.5mua_j\mkern-1.5mu}\mkern 1.5mu z} .\end{align*}
Part 1: use the reflection principle to define \begin{align*} F(z) \coloneqq \begin{cases} f(z) & {\left\lvert {z} \right\rvert} \leq 1 \\ {1\over \mkern 1.5mu\overline{\mkern-1.5muf\qty{1/\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu}\mkern-1.5mu}\mkern 1.5mu } & {\left\lvert {z} \right\rvert} \geq 1 \end{cases} .\end{align*}
Now \(F:{\mathbb{CP}}^1\to {\mathbb{CP}}^1\) is holomorphic and all such functions are rational. As a consequence, \(f\) is rational.
Part 2: As in the proof of Schwarz, define \(g(z) \coloneqq{f(z)\over z^n}\) where \(n = {\operatorname{Ord}}_{f}(0)\). Then \(g\) is holomorphic on \({\mathbb{D}}\) since the singularity at \(z=0\) is removable. On \({\left\lvert {z} \right\rvert} = r<1\), \begin{align*} {\left\lvert {g(z)} \right\rvert} = { {\left\lvert {f(z)} \right\rvert} \over {\left\lvert {z} \right\rvert} } = {{\left\lvert {f(z)} \right\rvert} \over r} \leq {1\over r} \overset{r\to 1^-}\longrightarrow 1 ,\end{align*} using that \({\left\lvert {f} \right\rvert} \leq 1\) on \({\mathbb{D}}\). By the MMP, \({\left\lvert {g} \right\rvert} \leq 1\) on all of \({\mathbb{D}}\). Note that \({\left\lvert {g} \right\rvert} = 1\) when \({\left\lvert {z} \right\rvert}=1\), so \({\left\lvert {1/g} \right\rvert}\leq 1\) in \({\mathbb{D}}\) by the MMP, forcing \({\left\lvert {g} \right\rvert} = 1\). Unwinding this, \({\left\lvert {f} \right\rvert} = {\left\lvert {z} \right\rvert}^n\), go \(f(z) = \lambda z^n\) for some \({\left\lvert {\lambda} \right\rvert} = 1\).
Part 3: Define \(\Psi(z) \coloneqq\prod_{k\leq n} \psi_{a_k}(z)\) where \(\psi_a(z) \coloneqq{a-z\over 1-\mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5mu z}\). Set \(g(z) \coloneqq{f(z) \over \Psi(z)}\), then by the same argument as above, \({\left\lvert {g} \right\rvert} \leq 1\) and \({\left\lvert {g} \right\rvert} = 1\) on \({\left\lvert {z} \right\rvert} = 1\). Then \(g\) has no zeros, since they’ve all been divided out, and no poles since \(f\) is holomorphic on \({\mathbb{D}}\), so \(1/g\) is holomorphic on \({\mathbb{D}}\). Since \({\left\lvert {1/g} \right\rvert} = 1\) on \(S^1\), this forces \(g\) to be constant. Equality in the Schwarz lemma implies \(g(z) = \lambda z\) is a rotation, and unwinding this yields \(f(z) = \lambda \Psi(z)\).
Tie’s Extra Questions: Fall 2009
Let \(g\) be analytic for \(|z|\leq 1\) and \(|g(z)| < 1\) for \(|z| = 1\).
-
Show that \(g\) has a unique fixed point in \(|z| < 1\).
-
What happens if we replace \(|g(z)| < 1\) with \(|g(z)|\leq 1\) for \(|z|=1\)? Give an example if (a) is not true or give an proof if (a) is still true.
-
What happens if we simply assume that \(f\) is analytic for \(|z| < 1\) and \(|f(z)| < 1\) for \(|z| < 1\)? Suppose that \(f(z) \not\equiv z\). Can f have more than one fixed point in \(|z| < 1\)?
Hint: The map \(\displaystyle{\psi_{\alpha}(z)=\frac{\alpha-z}{1-\mkern 1.5mu\overline{\mkern-1.5mu\alpha\mkern-1.5mu}\mkern 1.5muz}}\) may be useful.
Use Rouché: if \({\left\lvert {f(z)} \right\rvert} < 1\) is strict when \({\left\lvert {z} \right\rvert} = 1\), then consider \(F(z) \coloneqq f(z) - z\). Write the big part as \(M(z) = z\) and the small as \(m(z) = f(z)\), then on \({\left\lvert {z} \right\rvert} = 1\) \begin{align*} {\left\lvert {m(z)} \right\rvert} = {\left\lvert {f(z)} \right\rvert} < 1 = {\left\lvert {z} \right\rvert} = {\left\lvert {M(z)} \right\rvert} ,\end{align*} so \(M(z)\) and \(m(z) + M(z) = f(z) - z\) have the same number of zeros in \({\mathbb{D}}\) – precisely one.
There is still a unique fixed point. Use the Brouwer fixed point theorem: since \(g\) is holomorphic on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\), it is in particular continuous. By the Brouwer fixed point theorem, every continuous map \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu \to \mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\) has a fixed point. If \(g\) is nonconstant, then the fixed point is unique by Schwarz: without loss of generality one can assume \(f(0) = 0\) by composing with a Blaschke factor. Apply Schwarz to \(f\), then if \(f(a) = a\) we have the equality clause and \(f(z) = \lambda z\). Since \(a = f(a) = \lambda a\), \(\lambda = 1\) and \(f\) is the identity. If \(g\) is constant, then \({\left\lvert {g(z)} \right\rvert} < 1\) on \({\left\lvert {z} \right\rvert} = 1\) forces \(g\equiv 0\).
Note that there is a major difference between self maps to \({\mathbb{D}}\) versus \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\). By the argument in part 2, if \(f(z)\) is not the identity then \(f\) can have at most one fixed point. Moreover, not every map \(f:{\mathbb{D}}\to{\mathbb{D}}\) need have a fixed point: consider \begin{align*} g: {\mathbb{H}}&\to {\mathbb{H}}\\ z &\mapsto z+1 .\end{align*} Now conjugate with the Cayley map \(C:{\mathbb{H}}\to {\mathbb{D}}\) to define \(f\coloneqq CgC^{-1}:{\mathbb{D}}\to {\mathbb{D}}\) which has no fixed points at all.
Tie’s Extra Questions: Fall 2015 (Blaschke factor properties) #complex/exercises/completed
-
Let \(z, w\) be complex numbers, such that \(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu w \neq 1\). Prove that \begin{align*}{\left\lvert {\frac{w - z}{1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}} \right\rvert} < 1 \; \; \; \mbox{if} \; |z| < 1 \; \mbox{and}\; |w| < 1,\end{align*} and also that \begin{align*}{\left\lvert {\frac{w - z}{1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}} \right\rvert} = 1 \; \; \; \mbox{if} \; |z| = 1 \; \mbox{or}\; |w| = 1.\end{align*}
-
Prove that for fixed \(w\) in the unit disk \(\mathbb D\), the mapping \begin{align*}F: z \mapsto \frac{w - z}{1 - \mkern 1.5mu\overline{\mkern-1.5muw\mkern-1.5mu}\mkern 1.5mu z}\end{align*} satisfies the following conditions:
-
\(F\) maps \(\mathbb D\) to itself and is holomorphic.
-
\(F\) interchanges \(0\) and \(w\), namely, \(F(0) = w\) and \(F(w) = 0\).
-
\({\left\lvert {F(z)} \right\rvert} = 1\) if \(|z| = 1\).
-
\(F: {\mathbb D} \mapsto {\mathbb D}\) is bijective.
-
Hint: Calculate \(F \circ F\).
Tie’s Extra Questions: Spring 2015
Suppose \(f\) is analytic in an open set containing the unit disc \(\mathbb D\) and \(|f(z)| =1\) when \(|z|\)=1. Show that either \(f(z) = e^{i \theta}\) for some \(\theta \in \mathbb R\) or there are finite number of \(z_k \in \mathbb D\), \(k \leq n\) and \(\theta \in \mathbb R\) such that \begin{align*} \displaystyle f(z) = e^{i\theta} \prod_{k=1}^n \frac{z-z_k}{1 - \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu_k z } \, . .\end{align*}
Also cf. Stein et al, 1.4.7, 3.8.17
Tie’s Extra Questions: Spring 2015 (Equality of modulus)
Let \(f\) and \(g\) be non-zero analytic functions on a region \(\Omega\). Assume \(|f(z)| = |g(z)|\) for all \(z\) in \(\Omega\). Show that \(f(z) = e^{i \theta} g(z)\) in \(\Omega\) for some \(0 \leq \theta < 2 \pi\).
Define \(F(z) \coloneqq{f(z) \over g(z)}\).
\(F\) is holomorphic on \(\Omega\).
Note that \(g(a) = 0\) iff \(f(a) = 0\), so \(F\) has no poles. If \(F\) has a singularity at \(z_0\), noting that \({\left\lvert {F(z_0)} \right\rvert} = 1\), \(F\) is bounded in a neighborhood of \(z_0\) and thus the singularity must be removable. By Riemann’s removable singularity theorem, \(F\) extends to a holomorphic function.
Given this, note that \({\left\lvert {F(z)} \right\rvert} = 1\) for all \(z\), so \(F(\Omega) \subseteq S^1\), which is codimension 1 in \({\mathbb{C}}\) and not open. By the open mapping theorem, \(F\) must be constant, so \(F(z) = \lambda\), and in particular since \({\left\lvert {F(z)} \right\rvert} = 1\), \(\lambda = e^{it}\in S^1\) for some \(t\). Then \(f(z) = \lambda g(z)\).
Fixed Points
Fall 2020.7
^4c605e
Suppose that \(f: \mathbb{D} \rightarrow \mathbb{D}\) is holomorphic and \(f(0)=0\). Let \(n \geq 1\), and define the function \(f_{n}(z)\) to be the \(n\)-th composition of \(f\) with itself; more precisely, let
\begin{align*} f_{1}(z):=f(z), f_{2}(z):=f(f(z)), \text { in general } f_{n}(z):=f\left(f_{n-1}(z)\right) . \end{align*}
Suppose that for each \(z \in \mathbb{D}, \lim _{n \rightarrow \infty} f_{n}(z)\) exists and equals to \(g(z)\). Prove that either \(g(z) \equiv 0\) or \(g(z)=z\) for all \(z \in D\).
Note that there is a unique fixed point. We have \(f(0) = 0\), so there is at least one, so suppose \(a\) is another fixed point with \(f(a) = a\). By Schwarz, \({\left\lvert {f(z)} \right\rvert}\leq {\left\lvert {z} \right\rvert}\) with equality at any nonzero point implying \(f\) is a rotation, and \(f(a) = a\implies {\left\lvert {f(a)} \right\rvert} = {\left\lvert {a} \right\rvert}\), so write \(f(z) = e^{i\theta}z\). Now \(f(a) = a = e^{i\theta }a\) forces \(\theta = 0\), so \(f(z) = z\) is the identity.
Since \(f(0) = 0\), the Schwarz lemma applies and either
- \(f(z) = e^{i\theta} z\) is a rotation, or
- \({\left\lvert {f'(0)} \right\rvert} < 1\) and \({\left\lvert {f(z)} \right\rvert} < z\) for all \(z\in {\mathbb{D}}\).
Supposing the latter, \(f\) is a contraction, and \({\left\lvert {f_{n+1}(z)} \right\rvert} < {\left\lvert {f_{n}(z)} \right\rvert}\) for all \(n\) and all \(z\), so \({\left\lvert {f_n(z)} \right\rvert} \overset{n\to\infty}\longrightarrow 0\) for all \(z\). Since \(f_n\to g\) pointwise, this means \(g(z) = 0\) for all \(z\), making \(g\equiv 0\).
Otherwise, suppose \(f\) is a rotation. Then if \(f(z) = e^{i\theta}z\), \(f_n(z) = e^{in\theta}z\). The pointwise limit \(\lim_{n\to\infty}e^{in\theta}z\) can only exist if \(\theta = 0\), otherwise this is periodic when \(\theta\) is rational or the points \(e^{i\theta}z, e^{2i\theta }z,\cdots\) form form a countably infinite set of distinct points. So \(f(z) = z\), making \(\lim_{n\to \infty}f_n(z) = z\) as well.
Open Mapping, Riemann Mapping, Casorati-Weierstrass
Spring 2020.6 (Prove the open mapping theorem)
^128e58
Prove the open mapping theorem for holomorphic functions: If \(f\) is a non-constant holomorphic function on an open set \(U\) in \(\mathbb{C}\), then \(f(U)\) is also an open set.
Idea:
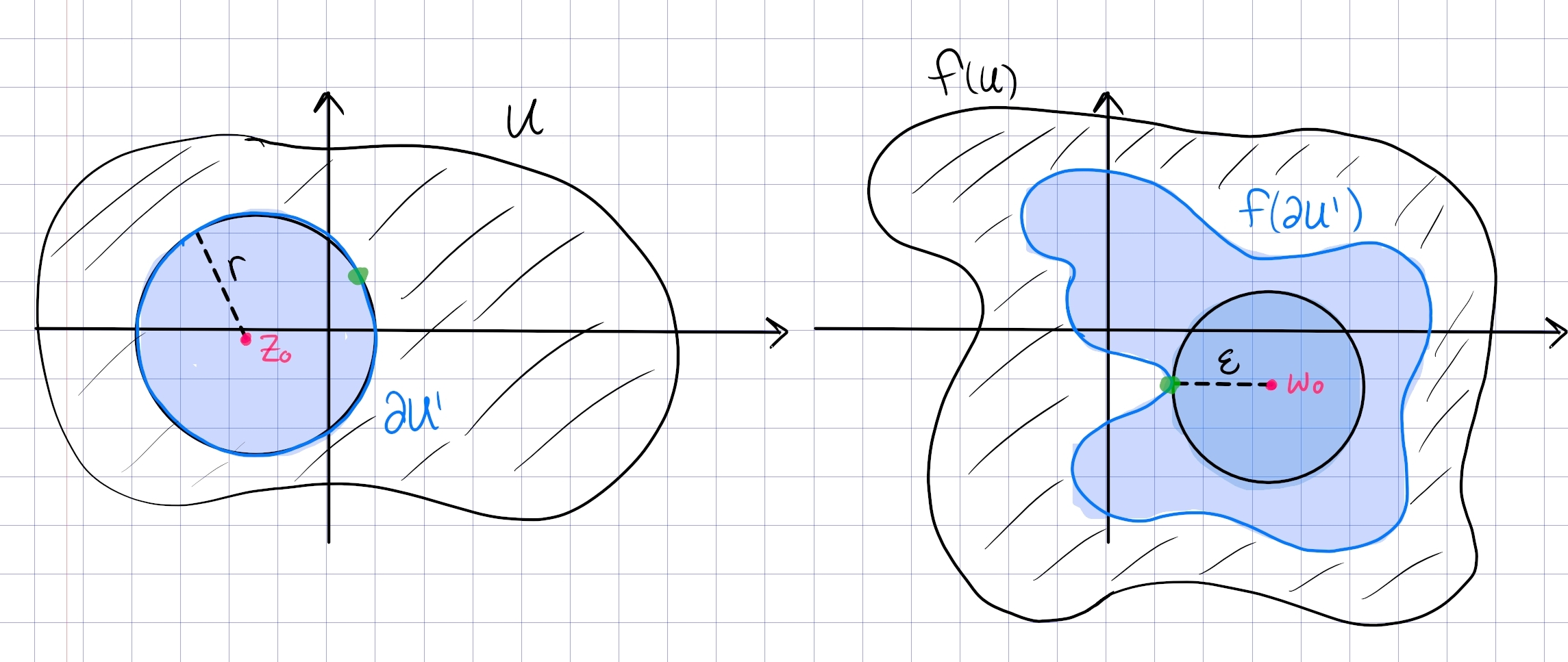
Let \(f: U\to {\mathbb{C}}\). Pick \(w_0\in W\) with \(f(z_0) = w_0\) for some \(z_0\in U\); we want to show that \(w_0\) is an interior point of \(f(U)\), so we’re looking for a disc containing \(w_0\) and contained in \(f(U)\).
Write \begin{align*} g_0(z) \coloneqq f(z) - w_0 ,\end{align*} so \(g_0\) is holomorphic and has a zero at \(z_0\). Since zeros of holomorphic functions are isolated, there is some \(U' \coloneqq{\mathbb{D}}_r(z_0)\) where \(g_0\) is nonvanishing. The claim is that if we choose \({\varepsilon}\) small enough, we can arrange so that \(W_{\varepsilon}\coloneqq{\mathbb{D}}_{\varepsilon}(w_0) \subseteq f(U)\). This will follow if for every \(w\in W_{\varepsilon}\), the equation \(f(z) = w\) has a solution in \(U\), i.e. Define a function that counts the number of zeros: \begin{align*} F(w) &\coloneqq{1\over 2\pi i}\int_{{{\partial}}U' } {f(z) \over f(z) - w_1 }\,dz\\ &= {1\over 2\pi i}\int_{{{\partial}}U' } {{\frac{\partial }{\partial z}\,}\qty{f(z) - w} \over f(z) - w }\,dz\\ &= {\sharp}Z(f(z) - w, U' ) ,\end{align*} which is the number of zeros of \(f(z) - w\) in \(U'\) by the argument principle. Now \(F\) is a \({\mathbb{Z}}{\hbox{-}}\)valued function, and the only obstruction to continuity is if \(f(z) - w = 0\) in the integrand for some \(z\). The claim is that \({\varepsilon}\) can be chosen such \begin{align*} z\in {{\partial}}U' \implies {\left\lvert {f(z) - w} \right\rvert} > 0 \qquad \forall w\in W_{\varepsilon} .\end{align*} The theorem then follows immediately: \(F(w): U' \to W_{\varepsilon}\) is a continuous and \({\mathbb{Z}}{\hbox{-}}\)valued, thus constant. Then noting that \(F(w_0) = 1\) since \(z_0\in U'\) and \(w_0\in W_{\varepsilon}\), we have \(F\equiv 1 > 0\) for all \(w\).
Choose \begin{align*} {\varepsilon}\coloneqq\min_{z\in {{\partial}}U'}{\left\lvert {f(z) - w_0} \right\rvert} .\end{align*} Now if \({\left\lvert {w-w_0} \right\rvert} < {\varepsilon}\) and \({\left\lvert {z-z_0} \right\rvert} = r\), we have \({\left\lvert {f(z) - w} \right\rvert} > {\varepsilon}> 0\).
Fall 2019.4, Spring 2020 HW 3 SS 3.8.14, Tie’s Extras Fall 2009, Problem Sheet (Entire univalent functions are linear)
^398dec
Let \(f: \mathbb{C} \rightarrow \mathbb{C}\) be an injective analytic (also called univalent) function. Show that there exist complex numbers \(a \neq 0\) and \(b\) such that \(f(z)=a z+b\).
Hint: Apply the Casorati-Weierstrass theorem to \(f(1/z)\).
Note that \(f\) is non-constant, since a constant function is extremely non-injective. Consider the singularity at \(\infty\):
-
If it is removable, then \(f\) is bounded outside of a large disc, and bounded inside of it as a continuous function on a compact set, making \(f\) entire and bounded and thus constant by Liouville.
-
If it is essential, then by Casorati-Weierstrass there is a large disc of radius \(R\) such that \(f(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}_R\mkern-1.5mu}\mkern 1.5mu^c) \subseteq {\mathbb{C}}\) is dense. By the open mapping theorem, \(f({\mathbb{D}}_R) \subseteq {\mathbb{C}}\) is open, so by density it intersects \(f(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}_R\mkern-1.5mu}\mkern 1.5mu^c)\), but \({\mathbb{D}}_R \cap\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}_R\mkern-1.5mu}\mkern 1.5mu^c\) is empty so this contradicts injectivity.
So we can conclude \(\infty\) is a pole of some order \(N\), so \(f\qty{1\over z} = \sum_{0\leq k\leq N} c_k z^{-k}\) and thus \(f(z) = \sum_{0\leq k\leq N} c_k z^k\) is a polynomial of degree \(N\). However, a polynomial of degree \(N\) is generically \(N\)-to-one locally, so injectivity forces \(N=1\) and \(f(z) = c_0 + c_1 z\), where \(c_1\neq 0\) since \(f\) is nonconstant.
Write \(g(z) \coloneqq f(1/z)\), which has a singularity at \(z=0\). The claim is that this is a pole.
If \(z=0\) is a removable singularity, \(g\) is bounded on some closed disc \({\left\lvert {z} \right\rvert} \leq {\varepsilon}\), so \(f\) is bounded on \({\left\lvert {z} \right\rvert} > {\varepsilon}\). Moreover \(f\) is continuous and \({\left\lvert {z} \right\rvert}\leq {\varepsilon}\), \(f\) is bounded on this disc. This makes \(f\) an entire bounded function and thus constant by Liouville, contradicting injectivity.
If \(z=0\) is essential, then by Casorati-Weierstrass pick a punctured disc \(D = \left\{{{\left\lvert {z} \right\rvert} \leq {\varepsilon}}\right\}\) where \(g(D)\) is dense in \({\mathbb{C}}\). Writing \(D^c \coloneqq\left\{{{\left\lvert {z} \right\rvert} > {\varepsilon}}\right\}\), this means that \(f(D^c)\) is dense. But \(U\coloneqq\left\{{{\left\lvert {z} \right\rvert} < {\varepsilon}}\right\}\) is open and by the open mapping theorem \(f(U)\) is open, so by density there is a point \(w\in f(D^c) \cap f(U)\) while \(U \cap D^c = \emptyset\), again contradicting injectivity.
So \(z=0\) is a pole of \(g\), and \(g\) admits a Laurent expansion \begin{align*} g(z) = \sum_{k\geq -N} c_k z^k .\end{align*} Since \(f\) is entire, it equals its Laurent expansion at \(z=0\), so equating the two series yields \begin{align*} f(z) = \sum_{k\geq 0} d_k z^k &\implies g(z) = \sum_{k\geq 0} {d_k \over z^k} = \sum_{1\leq k\leq N} {c_k\over z^k} + \sum_{k\geq 0} c_k z^k \\ &\implies \sum_{k\geq 0} c_k z^k = 0 \\ &\implies f(z) = \sum_{0\leq k \leq N} c_k z^k ,\end{align*} making \(f\) a polynomial of degree at most \(N\).
Now \(f\) can not be degree zero, since constant maps are not injective. Moreover \(f\) can not be degree \(N\geq 2\), since any polynomial of degree \(N\) has \(N\) roots in \({\mathbb{C}}\) by the fundamental theorem of algebra, and any two distinct roots will be points where injectivity fails. Finally, ruling out the case of roots with multiplicity, if \(f(z) = c(z-a)^N\), then \(f\) has exactly \(N\) preimages in a neighborhood of \(a\). Letting \(p\) be any such point, we can find \(N\) complex points mapping to it: \begin{align*} p = c(z-a)^N &\implies {p\over c} = (z-a)^N \\ &\implies \qty{p\over c}^{1\over N}\zeta_N^k = z-a \quad k=0,1,\cdots, n-1 \\ &\implies z_k\coloneqq\qty{p\over c}^{1\over N}\zeta_N^k + a \xrightarrow{f} p .\end{align*}
So \(f\) must be degree exactly 1, i.e. \(f(z) = az+b\).
Tie’s Extra Questions: Spring 2015
-
Let \(f\) be analytic in \(\Omega: 0<|z-a|<r\) except at a sequence of poles \(a_n \in \Omega\) with \(\lim_{n \rightarrow \infty} a_n = a\). Show that for any \(w \in \mathbb C\), there exists a sequence \(z_n \in \Omega\) such that \(\lim_{n \rightarrow \infty} f(z_n) = w\).
-
Explain the similarity and difference between the above assertion and the Weierstrass-Casorati theorem.
DZG: I think it’s also necessary to state that \(z_n \to a\).
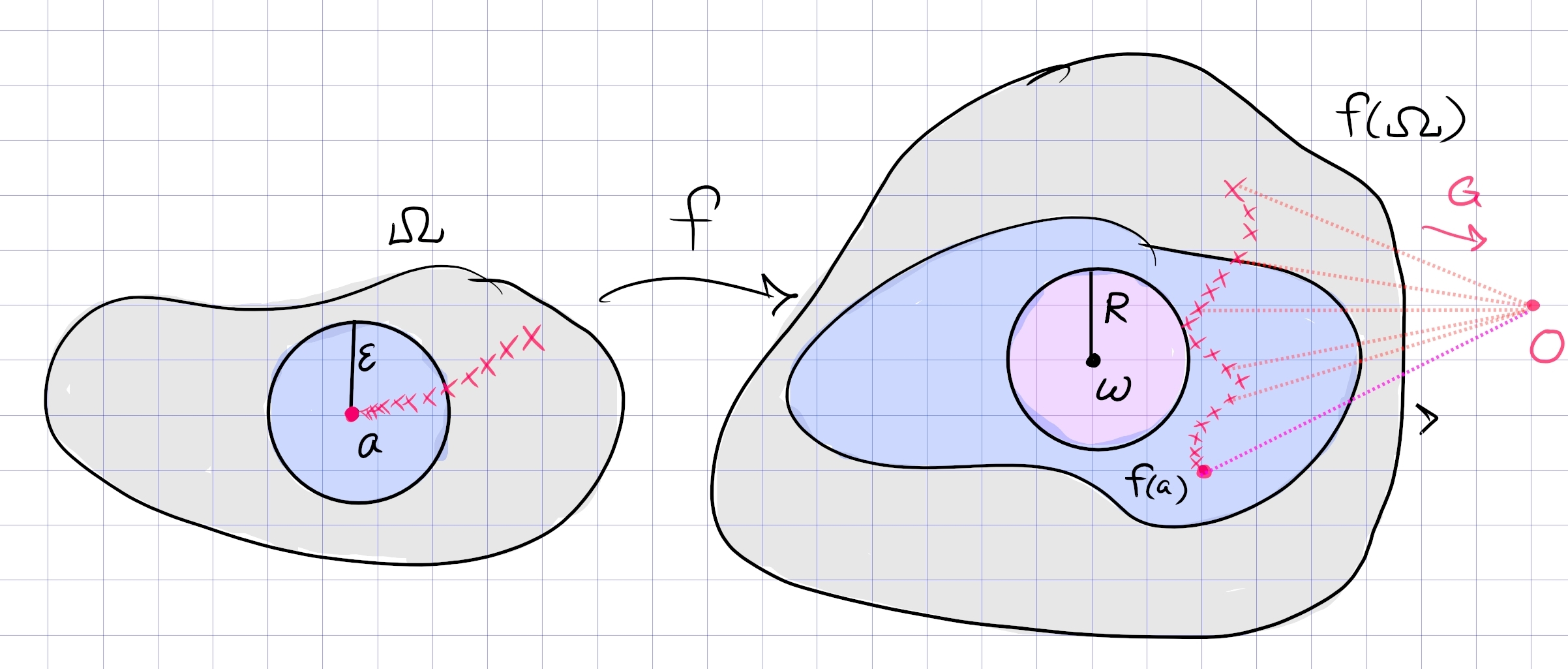
As in the proof of Casorati-Weierstrass, fix \(w\) and suppose toward a contradiction that no sequence sequence exists. Then there is some \({\varepsilon}, R\) such that \begin{align*} f({\mathbb{D}}_{\varepsilon}(a)) \subseteq {\mathbb{D}}_R(w)^c ,\end{align*} for otherwise one could construct the desired sequence. In particular, \({\left\lvert {f(z) - w} \right\rvert} > R\) for \({\left\lvert {z-a} \right\rvert} < {\varepsilon}\), so define \begin{align*} G(z) \coloneqq{1\over f(z) - w} \implies {\left\lvert {G(z)} \right\rvert} \leq R^{-1}< \infty \qquad \text{in }{\mathbb{D}}_{\varepsilon}(a) .\end{align*} Since \(G\) is bounded in this disc, any singularities here must be removable. Since the \(a_k\) are poles of \(f\), they are zeros of \(G\) – this is because if \({\left\lvert {f(z)} \right\rvert}\to\infty\) as \(z\to a_k\) then \({\left\lvert {G(z)} \right\rvert}\to 0\). So \(G(a_k) = 0\) for all \(k\) and \(G\) extends holomorphically over the removable singularity \(a\), and by continuity must satisfies \(G(a) = 0\). But now \(G\) is zero on a set with a limit point, hence \(G\equiv 0\) by the identity principle. This is a contradiction since if \(G\equiv 0\) on an open set, \(f\) has poles on an open set, contradicting that \(f\) is holomorphic on \(\Omega\).
The difference to Casorati-Weierstrass: the singularity at \(a\) is not essential, since in particular it is not isolated. The conclusion is nearly the same though: this says that every \(w\in {\mathbb{C}}\) is a limit point for \(f(\Omega)\), so \(w\) is in the closure of \(f(\Omega)\), making the image dense in \({\mathbb{C}}\).
Dense images #stuck
Suppose \(f: {\mathbb{H}}\cup{\mathbb{R}}\to {\mathbb{C}}\) satisfies the following:
- \(f(i) = i\)
- \(f\) is continuous
- \(f\) is analytic on \({\mathbb{H}}\)
- \(f(z) \in {\mathbb{R}}\iff z\in {\mathbb{R}}\).
Show that \(f({\mathbb{H}})\) is a dense subset of \({\mathbb{H}}\).
Ideas:
- If an entire function doesn’t have dense image, it’s constant by Liouville using the proof idea of Casorati-Weierstrass.
- Conjugate \(f\) by \(T:{\mathbb{H}}\to {\mathbb{D}}\) where \(T(z) = {z-i\over z+i}\), then \(\tilde f(0) = 0\)
- Use that \(T({\mathbb{R}}) = S^1\), so \({\left\lvert {\tilde f(z)} \right\rvert} = 1\) when \({\left\lvert {z} \right\rvert} = 1\).
- Schwarz reflection applies to \(\tilde f\) to define an entire function – if \(f\) isn’t dense, then the extension of \(\tilde f\) isn’t dense…?
- No clue how to use \(f(i) = i\), although it implies \(\tilde f(0) = 0\) and Schwarz applies.
Tie’s Extra Questions: Spring 2015
Let \(f(z)\) be an analytic function on \({\mathbb C} \backslash \{ z_0 \}\), where \(z_0\) is a fixed point. Assume that \(f(z)\) is bijective from \({\mathbb C} \backslash \{ z_0 \}\) onto its image, and that \(f(z)\) is bounded outside \(D_r(z_0)\), where \(r\) is some fixed positive number. Show that there exist \(a, b, c, d \in \mathbb C\) with \(ad-bc \neq 0\), \(c \neq 0\) such that \(\displaystyle f(z) = \frac{az + b}{cz + d}\).
Schwarz Reflection
Tie’s Extra Questions: Spring 2015 (Reflection for harmonic functions)
-
Assume \(u\) is harmonic on open set \(O\) and \(z_n\) is a sequence in \(O\) such that \(u(z_n) = 0\) and \(\lim z_n \in O\). Prove or disprove that \(u\) is identically zero. What if \(O\) is a region?
-
Assume \(u\) is harmonic on open set \(O\) and \(u(z) = 0\) on a disc in \(O\). Prove or disprove that \(u\) is identically zero. What if \(O\) is a region?
-
Formulate and prove a Schwarz reflection principle for harmonic functions
cf. Theorem 5.6 on p.60 of Stein et al.
Hint: Verify the mean value property for your new function obtained by Schwarz reflection principle.
Part 1: This is not true: take the holomorphic function \(f(z) = z\), then \(u(z) \coloneqq\Re(f(z)) = \Re(z)\) is harmonic on nonzero on \({\mathbb{R}}\) but zero on \(i{\mathbb{R}}\).
Part 2: Set \(f \coloneqq u_x + i u_y\), then \(f\) is holomorphic on \(O\). Since \(h\equiv 0\) on \({\mathbb{D}}_{\varepsilon}\subseteq O\), \(g\equiv 0\) on this disc. By the identity principle for holomorphic functions, \(g\equiv 0\) on \(O\). So \(h_x, h_y \equiv 0\), making \(h\) constant, and since \(h\equiv 0\) on \(U\) this forces \(h\equiv 0\) on \(O\).
Part 3: Let \(u\) be harmonic on \(S^+\), a region symmetric about \({\mathbb{R}}\), and that \(u\equiv 0\) on \({\mathbb{R}}\cap S^+\). Define \(S^- = \left\{{\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu {~\mathrel{\Big\vert}~}z\in S^+}\right\}\), and \begin{align*} U(z) \coloneqq \begin{cases} U(z) & z\in S^+ \\ -U(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu) & z\in S^-. \end{cases} .\end{align*} Then \(U\) is a harmonic extension of \(u\) to \(S \coloneqq S^+ \cup(S^+ \cap{\mathbb{R}}) \cup S^-\). To see that \(U\) is harmonic on \(S\), it suffices to check that \(U\) satisfies the mean value property on \(S\). Clearly this holds in \(S^+\), so for \(z_0\in S^+\) we have \begin{align*} U(z_0) &= u(z_0) \\ &= {1\over 2\pi} \int_{-\pi}^\pi u(z_0 + re^{it} )\,dt\\ &= {1\over 2\pi} \int_{-\pi}^\pi U(z_0 + re^{it} )\,dt\\ .\end{align*} So for \(w_0\in S^-\), write it as \(w_0 = \mkern 1.5mu\overline{\mkern-1.5muz_0\mkern-1.5mu}\mkern 1.5mu\), then \begin{align*} U(z_0) &\coloneqq-u(\mkern 1.5mu\overline{\mkern-1.5muz_0\mkern-1.5mu}\mkern 1.5mu) \\ &= {1\over 2\pi }\int_{-\pi}^\pi - u\qty{\mkern 1.5mu\overline{\mkern-1.5muz_0 + re^{it} \mkern-1.5mu}\mkern 1.5mu} \,dt\\ &= {1\over 2\pi }\int_{-\pi}^\pi - u\qty{\mkern 1.5mu\overline{\mkern-1.5muz_0\mkern-1.5mu}\mkern 1.5mu + re^{-it} } \,dt\\ &= {1\over 2\pi }\int_{-\pi}^\pi - u\qty{\mkern 1.5mu\overline{\mkern-1.5muz_0 + re^{-it} \mkern-1.5mu}\mkern 1.5mu} \,dt\\ &= {1\over 2\pi }\int_{-\pi}^\pi U(z_0 + re^{it} ) \,dt .\end{align*}
Reflection for the disc
-
State the standard Schwarz reflection principle involving reflection across the real axis.
-
Give a linear fractional transformation \(T\) mapping \({\mathbb{D}}\) to \({\mathbb{H}}\). Let \(g(z) = \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu\), and show \begin{align*} (T^{-1} \circ g \circ T)(z) = 1/\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu .\end{align*}
- Suppose that \(f\) is holomorphic on \({\mathbb{D}}\), continuous on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\), and real on \(S^1\). Show that \(f\) must be constant.
Part 1: Let \(\Omega = \Omega^+ \cup I \cup\Omega^-\) be a region symmetric about \({\mathbb{R}}\). If \(f\) is holomorphic on \(\Omega^+\) extending continuously to \(I\) and real valued on \(I\), then \(f\) extends to a holomorphic function \(F\) on all of \(\Omega\) defined on \(\Omega^-\) by \(F(z) = \mkern 1.5mu\overline{\mkern-1.5muf(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu\).
Part 2: The map is \(T(z) = -i\qty{z+1\over z-1}\) with \(T^{-1}(z) = {z-i\over z+i}\), so \begin{align*} (T^{-1}\circ g \circ T)(z) &= T^{-1}\mkern 1.5mu\overline{\mkern-1.5mu\qty{-i {z+1\over z-1} }\mkern-1.5mu}\mkern 1.5mu \\ &= T^{-1}\qty{i{\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu + 1 \over \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu - 1}} \\ &= {i\qty{\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu + 1 \over \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu - 1} - i \over i\qty{\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu + 1 \over \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu - 1} + i } \\ &= {(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu + 1) - (\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu - 1) \over (\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu + 1) + (\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu - 1)} \\ &= {1\over \mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu} .\end{align*}
Part 3: Define \(h: {\mathbb{H}}\to \mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{H}}\mkern-1.5mu}\mkern 1.5mu\) by \(h(z) = (T\circ f\circ T^{-1})(z)\). Under \(T^{-1}: {\mathbb{D}}\to {\mathbb{H}}\), we have \(T(S^1) = {\mathbb{R}}\), so \(h\) is a holomorphic function on \({\mathbb{H}}\) that is continuous and real-valued on \({\mathbb{R}}\). By the reflection principle, defining \(H(z) \coloneqq\mkern 1.5mu\overline{\mkern-1.5muh(\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu\) for \(\Im(z) < 0\) yields an entire function \(H: {\mathbb{C}}\to {\mathbb{C}}\) Noting that for \(g(z) \coloneqq\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu\), \(g=g^{-1}\), we can write \begin{align*} H \coloneqq g^{-1}\circ h \circ = h^{-1}\circ (T^{-1}\circ f \circ T)\circ g .\end{align*} We can then conjugate \(H\) by \(T\) to get a direct formula in terms of \(f\), and unwinding this yields the extension \(F:{\mathbb{C}}\to {\mathbb{C}}\) defined by \begin{align*} F(z) = \begin{cases} f(z) & z\in {\mathbb{D}} \\ f_-(z) \coloneqq{1\over \mkern 1.5mu\overline{\mkern-1.5muf\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu\mkern-1.5mu}\mkern 1.5mu} & z\in {\mathbb{D}}^c \\ f(z) = f_i(z) & z\in S^1 \end{cases} .\end{align*} In particular, \(H\) is an entire bounded function and thus constant, making \(F\) constant as well and consequently \(f\) is constant.
Spring 2020 HW 2, SS 2.6.15 (Constant on boundary and nonvanishing implies constant, using Schwarz)
Suppose \(f\) is continuous and nonvanishing on \(\mkern 1.5mu\overline{\mkern-1.5mu{\mathbb{D}}\mkern-1.5mu}\mkern 1.5mu\), and holomorphic in \({\mathbb{D}}\). Prove that if \({\left\lvert {z} \right\rvert} = 1 \implies {\left\lvert {f(z)} \right\rvert} = 1\), then \(f\) is constant.
Hint: Extend \(f\) to all of \({\mathbb{C}}\) by \(f(z) = 1/ \mkern 1.5mu\overline{\mkern-1.5muf(1/\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu\) for any \({\left\lvert {z} \right\rvert} > 1\), and argue as in the Schwarz reflection principle.
First, note that the Schwarz reflection principle can be applied here: let \(T: {\mathbb{D}}\to {\mathbb{H}}\) be the Cayley map, and consider \(\tilde f \coloneqq T\circ f \circ T^{-1}: {\mathbb{H}}\to {\mathbb{H}}\). Now \(T(S^1) = {\mathbb{R}}\), and since \(f(z)\in S^1\) when \(z\in S^1\), we have \(\tilde f({\mathbb{R}}) = {\mathbb{R}}\), i.e. this is a real-valued function on \({\mathbb{R}}\). So \(\tilde f\) extends holomorphically to \(\tilde F:{\mathbb{C}}\to CC\), and we can pull this back to a holomorphic extension of \(f\).
Extend \(f\) to \(F:{\mathbb{C}}\to {\mathbb{C}}\) by \(f(z) = 1/\mkern 1.5mu\overline{\mkern-1.5muf(1/\mkern 1.5mu\overline{\mkern-1.5muz\mkern-1.5mu}\mkern 1.5mu)\mkern-1.5mu}\mkern 1.5mu\) for \(z\in {\mathbb{D}}^c\), which generally has poles at the points \(1/\mkern 1.5mu\overline{\mkern-1.5muz_k\mkern-1.5mu}\mkern 1.5mu\) for \(z_k\in {\mathbb{D}}\) zeros of \(f\). Since \(f\) is nonvanishing, \(F\) has no poles and thus defines an entire function. By definition of \(F\), we have \(F({\mathbb{C}}) \subseteq f\qty{\left\{{{\left\lvert {z} \right\rvert} \leq 1}\right\}} \cup\mkern 1.5mu\overline{\mkern-1.5mu f\qty{\left\{{{\left\lvert {z} \right\rvert} \geq 1}\right\}}\mkern-1.5mu}\mkern 1.5mu\), which are both the continuous images of compact sets and thus compact and bounded. So \(F\) is a bounded entire function and thus constant.
Unsorted
Tie’s Extra Questions: Fall 2015
-
Let \(f(z) \in H({\mathbb D})\), \(\text{Re}(f(z)) >0\) and \(f(0)= a>0\). Show that \begin{align*} {\left\lvert { \frac{f(z)-a}{f(z)+a}} \right\rvert} \leq |z|, \; \; \; |f'(0)| \leq 2a .\end{align*}
-
Show that the above is still true if \(\text{Re}(f(z)) >0\) is replaced with \(\text{Re}(f(z)) \geq 0\).
Tie’s Extra Questions: Spring 2015
-
Let \(p(z)\) be a polynomial, \(R>0\) any positive number, and \(m \geq 1\) an integer. Let \(M_R = \sup \{ |z^{m} p(z) - 1|: |z| = R \}\). Show that \(M_R>1\).
-
Let \(m \geq 1\) be an integer and \(K = \{z \in {\mathbb C}: r \leq |z| \leq R \}\) where \(r<R\). Show (i) using (1) as well as, (ii) without using (1) that there exists a positive number \(\varepsilon_0>0\) such that for each polynomial \(p(z)\), \begin{align*}\sup \{|p(z) - z^{-m}|: z \in K \} \geq \varepsilon_0 \, .\end{align*}
Tie’s Extra Questions: Spring 2015
-
Explicitly write down an example of a non-zero analytic function in \(|z|<1\) which has infinitely zeros in \(|z|<1\).
-
Why does not the phenomenon in (1) contradict the uniqueness theorem?
Tie’s Extra Questions: Spring 2015
Let \(f\) be holomorphic in a neighborhood of \(D_r(z_0)\). Show that for any \(s<r\), there exists a constant \(c>0\) such that \begin{align*}||f||_{(\infty, s)} \leq c ||f||_{(1, r)},\end{align*} where \(\displaystyle |f||_{(\infty, s)} = \text{sup}_{z \in D_s(z_0)}|f(z)|\) and \(\displaystyle ||f||_{(1, r)} = \int_{D_r(z_0)} |f(z)|dx dy\).
Note: Exercise 3.8.20 on p.107 in Stein et al is a straightforward consequence of this stronger result using the integral form of the Cauchy-Schwarz inequality in real analysis.
Tie’s Extra Questions: Spring 2015
Let \(f\) be an analytic function on a region \(\Omega\). Show that \(f\) is a constant if there is a simple closed curve \(\gamma\) in \(\Omega\) such that its image \(f(\gamma)\) is contained in the real axis.
Tie’s Extra Questions: Spring 2015
-
Show that \(\displaystyle \frac{\pi^2}{\sin^2 \pi z}\) and \(\displaystyle g(z) = \sum_{n = - \infty}^{ \infty} \frac{1}{(z-n)^2}\) have the same principal part at each integer point.
-
Show that \(\displaystyle h(z) = \frac{\pi^2}{\sin^2 \pi z} - g(z)\) is bounded on \(\mathbb C\) and conclude that \(\displaystyle \frac{\pi^2}{\sin^2 \pi z} = \sum_{n = - \infty}^{ \infty} \frac{1}{(z-n)^2} \, .\)
Tie’s Extra Questions: Spring 2015
Assume \(f(z)\) is analytic in \({\mathbb D}: |z|<1\) and \(f(0)=0\) and is not a rotation (i.e. \(f(z) \neq e^{i \theta} z\)). Show that \(\displaystyle \sum_{n=1}^\infty f^{n}(z)\) converges uniformly to an analytic function on compact subsets of \({\mathbb D}\), where \(f^{n+1}(z) = f(f^{n}(z))\).
Tie’s Extra Questions: Spring 2015
Let \(f\) be a non-constant analytic function on \(\mathbb D\) with \(f(\mathbb D) \subseteq \mathbb D\). Use \(\psi_{a} (f(z))\) (where \(a=f(0)\), \(\displaystyle \psi_a(z) = \frac{a - z}{1 - \mkern 1.5mu\overline{\mkern-1.5mua\mkern-1.5mu}\mkern 1.5muz}\)) to prove that \(\displaystyle \frac{|f(0)| - |z|}{1 + |f(0)||z|} \leq |f(z)| \leq \frac{|f(0)| + |z|}{1 - |f(0)||z|}\).
Tie’s Extra Questions: Spring 2015
Let \(f\) be holomorphic in a neighborhood of \(D_r(z_0)\). Show that for any \(s<r\), there exists a constant \(c>0\) such that \begin{align*} \|f\|_{(\infty, s)} \leq c \|f\|_{(1, r)} ,\end{align*} where \(\displaystyle \|f\|_{(\infty, s)} = \text{sup}_{z \in D_s(z_0)}|f(z)|\) and \(\displaystyle \|f\|_{(1, r)} = \int_{D_r(z_0)} |f(z)|dx dy\).
Tie’s Extra Questions: Spring 2015
Let \(\Omega\) be a simply connected open set and let \(\gamma\) be a simple closed contour in \(\Omega\) and enclosing a bounded region \(U\) anticlockwise. Let \(f: \ \Omega \to {\mathbb C}\) be a holomorphic function and \(|f(z)|\leq M\) for all \(z\in \gamma\). Prove that \(|f(z)|\leq M\) for all \(z\in U\).
Tie’s Extra Questions: Spring 2015
Let \(f\) be holomorphic in a neighborhood of \(D_r(z_0)\). Show that for any \(s<r\), there exists a constant \(c>0\) such that \begin{align*}\|f\|_{(\infty, s)} \leq c \|f\|_{(1, r)},\end{align*} where \(\displaystyle \|f\|_{(\infty, s)} = \text{sup}_{z \in D_s(z_0)}|f(z)|\) and \(\displaystyle \|f\|_{(1, r)} = \int_{D_r(z_0)} |f(z)|dx dy\).
Tie’s Extra Questions: Fall 2016
-
\(f(z)= u(x,y) +i v(x,y)\) be analytic in a domain \(D\subset {\mathbb C}\). Let \(z_0=(x_0,y_0)\) be a point in \(D\) which is in the intersection of the curves \(u(x,y)= c_1\) and \(v(x,y)=c_2\), where \(c_1\) and \(c_2\) are constants. Suppose that \(f'(z_0)\neq 0\). Prove that the lines tangent to these curves at \(z_0\) are perpendicular.
-
Let \(f(z)=z^2\) be defined in \({\mathbb{C}}\).
-
Describe the level curves of \(\mbox{\textrm Re}{(f)}\) and of \(\mbox{Im}{(f)}\).
-
What are the angles of intersections between the level curves \(\mbox{\textrm Re}{(f)}=0\) and \(\mbox{\textrm Im}{(f)}\)? Is your answer in agreement with part a) of this question?
Tie’s Extra Questions: Fall 2016
-
\(f: D\rightarrow {\mathbb C}\) be a continuous function, where \(D\subset {\mathbb C}\) is a domain.Let \(\alpha:[a,b]\rightarrow D\) be a smooth curve. Give a precise definition of the complex line integral \begin{align*}\int_{\alpha} f.\end{align*}
-
Assume that there exists a constant \(M\) such that \(|f(\tau)|\leq M\) for all \(\tau\in \mbox{\textrm Image}(\alpha\)). Prove that \begin{align*}\big | \int_{\alpha} f \big |\leq M \times \mbox{\textrm length}(\alpha).\end{align*}
- Let \(C_R\) be the circle \(|z|=R\), described in the counterclockwise direction, where \(R>1\). Provide an upper bound for \(\big | \int_{C_R} \dfrac{\log{(z)} }{z^2} \big |,\) which depends only on \(R\) and other constants.
Tie’s Extra Questions: Fall 2016
- Let \(F\) be an analytic function inside and on a simple closed curve \(C\), except for a pole of order \(m\geq 1\) at \(z=a\) inside \(C\). Prove that
\begin{align*}\frac{1}{2 \pi i}\oint_{C} F(\tau) d\tau = \lim_{\tau\rightarrow a} \frac{d^{m-1}}{d\tau^{m-1}}\big((\tau-a)^m F(\tau))\big).\end{align*}
- Evaluate \begin{align*}\oint_{C}\frac{e^{\tau}}{(\tau^2+\pi^2)^2}d\tau\end{align*} where \(C\) is the circle \(|z|=4\).
Tie’s Extra Questions: Spring 2014, Fall 2009, Fall 2011
For \(s>0\), the gamma function is defined by \(\displaystyle{\Gamma(s)=\int_0^{\infty} e^{-t}t^{s-1} dt}\).
-
Show that the gamma function is analytic in the half-plane \(\Re (s)>0\), and is still given there by the integral formula above.
-
Apply the formula in the previous question to show that \begin{align*} \Gamma(s)\Gamma(1-s)=\frac{\pi}{\sin \pi s} .\end{align*}
Hint: You may need \(\displaystyle{\Gamma(1-s)=t \int_0^{\infty}e^{-vt}(vt)^{-s} dv}\) for \(t>0\).
Tie’s Extra Questions: Fall 2011
\envlist
-
Show that the function \(u=u(x,y)\) given by \begin{align*}u(x,y)=\frac{e^{ny}-e^{-ny}}{2n^2}\sin nx\quad \text{for}\ n\in {\mathbf N}\end{align*} is the solution on \(D=\{(x,y)\ | x^2+y^2<1\}\) of the Cauchy problem for the Laplace equation \begin{align*}\frac{\partial ^2u}{\partial x^2}+\frac{\partial ^2u}{\partial y^2}=0,\quad u(x,0)=0,\quad \frac{\partial u}{\partial y}(x,0)=\frac{\sin nx}{n}.\end{align*}
-
Show that there exist points \((x,y)\in D\) such that \(\displaystyle{\limsup_{n\to\infty} |u(x,y)|=\infty}\).